Lateral prefrontal cortex contributes to maladaptive decisions

Abstract

Humans consistently make suboptimal decisions involving random events, yet the underlying neural mechanisms remain elusive. Using functional MRI and a matching pennies game that captured subjects’ increasing tendency to predict the break of a streak as it continued [i.e., the “gambler's fallacy” (GF)], we found that a strong blood oxygen level-dependent response in the left lateral prefrontal cortex (LPFC) to the current outcome preceded the use of the GF strategy 10 s later. Furthermore, anodal transcranial direct current stimulation over the left LPFC, which enhances neuronal firing rates and cerebral excitability, increased the use of the GF strategy, and made the decisions more “sticky.” These results reveal a causal role of the LPFC in implementing suboptimal decision strategy guided by false world models, especially when such strategy requires great resources for cognitive control.

The ability to perceive patterns and to use them to guide decisions is an important aspect of human cognition. During the long history of evolution, the human brain has been well adapted to the statistical regularities in the environment (1, 2). Nevertheless, humans have been consistently shown to be bad at making decisions involving “independently and identically distributed” random events generated by the Bernoulli process, exhibiting suboptimal behaviors such as probability matching and the “gambler's fallacy” (GF) (3–5). In particular, the GF is an increasing tendency to predict the break of a streak generated by a random process (e.g., flipping a fair coin) when the streak gets longer (6), and has been observed in many laboratory and real-life situations (6–9).

Behavioral research has suggested that the GF is a cognitive bias generated by a false perception of the random process (e.g., the small number law) (6, 10), which is probably formed through years of evolution in response to the pattern-rich world (1, 2). Consistently, the subjective beliefs about the specific generating mechanisms (i.e., the world model) could significantly affect participants’ predictions (6–9). Computational models show that a rational mind guided by a false “world model” (i.e., outcome dependency) could well generate this type of suboptimal decisions, which can be changed by alternations of the world model (11). Nevertheless, the neural mechanisms of the GF have not been clearly addressed.

Several lines of research have suggested the involvement of the prefrontal cortex (PFC) in several decision processes that could contribute to the GF strategy. First, the PFC is good at detecting and constructing patterns, especially out of randomness (12). Second, the PFC plays an important role in decision making by encoding a particular state of the environment and the desirability of the outcome expected from such a state (13, 14). During the pennies-matching gamble, PFC neurons have been shown to encode multiple types of information related to decision making (including animals’ past decisions, payoffs, and their conjunction), suggesting its role in updating the animal's decision-making strategy as well as determining the animal's choice in a given trial (15, 16). Consistently, functional imaging studies also showed that the PFC is involved in probability matching behavior (17). Anodal transcranial direct current stimulation (tDCS) over the left PFC has led to faster probability matching strategies and slower maximizing strategies (18). Finally, a recent study shows that the GF-like decision (e.g., more risk-taking behavior after losses than after wins) was correlated with the activation of the left PFC (19). Nevertheless, the exact role of the PFC (e.g., working memory, novelty detection, or decision-making) in these tasks is not clear (20), and a causal relationship between activities in the PFC and the use of the GF strategy is yet to be established. We addressed these questions by using a combination of functional MRI (fMRI) and tDCS technologies. In particular, we tested whether activities in the PFC can predict the use of the GF strategy, and whether tDCS over the PFC can alter the use of this strategy.

Results

Behavioral Results.

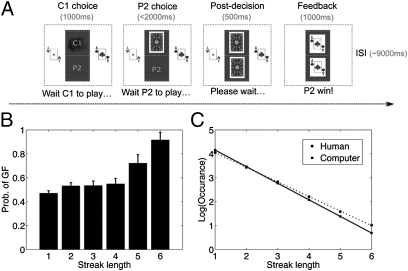
We used a pennies-matching gamble implemented in a card-guessing task (Fig. 1A). Subjects (P2) were asked to predict the computer's (C1) choice of a black or red card. The computer's choices followed a predetermined, canonical random sequence generated by a Bernoulli process characterized by (i) equal numbers of black and red cards, (ii) switch of card choice on half the trials (Fig. S1), and (iii) streak length in an exponential distribution (Fig. 1C). The procedure guarantees that at any streak length, the probability that a streak will continue or break is 50%. The optimal strategy (i.e., Nash equilibrium) is to predict the computer's choice randomly. Nevertheless, previous studies showed that neither monkeys (15, 16) nor human subjects (21) played according to this strategy, and were thus beaten by a computer opponent that was able to detect the patterns in their choices.

Fig. 1.

Experimental paradigm and behavioral results in the fMRI study. Subjects were asked to guess the computer's choice of black or red card. Not shown here, the computer's most recent five choices were shown on the top of the computer screen to reduce working memory load. (B) Behavioral results: bar graph shows the percentage of using the GF strategy in the next trial as a function of the length of streak computer made. The GF was defined as the strategy to not follow the computer's most recent choice, which increased monotonically with streak length. (C) The number of short and long streaks subjects made in their choice. The log of occurrence against streak length was fitted by a linear function.

A subject using the GF strategy would predict that the computer's choice is more likely to switch in the next trial when the streak gets longer. Thus, the GF is defined as a strategy to deviate from the computer's last choice, which can be used under both short and long streaks. This is in contrast to the win–stay, lose–shift (WSLS) strategy in stochastic decision-making, which refers to the strategy to follow the computer's last choice (15, 16). Although this definition of WSLS is different from its traditional definition, the two definitions are essentially equivalent. That is, with this strategy, if the player's choice matches the computer's choice in this trial (i.e., win), he or she will stick to this (also the computer's) choice in the next trial (i.e., stay); otherwise (i.e., loss), he or she will switch (i.e., shift) to the other choice, which is the computer's current choice.

Consistent with previous observations (6–9), subjects’ use of the GF strategy increased with streak length [F(5,85) = 15.46, P < 0.001; Fig. 1B]. They also exhibited probability matching behavior, choosing both cards with equal probability [t(17) = 0.18, P = 0.86; Fig. S1A]. However, they switched significantly less often than the computer [44.8% vs. 50%, t(17) = −2.74, P = 0.01; Fig. S1B]. In other words, their choices contained longer streaks than that generated by the canonical random process used by the computer (Fig. 1C), although they predicted that a long streak was more likely to break in a random sequence. Interestingly, when subjects were asked to write down a random sequence, they were less likely to generate a long streak (1, 5).

For a predetermined sequence with a given length, a long streak of a particular card would increase its local cumulative probability, which should be eventually reduced in a long run. As a result, it would be rational to track the cumulative probability and use that to guide decisions. It is thus important to separate the two strategies [the one relying on the streak length, (i.e., the GF, and the one relying on the cumulative probability)] because they both lead to the same decision. In our study, we carefully selected sequences in which the streak length was not correlated with the cumulative probability (r = 0.12, P = 0.18). The use of the GF strategy would be obvious if subjects increasingly kept away from the computer's most recent choice with longer streaks even after controlling for the effect of cumulative probability. To examine this issue, a lagged logistic regression analysis was conducted by using subjects’ next strategy [keeping away from (value 1) vs. following (value 0) the computer's current choice] as the dependent measure, and streak length (i.e., 1–6), current outcome [win (i.e., 1) vs. loss (i.e., −1)], their interaction, and the cumulative probability of the current card as independent measures. This analysis still revealed significant effect of streak length (β = 0.18, t = 4.69, P < 0.001), suggesting that subjects used the GF strategy more often as the streak gets longer, although cumulative probability also had a significant impact on subjects’ decisions (β = 2.64, t = 5.42, P < 0.001). However, we found no effect of current outcome (β = 0.11, t = 1.34, P = 0.18). Using this model on each individual subject, we could on average correctly predict 62.4% of subjects’ choices (t = 9.00, P < 0.0001).

Subjects’ response times were not affected by the outcome from the previous trial [win vs. loss: t(17) = 0.84, P = 0.41], subjects’ current choices [switch vs. stay: t(17) = 1.34, P = 0.20], subjects’ current strategy [GF vs. WSLS: t(17) = 0.28, P = 0.78], or streak length [F(5,85) = 0.9, P = 0.48]. It should be noted switches of card choices were decoupled from switches of motor responses because the positions of the red and black cards were randomly switched from trial to trial.

fMRI Results: Left PFC Activity Preceded Use of GF Strategy.

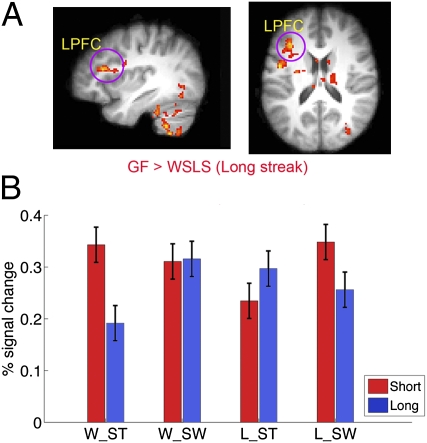
We used fMRI to examine the neural activities that could predict the use of the GF strategy. To this end, we focused on the neural responses in the feedback stage and examined whether the activations could predict subjects’ next choice (switch vs. stay) and/or their strategy in the next choice (GF vs. WSLS), and how it was modulated by streak length, as suggested by the behavioral data. Trials were categorized according to streak length (short vs. long), outcome (win vs. loss), and subjects’ next choice (stay vs. switch), and the cumulative probability of the current card was added as a covariate of no interest. We found no significant activation at the whole brain level that was predictive of subjects’ next choice (switch vs. stay) approximately 10 s later. In contrast, the blood oxygen level-dependent responses in several regions could predict subjects’ strategy, which was modulated by streak length. In particular, in the long streak condition in which the GF strategy was dominant, stronger activation in the left lateral PFC [LPFC; x/y/z values in the Montreal Neurological Institute (MNI) coordinate system of −36, 26, and 18; Z = 3.76] preceded the use of the GF strategy in the next trial (Fig. 2A). Other regions that showed the same response profile included the left middle/inferior temporal gyrus, right thalamus, and cerebellum (Table S1). The left LPFC region was not involved in the GF strategy under short streaks, but showed a trend toward WSLS strategy [F(1,17) = 3.65, P = 0.07], and there was a significant three-way interaction [F(1,17) = 10.43, P = 0.005]. Whole-brain analysis of three-way interaction also revealed an overlapping cluster in this region (MNI coordinates of −34, 24, and 22; Z = 4.08; Fig. S2), providing strong evidence that the LFPC was specifically involved in the GF strategy under long streaks. The left LPFC was not sensitive to gains or losses [F(1,17) = 0.05, P = 0.82; Fig. 2B].

Fig. 2.

Activity of LPFC predicted the GF strategy under long streaks. A stronger activation to feedback in the LPFC preceded a GF strategy in the next trial. The results (i.e., GF > WSLS) are overlaid on the (A) sagittal and axial slices of the group mean structural image. All activations were thresholded by using cluster detection statistics, with a height threshold of z > 2.3 and a cluster probability of P < 0.05, corrected for whole-brain multiple comparisons. (B) Plots of percentage signal change in left LPFC shows that it was specifically involved in the GF under a long streak, and was not sensitive to reward. Error bars denote within-subject error.

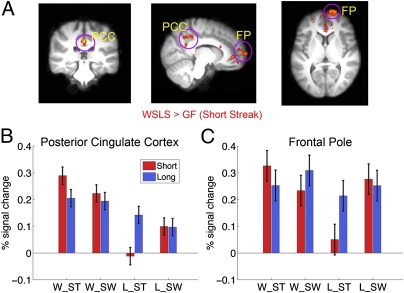
In the short streak condition, stronger activations in the frontal pole (FP; MNI coordinates of 12, 72, and 6; Z = 3.35) and posterior cingulate cortex (PCC; MNI coordinates of 0, −30, and 36; Z = 3.92) preceded the use of the WSLS strategy in the next trial (Fig. 3A). Further analysis indicated that this result was primarily driven by the observation that a strong response to the current loss was associated with switching to an alternative choice in the next trial [FP, t(17) = 2.62, P = 0.018; PCC, t(17) = 1.99, P = 0.06], but no difference was found under the win condition (P > 0.16; Fig. 3 B and C).

Fig. 3.

FP and PCC encoded the value of alternative options under short streaks. The results (i.e., WSLS > GF) are overlaid on the (A) coronal, sagittal, and axial slices of the group mean structural image. All activations were thresholded by using cluster detection statistics, with a height threshold of z > 2.3 and a cluster probability of P < 0.05, corrected for whole-brain multiple comparisons. B and C show the percentage signal change for the PF and PCC ROIs, respectively, which suggest that this result was primarily driven by a stronger response to loss when subjects were to switch to alternative choice in the next trial. Error bars denote within-subject error.

In addition, a wide network of cortical areas showed stronger activations to gains than to losses (Fig. S3). Focusing on the three regions that has been implicated in reward processing (22, 23), including the ventral medial PFC (VMPFC; MNI coordinates of −4, 48, and −8; Z = 5.40), left (MNI coordinates of −6, 10, −10; Z = 5.57) and right (MNI coordinates of 8, 8, and −8; Z = 5.58) ventral striatum, we found that activations in these regions simply coded the outcome, but not subjects’ next choice or strategy. In addition, the reward signal in the VMPFC was reduced under long streaks [streak-by-outcome interaction: [F(1,17) = 9.84, P = 0.006]).

tDCS Results: Anodal Stimulation of Left LPFC Increased GF.

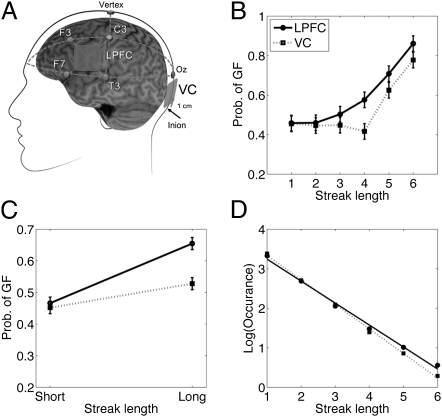
To further identify the causal relationship between the left LPFC and the GF strategy, a tDCS study was conducted on a separate group of 18 college students. Anodal tDCS has been shown to increase neuronal firing rates and thus enhance cerebral excitability, whereas effects of cathodal tDCS are less stable (24). Based on the fMRI results, we predicted that anodal tDCS over the left LPFC, compared with the control site [i.e., visual cortex (VC); Fig. 4A], would enhance the use of the GF strategy, in particular under long streaks.

Fig. 4.

Anodal tDCS over the LPFC, compared with the VC, increased the use of the GF strategy. (A) Schematic representation of the locations of the tDCS. (B) Percentage of using the GF strategy as a function of tDCS site and streak length. (C) The same result is plotted again by dividing the streaks into short streaks (≤3) and long streaks (≥4), revealing a clear streak length–by–stimulation site interaction. (D) The number of short and long streaks subjects made in their choices as a function of tDCS. The legend to Fig. 1 provides further details. Error bars represent within-subject error.

Our data supported this hypothesis. Consistent with the fMRI study, the use of the GF strategy increased with streak length [F(5,85) = 18.32, P < 0.0001; Fig. 4B]. More importantly, we found a significant streak length–by–tDCS interaction [F(1,17) = 8.67, P = 0.009; Fig. 4C]. Additional planned post-hoc t tests indicated that LPFC stimulation significantly increased the GF strategy under long streaks [t(17) = 4.03, P = 0.008], but had no effect under short streaks (P = 0.74). The tDCS effect was most robust under streak 4, although the size of the effect was not statistically different from those under streaks 5 and 6 [F(2,34) = 0.38, P = 0.68]. LPFC stimulation also increased the stickiness of the choices (i.e., subjects committed more long streaks but fewer short streaks in their choices) as indicated by the marginally significant streak by site interaction [F(1,17) =3.74, P = 0.07; Fig. 4D]. Under both conditions, subjects switched less than 50% (43% and 46%; P = 0.007 and P = 0.04), and there was a slight trend that subjects switched less often after LPFC stimulation than after VC stimulation [t(17) = 1.51, P = 0.15].

A similar lagged logistic regression analysis was used to control the effect of cumulative probability, with the stimulation site [LPFC (value of 1) vs. VC (value of −1)] and its interaction with streak length as additional variables. Consistent with the behavioral data in the fMRI study, this analysis revealed significant effects of streak length (β = 0.034, t = 5.51, P < 0.001), cumulative probability (β = 0.147, t = 2.03, P = 0.04), but no effect of current outcome (β = 0.005, t = 0.37, P = 0.72). More importantly, we found a significant effect of stimulation site–by–streak length interaction (β = 0.008, t = 2.42, P = 0.016), indicating that LPFC stimulation increased the GF under long streaks, even after controlling the effect of cumulative probability. Nevertheless, tDCS did not change subjects’ preference for black or red cards [t(17) = 0.61, P = 0.55].

Previous studies have shown that training significantly reduced the GF (18, 25), probably by updating the world model. To reduce practice effects, the two sessions were administered at least 7 d apart. As a result, we only found a small trend of practice effect across the two test sessions [F(1,17) = 2.38, P = 0.14; Fig. S4]. To exclude any possible stimulation site–by–practice interaction, we performed an additional between-subject t test using the data from the first session, in which half the subjects were under LPFC stimulation and the other half were under VC stimulation. With only nine subjects in each group, we still found a significant tDCS effect [F(1,32) = 5.1, P = 0.03], and a marginally significant stimulation–by–streak length interaction [F(1,32) = 2.29, P = 0.14]. A further t test revealed a strong tDCS effect under long streaks [t(16) = 2.33, P = 0.03], but no effect under short streaks [t(16) = 0.64, P = 0.53; Fig. S5].

Discussion

The role of the LPFC in suboptimal decision-making involving random events was investigated by a combination of fMRI and tDCS techniques. We found that subjects showed increased tendency to use the GF strategy when the streak continued, which was predicted by activations of the left LPFC approximately 10 s before the decision was made. Anodal stimulation using tDCS over the left LPFC, which has been shown to increase cerebral excitability (18, 24), increased the use of the GF strategy. These results established a causal relationship between activities of the left LPFC and the implementation of suboptimal decision strategies such as the GF.

The LPFC plays several important roles in decision-making that may contribute to decision biases involving random events, including short-term memory, pattern detection and construction (20), and integration of contextual information to guide decisions (13). In addition to these critical functions, our results suggest that the LPFC plays a unique role in implementing decisions guided by the world model, especially when such implementation requires conflict resolution. In contrast to the WSLS strategy that is likely guided by a model-free, reinforcement learning mechanism, the GF strategy represents a case in which subjects showed a Win-Shift, Loss-Stay pattern. As shown by many computational and behavioral studies, this counterintuitive behavior might be guided by a false world model that posits dependency in outcomes that are in fact random (6–11, 26). To implement this decision thus requires subjects to hold the prepotent WSLS response and switch to the opposite response. The strong activation that preceded the GF strategy is thus in concordance with the role of the LPFC in conflict resolution (27) and set switches (28, 29). The LPFC is also involved in expressing the new behavior under the prolonged interference of the old behavior (30). This is also consistent with recent behavioral data showing that a longer intertrial interval (6 s vs. 2 s) increased the use of the GF strategy, contradicting the traditional heuristic account (31). This result could not be attributed to short-term memory or pattern detection, because they were matched in our experiments independent of the strategy (WSLS vs. GF) subjects used. Moreover, the requirement for short-term memory and pattern detection was greatly minimized in this experiment by presenting the computer's most recent five choices on the screen.

A salient pattern of FP and PCC responses is that a strong response to the current loss was associated with switching to the other card in the next trial. Other than that, they overall showed very little sensitivity to the current outcome. The characteristics of the FP response are in contrast to the activations in the VMPFC that primarily track the current reward value (22, 23). This is quite consistent with human functional imaging studies showing that, whereas the VMPFC tracks the current reward, the FP and PCC track the reward probability of the unchosen option (i.e., counterfactual prediction error) (32) and the potential value of switching to alternative actions (33). This observation is also in agreement with the animal literature showing that the FP (34, 35) and PCC (36, 37) are involved in monitoring and evaluating self-generated decisions and deciding on when to switch to an alternative option for a better outcome. Taken together, our results suggest a triple dissociation of PFC in decision-making: the LPFC in implementing the decision guided by a world model, the FP in computing the value of alternative options especially when a loss is experienced, and the VMPFC in tracking the current reward value. The triple dissociation provides additional evidence to suggest that the PFC contains multiple mechanisms for decision making (38).

Cumulative evidence has shown that human decisions are guided by multiple mechanisms, including, but not limited to, a model-free, reinforcement learning mechanism that guides exploitation and a “model-based” mechanism that guides exploration (39, 40). It has been argued that this model-based decision-making mechanism might well contribute to the observed decision biases involving random events, such as probability matching (11). At the neural level, distinct neural systems are involved in the two mechanisms (40, 41), and recent evidence suggests a more integrated computational architecture of the two systems (42). Model-based decision plays an important role under complex situations in which contingency is not readily apparent to the subjects (e.g., tree search) (41). Consistently, our result suggests that, for decision under maximum uncertainty in which there is no consistent stimulus–reward contingency (reward probability for either option is 50%), the decisions are more guided by the part of PFC that is involved in model-based decision, such as the LPFC, rather than the model-free regions, such as the VMPFC and striatum. Strikingly, under long streaks, the reward signal in the VMPFC was reduced. Presumably, the diminished reward signal under long streaks would also facilitate the implementation of the GF strategy. This is consistent with the observation that patients with damage in the VMPFC were more likely to engaged in the GF strategy (43, 44). Future studies are required to understand the interaction of the two decision mechanisms.

The fMRI-guided tDCS stimulation results provide support for the hypothesis that anodal stimulation facilitated the use of the GF strategy by enhancing the left LPFC function. They also provide additional evidence that tDCS could noninvasively modulate participants’ decision strategy (18, 45, 46). It has been shown that the left LPFC anodal/right LPFC cathodal DC stimulation reduced risk-taking behaviors (45, 46), and caused subjects to be faster in using the maximizing strategy in a probabilistic guessing task (18). Partly consistent with these results, we found that left LPFC anodal stimulation, compared with VC stimulation, increased the use of the GF strategy, especially under long streaks in which the use of the GF strategy starts to increase significantly. Although the effect was not significantly diminished at streaks 5 and 6, the smaller effect could be a result of the ceiling effect and measurement errors caused by smaller number of observations under longer streaks. Presumably, the tDCS effect could be stronger under other conditions when subjects are less likely to use the GF strategy, such as under short intertrial intervals (31). This remains to be examined in future studies. Still, by combining tDCS and fMRI, future studies can elucidate how tDCS stimulation affects the dynamic interactions of multiple decision systems and lead to changes in decision strategies.

In summary, although the LPFC is essential for goal-directed, flexible decision-making, our data suggest that this region also contributes to suboptimal decisions involving random events. In particular, the LPFC might play an important role in implementing decisions guided by a world model, real or false. The findings provide a unique perspective on the role of LPFC in rational and irrational decision-making.

Experimental Procedures

Subjects.

Eighteen healthy adults (11 men; mean age, 21.6 y) participated in the fMRI study, and another 18 subjects (nine men; mean age, 23 y) participated in the tDCS study. All subjects were free of neurological or psychiatric history. Informed written consent was obtained from the subjects before the experiments. The fMRI study was approved by the institutional review board of the National Key Laboratory of Cognitive Neuroscience and Learning at Beijing Normal University in China, and the tDCS study was approved by the local ethical committee at the National Central University in Taiwan.

Experimental Paradigm.

Subjects were asked to guess the computer's choice of red or black cards to win money (Fig. 1A). They won one Chinese Yuan or the equivalent in New Taiwan Dollars (4 dollars) each time they guessed correctly but otherwise lost one Yuan or 4 New Taiwan Dollars. They were told explicitly that the computer chose the card randomly. Each trial lasted 13 s: first, two cards (red and black) were presented on the left and right sides of the screen, respectively. The position of the red or black card varied randomly from trial to trial to dissociate decision switch from motor switch. The computer (C1) made the choice after 1 s. The subjects (P2) were then asked to make a guess within 2 s. One half second after the subjects’ choice, both the computer and subjects’ choices were revealed, and feedback was delivered for 1 s. The next trial started approximately 9 s later. To reduce short-term memory load, the computer's most recent five choices were presented on the top of the screen. There were 63 trials in each 13-min run.

fMRI Procedure.

Imaging data were acquired on a 3.0 T Siemens MRI scanner in the MRI Center at Beijing Normal University. A single-shot T2*-weighted gradient-echo echoplanar imaging sequence was used for functional imaging acquisition with the following parameters: repetition/echo times, 2,000 ms/30 ms; θ, 90°, field of view, 200 × 200 mm; matrix, 64 × 64; and slice thickness, 4 mm. Thirty contiguous axial slices parallel to the anterior/posterior commissure line were obtained to cover the whole cerebrum and partial cerebellum. Anatomical MRI data were acquired by using a T1-weighted, 3D, gradient-echo pulse-sequence (MPRAGE). The parameters for this sequence were as follows: repetition/echo times, 2,530 ms/3.39 ms; θ, 7°; field of view, 256 × 256 mm; matrix, 192 × 256; and slice thickness, 1.33 mm. One hundred twenty-eight sagittal slices were acquired to provide high-resolution structural images of the whole brain.

tDCS Procedure.

tDCS was delivered with a Magstim Eldith DC stimulator and a pair of electrodes housed in 4 × 4 cm saline solution-soaked sponge coverings. The center of the stimulation electrode was placed over the left LPFC, which was localized using the EEG 10–20 system, with the center of the tDCS electrode placed over the intersection of the F3–T3 line and the F7–C3 line (Fig. 4). For the control condition, the electrode was placed over the VC. The accuracy of this localization method was confirmed in six subjects by using an MRI-guided frameless stereotaxy system (Brainsight; Rogue Research). The reference electrode was placed over the left cheek of the subject. In the tDCS conditions the current was applied for 10 min with an intensity of 1.5 mA, or 0.0937 mA/cm². The total charge in our current experiment was 0.0056 C/cm². Both are far lower than the safety criterion according to Nitsche et al. (47), which suggested 25 mA/cm² for densities and 216 C/cm² for total charge. The LPFC and VC conditions were fully counterbalanced across subjects. The interval between the two conditions was least at 7 d to reduce the learning effect.

Lagged Logistic Regression Analysis of Behavioral Data.

We did a lagged logistic regression analysis to examine the effect of previous outcome (i.e., gain vs. loss), streak length (i.e., 1–6), their interaction, and the cumulative probability of the current card on subjects’ next strategy (i.e., GF vs. WSLS). In the overall logistic regression model, participant-specific dummies (e.g., dummy 1, coded as 1 for participant 1, 0 otherwise; dummy 2, coded as 1 for participant 2, 0 otherwise, and so on) were added. We also used this model to predict each individual's choice. The accuracy of the model was determined by using the following equation:

where f(x) represents the regression function and y is the model prediction.

A similar lagged regression was conducted on the tDCS data to control the effect of cumulative probability. tDCS site [LPFC (value of 1) vs. VC (value of −1)] and its interaction with streak length were included as additional regressors.

fMRI Data Analysis.

Image preprocessing and statistical analysis were carried out by using the FMRI Expert Analysis Tool (version 5.98; part of the FSL package; FMRIB software library, version 4.1; www.fmrib.ox.ac.uk/fsl). The first four volumes before the task were automatically discarded by the scanner to allow for T1 equilibrium. The remaining images were then realigned to correct for head movements (48). Translational movement parameters never exceeded one voxel in any direction for any subject or session. Data were spatially smoothed by using a 5-mm full width at half maximum Gaussian kernel, and filtered in the temporal domain by using a nonlinear high-pass filter with a 100-s cutoff. All images were denoised by using MELODIC independent-components analysis within FSL (49). EPI images were registered to the MPRAGE structural image, and into standard (i.e., MNI) space, by using affine transformations (48). Registration from MPRAGE structural image to standard space was further refined by using FNIRT nonlinear registration (50).

The data were modeled at the first level by using a general linear model within FSL's FILM module. The analysis focused on the feedback response and the goal was to use that activation to predict subjects’ next choice in 10 s. A full factorial design was used, which included the following three factors: streak length (short vs. long), current outcome (win vs. loss), and subjects’ next choice (switch vs. stay). The event onsets were convolved with the canonical hemodynamic response function (double-γ) to generate the regressors used in the GLM. Temporal derivatives were included as covariates of no interest to improve statistical sensitivity.

A higher-level analysis created cross-run contrasts for each subject for a set of contrast images by using a fixed-effect model. These were then input into a random-effect model for group analysis by using ordinary least squares simple mixed-effect with automatic outlier detection (51). Group images were thresholded by using cluster detection statistics, with a height threshold z of more than 2.3 and a cluster probability of P < 0.05, corrected for whole-brain multiple comparisons by using Gaussian random-field theory.

Region-of-Interest Analyses.

To explore the complex interactions in these regions identified by whole brain analysis, regions of interest (ROIs) were created by drawing a 3-mm sphere around the local maxima of the activation. For each subject, parameter estimates (i.e., β values) of each event type from the fitted model were extracted and averaged across all voxels in each ROI. Percent signal changes were calculated by multiplying [β/mean] by ppheight by 100%, where ppheight is the peak height of the hemodynamic response versus the baseline level of activity (which is determined by the event length and the convolved hemodynamic response function), and the mean is the average blood oxygen level-dependent signal of that ROI over time. Full details regarding percentage signal change calculation can be found in the online guideline by Jeanette Mumford (http://mumford.bol.ucla.edu/perchange_guide.pdf).