Skip to main content
PMC home page
Journal of Studies on Alcohol and Drugs logoLink to Journal of Studies on Alcohol and Drugs
. 2012 May;73(3):341–350. doi: 10.15288/jsad.2012.73.341

Alcohol-Related Risk of Driver Fatalities: An Update Using 2007 Data

Robert B Voas a, Pedro Torres a, Eduardo Romano a,*, John H Lacey a
PMCID: PMC3316710  PMID: 22456239

Abstract

Objective:

The purpose of this study was to determine whether the relative risk of being involved in an alcohol-related crash has changed over the decade from 1996 to 2007, a period during which there has been little evidence of a reduction in the percentage of all fatal crashes involving alcohol.

Method:

We compared blood-alcohol information for the 2006 and 2007 crash cases (N = 6,863, 22.8% of them women) drawn from the U.S. Fatality Analysis Reporting System (FARS) with control blood-alcohol data from participants in the 2007 U.S. National Roadside Survey (N = 6,823). Risk estimates were computed and compared with those previously obtained from the 1996 FARS and roadside survey data.

Results:

Although the adult relative risk of being involved in a fatal alcohol-related crash apparently did not change from 1996 to 2007, the risk for involvement in an alcohol-related crash for underage women has increased to the point where it has become the same as that for underage men. Further, the risk that sober underage men will become involved in a fatal crash has doubled over the 1996–2007 period.

Conclusions:

Compared with estimates obtained from a decade earlier, young women in this study are at an increased risk of involvement in alcohol-related crashes. Similarly, underage sober drivers in this study are more at risk of involvement in a crash than they were a decade earlier.

Overwhelming evidence from laboratory research performed with dosed subjects shows that alcohol consumption impairs driving skills (Moskowitz and Robinson, 1987; National Institute on Alcohol Abuse and Alcoholism, 1997). These laboratory findings have been tested with field data, which have been used to compare the blood alcohol concentration (BAC) of crash-involved drivers with that of non-crash-involved drivers to determine the relative risk (RR) of crash involvement as the driver’s BAC rises from .00%. Three of the most relevant research efforts are the Grand Rapids study (Borkenstein et al., 1964), its 1998–1999 replication in two U.S. cities by Blomberg et al. (2005), and the RR estimates provided by Zador (1991) and Zador et al. (2000) based on their linking of the 1996 National Roadside Survey (NRS; a quasi-decennial effort sponsored by the National Highway Traffic Safety Administration [NHTSA] and others) and the Fatality Analysis Reporting System (FARS; a census of all fatal crashes in the United States). These RR studies have provided lawmakers with a scientific basis for the design and implementation of several alcohol-related traffic safety policies, programs, and laws. Per se laws (initially at a BAC of .10, now .08) and zero-tolerance laws for underage drivers are examples of laws developed and adopted by all states based on data from RR studies.

The enactment of these scientifically based laws has been shown to be effective in reducing alcohol-related crash fatalities (Chen et al., 2006; Fell and Voas, 2006; Shults et al., 2001; Voas et al., 2003). Although the existing laws continue to restrain the number of alcohol-related crashes, after 15 years (1980–1995) of significant decline (from 69% to 41% of all fatal crashes), impaired-driving fatalities are no longer declining in the United States. It has been suggested that risk-taking attitudes might have changed over the last decade, making some groups of drivers unexpectedly vulnerable to crashes (Romano et al., 2009). The existing battery of laws and policies might be failing to accommodate such changes in risk-taking attitudes. It is therefore apparent that alcohol-related RR crash estimates need to be updated. Unfortunately, obtaining these estimates is never straightforward, and collecting the required field data involves considerable expense. However, the results of the Zador et al. (2000) risk analysis on the 1996 NRS survey data have provided a method of determining whether driving attitudes and practices have changed. By linking the 2007 NRS data to the FARS, we produced updated BAC RR estimates for different demographic groups and drinking statuses for 2007 weekend nighttime drivers to compare with the risk levels for 1996 reported by Zador et al. (2000). In summary, we aim in this study to estimate the BAC RR (i.e., crash risk at different BAC levels relative to .00%) for drivers of varying ages and genders exposed to different driving situations (i.e., single-vehicle or multiple-vehicle crashes).

Method

Data

Crash exposure.

Measures of crash exposure were obtained from the 2007 NRS (Lacey et al., 2009), a representative sample of nighttime drivers of noncommercial motor vehicles on Fridays and weekend nights in the 48 contiguous states, following procedures similar to the three prior NRS studies in 1973, 1986, and 1996 (Lacey et al., 2009). The survey sites were selected from 60 primary sampling units of the National Analysis Sampling System/General Estimates System (NASS/GES) of NHTSA. The NASS/GES primary sampling units are cities, large counties, or groups of counties from within four regions of the country and three levels of population density. We selected the survey locations by placing a 1-mile grid over the area patrolled by the police department and then randomly selected square-mile areas that contained safe off-road locations in which the survey could be conducted. Drivers were randomly selected from the traffic flow at those sites and recruited for participation in the survey (Lacey et al., 2011). We conducted the surveys during 2-hour periods from 9:30 to 11:30 a.m. and 1:30 to 3:30 p.m. on Fridays and from 10 p.m. to midnight (referred to as the “evening period”) and 1 to 3 a.m. (referred to as the “nighttime period”) on Fridays and Saturdays. Data from the daytime collection periods on Fridays were not included in the previous NRS and therefore are excluded from this comparative study. A total of 6,823 drivers from the 2007 NRS evening and nighttime periods served as comparisons in this pseudo case-control study. For the 2007 NRS, we collected information on the age, gender, and BAC (among other characteristics) of drivers, using a preliminary breath-test device to measure BACs.

Approximately 5% of the BAC information in the target population of the 2007 NRS is missing because of refusals to participate or logistical problems. The missing BACs were imputed using a single imputation technique based on a two-stage procedure, as described in Lacey et al. (2009). Specifically, in the first stage, we classified the drivers with missing BACs into two categories—zero or positive BAC—and then, using a logistic model, we included as covariates the preliminary breath-test information and other driver characteristics. For those drivers for whom BAC was predicted as positive in the first stage, we imputed the BAC using linear regression. This process gave us a single imputation of the missing BACs. In general, a single imputation can lead to underestimation of the true variability because the uncertainty resulting from the imputation process is ignored. However, given the quite small proportion of missing BAC data in the 2007 NRS, the estimates of the standard errors of the coefficients in this particular case were not expected to be greatly affected by adopting this single-imputation approach. Thus, we assumed that the BAC information in the 2007 NRS was complete and that the imputation step had no influence in the variance estimation.

Crash data.

The 2006 and 2007 FARS, a census of motor-vehicle traffic crashes that resulted in a fatality within 30 days of the crash, served as the source of cases for this pseudo case-control study. The descriptions of each fatal crash reported in the FARS characterize the crash, the vehicles, and the people involved. In addition to the drivers’ characteristics collected in the FARS (e.g., age, gender, and race), the BACs of drivers and nonoccupants (pedestrians and bicyclists) are also recorded. However, in some cases the BACs are missing, mainly because drivers are not tested unless they are suspected of alcohol involvement or because of procedural limitations (e.g., medical examiners in rural areas not reaching a fatally injured driver on time for collecting a blood sample) (Hedlund et al., 2004). In the 2006 and 2007 FARS, about 40% of the BACs in the target population (drivers involved in fatal crashes) are missing. Rubin et al. (1998) suggested multiple imputation as a technique to handle missing BACs. In the method of multiple imputation, a missing BAC is replaced by a determined number of plausible values (e.g., 10), and appropriate analyses with complete data are performed to include the different sources of variability inherent to this procedure (Rubin, 1987; Subramanian, 2002). The 2006 and 2007 FARS databases include separate files with the 10 imputed BAC values for each year. To mimic the conditions of the 2007 NRS study, which serves as a comparison, we considered the FARS records of drivers of four-wheeled passenger vehicles who were between 16 and 97 years old and were involved in crashes that occurred during Friday and Saturday between 10 p.m. and 3 a.m. So that our crash inclusion criteria would match those of the 2007 NRS, we included only crashes outside of Indian country (i.e., areas either within a reservation, or land owned by the federal government held in trust for a tribe or tribal member; United States Code, Title 18, Part 1151) that occurred on paved roads not classified as an interstate, other urban freeway, or expressway, in counties with a population of at least 20,000 in 2006 and 2007, according to the U.S. Census. Following Zador et al. (2000), each crash-involved driver meeting the inclusion criteria was classified into one of six groups based on the number of vehicles involved in the crash and the driver’s involvement in a crash or fatal injury in a crash. The six categories are (a) fatally injured in a single-vehicle crash, (b) involved in a fatal single-vehicle crash, (c) fatally injured in a two-vehicle crash, (d) involved in a fatal two-vehicle crash, (e) all drivers killed in a fatal crash, and (f) all drivers involved in a fatal crash. The number of records in the 2006 and 2007 FARS by driver group is given in Table 1.

Table 1.

Number of drivers meeting the inclusion criteria in 2006 and 2007 FARS by group

Group No. of drivers
1. Fatally injured in a single-vehicle crash 2,501
2. Involved in a fatal single-vehicle crash 1,406
3. Fatally injured in a two-vehicle crash 842
4. Involved in a fatal two-vehicle crash 1,476
5. Fatally injured in a vehicle crash 3,495
6. Involved in a fatal vehicle crash 3,368
Open in a new tab

Notes: FARS = U.S. Fatality Analysis Reporting System. The “involvement” categories include drivers who were involved in a fatal vehicle crash but were not fatally injured.

Analyses

Estimating the relative risk of a fatal crash.

Our analytical strategy closely follows that of Zador et al. (2000). In that study, the authors provided a detailed justification for the use of the fatality (FARS) and exposure (NRS) data to estimate the RR. Briefly, the RR of a fatal crash between two groups (e.g., drivers with positive BACs and sober drivers) is estimated comparing the fatality/exposure ratio between the two groups, which is calculated using the FARS and NRS information, respectively. As in Zador et al. (2000), we approximated the RR of a fatal crash by computing its odds ratio. An odds ratio provides very accurate estimates of RR when the frequency of the targeted disease (e.g., crashes) is small relative to the exposed population (e.g., drivers) (Agresti, 2002).

As is standard practice in epidemiology, we applied logistic regression to estimate the RR. We modeled the probability of a fatal crash as a function of the driver’s BAC, controlling for possible confounders, such as gender and age. The logistic regression involved a binary response that takes 0/1 values, depending on whether the driver belongs to the “case” population (NHTSA, 2011) or the comparison population (2007 NRS). Thus, we only considered three possible predictors for the RR of a fatal crash—gender, age, and BAC—and all the possible interactions among them. Drivers were classified into three age groups: 16–20 years, 21–34 years, and 35 years and older. We also considered models that included either categorical or continuous BACs. In models with categorical BACs, they were redefined into seven categories (Zador et al., 2000): .00%, .001%–.019%, .020%–.049%, .050%–.079%, .080%–.099%, .100%–. 149%, and .150% and higher.

Model 1 illustrates the logistic model to estimate the RR, main effects only, and continuous BAC. Let pij(i = 1, 2; j = 1, 2, 3) be the probability of a fatal crash given the gender i, age group j, and BAC of a driver. The logistic model for pij is given by:

graphic file with name jsad341equ1.jpg

where the logit transformation is defined by logit(pij) =log [Pij / (1 − pij)]. Some coefficients in Model 1 are set to 0 because of the presence of redundant information in the design matrix of the model. For instance, gender is represented only by one variable that takes 0/1 values depending on the reference category (e.g., females). Under Model 1, the approximate RR between drivers who have a positive BAC and drivers who are sober of the same gender and age group is given by exp (â3BAC); here “exp” stands for exponentiation, and â3 represents the expected change of the RR in the logarithmic scale for the presence of one additional BAC unit. To avoid extremely small coefficient estimates, the actual and imputed BAC values were rescaled by a factor of 1,000 (Zador et al., 2000). Although not shown in (1), interactions between BAC, age group, and gender were also tested in our model.

Variance estimation.

Variance estimation of survey-based estimators with missing data should take both the sampling design and imputation process into account. Exposure data (e.g., from the 2007 NRS) were collected following a sampling design described in Lacey et al. (2009). Fatality data were obtained from a census of fatal crashes (FARS). Missing BACs in FARS have been imputed using a multiple imputation approach adopted by NHTSA (Subramanian, 2002). To address these complexities, we applied a replication method to account for the variability attributable to the sample design (Brick et al., 2000). We applied the delete-one jackknife method that has been suggested as appropriate for multistage designs with a small sampling fraction of units selected in the first stage (Levy and Lemeshow, 2008). This is the case for the 2007 NRS for which the sampling fraction in the first sampling stage is about 6% of all primary sampling units. The delete-one jackknife method deletes one primary sampling unit at a time from the full sample to create replicate weights, with the number of replicates being equal to the number of primary sampling units. The replicate weights are then modified by a factor called the “jackknife factor,” which is equal to ár = (R − 1) / R, where R is the number of primary sampling units. For our analyses, we created 60 replicate weights to estimate standard errors corresponding to the 60 primary sampling units included in the first stage of the sampling design (Lacey et al., 2009). The replicate weights leaving the rth primary sampling unit out are equal to 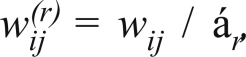Inline graphic where wij is the sampling weight for the ith driver in the jth primary sampling unit, j = 1, . . ., 60. These sampling weights were calculated with the information of the different stages involved in the sampling design (Lacey et al., 2010). We applied the PROC SURVEY-LOGISTIC procedure of the SAS software, Version 9.2, of the SAS System for Windows (SAS Institute Inc., Cary, NC).

According to Subramanian (2002), the missing BACs from the 2006 and 2007 FARS have already been imputed 10 times, and the variability inherent to the imputation process was properly incorporated into the estimates of the standard errors of the coefficients in the logistic model. Details of how to combine the estimates resulting from the 10 imputed BAC data sets can be found in Rubin et al. (1998). Inference for parameters in the logistic models based on multiple imputations was performed using SAS PROC MIANALYZE (Berglund, 2010).

Estimates were thus obtained by using each imputed data set and the 60 replicate weights based on the delete-one jackknife method, and this procedure was repeated for each of the 10 imputed FARS data sets. The resulting partial estimates were subsequently combined to obtain the final estimates of interest with their respective standard errors. These estimates take both the first-stage of the NRS 2007 sampling design and the FARS BAC imputation process into account. Wald confidence intervals (CIs) of coefficients for RRs were subsequently estimated.

For each model, we also computed the maximum of res-caled R2, a modified version of the generalized coefficient of determination that is used to measure the goodness-of-fit in logistic models (Menard, 2000). This statistic resembles the coefficient of determination in linear regression. Values of maximum of rescaled R2 near 1 indicate a good performance of the model. For logistic regression, however, values about .50 are still reasonable.

Results

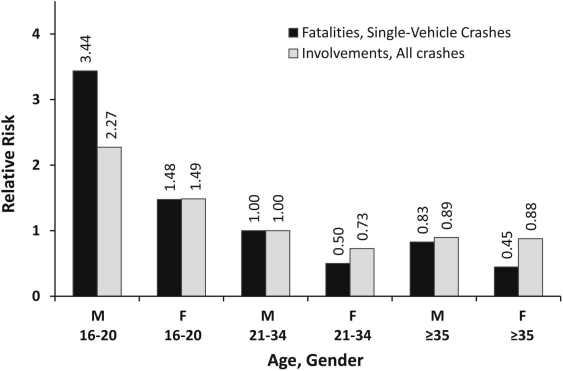
The RR of fatalities for sober drivers (BAC = .00%) involved in single-vehicle and all crashes separately by age group and gender, relative to sober male drivers ages 21–34, is shown in Figure 1. The RR for sober drivers decreases with age, although (a) this trend is more pronounced for drivers fatally injured in single-vehicle crashes and (b) the RR for female drivers involved in fatal crashes levels off after age 21 (i.e., the RR difference between female driver groups ages 21–34 and 35 and older was statistically nonsignificant). Within the same age group, the RR for fatally injured sober drivers varies with gender. This difference by gender is particularly noticeable for underage drivers (<21 years) involved in single-vehicle crashes. The risk of underage sober drivers involved in single-vehicle crashes is about 3.4 for males and 1.5 for females relative to sober male drivers ages 21–34. These values are significantly larger than their corresponding values in 1996 (about 1.7 and 1.2; see Zador et al., 2000, Figure 1). Compared with multiple-vehicle crashes, the relatively high RR of involvement in a single-vehicle crash for sober underage male drivers seems to decline with age (e.g., older drivers are relatively more involved in all crashes than they are in single-vehicle crashes). This finding may reflect the relative inexperience of young, sober, male drivers. Interestingly, sober female drivers were less likely to be fatally injured in a single-vehicle crash than to be involved in any fatal crash. This was true for every age group, but the size of the difference increased with age. This suggests that, relative to male drivers, all female drivers were less likely to be solely responsible for any crash in which they were involved. Further, the female drivers’ share of responsibility for crashes decreased with age. Similar results in RR comparisons for 1996 between fatally injured sober drivers were reported by Zador et al. (2000).

Figure 1.

Figure 1

Open in a new tab

Risk of driver fatalities in single-vehicle crashes and drivers’ involvement in fatal crashes at a blood alcohol concentration of .00%, by age and gender, relative to men ages 21–34 years. The “Involvement” category includes drivers who were involved in a fatal vehicle crash but were not fatally injured. M = male; F = female.

Table 2 displays the point estimates and standard errors of the coefficients in the logistic models fitted for fatalities and involvements of single, two-vehicle, and all crashes. These models include eight coefficients corresponding to main effects of gender, age group, continuous BAC, two-way interactions terms between BAC and age group, and a term representing the effect of low BAC (<.019%) and underage drivers. The last term is called the “dip effect” in the Grand Rapids study (Carr et al., 1974), and it serves to adjust the RR between drivers who have low BACs (<.019%) and drivers who are sober belonging to the underage group (Hurst et al., 1994; Zador et al., 2000). We fitted different models, including those with two-way and three-way interactions as well as categorical BACs. However, the models including more terms did not show better performance compared with those shown in Table 2, which reasonably describe the association between RR and BAC, and gender and age groups. The nonsignificance of the three-way interaction between BAC, gender, and age group, for example, may be because of the lack of power to detect these effects given the data sources available. More-over, the different sources of variability incorporated into the inference process may considerably increase the standard errors of the coefficients, making the detection of any significant effect more difficult, if it exists. Fatally injured drivers involved in single-vehicle and all-vehicle crashes have the largest max-rescaled coefficients of determination (72% and 64%, respectively), which means the goodness, of fit of the logistic models for these two groups is better compared with the other driver groups. Several alternative models were fitted for the driver groups with small coefficients of determination (about 30%), but no superior performance of these models was observed.

Table 2.

Logistic regression coefficients (standard errors) in models for risk of driver fatalities and driver involvement in single-vehicle crashes, in two-vehicle crashes, and in all crashes as a function of variables for age, gender, and BAC. Data are from the 2006–2007 FARS and 2007 National Roadside Survey.

Variable Single-vehicle crashes
 Two-vehicle crashes
 All crashes
Fatalities Involvements Fatalities Involvements Fatalities Involvements
Main effects
 Intercept −2.595 (0.205) −2.234 (0.202) −2.996 (0.207) −1.982 (0.208) −2.021 (0.210) −1.251 (0.209)
 Female −0.786 (0.078) −0.371 (0.066) −0.159 (0.070) −0.332 (0.064) −0.496 (0.068) −0.287 (0.065)
 Age (ref. = 21–34)
  Age 16−20 1.138 (0.084) 0.946 (0.089) 0.673 (0.085) 0.697 (0.084) 0.968 (0.083) 0.773 (0.084)
  Age ≥35 −0.231 (0.078) −0.119 (0.064) 0.289 (0.064) −0.050 (0.060) 0.079 (0.062) −0.040 (0.059)
 BrAC 0.035 (0.003) 0.028 (0.003) 0.025 (0.002) 0.022 (0.003) 0.031 (0.002) 0.024 (0.003)
Interactions
 0< BrAC <.019, age ≥ 21 −0.538 (0.166) −1.570 (0.197) −1.597 (0.161) −1.254 (0.168) −0.911 (0.165) −1.481 (0.174)
 Age 16−20, BrAC 0.004 (0.005) 0.005 (0.005) 0.004 (0.005) 0.003 (0.005) 0.004 (0.005) 0.004 (0.005)
 Age 21−34, BrAC (ref.)
 Age ≥35, BrAC −0.001 (0.004) −0.004 (0.004) −0.001 (0.003) −0.001 (0.004) −0.003 (0.003) −0.003 (0.004)
Max-rescaled R2 .7192 .3734 .3756 .2645 .6355 .3215
Open in a new tab

Notes: Coefficients marked in bold are not significant (5%). The “Involvement” categories include drivers who were involved in a fatal vehicle crash but were not fatally injured. BAC = blood alcohol concentration; FARS = U.S. Fatality Analysis Reporting System; BrAC (breath alcohol concentration) is the rescaled BAC: BrAC = BAC × 1000. Ref. = reference group: Men ages 21–34 years. Age ≥ 21 refers to ages 21 and older.

The models suggest that the risk of being fatally injured or involved in fatal crashes in single, two, and more vehicles depends on the BAC and age group, with underage drivers having a greater risk compared with sober male drivers ages 21–34. Older drivers (≥35 years) have smaller risk compared with the same reference group. We found no significant differences between the RR of males and females in any driver group.

Based on the logistic models presented in Table 2, we estimated the proportionate increase of RR of driver fatalities and involvement associated with a .02% increase in BAC, as shown in Table 3. The respective 95% CIs are also given in that table. Those factors are larger for fatally injured drivers involved in single-vehicle crashes. The proportionate factor increase is also larger for fatalities in all the driver groups. Those proportionate factors also decrease with age, with underage drivers having larger proportionate factors. In general, the proportionate factors in this study do not show significant differences from the 1996 NRS/FARS results (Zador et al., 2000, Table 3) if the CIs are considered. If we merely compare the point estimates of the proportionate factors, however, the 2006–2007 proportionate factors for underage drivers are smaller compared with the same group in the 1996 NRS/FARS study, whereas the 2006–2007 proportionate factors are larger for older drivers compared with the 1996 NRS/FARS results.

Table 3.

Model-based estimates for factor of proportionate increase in the relative risk of driver fatalities and driver involvement associated with a .02% increase in BAC; 95% confidence intervals are in brackets

Age, in years Single-vehicle crashes
 Two-vehicle crashes
 All crashes
Fatalities Involvements Fatalities Involvements Fatalities Involvements
16–20 2.16 [1.59, 2.92] 1.91 [1.38, 2.63] 1.8 [1.38, 2.35] 1.66 [1.25, 2.2] 2.04 [1.55, 2.69] 1.76 [1.32, 2.33]
21–34 2.01 [1.81, 2.24] 1.74 [1.55, 1.94] 1.66 [1.52, 1.8] 1.56 [1.41, 1.72] 1.88 [1.71, 2.06] 1.62 [1.47, 1.79]
≥35 1.96 [1.52, 2.54] 1.61 [1.23, 2.12] 1.62 [1.31, 2] 1.54 [1.22, 1.48] 1.78 [1.42, 2.23] 1.54 [1.21, 1.95]
Open in a new tab

Notes: ≥35 denotes ages 35 years and older. The “Involvement” categories include drivers who were involved in a fatal vehicle crash but were not fatally injured. BAC = blood alcohol concentration.

In Table 4, we estimated the RR (relative to BAC = .00%) and their respective 95% CIs for fatalities in single-vehicle crashes and involvements in all crashes by age group and BAC class. The RR estimates in Table 4 are based on the results of the logistic models in Table 2. For each BAC class, the numbers correspond to the estimates of the RR for the midpoint of the BAC class and a given age group relative to sober drivers (BAC = .00%) in the same age group. For instance, the RR equal to 1.47 in the first row of Table 4 is the RR of fatally injured drivers ages 16–20 with BACs of .015% relative to fatally injured sober drivers ages 16–20. This RR estimate is a reasonable number to represent the RR of drivers with BACs between .001% and .019%. The RR of being fatally injured in a single-vehicle crash and involved in a fatal crash increases considerably as the BAC goes up. This pattern is more remarkable in fatalities in single-vehicle crashes. For instance, the risk of a driver ages 16–20 with a BAC between .020% and .049% being fatally injured in a single-vehicle crash could be around 3.8 (95% CI [2.9, 5.1]) times the risk of a sober driver in the same age group. The risk of being fatally injured and involved in a crash relative to sober drivers in the same age group decreases with age; thus, underage drivers are the group with the largest risk. The risk of being fatally injured in a single-vehicle crash is greater than for all crashes, regardless of age group.

Table 4.

Model-based relative risk of driver fatalities in single-vehicle crashes and driver involvement in all fatal crashes as a function of driver BAC by gender and age, relative to sober drivers of the same age and gender

Age, in years Crash type 0 BAC
.001%–.019% .020%–.049% .050%–.079% .080%–.099% .100%–. 149% ≥.150%
16–20 FSV 1 1.47 3.84 12.18 31.86 122.43 4,727.95
– [1.35, 1.6] [2.86, 5.16] [7.05, 21.04] [14.95, 67.92] [42.79, 350.27] [743.36, 30070.8]
IAll 1 1.33 2.68 6.24 12.61 33.79 490.41
– [1.23, 1.43] [2.06, 3.48] [3.84, 10.12] [6.45, 24.65] [13.31,85.73] [95.23, 2525.41]
21–34 FSV 1 0.83 3.40 9.68 23.18 78.68 2171.46
– [0.61, 1.12] [2.81, 4.1] [6.82, 13.74] [14.27, 37.65] [40.1, 154.37] [663.17, 7110.12]
IAll 1 0.29 2.32 4.78 8.74 20.30 200.03
– [0.21, 0.4] [1.95, 2.77] [3.46, 6.61] [5.58, 13.68] [10.89, 37.82] [66.91, 598.03]
≥35 FSV 1 0.82 3.26 8.98 20.89 68.12 1684.92
– [0.58, 1.16] [2.86, 3.71] [7.06, 11.43] [14.96, 29.17] [42.85, 108.3] [745.09, 3810.21]
IA11 1 0.28 2.12 4.03 6.89 14.59 111.94
– [0.2, 0.4] [1.9, 2.36] [3.3, 4.93] [5.21, 9.11] [9.91, 21.5] [56.61, 221.34]
Open in a new tab

Notes: Source of data: 2007 National Roadside Survey and the 2006–2007 U.S. Fatality Analysis Reporting System. 95% confidence intervals of relative risk are in brackets. Relative risk corresponds to the relative risk at the midpoint of the BAC interval (i.e., .015, .035, .065, .090, .125, and .220). BAC = blood alcohol concentration; FSV = fatalities in single-vehicle crashes; IAll = involvement in all fatal crashes (involvement denotes drivers who were involved in a fatal vehicle crash but were not fatally injured).

Considering the CI estimates in 1996 and those in 2006 and 2007, there are no overall significant differences between the two studies in the risk of a fatal crash in single-vehicle crashes and all crashes. The 2007 models showed no differences between males and females in any age group; therefore, we presented only one estimate for each age group in Table 4. The corresponding Table 4 (Zador et al., 2000) from the 1996 study lists risk estimates separately for males and females because, although there were no differences between adult men and women (as shown by the identical risk estimate values found in the table for adult men and women), the 1996 study did find a significant difference between sexes in the underage group. In our models, the overall probability of a crash depends on gender, but when the risk of a crash is analyzed as a function of BAC relative to the same age group, we did not find a significant difference by gender (e.g., RR curves by gender do not show a different rate of change as a function of BAC).

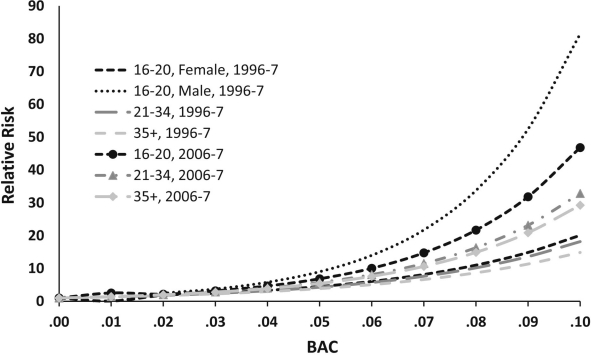
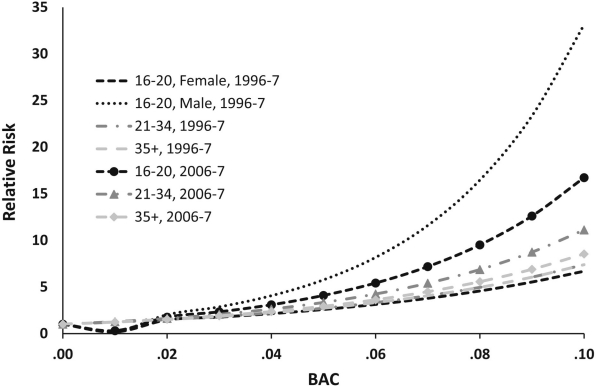
Figures 2 and 3 present the data from Table 4 in graphic form, contrasting the results from the Zador et al. analysis of the 1996 data with our 2007 analysis. The RR scale is substantially higher for single-vehicle crashes, in which only one driver is involved and typically viewed as responsible, compared with all crashes, where more than one driver may share responsibility. Thus, for a young male driver (ages 16–20) in 1996, the risk of being in a fatal single-vehicle crash with a BAC of .10% is 80 times that of a similar driver with a zero BAC, whereas the risk of being in any fatal crash is only 30 times that at a zero BAC. The most striking feature of the RR graphs is the difference between risk curves for underage male and female drivers. The 1996 study found a substantial difference in risk between underage males and females, with male drivers exhibiting about four times the RR of being in a fatal crash at a BAC of .10% as were females. However, in 2007, the RR for underage males and females did not differ significantly. Although there were no significant differences between the RR of adult men and women in either 1996 or 2007, there was a slight, nonsignificant trend for adult drivers to have higher RRs in 2007.

Figure 2.

Figure 2

Open in a new tab

Relative risk curve—single-vehicle crash fatalities. BAC = blood alcohol concentration.

Figure 3.

Figure 3

Open in a new tab

Relative risk—involvement in all crashes. Involvement denotes drivers who were involved in a fatal vehicle crash but were not fatally injured.

Discussion

Eleven years separate the RR study reported here from that conducted by Zador et al. During that interval of 1996 to 2007, the percentage of all fatal crashes involving alcohol-impaired (BAC ≥ .08%) drivers has remained unchanged, at approximately 22%. This suggests that the driving environment, vehicles, and driver behavior has changed little over that period and leads to the expectation that the RR of crash involvement as a function of BAC has not changed. This study repeated as closely as possible the analytic procedures of the original analysis, substituting comparison data from the 2007 NRS for the 1996 roadside survey data. The overall RR level for adults in 2007 was slightly elevated over that of 1996, but the difference was not statistically significant (Figures 2 and 3). Both studies found that the expected reduction in RR was associated with increased age (Figure 1), and both found that the RR curve for adult men and women did not differ significantly (Figures 2 and 3). Although the higher risk of crash involvement for underage drinking drivers has been widely recognized, the fact that, given equal BACs, males and females have the same RR of crash involvement has been less well understood. Because women typically consume less alcohol than men do, they are less frequently arrested for impaired driving and are less frequently involved in alcohol-related crashes. Nevertheless, at a given BAC level, their risk is the same as for men: an important consideration for both prevention and law enforcement.

The primary differences between the 1996 and 2007 analyses involved underage drivers. The 2007 analysis found that, compared with drivers ages 21–34, sober underage drivers were at higher risk than estimated in the 1996 study. This finding seems somewhat surprising because the 1996–2007 period was marked by the trend for states to enact graduated driver licensing (GDL) laws, which increase the age at licensing and extend the period of adult supervision of the novice driver. There is extensive evidence that GDL laws reduce 16- and 17-year-old fatalities (Hedlund et al., 2006; Ulmer et al., 2000). We provide two speculative arguments to explain our finding that sober underage drivers are at a higher risk than in the previous decade. First, we speculate that the passing of GDL laws not only reduced the number of fatalities among drivers ages 16–20, but it also reduced the number of drivers at these ages who drive at night, mainly because of GDL nighttime driving restrictions (the proportion of drivers ages 16–20 in the 1996 NRS and the 2007 NRS decreased from 18% in 1996 to 15% in 2007). Nevertheless, those who drive at those hours are more likely to be risk takers than are the average underage drivers. Second, we speculate that the observed increase in crash risk for sober drivers may also be attributed to an increase over the last decade in risk-driving behaviors and activities unrelated to alcohol, such as texting or cell phone use. Whatever the cause of the observed doubling of the RR (3.4 in 2007 compared with 1.7 in 1996) for underage sober male drivers, further research is needed to explain this finding.

Historically, RR studies have found a substantial difference in the alcohol-related risk of underage males and females. This is shown in Figures 2 and 3 for the 1996 survey where males younger than 21 have a seven times higher RR at a BAC of .10%. It is striking that, in the 2007 analysis, the RR for underage men is not significantly different from that for underage women. This is consistent with the growing literature on the change in the driving status of women. Further, some evidence suggests that female drivers are increasingly vulnerable to crashes, although it is not clear if such change is caused by female drivers becoming greater risk takers or having more exposure to crashes (Laapotti et al., 2001; Mayhew et al., 2003; Romano et al., 2008). This leads to the question of whether some age/gender groups (young females in this study) are at a higher risk of alcohol-related crashes than previously measured. Because female drivers are viewed to be at a much smaller crash risk than male drivers, current prevention efforts focus largely on men, particularly young men. If women are increasingly taking more driving risks compared with young male drivers, policymakers should evaluate the benefits of devoting more resources to address this relatively neglected group’s risky behavior. Although this study does not reveal gender-based differences for adult drivers, this increased RR for underage females may be a cohort effect that will manifest more in older drivers over time.

This study has a number of limitations: The sampling and record-keeping procedures for the FARS are standardized; thus, the only source of significant errors in the risk calculations for 1996 or 2007 is the presence of missing BAC data. However, although the sampling procedures of the two NRS studies (1996 and 2007) were standardized insofar as possible to maintain continuity with previous national roadside surveys (Lacey et al., 2009), it is probable that some inevitable variations in collection procedures contribute to the error in the comparison of the RR levels in 1996 and 2007. Because we relied on different data sources, standard errors of the estimated parameters were larger than they otherwise would have been, causing a reduction in the statistical power associated with the contrasts we made. It is also important to keep in mind that the FARS data are based on blood tests collected at varying periods following the crash and transported for some distance in the 50 states to laboratories in which the equipment and capabilities vary significantly. Although roadside BAC data are based on breath tests measured immediately, some errors are to be expected from collecting samples under roadside conditions.

Even with limitations, the NRS data are valuable for determining and tracking RR data for driver groups of interest. Classical, full case-control studies, such as that of Blomberg et al. (2005), have made an important contribution to science, but they are expensive. The NRS studies are being conducted every decade and may be mounted more frequently in the future (the next one is scheduled for 2013) to track changes in alcohol prevalence among drivers. Combining the NRS data with the FARS data provides researchers with a relatively inexpensive way to track RR data over time.

Acknowledgments

The authors thank an anonymous reviewer for his or her detailed and very helpful comments.

Footnotes

Data collection was supported by National Highway Traffic Safety Administration Contract No. DTNH 22-06-C-00040 and National Institute on Alcohol Abuse and Alcoholism (NIAAA) Grant R01 AA016407. Data analyses were supported by NIAAA Grants R21 AA018158-01A2 andP20 AA017831.

References

  1. Agresti A. Categorical data analysis. 2nd ed. Hoboken, NJ: John Wiley & Sons; 2002. [Google Scholar]
  2. Berglund PA. An introduction to multiple imputation of complex sample data using SAS v9.2 (Paper 265-2010) SAS Global Forum 2010: Statistics and Data Analysis. 2010 Retrieved from http://support.sas.com/resources/papers/proceedings10/265-2010.pdf. [Google Scholar]
  3. Blomberg RD, Peck RC, Moskowitz H, Burns M, Fiorentino D. Crash risk of alcohol involved driving: A case-control study. Stamford, CT: Dunlap & Associates; 2005. Retrieved from http://www.dunla-pandassociatesinc.com/crashriskofalcoholinvolveddriving.pdf. [Google Scholar]
  4. Borkenstein RF, Crowther RF, Shumante RP, Ziel WB, Zylman R. The role of the drinking driver in traffic accidents. Bloom-ington, IN: Department of Police Administration, Indiana University; 1964. [Google Scholar]
  5. Brick JM, Morganstein D, Valliant R. Analysis of complex sample data using replication (technical report) Rockville, MD: Westat; 2000. Retrieved from http://westat.nl/Westat/pdf/wesvar/ACS-Replication.pdf. [Google Scholar]
  6. Carr B, Borkenstein RF, Perrine MW, Van Berkom LC, Voas RB. International conference on research methodology for roadside surveys of drinking-driving — alcohol countermeasures workshop. (Final Report No. DOT HS 801 220) Washington, DC: National Highway Traffic Safety Administration; 1974. Retrieved from http://ntl.bts.gov/lib/25000/25300/25376/DOT-HS-801-220_002.pdf. [Google Scholar]
  7. Chen LH, Baker SP, Li G. Graduated driver licensing programs and fatal crashes of 16-year-old drivers: A national evaluation. Pediatrics. 2006;118:56–62. doi: 10.1542/peds.2005-2281. [DOI] [PubMed] [Google Scholar]
  8. Fell JC, Voas RB. The effectiveness of reducing illegal blood alcohol concentration (BAC) limits for driving: Evidence for lowering the limit to .05 BAC. Journal of Safety Research. 2006;37:233–243. doi: 10.1016/j.jsr.2005.07.006. [DOI] [PubMed] [Google Scholar]
  9. Hedlund JH, Shults RA, Compton R. Graduated driver licensing and teenage driver research in 2006. Journal of Safety Research. 2006;37:107–121. doi: 10.1016/j.jsr.2006.02.001. [DOI] [PubMed] [Google Scholar]
  10. Hedlund JH, Ulmer RG, Northrup VS. State laws and practices for BAC testing and reporting drivers involved in fatal crashes. (DOT HS 809 756) Washington, DC: National Highway Traffic Safety Administration; 2004. Retrieved from http://www.nhtsa.gov/people/injury/alcohol/bac-testing/images/State%20Laws_low.pdf. [Google Scholar]
  11. Hurst PM, Harte D, Frith WJ. The Grand Rapids dip revisited. Accident Analysis & Prevention. 1994;26:647–654. doi: 10.1016/0001-4575(94)90026-4. [DOI] [PubMed] [Google Scholar]
  12. Laapotti S, Keskinen E, Hatakka M, Katila A. Novice drivers’ accidents and violations—A failure on higher or lower hierarchical levels of driving behaviour. Accident Analysis & Prevention. 2001;33:759–769. doi: 10.1016/s0001-4575(00)00090-7. [DOI] [PubMed] [Google Scholar]
  13. Lacey J, Brainard K, Snitow S. Drug per se laws: A review of their use in states. (Report No. DOT HS 811 317) Washington, DC: National Highway Traffic Safety Administration; 2010. Retrieved from http://www.nhtsa.gov/staticfiles/nti/impaired_driving/pdf/811317.pdf. [Google Scholar]
  14. Lacey JH, Kelley-Baker T, Voas RB, Romano E, Furr-Holden CD, Torres P, Berning A. Alcohol- and drug-involved driving in the United States: Methodology for the 2007 National Roadside Survey. Evaluation Review. 2011;35:319–353. doi: 10.1177/0193841X11422446. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Lacey JH, Kelley-Baker T, Furr-Holden D, Voas R, Moore C, Brainard K, Berning A. 2007 National Roadside Survey of Alcohol and Drug Use by Drivers: Methodology (Report No. DOT HS 811 237) Washington, DC: National Highway Traffic Safety Administration; 2009. Retrieved from http://www.nhtsa.gov/staticfiles/nti/pdf/811237.pdf. [Google Scholar]
  16. Levy PS, Lemeshow S. Sampling of populations: Methods and applications. 4th ed. Hoboken, NJ: Wiley; 2008. [Google Scholar]
  17. Mayhew DR, Simpson HM, Pak A. Changes in collision rates among novice drivers during the first months of driving. Accident Analysis & Prevention. 2003;35:683–691. doi: 10.1016/s0001-4575(02)00047-7. [DOI] [PubMed] [Google Scholar]
  18. Menard S. Coefficients of determination for multiple logistic regression analysis. American Statistician. 2000;54:17–24. [Google Scholar]
  19. Moskowitz DB, Robinson CD. Driving-related skills impairment at low blood alcohol levels. In: Noordzij PC, Roszback R, editors. Alcohol drugs and traffic safety, T86: Proceedings of the 10th international conference on alcohol, drugs, and traffic safety Amsterdam, 9–12 September 1986 (International Congress Series) Amsterdam, The Netherlands: Elsevier; 1987. pp. 79–86. [Google Scholar]
  20. National Highway Traffic Safety Administration. Fatality Analysis Reporting System (FARS): Detailing the Factors Behind Traffic Fatalities on our Roads. Washington, DC: National Highway Traffic Safety Administration; 2011. Retrieved from http://www.nhtsa.gov/FARS. [Google Scholar]
  21. National Institute on Alcohol Abuse and Alcoholism. Ninth special report to the U.S. Congress on alcohol and health from the Secretary of Health and Human Services (NIH Publication No. 97-4017, Ch. 7, pp. 247–274) Rockville, MD: National Institutes of Health; 1997. Effects of alcohol on behavior and safety. Retrieved from http://www.eric.ed.gov/PDFS/ED418362.pdf. [Google Scholar]
  22. Romano E, Kelley-Baker T, Voas R. Young impaired drivers: The nature of the problem and possible solutions (Transportation Research Circular No. E-C132, pp. 18–23) Washington, DC: Transportation Research Board of the National Academies; 2009. Females and alcohol-related fatal crashes: Exposure-adjusted trends. Retrieved from http://onlinepubs.trb.org/onlinepubs/circulars/ec132.pdf. [Google Scholar]
  23. Romano E, Kelley-Baker T, Voas RB. Female involvement in fatal crashes: Increasingly riskier or increasingly exposed? Accident Analysis & Prevention. 2008;40:1781–1788. doi: 10.1016/j.aap.2008.06.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Rubin DB. Multiple imputation for nonresponse in surveys. New York, NY: Wiley; 1987. [Google Scholar]
  25. Rubin DB, Schafer JL, Subramanian R. Multiple imputation of missing blood alcohol concentration (BAC) values in FARS. Washington, DC: National Highway Traffic Safety Administration; 1998. [Google Scholar]
  26. Shults RA, Elder RW, Sleet DA, Nichols JL, Alao MO, Carande-Kulis VG, Thompson RS the Task Force on Community Preventive Services. Reviews of evidence regarding interventions to reduce alcohol-impaired driving. American Journal of Preventive Medicine, 21. 2001;Supplement 1:66–88. doi: 10.1016/s0749-3797(01)00381-6. [DOI] [PubMed] [Google Scholar]
  27. Subramanian R. Transitioning to multiple imputation— A new method to impute missing blood alcohol concentration (BAC) values in FARS (Report No. DOT HS 809 403) Washington, DC: National Center for Statistics and Analysis; 2002. Retrieved from http://www-nrd.nhtsa.dot.gov/Pubs/809-403.PDF. [Google Scholar]
  28. Ulmer RG, Preusser DF, Williams AF, Ferguson SA, Farmer CM. Effect of Florida’s graduated licensing program on the crash rate of teenage drivers. Accident Analysis & Prevention. 2000;32:527–532. doi: 10.1016/s0001-4575(99)00074-3. [DOI] [PubMed] [Google Scholar]
  29. Voas RB, Tippetts AS, Fell JC. Assessing the effectiveness of minimum legal drinking age and zero tolerance laws in the United States. Accident Analysis & Prevention. 2003;35:579–587. doi: 10.1016/s0001-4575(02)00038-6. [DOI] [PubMed] [Google Scholar]
  30. Zador PL. Alcohol-related relative risk of fatal driver injuries in relation to driver age and sex. Journal of Studies on Alcohol. 1991;52:302–310. doi: 10.15288/jsa.1991.52.302. [DOI] [PubMed] [Google Scholar]
  31. Zador PL, Krawchuk SA, Voas RB. Alcohol-related relative risk of driver fatalities and driver involvement in fatal crashes in relation to driver age and gender: An update using 1996 data. Journal of Studies on Alcohol. 2000;61:387–395. doi: 10.15288/jsa.2000.61.387. [DOI] [PubMed] [Google Scholar]

Articles from Journal of Studies on Alcohol and Drugs are provided here courtesy of Rutgers University. Center of Alcohol Studies

RESOURCES