Direct Upstream Motility in Escherichia coli

Abstract

We provide an experimental demonstration of positive rheotaxis (rapid and continuous upstream motility) in wild-type Escherichia coli freely swimming over a surface. This hydrodynamic phenomenon is dominant below a critical shear rate and robust against Brownian motion and cell tumbling. We deduce that individual bacteria entering a flow system can rapidly migrate upstream (>20 μm/s) much faster than a gradually advancing biofilm. Given a bacterial population with a distribution of sizes and swim speeds, local shear rate near the surface determines the dominant hydrodynamic mode for motility, i.e., circular or random trajectories for low shear rates, positive rheotaxis for moderate flow, and sideways swimming at higher shear rates. Faster swimmers can move upstream more rapidly and at higher shear rates, as expected. Interestingly, we also find on average that both swim speed and upstream motility are independent of cell aspect ratio.

Introduction

Bacterial motility is a crucial component of the pathogenesis of bacteria and has been extensively studied (1,2). An interesting feature of bacterial motility is how it interacts with or responds to various environmental factors so as to increase local colonization and survival (3). For example, certain motile microorganisms, such as the photosynthetic purple bacterium Rhodospirillum centenum, can sense and swim toward light conditions (i.e., phototaxis) that are optimal for growth in complex environments (4). Magnetospirillum magnetotacticum synthesizes linear chains of magnetic nanoparticles (5) that align the bacterium's motion with geomagnetic field lines (i.e., magnetotaxis), allowing it to seek optimal oxygen concentrations at sediment-water interfaces (6). Most motile bacteria, such as Escherichia coli, can chemotax to migrate toward nutrient-rich locations (7,8). E. coli also benefit from hydrodynamic interactions with their environments. They find surfaces (9,10), swim in circles over them for extended periods despite Brownian motion disturbances (11,12), and eventually attach (13), forming biofilms to evade host defenses (14). In the presence of flow, these hydrodynamic effects are more prominent, directing motile E. coli away from strong shear regions and toward quiescent routes along sidewalls or crevices for upstream migration (15). Simulation studies have also revealed a rich set of hydrodynamic interactions between neighboring swimmers within a dense group of motile bacteria (16,17).

Here, we provide an experimental demonstration of direct and continuous upstream motility (i.e., positive rheotaxis) in a freely swimming microorganism (wild-type (WT) E. coli). Upstream migration of E. coli is mediated by hydrodynamic forces and is quite robust against the disorienting effects of both Brownian motion and cell tumbling. We characterize the entire spectrum of cellular trajectories under different shear rates and demonstrate that the main behavior of flow-assisted orientation described by Hill et al. (15) is a special case that corresponds to high shear flows. Specifically, we find that there exists a critical shear rate below which direct, prolonged positive rheotaxis is dominant over completely flat, open surfaces away from sidewalls or crevices. This mode of direct upstream motility is distinct from yet complementary to the mechanism outlined by Hill et al. (15), which involves E. coli migrating orthogonal to the flow field before they can swim upstream near a sidewall. In this work, we present a complete characterization of E. coli motility under all hydrodynamic conditions near a flat, open surface.

Materials and Methods

Bacteria preparation

A WT E. coli strain (K12) was used in all experiments. Each week, cells from a frozen stock were streaked on 1.5% w/v Bacto agar plates containing Luria-Bertani (LB) broth (1% Bacto tryptone, 0.5% Bacto yeast extract, 0.5% NaCl at neutral pH, 0.2 μm filtered and autoclaved before use) and incubated for 16 h overnight at 30°C, followed by refrigeration at 4°C. Before an experiment run, a single colony from the plate was grown to saturation in LB broth for 16 h at 30°C with shaking, followed by preparation of a dilution sample (50 μl saturation culture in 5 ml LB broth) under the same conditions for 3 h. A motility plate (1% Bacto tryptone, 0.7% NaCl, and 0.25% Bacto agar) was then inoculated with <2 μl dilution culture and incubated at 30°C for 8 h. A saturation culture was started from the fastest swimmers in the motility plate, and the motility selection process was repeated 3–5 times until the radius of the migration ring in the motility plate exceeded 2 cm. A final dilution sample (5 ml saturation culture in 500 ml of LB broth) was prepared and incubated for 3 h at 30°C just before the experiment was conducted.

Microfluidic device construction

Two long rectangular strips were cut out of a polished silicon wafer and stacked at the center of an intact 3-inch diameter wafer to create a mold structure 590 μm high, 5.75 mm wide, and 4 cm long. The surface was passivated with tetra-methylchlorosilane (TMCS, Sigma Aldrich, St. Louis, MO), covered with a freshly prepared mixture of poly dimethylsiloxane (PDMS, Dow Corning, Midland, MI) base and curing agent (10:1 ratio), and baked at 80°C for 2 h to achieve a fully cured stamp over the mold (18). The patterned PDMS stamp was then cut out, inlet and outlet holes of the microfluidic channel were punched, and the stamp was attached to a clean 2 inch × 3 inch microscope glass slide after a brief treatment in a plasma oven (PDC-32G; Harrick Scientific, Ithaca, NY). The PDMS over the resulting microfluidic channel was thick enough to render pressure-related channel deformations negligible. Finally, teflon tubings (TFT20022; Alpha Wire, Elizabeth, NJ) were inserted to introduce the bacteria into the microchannel.

Experiment setup

Three plastic syringes (Becton Dickinson, Sparks, MD) of different sizes (1 ml, 10 ml, and 60 ml) were connected to the microfluidic device via Tygon (Saint Gobain, Garden Grove, CA) tubings (3/8 inch inner diameter) and manual fluid valves. Syringe pumps were used to generate flow at various shear rates in the vicinity of the microchannel ceiling, and rates of 0–1 s⁻¹, 1–10 s⁻¹, and 10–59 s⁻¹ were achieved with 1 ml, 10 ml, and 60 ml syringes, respectively. A custom fluidic filter was used to eliminate potential flow pulsations originating from the stepper motor driver of the syringe pumps.

We characterized bacterial trajectories by subjecting motile WT E. coli in LB broth to different shear flows within a microfluidic channel (Fig. 1 a). The wide microchannel provided an observation region in its center that offered constant shear rates near the top and bottom bounding walls (19). To eliminate excessively slow swimmers that would otherwise sediment, we focused on the top PDMS surface of the channel (Fig. 1 b). An automated computer imaging system recorded high-resolution images of bacteria swimming near the surface at 30–240 frames/s through a 40× objective (focal depth 2 μm) on an inverted microscope (Axiovert; Carl Zeiss, Jena, Germany). To obtain reliable statistics, we recorded and analyzed >300,000 near-surface swimming trajectories for flow rates up to 1000 μl/min (59 s⁻¹). The microfluidic device and the camera were oriented so as to result in bacteria drifting from the top to the bottom of the images, which were streamed and saved in real time to a high-speed hard disk system for later analysis.

Figure 1.

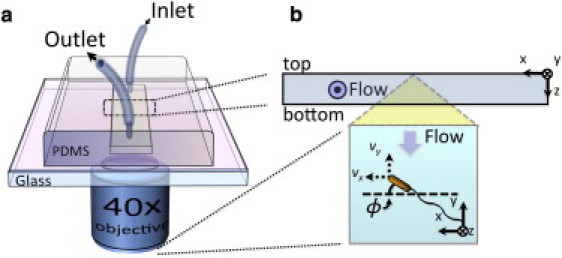
Experimental setup. (a) WT E. coli were subjected to various shear flows within a microfluidic channel and imaged from below in an inverted microscope setup. (b) Cells were observed at the center of the channel ceiling as they swam over its PDMS surface. In choosing a coordinate system for data analysis, we follow the convention of Kaya and Koser (19), where the +y axis points upstream and the z axis denotes the surface normal (for channel ceiling) pointing into the flow channel. In this convention, a positive y velocity component corresponds to upstream migration. The cell body orientation angle (ϕ) is measured relative to the +x axis. The microscope-camera system flips the images along the vertical image axis, such that the z axis points into the page in recorded pictures (see Fig. 3).

Image analysis

Image sequences were analyzed offline in MATLAB (The MathWorks, Natick, MA) using a modified optical-flow tracking algorithm (20). The script was customized to record not only the position but also the instantaneous orientation, width, and length of bacteria. The software joined E. coli positions obtained from separate sequential images into individual tracks and calculated the evolution of each bacterium's instantaneous swim speed via $v_n=\sqrt{{\left(x_{n+1}-x_n\right)}^2-{\left(y_{n+1}-y_n\right)}^2}$, where (x_n, y_n) denotes the bacterium's position in image n.

Background for analysis and interpretation

When a bacterium swims in circles over a surface, performs a random walk (including tumble-swim cycles), or is subject to the randomizing influence of rotational Brownian motion, it eventually samples all values of the cell body orientation angle (ϕ) within the plane of that surface with equal probability. Experimentally, this means that, when observed over a long enough time, the probability density function (PDF) of ϕ should be uniform (as simulated in Fig. 2 a). This is also true for the overall orientation angles of an entire population of bacteria, as long as the cell trajectories can be assumed to be independent and interactions between trajectories (such as collisions or hydrodynamic interactions) are random with no long-range correlations or event memory. When all bacteria swim at the same speed (v) under these conditions, the projection of that speed along a given primary axis of the surface (e.g., v_x = v cos(ϕ)) will have the simulated distribution depicted in Fig. 2 b. Note that the sinusoidal function acting on the uniform PDF of ϕ is responsible for the raised-U shape of the PDF for v_x and v_y. When v itself is a random variable with normal (Gaussian) distribution (as was the case for our E. coli population; Fig. 2 c), we can calculate the PDF of v_x and v_y using either analytical methods (21,22) or Monte Carlo simulations. For instance, we use the simulation approach shown in Fig. 2 d to obtain v_x when ϕ has a uniform PDF and v is a Gaussian random variable with 22.3 μm/s mean and 4.6 μm/s standard deviation, as measured in our experiments. This symmetric, zero-mean distribution for v_x indicates that the bacteria have no direction preference along the x axis. Any deviation from the double symmetric peaks in Fig. 2 d reflects a nonuniformity in the orientation angle ϕ and a corresponding preference to swim along the direction within the x axis indicated by the sign of the nonzero mean. If such a swimming direction preference exists, it would manifest as a clear asymmetry in the peak magnitudes of Fig. 2 d.

Figure 2.

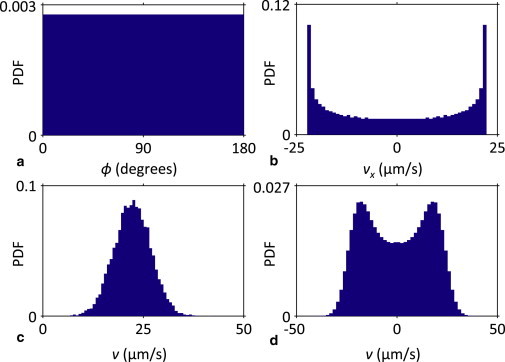
Bacteria orientation angles (ϕ) and swim speed components under no-flow conditions. (a) The simulated PDF of ϕ is uniform under circular or random swimming assumptions. (b) Assuming a constant swim speed (v = 22.3 μm/s), the corresponding velocity components along the x or y axes of the surface (v_x or v_y) have a characteristic U-shaped distribution, with their PDF peaking at ±v. (c) In reality, the measured swim speed of the bacteria is normally distributed (μ = 22.3 μm/s; σ = 4.6 μm/s at the beginning of the experiment). (d) The corresponding PDFs for v_x and v_y are M-shaped and symmetric about the origin.

Results

Overview

Under no-flow conditions, the bacteria exhibited circular swimming trajectories, as expected (mode I; Fig. 3 a). When flow was turned on, the bacteria quickly got aligned to face upstream (+y direction), with fast swimmers migrating directly and continuously upstream (mode II; Fig. 3 b). At faster shear rates, E. coli swam orthogonal to flow toward one side of the channel (+x direction) as they got dragged downstream (mode III; Fig. 3 c), replicating the hydrodynamic surface interaction that we described earlier (15). (In the work by Kaya and Koser (19), the surface coordinate axes labeling the images did not account for an image reflection in the microscope-camera system. In this work, we correct that issue and adopt a self-consistent surface coordinate system: the +y axis points into the flow and the +z axis is the surface normal pointing into the channel. Consequently, mode III sideways motion of E. coli is in the +x direction.)

Figure 3.

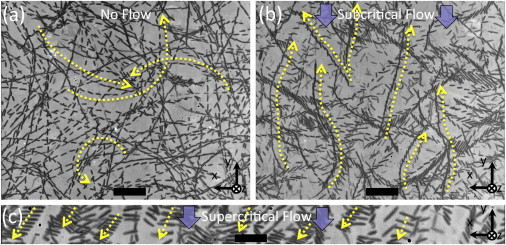
Sample bacterial trajectories. (a) Under quiescent conditions, bacteria swam in circular trajectories, occasionally tumbling or colliding, and randomly changing direction. (b) Once moderate laminar flow was introduced, most bacteria rapidly turned to face and swim upstream (i.e., positive rheotaxis; trajectories shown for 5.9 s⁻¹ shear). The overall population displayed positive rheotaxis until 6.4 s⁻¹. (c) At higher shear rates, an increasing percentage of bacteria succumbed to the drag from the flow and swam sideways to eventually get out of the fast shear (trajectories shown for 35 s⁻¹ shear). In a–c, images are contrast-enhanced composites comprising minimum pixels of every fifth sequential frame (20). Original frame rates: 30 frames/s for a and b, and 240 frames/s for c. See Movie S1, Movie S2, and Movie S3 for original image sequences.

Circular or random trajectories under no-flow conditions yielded an equal likelihood for all cell body orientations within the x-y plane, resulting in a uniform distribution of orientation angles (ϕ; Fig. 4 a). The corresponding distribution of the x and y components of bacterial velocity along the top channel surface (v_x and v_y, respectively) was symmetric around zero, as expected. As the flow was gradually turned on, an asymmetry in velocity components began to emerge, together with a corresponding peak in ϕ (Fig. 4 b). In this mode, average bacterial migration was along the +x direction and upstream (+y direction), with the dominant body orientation just below 90° (measured relative to the +x direction). As shear flow was further increased, peak ϕ began to go down and the cells gradually turned more to face the +x direction as they were dragged with the flow (Fig. 4 c; see Fig. S1 in the Supporting Material for the entire data set of v_x, v_y, and ϕ distributions at all shear rates tested).

Figure 4.

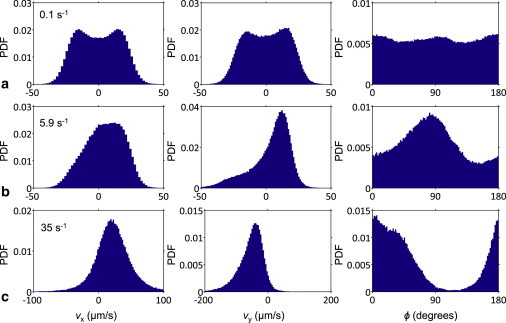
Three hydrodynamic modes of E. coli swimming over a surface. (a) Without flow, there is no net rheotaxis (i.e., v_x and v_y distributions are symmetric and zero mean) and all cell body orientation angles (ϕ) are equally likely. Here, we depict the PDFs for instantaneous v_x, v_y, and ϕ values at a shear rate just above 0 (∼0.1 s⁻¹) to elucidate the beginning of upstream orientation. (b) Positive rheotaxis is dominant up to a critical shear rate (6.4 s⁻¹), with the majority of the population swimming upstream (up to a mean v_y of 4 μm/s). Here, a peak in ϕ distribution just under 90° is clearly visible at a shear rate of 5.9 s⁻¹. (c) As the shear rate is increased beyond the critical, the bacteria begin to turn toward the +x axis and swim sideways as they get dragged by the flow. The ϕ peak correspondingly shifts to lower angles and approaches 0° with increasing flow. Here, the shear rate is 35 s⁻¹.

Stability of experimental conditions

Fig. 5 a depicts the distribution of swimming speeds (v) within the test population of E. coli under quiescent conditions, at both the beginning (μ = 22.3 μm/s, σ = 4.6 μm/s) and end of the experiment (>7 h long). Given the long extent of our experiment, it is interesting that the distribution of v remained the same. This is most likely because the cells were initially harvested from a dilution sample at the start of an exponential growth phase. Continuing their growth slowly at room temperature during the course of the experiments, E. coli did not reach saturation; hence, their population dynamics, including swim speed and cell size distribution (Fig. 5 b), remained constant. Therefore, we infer that no systematic bias is present in our data set regarding the composition of the bacteria population.

Figure 5.

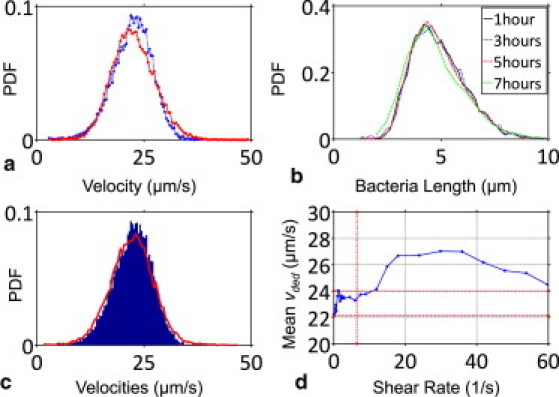
Evolution of E. coli hydrodynamic characteristics over the course of our experiment. (a) The (Gaussian) swim speed (v) distributions for the bacteria under no-flow conditions were virtually the same before (μ = 22.3 μm/s; σ = 4.6 μm/s; dashed curve) and after (μ = 22.5 μm/s; σ = 5.0 μm/s; solid curve) the experiment (>7 h long). (b) The PDF for cell length (log-normal; μ = 4.9 μm; σ = 1.3 μm) was also unchanged during this period. Results in A and B imply that the hydrodynamic characteristics of E. coli remained constant throughout the experiment. (c) The (Gaussian) PDF for deduced velocity (v_ded; μ = 22.2 μm/s; σ = 5.1 μm/s; solid curve) matches that for v (shown here for the beginning of the experiment; histogram) under quiescent conditions, as expected. (d) Variation of mean v_ded with shear rate. Each data point was extracted from the center location of a Gaussian fit to the distribution of v_ded at the given shear rate (representing thousands of bacteria trajectories). The 95% confidence interval in the mean location for each fit is typically below ±0.05 μm/s. The vertical dashed line depicts the critical shear rate (6.4 s⁻¹); the horizontal dashed lines mark v_ded extrema for shear rates below the critical.

When there is external flow present (in the y direction), one can use the swimming speed in the orthogonal direction (i.e., v_x) to infer the actual swim speed (i.e., v) of the bacteria, through

$$v_{ded}=\frac{v_x}{\cos \left(\varphi \right)}.$$ (1)

Using this approach, we deduced the swim speed distribution of E. coli in different shear rates. In this context, we first confirmed that the deduced swim speed (v_ded) under quiescent conditions replicated the tracked swim speeds (Fig. 5 c), as expected. With shear flow turned on, v_ded still remained normally distributed, although its mean exhibited slight variations (Fig. 5 d). Notice that each data point in Fig. 5 d corresponds to the average of thousands of v_ded values obtained from individual trajectories, and the uncertainty (i.e., 95% confidence interval) in the peak location of normally distributed deduced velocities was typically well below ±0.05 μm/s, making the variation observed in Fig. 5 d statistically significant. Interestingly, the average v_ded initially rose (up to 8%) with flow, stabilizing at ∼23.4 μm/s within the shear range 2–6 s⁻¹, and then continued to climb again until 29 s⁻¹. The reason for these higher average v_ded values is most likely the stabilizing effects of hydrodynamic alignment, which enables the cells to exit their occasional tumbles more rapidly. Beyond 29 s⁻¹, the average swim speed gradually went down with increasing shear rates, potentially due to increased hydrodynamic drag on the cell bodies as their downstream ends got pushed closer to the surface.

Emergence of positive rheotaxis

Fig. 6 summarizes the collective behavior of E. coli as a function of shear rate at the channel ceiling. As the dominant body orientation changed from facing upstream to facing sideways with increasing shear rate (Fig. 6 a), the average x velocity of the population gradually approached the average swim speed (Fig. 6 b). The emergence of a dominant ϕ was gradual with increasing shear (Fig. S1), because the initial appearance of flow-induced hydrodynamic effects on bacterial motility depended on individual body size and swim speed. At low shear rates, some cells still displayed random (i.e., tumbling), circular or loopy (13) trajectories, contributing basically a uniform background to the distribution of orientation angles. This was in addition to the normal distribution of ϕ (e.g., Fig. 4 b) that arose from other cells becoming hydrodynamically oriented to face upstream at the same shear rates. Hence, we determined the dominant angles depicted in Fig. 6 a by fitting a Gaussian plus a variable offset to orientation histograms of Fig. S1.

Figure 6.

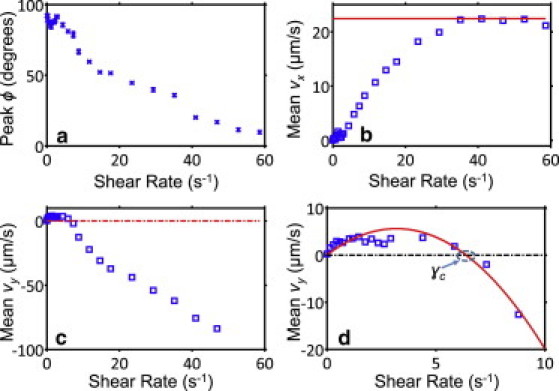
Peak orientation and average swim speed components of E. coli at various shear flows. (a) The peak in ϕ distribution remains at ∼90° until the critical shear rate (γ_c), beyond which the bacteria gradually turn sideways with increasing flow. (b) Mean v_x steadily increases with shear flow and saturates at the average swim speed of the overall observed cells (solid line), as expected. (c) On average, bacteria swim upstream for γ < γ_c and get dragged with faster flow. (d) We estimate the critical shear rate for any subpopulation of E. coli by fitting a second-order polynomial to the average v_y data in the vicinity of the transition from upstream swimming to downstream drag. Dashed lines in c and d indicate the point of zero net v_y.

We also noticed, especially at higher shear rates, that the weaker swimmers were increasingly overwhelmed by the fast shear flow, with their cell bodies rolling downstream and exhibiting closed, periodic and symmetric orbits around the x axis, with a mean ϕ = 0. We previously observed and characterized this particular phenomenon in a study involving nonflagellated E. coli in shear flow near a surface (19). The periodic orbits followed by these cell bodies are known as Jeffery orbits (named after the scientist who first showed mathematically that the angular motion of a prolate spheroid follows closed, kayak paddle-like orbits that depend on shear rate and particle aspect ratio (23)). In our analysis, we quantified the relative ratio of those cells to the rest of the population by adding a secondary, zero-mean Gaussian to the overall fit parameters for ϕ. This overall model (i.e., linear superposition of variable offset, variable-mean Gaussian, and zero-mean Gaussian fits to ϕ distribution data) captured E. coli behavior very well for all flow speeds (Fig. S1). The bacteria collectively displayed positive rheotaxis at low shear rates (Fig. 6 c), with the average v_y of the entire population (up to 4 μm/s) being positive up to 6.4 s⁻¹ (Fig. 6 d). We label the shear flow at which average v_y returns back to 0 (6.4 s⁻¹ for E. coli in this study) as the critical shear rate (γ_c). At faster shear rates, the bacteria were increasingly more likely to be dragged by flow, reverting to the regime described by Hill et al. (15).

Fig. 7 summarizes the relative abundance of three hydrodynamic mechanisms in the bacteria population: circular/random swimming (mode I; variable offset fit to ϕ data); flow-assisted orientation (modes II+III; variable-mean Gaussian in ϕ); and Jeffery orbits (zero-mean Gaussian fit to ϕ data) as a function of shear rate. The relative ratios of these three mechanisms were directly extracted from the simultaneous fits to each ϕ distribution in Fig. S1. Notice that increasing shear rates lead to a steady rise in hydrodynamic alignment within the population, whereas the incidence of circular/random swimming decreases. Interestingly, within the fit resolution, the critical shear rate also corresponds to a crossover between circular/random swimming and steady hydrodynamic alignment (Fig. 7). Furthermore, those cells that are overwhelmed by flow (exhibiting Jeffery orbits) become noticeable well below the critical shear.

Figure 7.

Relative ratios of circular/random swimmers (circles), hydrodynamically aligned bacteria (squares), and bacteria that display Jeffery orbits (triangles) as a function of shear rate. Hydrodynamic alignment steadily rises within the population with increasing shear rate, whereas the incidence of circular/random swimming decreases. Solid lines are fits that guide the eye; they bear a resemblance to first-order enzyme binding kinetics. For circular/random swimmers, ratio = 0.9/(1+(γ/7.2)^1.5); for hydrodynamically aligned cells, ratio = 0.7 × γ/(4.3 + γ); and for cells with Jeffery orbits, ratio = 0.5 × (γ − 2.9)/(17.1 + γ) for γ > 2.9.

Interestingly, even for shear rates substantially faster than 6.4 s⁻¹, we observed that the fastest swimmers could still overcome the flow and migrate upstream (e.g, see Fig. S1 b-23). We were able to manually track individual bacteria swimming directly upstream on the smooth, flat channel ceiling for millimeters at a time. If a swimmer got derailed after a tumble or collision with another bacterium, it would get dragged by the flow until it quickly found the surface again, become oriented to face the flow, and restart its upstream migration (Movie S2 in the Supporting Material).

Effects of bacterial parameters on positive rheotaxis

We analyzed γ_c and v_y within different subpopulations of E. coli in an attempt to determine the effect of bacterial parameters on positive rheotaxis. Fig. 8 a depicts the mean γ_c observed with various ranges of body length. Interestingly, whereas there is considerable variation in γ_c for individual bacteria within each subpopulation, the average values are close to constant across the spectrum. The reason for this is summarized in Fig. 8 b, which shows that the average swim speed (v_ded) was independent of cell length across all shear rates. This finding is intriguing because normally a longer cell body results in a higher hydrodynamic drag force on the bacterium while it swims. As such, it appears that longer bacteria, on average, are able to compensate for this increased drag through some mechanism. One possible hypothesis that is consistent with our data is that longer bacteria may, on average, possess more flagella (providing more propulsive power, and/or making the flagellar bundle stiffer with a smaller helical wavelength during swimming (24)), such that the average swim speed across different bacteria body lengths is the same. This hypothesis makes sense because longer cell bodies could support more peritrichous flagella on their surface, and the idea would be plausible if the added propulsive power from additional flagella could outpace any potential increase in friction losses within the flagellar bundle. This study provides no direct data to distinguish among various possible explanations for our observations, but we hope to examine this hypothesis experimentally in future work. One indirect prediction that arises from our hypothesis is that longer bacteria, on average, may tumble more often (assuming that reversal times of flagellar rotation direction are independent random variables). Such predictions of our hypothesis should be tested under stopped-flow conditions to eliminate the stabilizing effects of shear flow on bacterial orientations as they swim.

Figure 8.

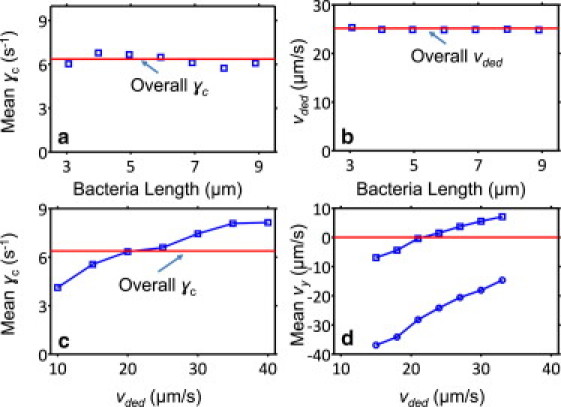
Relationships among γ_c, v_y, bacteria length, and deduced swim speed (v_ded). Swim rates and cell lengths are obtained from average values within each tracked bacterium trajectory. (a) γ_c as a function of cell length remains within ± 1 (s⁻¹) of the mean value for the entire population (6.4 s⁻¹). (b) Mean v_ded (at all shear rates) does not appear to change with bacteria length either, implying that longer cells, on average, may have more flagella that compensate for the increased hydrodynamic drag of their bodies. Solid lines in a and b indicate average values for γ_c and v_ded for the entire population, respectively. (c) γ_c is higher for faster bacteria, which are more likely to swim upstream at a given shear rate (d). Here, squares and circles stand for 5.9 s⁻¹ and 12 s⁻¹ shear, respectively, and the dotted line marks zero mean v_y.

On average, we observed that faster swimmers could continue to migrate upstream at higher shear rates (Fig. 8 c), and they tended to swim upstream faster at a given shear (Fig. 8 d), as expected.

Variation in upstream motility

The values of v_x, v_y, v_ded, and ϕ reported in Figs. 6 and 8 are all mean values within the corresponding subpopulations of E. coli. Each mean value depicted as a point in these figures was obtained from a distribution of these variables. Interestingly, there was substantial variation within each such distribution, and some individual fast swimmers migrated upstream much more quickly than the population average. For instance, even a group of E. coli swimming at a fixed shear rate with a fixed average v_ded had significant variation in their upstream motility, as illustrated in Fig. 9 for a shear rate of 2.9 s⁻¹ and v_ded = 24 μm/s (range: 22.5–25.5 μm/s). Of note, 7.2% of the cells in this case migrated upstream faster than 20 μm/s, even though the subpopulation average v_y was only 2.4 μm/s.

Figure 9.

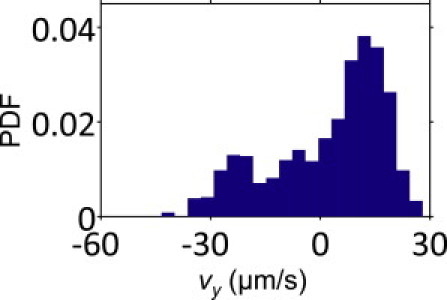
Distribution of v_y among a subpopulation of 1035 bacteria that swim at 24 μm/s (deduced) on average (range: 22.5–25.5 μm/s) at a shear rate of 2.9 s⁻¹. While the mean v_y is 2.4 μm/s, 7.2% of the cells swim upstream much faster (> 20 μm/s). Others get dragged downstream, either because they happen to face away from the +y direction as they swim on the surface, or simply because they are somewhat farther away from the surface itself and the local flow they experience is faster.

Discussion

A hydrodynamic perspective

The tendency of E. coli to swim into the surface has been elucidated in many recent publications, including a study by Lauga et al. (11). Specifically, Eq. 19a of that work shows that the axial torque on the cell will be negative, meaning that the bacterium will tend to dip toward the surface as it swims over it. It also shows that this torque will be proportional in part to ω, the rate of flagellar rotation. However, the proportionality is not physically due to flagellar rotation directly, but to the linear motion of the cell that the flagella drive. This is clear from the second line of the matrix in Eq. 9 of the same reference. Here, the linear propulsive force (F_y) depends in part on the flagellar rotation rate ω through

$$F_y\sim -M_{yy}^{F\Omega }\left({\Omega }_y-\omega \right)+\dots .$$ (2)

With the cell body rotation (Ω_y) taken to be much slower than flagellar rotation (i.e., Ω_y « ω), it becomes the flagellar rotation rate that determines the linear propulsive force (and the eventual steady-state cell velocity U_y (see also Eq. 14a in Lauga et al. (11)) through the cell body mobility term $M_{yy}^{F\Omega }$. Hence, in Eq. 19a of Lauga et al. (11), it is the physical forward motion of the cell (as determined by the $M_{yy}^{F\Omega }\omega$ term) that causes it to dip forward as it swims just over a surface.

As long as a microorganism swims freely over a surface (without relying on attachment or physical contact with it), the increased hydrodynamic drag ($V_{xy}^{\mathit{LU}}$ in Eq. 8 of Lauga et al. (11)) on the cell body will cause a torque (L_x) that dips the front of the cell toward that surface. In that regard, the microorganism could be using helical flagella (as in E. coli), a whip-like tail (as in a human sperm), or undulating microcilia (as in Paramecium) to propel itself over, and the forward dip toward the surface is still likely to happen. Obviously, we did not get to test other cells in this study, but the physical insights that we gain by studying E. coli in shear flow, together with what we already know about the hydrodynamics of bacterial motility, allow us to reach this conjecture.

Estimation of the dip angle in the absence of flow

Equation 20 of Lauga et al. (11) compares the rotational speed of a bacterium body along the lateral axis (i.e., the rate of dipping toward the nearby surface) with its forward swim velocity. Specifically, it is found that the rotation speed at the surface of the cell body is much smaller than swim speed (i.e., aΩ_x « U_y, where a denotes the average hydrodynamic radius of the cell body). This is a fair assessment that we agree with, but it does not necessarily mean that the bacterium does not have enough time to reach a steady-state angle with the surface along the x direction. We conjecture that, given a swim speed and cell body length, a bacterium swimming freely over a surface in the absence of flow must reach a shallow but finite (i.e., nonzero) steady-state angle along the x direction. Of course, due to Brownian motion and other disturbances (collisions with other bacteria, cell tumbling, etc.), this steady-state angle would be a time-average value.

We believe that this steady-state angle is likely to be small, for various reasons. First, there is no discernible focus difference between the front and the back of even the longest cells swimming under our microscope over a surface, even when using a 40× objective with a 2 μm depth of field. Also, we do not observe any apparent changes in cell length if the bacterium body suddenly attaches to the glass microscope slide. Finally, any large dip angle would create a substantial hydrodynamic resistance torque on the cell body flagella complex, which would quickly tend to dip its back toward the surface.

Based on these observations, we expect that the steady-state angle along the axial (x) direction will be on the order of ≤5°. We can obtain a good estimate for this angle using the same linear viscous drag theory developed by Lauga et al. (11). Specifically, we can derive an expression for this angle (α) by balancing the torque that tends to dip the cell front toward the surface (L_f in Fig. 10) with the restoring torque that arises due to the hydrodynamic drag force (F_f) on the flagellar bundle.

Figure 10.

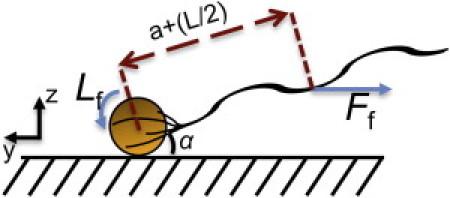
Steady-state lateral angle (α) can be estimated by balancing the –x directed torque (L_f) on the cell body that arises from increased drag over the surface with the hydrodynamic torque that tends to orient the cell parallel to the surface as it swims.

The expression for L_f can be found using the expression for the coupling coefficient between forward cell velocity and L_f in Eq. 26e of Lauga et al. (11):

$$\left|L_f\right|\approx V_{xy}^{LU}{U}_y\approx 8\pi \mu a^2\left[\frac{1}{10}\ln \left(\frac{a}{h}\right)-0.19\right]U_y.$$ (3)

The hydrodynamic drag force on the flagellar bundle is approximately uniform while the bacterium swims forward in the absence of flow. The total drag force acts over an average lever arm given by the cell body radius (a) plus half the length of the flagellar bundle (i.e., L/2). The component of F_f that tends to rotate the cell is F_f sin(α) and can be derived from the expression for vertical force on the helical bundle using Eq. 28a of Lauga et al. (11):

$$L_{res}=F_f\sin \left(\alpha \right)\left(a+\frac{L}{2}\right)=2c_{\parallel }L\frac{1+3{\epsilon }^2/4}{{\left(1+{\epsilon }^2\right)}^{1/2}}\sin \left(\alpha \right)\left(a+\frac{L}{2}\right)U_y.$$ (4)

Here, c_‖ is the tangential drag coefficient on each small segment of the helical bundle (approximated as a slender body) and ε = 2πb/λ, where b is the helix radius and λ is the helix wavelength. Following the conventions in Lauga et al. (11) (for ease of model comparison), we will take a = 1 μm (medium value from the fits in that reference), b = 250 nm, λ = 2.5 μm, and L = 7.5 μm. The drag coefficient c_‖ can be computed using slender body theory, as is done in Eq. 6 of Lauga et al. (11):

$$c_{\parallel }=\frac{2\pi \mu }{\ln \left(2\lambda /r\right)-0.5},$$ (5)

where r is the radius (half-thickness) of the flagellar bundle itself. Following Lauga et al. (11), we will take this value to be 50 nm.

Equating Eq. 2 to Eq. 3 above, we can solve for the equilibrium value of α. Note that in this process, the variable for forward cell velocity cancels out and α becomes independent of cell velocity:

$$\alpha ={\sin }^{-1}\left(\frac{2c_{\parallel }L\frac{1+3{\epsilon }^2/4}{{\left(1+{\epsilon }^2\right)}^{1/2}}\left(a+L/2\right)}{8\pi \mu a^2\left[\frac{1}{10}\ln \left(\frac{a}{h}\right)-0.19\right]}\right).$$ (6)

For all the values listed above, we find that α is ∼3°. This value is in perfect agreement with our expectations. Notice that treating the cell body as a sphere neglects the fact that the actual, elongated E. coli body shape will contribute to the hydrodynamic restoring force that tends to flatten its orientation angle. Therefore, we believe the actual value of α should be somewhat smaller than 3°.

The finite, positive value of α found in this simple theoretical treatment supports our conjecture that the bacteria maintain a steady-state dip angle toward the surface on which they swim.

Timescale for dipping

The timescale in which the cell body dips 3° toward the nearby surface from an initial horizontal position can be estimated by using the same analysis conducted by Lauga et al. (11). Using their Eq. 20 for shallow angles, we find that the angular rotation rate for dipping can be approximated as

$${\Omega }_x\approx \frac{1}{a}{\left(\frac{a}{L_{\parallel }}\right)}^3{U}_y.$$ (7)

Assuming an average swim speed of 22.5 μm/s (from our bacteria population), the time it takes for the cell body to rotate 3° is

$$\Delta t=\frac{3°\left(\pi /180\right)}{{\Omega }_x}\approx 0.98\mathrm{s}.$$ (8)

This timescale is comparable to or less than the average period between consecutive tumbles for E. coli (25); hence, the bacteria should typically have enough time to reach steady state dipping angle before tumbles. We suspect that the actual timescale might be even shorter, because in our experiments we observed that upstream swimming E. coli that collided with other cells would recover their upstream orientation and resume their migration in well less than a second.

Estimating shear flow modifications

The presence of shear flow creates an additional drag force on the cell body and flagella. Without any modifications to the calculations in Lauga et al. (11), one would normally expect this phenomenon to manifest itself as a negative (i.e., downstream-oriented) offset in cell velocity. Experimentally, however, we observe a systematic orientation of the cell body to face upstream and even direct upstream migration in the presence of shear flow. This behavior that we discuss here cannot be explained by the assumptions of Lauga et al. (11), because with α = 0 there can be no cellular orientation in shear flow.

It is possible, however, to apply the more generalized calculations in Lauga et al. (11) to determine the effect of shear flow on cellular swimming near a surface, following in the footsteps of what we demonstrated above to calculate α. Specifically, it is possible to go beyond the calculations in Lauga et al. (11) to show how shear flow also tends to rotate the bacterium to face upstream. An effort to demonstrate this agreement between linear hydrodynamic theory and our experiments is in progress. However, it is possible to combine our experimental results with the calculations presented so far to offer a deeper understanding of the hydrodynamics of bacterial swimming near surfaces.

Overall picture

A more complete picture of bacterial motility emerges from this study in the light of previous work. In the case of E. coli, it is known that flagellar rotation, together with the counter-rotation of the cell body over the surface, result in circular swimming under quiescent conditions (mode I) (11,26). In this mode, increased hydrodynamic drag between the cell and the surface rotates and dips the front of the body, keeping the bacterium continuously pointed toward the surface and swimming over it for extended periods (11). Interestingly, the presence of this dip angle is not a consequence of the particular morphology and nature of the flagellar bundle, but of the microorganism's forward motion over the surface. The front of the cell body is closer to the surface and experiences a larger hydrodynamic resistance to motion compared with its back. In the presence of moderate flow (mode II), the back of the cell drags downstream more easily, resulting in the cell rotating to face directly upstream. This hydrodynamic torque on the bacterium body provides a stabilizing influence on cell orientation against rotational Brownian motion and even cell tumbling (once a cell exits a tumble, it quickly starts swimming upstream again). We conjecture that faster shear rates push the back of the bacterium and its flagellar bundle closer to the bounding surface, increasing the tendency for circular swimming. The dynamic equilibrium for bacterial orientation gradually shifts toward more acute angles with higher flows (Fig. 6 a) and soon the bacteria begin to migrate sideways as they get dragged with flow (mode III). In this hydrodynamic regime, the cells continuously swim in the +x direction to get out of the high-shear flow region. Once clear, the bacteria can then resume swimming upstream, either directly on a flat surface (positive rheotaxis) or within trenches, microcracks, and next to sidewalls, as described previously (15).

Significance and relevance of findings

When surface roughness and bacterial adhesion are factored out, upstream motility in E. coli appears to be mainly determined by the local shear rate. Hence, we deduce that flow-assisted upstream migration in E. coli must be a ubiquitous phenomenon within all bounded, locally laminar flows found in nature or in man-made structures. As long as the bounding surface is locally or piecewise smooth and sustains a laminar flow within the first few microns over its surface, it will support positive rheotaxis in E. coli. Any imperfections, cracks, scratches, or sidewalls within the bounding surface will provide relief from high-shear flow regions and also lead to upstream motility. Therefore, the findings reported here may be relevant for irrigation channels, riverbeds, underground water streams, wastewater treatment facilities, house and city plumbing, and medical catheters that support continuous or intermittent flow (e.g., urinary catheters). Bacteria entering such flow systems at a downstream location could be capable of migrating upstream much faster than a gradually advancing biofilm. For instance, a silicone Foley catheter with an average internal lumen diameter of 4.4 mm inside an otherwise healthy adult urinary tract (producing an average of 60 ml/h of urine (27), depending on fluid intake) is subject to a maximum shear rate of 2.9 s⁻¹. Bacteria swimming at 24 μm/s at this shear rate could have an upstream travel rate of 20 μm/s (Fig. 9) and would traverse the entire length of a 30 cm Foley catheter in <5 h. Even neglecting potential back flow and biofilm issues, the catheterized bladder is bound to be colonized very rapidly.

Conclusion

From our findings regarding the hydrodynamics of flow-assisted upstream migration, we draw two conclusions: First, it may be possible to substantially delay bacterial pathogenesis in flow systems such as catheters without resorting to antimicrobial chemicals that inevitably lead to the emergence of resistant strains. Specifically, incorporating suitably chosen hydrodynamic barriers could locally raise shear rates substantially above γ_c for the fastest swimmers to stop flow-assisted upstream motility. Although it may not necessarily stop an encroaching biofilm, this approach could render short-term catheterization practical. Second, the hydrodynamics of positive rheotaxis simply requires a microorganism freely swimming over a surface in moderate flow and is not unique to the propulsion mechanics of E. coli. As such, we predict that it may be quite ubiquitous in the world of microscopic free swimmers.