Energy Landscapes of Dynamic Ensembles of Rolling Triplet Repeat Bulge Loops: Implications for DNA Expansion Associated with Disease States

Abstract

DNA repeat domains can form ensembles of canonical and noncanonical states, including stable and metastable DNA secondary structures. Such sequence-induced structural diversity creates complex conformational landscapes for DNA processing pathways, including those triplet expansion events that accompany replication, recombination, and/or repair. Here we demonstrate further levels of conformational complexity within repeat domains. Specifically, we show that bulge loop structures within an extended repeat domain can form dynamic ensembles containing a distribution of loop positions, thereby yielding families of positional loop isomers, which we designate as “rollamers”. Our fluorescence, absorbance, and calorimetric data are consistent with loop migration/translocation between sites within the repeat domain (“rollamerization”). We demonstrate that such “rollameric” migration of bulge loops within repeat sequences can invade and disrupt previously formed base-paired domains via an isoenthalpic, entropy-driven process. We further demonstrate that destabilizing abasic lesions alter the loop distributions so as to favor “rollamers” with the lesion positioned at the duplex/loop junction, sites where the flexibility of the abasic “universal hinge” relaxes unfavorable interactions and/or facilitates topological accommodation. Another strategic siting of an abasic site induces directed loop migration toward denaturing domains, a phenomenon that merges destabilizing domains. In the aggregate, our data reveal that dynamic ensembles within repeat domains profoundly impact the overall energetics of such DNA constructs as well as the distribution of states by which they denature/renature. These static and dynamic influences within triplet repeat domains expand the conformational space available for selection and targeting by the DNA processing machinery. We propose that such dynamic ensembles and their associated impact on DNA properties influence pathways that lead to DNA expansion.

Introduction

Genome sequencing and mapping projects have revealed the genome to be quite dynamic, with DNA-altering expansion and deletion events exhibiting enhanced frequency within repetitive sequence domains.¹⁻⁷ For example, stretches of trinucleotide repeat sequences represented by (CNG)_n (where N = A, T, or C) exhibit higher probabilities for expansion when a threshold number of repeats (n ≥ 35) is exceeded.^5,7−9 Intriguingly, DNA expansion and deletion events occur with greater frequency during DNA replication,¹⁰⁻¹³ DNA recombination,¹⁴⁻¹⁷ and/or DNA repair^4,18,19 [especially base excision repair (BER)²⁰ and mismatch repair (MMR)^21,22], although the pathways that couple these events remain unknown. What is known, however, is that triplet repeat genomic expansion events yield genotypes that correlate with the phenotypes associated with a myriad of human diseases and developmental disorders, including Huntington’s (the CAG repeat²³) and myotonic dystrophy type 1 (DM1) (the CTG repeat²⁴). Currently, there are over 30 known diseases that can be traced to expansion events in CNG repeats.²⁵⁻²⁸

The propensity of repeat domains to adopt slipped-out (meta)stable bulge loop secondary structures is believed to influence the processes that lead to DNA expansion and ultimately to the disease state.^6,9,29−33 We have shown³⁴ that once formed, such metastable triplet repeat bulge loop structures do not spontaneously rearrange to their more stable duplex form unless there is sufficient energy to overcome the activation barriers that protect these kinetically trapped secondary structures (Scheme 1A). We also have demonstrated³⁵ that within extended repeat domains, these metastable structures are composed of ensembles of closely related microstates (represented in Scheme 1A by the fine structure within the energy well of the loop) that collectively constitute the triplet repeat bulged looped macrostate. Such ensembles of closely related repeat DNA secondary structures could trap and misdirect the normal cellular DNA processing machinery into erroneously copying the repeat sequence, thereby leading to DNA expansion. Recently, McMurray and co-workers presented evidence in support of this view by demonstrating the irreversible trapping of the MSH2–MSH3 mismatch repair complex in nonfunctional states by multiple CAG repeat bulge loop conformations.³⁶ These authors have also argued that repeat loop conformation and dynamics, including the dynamics of junctions between repeat loop and adjacent DNA domains, are important in mismatch-repair-induced expansion/deletion events.

Scheme 1A. Schematic of the Relative Free Energy Profile of a Positionally Fixed (“Static”) Metastable Triplet Repeat Bulge Loop Structure.

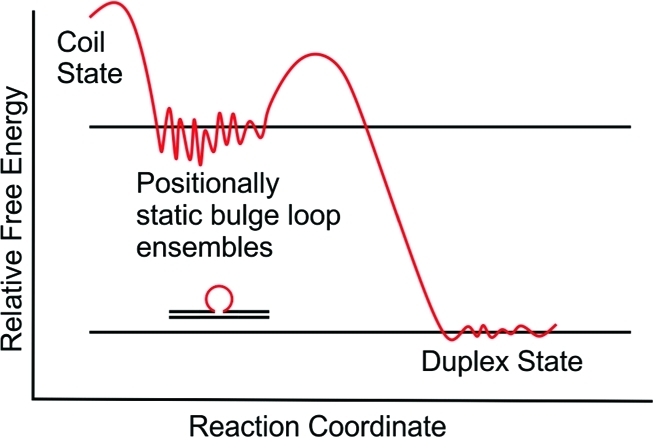
The ensemble of bulge loop microstates that constitute the repeat bulge macrostate³⁵ is conceptually represented by the fine structure drawn in the repeat loop energy well.

To date, most in vitro investigations have focused on models with static ensembles comprising the entire repeat domain by itself³⁷⁻⁴⁵ or partitioned into the bulge loop complex.^34,46−50 However, in vivo it is likely that only a (small) part of the larger repetitive domain adopts the slipped-out bulge loop secondary structure assumed to be responsible for DNA expansion, while repetitive sequence domains on either side of the looped-out region remain in a duplex state.⁵¹⁻⁵³ In such a scenario, the bulged-out repeat domain may be located in one of several energetically equivalent positions relative to nonrepetitive upstream and downstream sequences, as illustrated in Scheme 1B. We designate these positional isomers as ”rollamers”. Such a statistical distribution of loop positions reflects a (Boltzman) entropy contribution favoring the loop occupying multiple degenerate/equivalent positions within an extended repeat domain.⁵⁴

Scheme 1B. Schematic of the Relative Free Energy Profile of “Static” Metastable Triplet Repeat Bulge Loops in Multiple Equivalent Loop Positions.

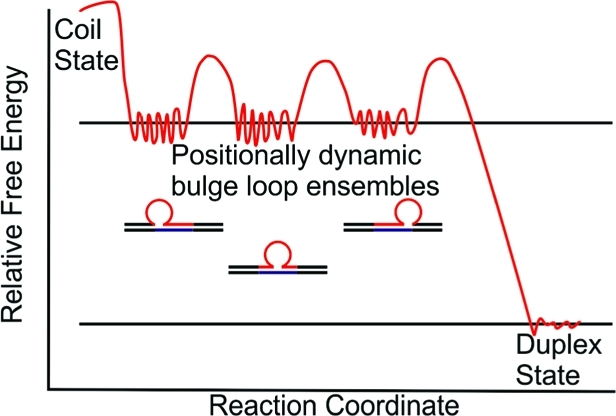
The ensemble of bulge loop microstates that constitute the macrostate of each positional loop isomer is indicated by the fine structure in the repeat loop energy wells.

Within such extended repeat sequence domains, the intriguing possibility of loop migration (“rollamerization”) between such formally “static” positional loop isomers exists, specifically when base-paired repeat sequences are positioned on either side of a repetitive bulge loop structure. This unique dynamic feature expands the conformational space that challenges and/or facilitates the selective processing of such biologically relevant repeat domains. In this “rolling loop” migration model (stylized in Scheme 1C), an equal number of base pairs are broken and formed upstream and downstream of the repeat loop, thereby making the net migration process enthalpically neutral.

Scheme 1C. Schematic of the Relative Free Energy Profile of a Metastable Dynamic Triplet Repeat Bulge Loop (“Rollamer”) in Multiple Positions.

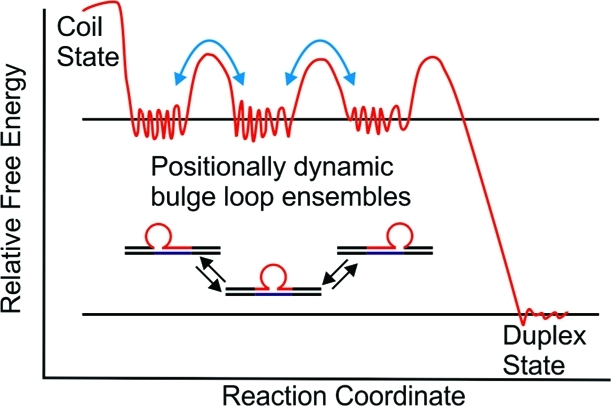
The dynamic interchange between loop isomers (“rollamerization”) is indicated by the equilibrium arrows. The light-blue arrows linking different repeat loop energy wells indicate the activation energy barriers for dynamic interchange between different positional loop isomers via loop migration.

In this rollamer model, there is a requirement that base pairs ahead of and secondary structure elements within the migrating loop domain be at least transiently disrupted. This feature results in activation barriers that temper the interconversion of the positional isomers. Consequently, in the absence of sufficient energy input (kinetic control), the positional loop isomers are at least transiently stable (metastable). In other words, the conventionally studied static ensemble of closely related repeat loop structures (positional isomers) has the capacity, within larger repeat sequence domains, to become a dynamic ensemble via loop migration. Such a dynamic repeat loop secondary structure ensemble would provide additional challenges to the DNA replication, recombination, and repair machinery, thereby contributing to the processes leading to DNA expansion.

Motivated by the possibility of regulation of DNA processing and misprocessing pathways via conformational selection, we report here on the unique properties and energy landscapes of dynamic triplet repeat loop ensembles. To this end, we designed an oligonucleotide model system based on the previously described Ω-DNA construct^34,48,55,56 that allows for loop migration. We strategically incorporated structure-sensitive fluorescent nucleobase analogues and selectively monitored loop variants to assess the degree of loop distribution and migration. On the basis of thermodynamic and spectroscopic evidence, we show that repeat bulge loops are distributed in multiple positions within a larger repetitive domain and that loop migration between such loop positions can occur. We also present evidence that in the dynamic systems described here, higher-order structure formation (in this case loops) can disrupt preformed base-paired DNA domains. We discuss potential implications of our observations for biological processes involved in repeat DNA expansion events.

Materials and Methods

Materials

Oligonucleotides were synthesized on a 10 μmol scale by standard phosphoramidite chemistry using an Äkta DNA synthesizer and purified by 4,4'-dimethoxytrityl (DMT)-on and subsequent repeated DMT-off reversed-phase HPLC, as described previously.^46,57−59 The oligonucleotides were assessed for purity by analytical HPLC and ion-spray mass spectrometry and found to be pure by analytical HPLC and better than 98% pure by mass spectrometry. The purified oligonucleotides were dialyzed using dispo-dialyzers with a molecular weight cutoff of 500 Da (Spectrum, Rancho Dominguez, CA) against at least two changes of pH 6.8 buffer containing 10 mM cacodylic acid/sodium cacodylate and 0.1 mM Na₂EDTA along with sufficient NaCl to yield a final Na⁺concentration of 100 mM. DNA extinction coefficients (λ = 260 nm) of the parent sequences lacking repeats ([CAG]₀, [CTG]₀) were determined by phosphate assay under denaturing conditions^60,61 (90 °C) and were found to be ε_[CAG]0 = 190 400 M^–1 cm^–1 and ε_[CTG]0 = 186 200 M^–1 cm^–1. For all other oligonucleotides, extinction coefficients (260 nm, 90 °C) were determined from continuous variation titrations (Job plots) with the complementary parent oligonucleotide and found to be ε_[CAG]2 = 251 400 M^–1 cm^–1, ε_[CAG]4 = 315 500 M^–1 cm^–1, ε_[CAG]6 = 368400 M^–1 cm^–1, ε_[CAG]8 = 424 900 M^–1 cm^–1, ε_[CTG]2 = 221 700 M^–1 cm^–1, ε_[CTG]4 = 271 100 M^–1 cm^–1, ε_[CTG]6 = 342 900 M^–1 cm^–1, and ε_[CTG]8 = 380 500 M^–1 cm^–1. The extinction coefficient of the [CAG]₈ repeat containing the fluorescent base analogues 2-aminopurine (2Ap) and pyrollocytosine (PC) was found to be ε_{[CAG]8–2ApPC} = 427 300 M^–1 cm^–1, while the introduction of a tetrahydrofuranyl (THF) abasic site in place of guanidine resulted in a extinction coefficient of ε_{[CAG]8–2ApPC–F} = 420 000 M^–1 cm^–1.

DSC Studies

Differential scanning calorimetry (DSC) studies were conducted using a NanoDSCII differential scanning calorimeter (Calorimetry Science Corporation, Lindon, UT) with a nominal cell volume of 0.3 mL as described previously.^34,48,62 Oligonucleotides, at a concentration of 50 μM in strand, were repeatedly scanned between 0 °C and 90 or 95 °C at a constant heating rate of 1 °C/min while the excess power required to maintain the sample and reference cells at the same temperature was continuously recorded. After conversion of the measured excess power values to heat capacity units and subtractions of buffer-versus-buffer scans, the raw DSC traces were normalized for DNA concentration and analyzed using Origin software. The calorimetric enthalpy (ΔH_cal) was derived by integration of the excess heat capacity (<C_p>) curve, and ΔC_p was derived from the difference in the linearly extrapolated pre- and post-transition baselines at T_m. ΔS was derived as ΔH/T_m, assuming “pseudomonomolecular” behavior in which propagation dominates initiation.^63,64T_m is defined as the temperature at the midpoint of the integrated excess heat capacity curve for a given conformational transition, which corresponds to half the sample being denatured for a process that exhibits pseudomonomolecularity. We fit the experimental excess heat capacity curves of our Ω-DNA’s to a model for two independent two-state transitions as described previously.^{48,55,56,65,66} We found that we could obtain good agreement between the experimental curves and the fitted curves for all of the Ω-DNA constructs with the repeat loop in a fixed position, but we failed to obtain good fits for those constructs where the repeat loop can be located in multiple positions.

CD Studies

Circular dichroism (CD) spectra as a function of temperature were recorded using an AVIV model 400 spectropolarimeter (Aviv Biomedical, Lakewood, NJ). Spectra were recorded with an averaging time of 10 s using either a 10 mm cell (420–290 nm) or a 1 mm cell (420 and 205 nm) in steps of 1 nm between 0 and 95 °C in 5 °C intervals. After subtraction of the relevant buffer scans, spectra were normalized for DNA concentration as previously described^34,57 and analyzed further. The oligonucleotide concentrations were 10 μM in strand.

UV Absorption Studies

UV spectra and temperature-dependent changes in UV absorbance were measured using an AVIV model 14 UV/vis spectrophotometer (Aviv Biomedical, Lakewood, NJ). Temperature dependent changes in UV absorbance at 260 nm with a 1 nm bandwidth were recorded with an averaging time of 5 s while the temperature was raised in steps of 0.5 °C with 1 min equilibration time. Olignucleotide concentrations were 1.5 or 2 μM in strand.

Fluorescence Studies

Fluorescence spectra and temperature-dependent changes in fluorescence intensity were measured using a Varian Eclipse spectrofluorimeter. Fluorescence spectra between 320 nm (350 nm) and 600 nm were recorded with excitation at 305 nm (for 2Ap and PC) or 340 nm (for PC) using a 5 nm excitation slit width, a 10 nm emission slit width, and a photomultiplier setting of 800 V. The oligonucleotide concentrations were 2 μM in strand in a 1 cm fluorescence cuvette. Temperature-dependent changes in fluorescence intensity were monitored either by exciting 2Ap at 305 nm and recording changes at 370 nm (the 2Ap emission maximum) or 460 nm (the PC emission maximum) or by exciting PC at 340 nm and monitoring the PC emission at 460 nm using the same settings.

Results and Discussion

The System: Positional Isomers of Triplet Repeat Loops

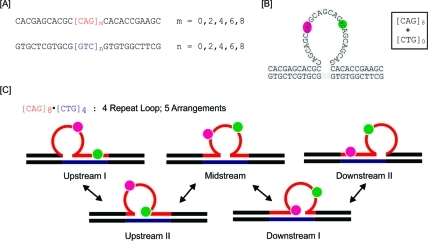
To assess the impact of triplet repeat bulge loops in multiple arrangements of positional isomers (rollamers) and the potential migrations between these states (rollamerization), we devised the model system depicted in Scheme 2. As shown in Scheme 2A, we hybridized oligonucleotides with a fixed number m of CAG repeats (m = 0, 2, 4, 6, 8) inserted between nonrepeat domains of 11 bases upstream and downstream with oligonucleotides containing the corresponding complementary 11 bases upstream and downstream of a fixed number n of CTG repeats (n = 0, 2, 4, 6, 8). This hybridization yields a triplet repeat bulged loop structure flanked by 5′ and 3′ duplex domains, as illustrated in Scheme 2B. We previously showed that annealing of such oligomers with either m = 6, n = 0 or m = 0, n = 6 results in the formation of a stable repeat bulge loop ensemble in a fixed/“frozen” position relative to the upstream and downstream duplex arms.^34,48 It should be noted that when m > n ≠ 0, a bulge loop construct with a CAG repeat loop of size m – n results, with n additional base-paired CAG/CTG triplets distributed between the upstream and/or downstream duplex domains. Significantly, this loop and the n extra base-paired CAG/CTG triplets can assume n + 1 possible arrangements within the repeat domain, so a unique position for a single loop is not defined. Conversely, when n > m ≠ 0, one obtains a bulge loop construct with a CTG repeat loop of size n – m in m + 1 possible arrangements along with m additional base-paired CAG/CTG triplets. Implicit in these expectations is the assumption that a CNG triplet in its entirety is either part of the loop or part of one of the duplex domains (upstream or downstream), a reasonable assumption since otherwise too many intraloop contacts would be disrupted. In short, the loop positions differ in steps of three bases/base pairs, as further underscored in the Supporting Information.

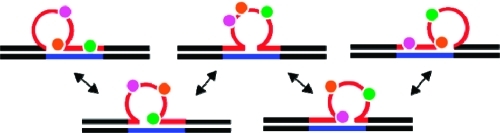
Scheme 2. (A) Oligonucleotide Variants Used in This Study; (B) Schematic of the “Static” Repeat Bulge Loop Construct Formed by Combining Oligomers [CAG]₈ with [CTG]₀ (an Eight-CAG Repeat Bulge Loop in One Fixed Arrangement); (C) Schematic of the Different Positional Loop Isomers for Loops That Can Exist in Five Equivalent Loop Arrangements, Here Represented by [CAG]₈·[CTG]₄.

In panel (B), the repeats where an adenine is replaced by 2-aminopurine (2Ap) and a cytosine by pyrollocytosine (PC) in the fluorescently labeled constructs are indicated in pink and green, respectively. In panel (C), the positions of the fluorescent labels and their partitioning in different structural domains for the different rollamers are shown.

Given the repetitive nature of the base-paired sequence upstream and/or downstream when m ≠ n ≠ 0, the junctions between the bulge loop and the duplex domains in each potential arrangement are identical, and barring end effects, all of the potential positions indicated schematically in Scheme 2C are equally likely. Here we report the results on repeats where m and n are even numbers, as previous studies have suggested an even/odd effect on the thermal and thermodynamic properties of (fixed) CAG/CTG repeats due to differences in the alignment of repeats in the loop domain.^67,68 We focus our discussion primarily on the [CAG]₈·[CTG]₄ construct, in which a four-CAG repeat loop can assume five possible loop arrangements/isomers, as this construct most clearly displays the features of dynamic repeat loops in multiple states. As needed, to clarify specific points, we will refer to data we collected on other [CAG]_m·[CTG]_n (m, n = 0, 2, 4, 6, 8) and related constructs.

The Potential of a Triplet Repeat Loop To Occupy Multiple Positions Alters the Melting Behavior

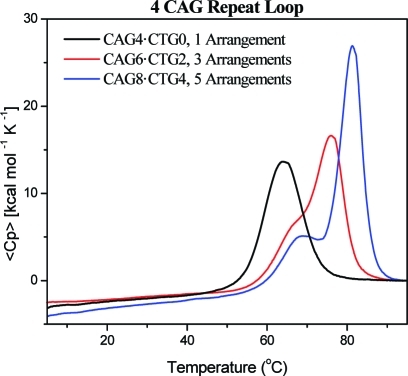
Figure 1 shows typical DSC thermograms obtained for a bulge loop oligonucleotide comprising four CAG repeats in either a fixed loop position (black trace) or a distribution of three (red trace) or five (blue trace) potential loop positions. Whereas the repeat loop in a fixed position gives rise to a single cooperative melting transition, as described previously,^34,48 the possibility probed here for the repeat loop to occupy multiple positions results in more complex melting curves, yielding two visually resolved, overlapping transitions. As the number of possible loop positions increases, these two transitions become more resolved while shifting progressively to higher temperatures and manifesting higher melting enthalpies. This observed split into two melting transitions is of particular interest. If the loop occupies a fixed position, simply extending the upstream and downstream duplex arms by an additional 3n base pairs should maintain a single transition, albeit a more cooperative one with a higher enthalpy and a higher T_m. In contrast, we observed two transitions that became better resolved with increasing chain length. This experimental reality suggests that the bulge loop is located, either statically or dynamically, in multiple positions relative to the upstream and downstream arms and that interchangeability within the distribution alters the melting behavior of these constructs relative to equivalent loops in “frozen” constructs that limit the loop to a single fixed position. The complementary fluorescence, absorption, and calorimetric data described below are consistent with such a rollamer model.

Figure 1.

Excess heat capacity curves measured for a repeat loop construct composed of four CAG repeats located in a fixed position (black) or distributed between three (red) or five (blue) equivalent loop positions. Similar results were obtained for different CAG loop sizes and for CTG repeat loops in multiple equivalent loop positions.

Enthalpic Discrimination between Constructs with Repeat Loops in Multiple Equivalent Positions versus a Singular Fixed Loop Position

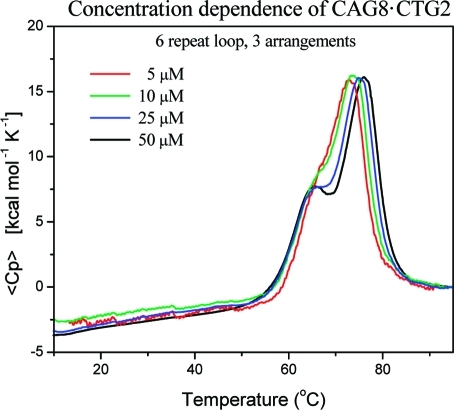
Intriguingly, we found that the enthalpy changes of the resolved peaks scale roughly with the number of possible loop arrangements (i.e., 1:2 for three arrangements or 1:4 for five arrangements), while the increase in the total enthalpy change relative to the fixed loop position is consistent with that expected for bulge loop DNAs with a corresponding number of additional base pairs in the upstream/downstream duplex domain. These observations initially suggested that one could resolve the ensemble of different loop positions on the basis of their differences in melting temperature. However, our subsequent studies with different repeat loop sizes and studies with CTG instead of CAG repeats revealed that differences in loop size or sequence are reflected exclusively in the T_m and enthalpy change of the first transition. The second transition depends only on the number of possible loop arrangements within the construct, regardless of the loop size or loop sequence. Furthermore, the concentration-dependent studies shown in Figure 2 revealed the lower transition to be independent of DNA concentration, reflective of a monomolecular transition, whereas the upper transition is DNA-concentration-dependent, consistent with a bimolecular process. Collectively, these results are consistent with only the upper transition involving complete strand separation. Thus, one cannot yet conclude whether the apparent scaling of the DSC peaks with different populations of potential loop arrangements within the ensemble reflects a fundamental relationship. Significantly, however, such a determination is not required for the analysis and interpretation of the data presented here.

Figure 2.

Excess heat capacity curve showing the concentration dependence of conformational transitions of [CAG]₈·[CTG]₂, a six-CAG repeat loop that can form in three loop positions. The concentration-dependent change in the upper transition should be noted.

Taken together, our observations are consistent with models in which the first melting transition involves some partial melting and/or rearrangement of the molecule as a whole, while the second transition reflects denaturation of the residual structure and strand separation as opposed to melting of the individual components of the overall ensemble at different temperatures. This interpretation is supported by the fact that the shapes of the experimental DSC curves cannot be fit using two independent two-state transitions, because the first resolved transition is not two-state in nature.

The All-T-Loop Control

To understand why the single transition observed for a triplet repeat fixed loop splits into two transitions when the same loop can be arranged in multiple positions within the repeat domain, we investigated the melting of constructs with putatively unstructured all-T loops “frozen” in fixed positions. This system was formed by selective placement of base-paired CAG/CTG triplets in the upstream or downstream arms based on the [CAG]₈·[CTG]₄ construct, as shown in Scheme 3.

Scheme 3. Schematic Representation of the All-T Repeat Loop Constructs “Frozen” in Fixed Positions: Placement of the Base-Paired CAG/CTG Domain, Indicated by Red Letters, “Freezes” the All-T Loop Relative to the Upstream and/or Downstream Nonrepetitive 11-mer Arms.

We found that only when the all-T loop is fixed in the downstream position does the melting curve reveal two cooperative transitions, whereas freezing the all-T loop in the upstream or midstream position results in a single very cooperative melting transition. The latter is as expected for the all-T loop (pseudo)symmetrical construct containing a centrally located bulge loop, which also represents a control for melting of the constructs with off-center loops. Clearly, the position of the loop relative to the nonrepetitive duplex arms is important, an observation that becomes understandable when one considers that on the basis of nearest-neighbor free energy predictions, the downstream 11-mer arm is less stable (ΔΔG ≈ 1.5 kcal/mol) than the 11-mer upstream arm in our bulge loop construct. The simplest interpretation is that the presence of the all-T loop decouples the melting of the two duplex arms. Melting of the less stable 11-mer downstream arm occurs at lower temperature than the upstream arm when a destabilizing all-T bulge loop is nearby. The same destabilizing all-T bulge loop located near the more stable 11-mer upstream arm does not alter the melting temperature relative to the downstream arm. This result suggests that when loop migration is possible (e.g., as in extended triplet repeat domains), the distribution of positional isomer(s) influences the melting properties of the proximal duplex domains. Conversely, the differential properties of the proximal duplex domains influence the distribution of looped domains when loop migration is possible, as it is in extended repeat domains. Potential contributions from any differential loop topologies also could influence the interdependence of such neighboring domains.

Migrating Loops: Probing the Loop Distribution Using Fluorescent Base Analogues

If the above results from the “frozen” unstructured all-T loops apply to repeat loops in multiple possible states, one might conclude that the repeat loop would be located primarily near the downstream arm of the bulge loop construct rather than being equally distributed among all available positions. However, such a restricted distribution of loops at equilibrium seems unlikely given the entropic advantage of occupying all of the available loop positions, absent any obvious energetic reason to counteract this entropy gain.

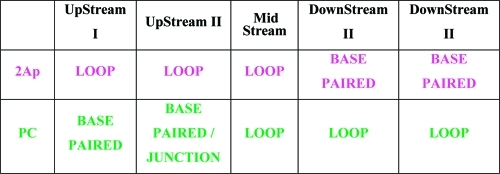
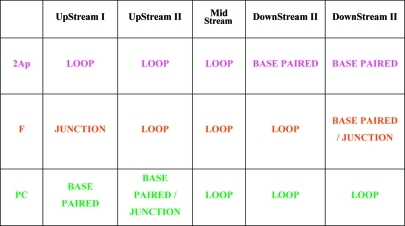
To assess the loop position/distribution, we followed the conceptual lead of the von Hippel group.⁶⁹⁻⁷¹ Specifically, we incorporated the fluorescent bases 2Ap and PC in repeats 3 and 6 of [CAG]₈, respectively, as cartooned in Scheme 2B for a “frozen”, centrally located loop and elaborated in Scheme 2C for the five rollamers produced within the [CAG]₈·[CTG]₄ construct. It should be noted that depending on the loop position, our siting of the two fluorophores in the [CAG]₈·[CTG]₄ complex ensures that when 2Ap is located in the duplex domain (and therefore is Watson–Crick base-paired), PC is located in the unpaired loop domain, and vice versa. Only when the loop is centrally located are both 2Ap and PC located in the loop, thereby having both reporter sites formally unpaired for this singular rollamer. Such partitioning of the fluorophores into different structural elements within different rollamers, as summarized in Table 1, provides an experimental means for detecting loop migration and monitoring the rollamerization process.

Table 1. Partitioning of Fluorophores within Different Structural Elements for the Different Structural Isomers/Rollamers in [CAG]₈·[CTG]₄.

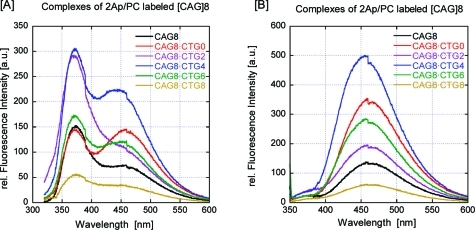
The two reporter fluorophores we chose are minimally perturbing mimics of their respective natural base analogues, adenine and cytosine, in terms of their base-pairing properties while being sensitive to DNA secondary structure.⁷²⁻⁷⁹ A comparison of CD spectra as a function of temperature, with and without these fluorescent bases, for all the [CAG]₈·[CTG]_n constructs (data not shown) revealed only minor differences in spectral and thermal properties, subtleties that can be attributed primarily to the spectral differences between fluorescent bases and their natural nonfluorescent analogues.⁸⁰⁻⁸² The CD data are consistent with the presence of the fluorescent bases not appreciably altering the conformational and thermal properties of the repeat bulge loop construct, for all constructs examined. A similar lack of impact of fluorescent base analogues on global repeat loop properties has been reported previously.^{45,47,49,50,70,83} In contrast, the fluorescence emission spectra of 2Ap and PC excited at their respective excitation maxima (Figure 3) show significant differences depending on whether the loop can exist in multiple loop arrangements (e.g., [CAG]₈·[CTG]₄) or in a fixed loop position (e.g., [CAG]₈·[CTG]₀) or when the repeat sequence is fully base-paired (e.g., [CAG]₈·[CTG]₈). Clearly, the fluorescence intensity is sensitive to the nature of the loop, reflecting changes in the environment surrounding the fluorophores due to loop size and positional distribution within the repeat sequence domain. The fluorescence intensity also may depend on potential energy transfer between the fluorophores. The steady-state fluorescence data confirmed that the loop was not located exclusively near either the upstream or downstream 11-mer arm, as the fluorescence intensities of 2Ap and PC were consistent with neither of these bases being fully base-paired. If one of these two positional isomers had been the exclusively occupied state (see Table 1), then either the 2Ap fluorescence or the PC fluorescence would have been strongly quenched, similar to what was observed for [CAG]₈·[CTG]₈, while the other base would have been highly fluorescent.

Figure 3.

Fluorescence excitation spectra at 25 °C (native) of the 2Ap- and PC-labeled constructs: (A) excitation at 305 nm, the 2Ap excitation maximum; (B) excitation at 340 nm, the PC excitation maximum. Shown are the steady-state emission spectra of constructs with an eight-CAG repeat loop in a fixed position (red), a six-CAG repeat loop in three possible loop positions (purple), a four-CAG repeat loop in five possible loop positions (blue), and a two-CAG repeat loop in seven possible loop positions (green). Also shown are the emission spectra of our construct when the repeat is fully base-paired (light-brown) and fully single-stranded (black). It should be noted that the PC fluorescence signal (460 nm peak) in (A) may be due in part to energy transfer from either 2Ap or the other bases, as PC excitation at this wavelength is at a minimum.

Temperature-Dependent Fluorescence Studies Reveal the Repeat Loop To Be Distributed throughout the Repetitive Domain and Duplex Domain Melting To Be Coupled with Loop Migration

The sensitivity of the 2Ap and PC fluorescence to the nature of the loop is reflected in the fluorescence melting curves for [CAG]₈·[CTG]₄ shown in Figure 4. The initial irreversible increase in the fluorescence of 2Ap centered around 45 °C, which was not seen in either the UV absorbance or DSC melting curves, is reflective of a local rather than a global event. This observation will be discussed in more detail later in this paper. For now, we concentrate our discussion on the two reversible fluorescence-monitored transitions that correspond to melting processes also seen in the DSC thermogram. In particular, the low-temperature transition detected in the DSC melting curves corresponds to a reversible cooperative fluorescence intensity decrease for 2Ap fluorescence and a reversible fluorescence intensity increase for PC. Although a number of possible photophysical effects may contribute to changes in fluorescence intensity,⁸⁴⁻⁹² it is customary to interpret a decrease in 2Ap fluorescence to signify a shift in the fluorophore from an unstacked, solvent-exposed (loop or denatured state) position to a solvent-shielded, base-paired/base-stacked position within a helical region, while an increase in fluorescence is interpreted as a signal of the reverse event.⁹³⁻⁹⁷ Assuming that this reasoning also applies to the PC fluorophore,^81,98,99 we conclude that the initial transition detected in the DSC curves reflects a structural rearrangement in which the 2Ap base (or the fraction of its population undergoing the transition) is transferred from a non-base-paired/loop state to a base-paired state while simultaneously the PC base (or the fraction of its population undergoing the transition) is transferred from a base-paired state to a denatured/coil state. Inspection of Scheme 2C reveals that such a rearrangement transition is possible when a fraction of the loop population is initially located near the upstream 11-mer domain, while the downstream arm starts melting. Migration of the loop from its upstream position and merging with the now non-base-paired downstream domain would result in the 2Ap fluorophore being transferred from the looped state to a base-paired domain with a simultaneous transition of PC from a base-paired domain to a nonbase-paired/denatured state, events in agreement with our experimental results. Such a process also reconciles the two melting transitions observed for the repeat loop in multiple arrangements with our observations on the “frozen” all-T loops described above. The subsequent high-temperature fluorescence intensity increase detected for 2Ap that partially overlaps the increase detected for PC reflects dissociation of the residual duplex domain. This interpretation explains the inability to fit the DSC curves using a two-state model, as a concerted melting/loop migration event for the first transition is not a two-state process.

Figure 4.

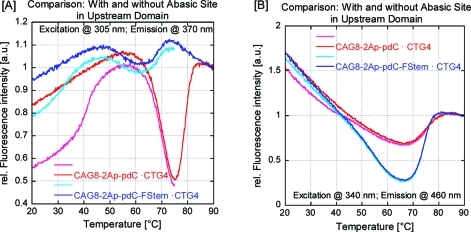
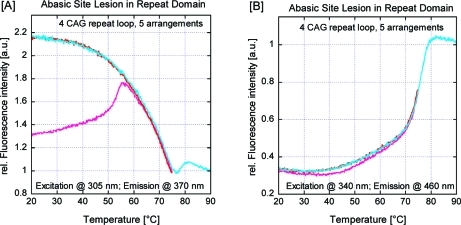
Fluorescence-detected thermal denaturation of the 2Ap/PC-labeled [CAG]₈·[CTG]₄ construct (four-repeat loop, five arrangements), with (blue) and without (red) a THF abasic site lesion in the upstream duplex arm, monitored at (A) the 2Ap excitation/emission maximum and (B) the PC excitation/emission maximum. To facilitate comparisons, these curves have been scaled/normalized such that the fluorescence of the fully denatured complexes at 90 °C is equal to 1. The initial irreversible transition (light-red/light-blue) that is seen in the first heating but absent during subsequent heating/cooling steps (dark-red/dark-blue) should be noted. Also noteworthy is the 2Ap fluorescence intensity decrease at 65–75 °C that coincides with an increase in PC fluorescence intensity for the construct lacking the abasic site lesion, which is reversed in the construct containing the abasic site lesion in the upstream arm.

Coupling of Loop Migration and Duplex Domain Melting: Preferential Loop Migration toward the Initial Melting Domain

As a further test of the proposed model, we thermodynamically destabilized the upstream duplex arm by replacing the guanidine nucleotide six base pairs from the 5′ end by a destabilizing THF abasic site. This site change results in an inversion of the temperature-dependent fluorescence behavior of the 2Ap and PC reporter sites. Specifically, in this case we observed at low temperature a gradual increase in 2Ap fluorescence coupled with a decrease in PC fluorescence due to denaturing of the upstream arm and loop migration into the denatured domain, while at higher temperature a cooperative transition for the PC fluorescence revealed the dissociation of the remaining downstream arm. These results do not indicate that the loop is exclusively located near the upstream domain but rather show that within a significant fraction of constructs, the loop is located such that 2Ap remains outside a base-paired domain prior to the first thermal transition, which requires the loop to be located near the upstream domain.

In the aggregate, these results support the hypothesis that the repeat loop indeed shows a distribution of loop states that one would predict on the basis of entropic considerations. In addition, these results also suggest that disruption of a (relatively) distant domain can cause loop migration toward the denatured domain, a feature that may be important for DNA repair processes in nearby repeat sequences. Such directed loop migration and merging of the loop with an adjacent denatured domain also may be of importance for understanding complex melting profiles of heterogeneous DNAs such as plasmids and viral DNAs and others containing repetitive DNA sequences.^62,100−102 Although the potential for migration of loops to merge with denatured domains has been discussed as a theoretical possibility,^103−105 to the best of our knowledge, this study provides the first direct experimental evidence for it in such Ω-like DNA constructs.

Impact of an Abasic Site within the Repeat Domain on the Loop Distribution: Preference of the “Universal Hinge” Abasic Site for the Loop/Duplex Junction and the Loop Center

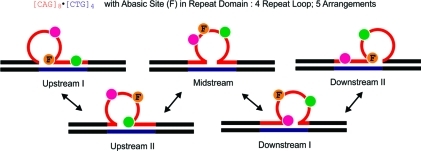
We previously proposed that the differential thermodynamic impact of lesions in repeat bulge loops relative to lesions in Watson–Crick duplex domains favors partitioning of the damage site into the bulge loop state,^48,55,56 thereby minimizing the destabilizing impact of the lesion on the overall domain. Recent work by Delaney and co-workers is consistent with this model.¹⁰⁶ To build on and further test this proposition, we performed a “site-directed mutation” experiment by substituting an abasic site for one of the G residues within a CAG repeat located between the 2Ap and PC fluorophores. As outlined in Scheme 4 and summarized in Table 2, such a placement of the abasic lesion between the fluorophores results in a characteristic pattern of distribution of 2Ap and PC in the different loop positional isomers, thereby allowing identification of which rollamer is preferentially populated.

Scheme 4. Schematic of the Different Positional Loop Isomers for [CAG]₈·[CTG]₄ (Five Equivalent Loop Arrangements) Indicating the Locations of the Abasic Site Lesion between the Fluorescent Labels and the Partitioning of These Modified Bases in Different Structural Domains within Different Loop Isomers.

The fluorescence data indicate that the most highly populated isomer is the isomer labeled “Upstream I”, which partitions the 2Ap fluorophore in the loop domain, the abasic site at the downstream loop/duplex junction, and the PC fluorophore in the downstream base-paired domain.

Table 2. Partitioning of the Fluorophores and Abasic Site Lesion with the Repeat Domain within Different Structural Elements for the Different Structural Isomers/Rollamers [CAG]₈·[CTG]₄.

On the basis of characteristic changes in the thermal denaturation patterns and 2Ap and PC fluorescence changes for our selectively labeled migrating bulge loop construct (Figure 5), we propose that the presence of an abasic lesion in place of dG within the repeat domain results in a redistribution of loop arrangements. Specifically, as outlined in Table 2, maximal 2Ap fluorescence coupled with maximal PC quenching suggests that in a significant fraction of the populations of our construct, the loop is located in the Upstream I position. Consequently the data indicate that the abasic site is preferentially accommodated in the junction between the duplex and bulge loop domains, forming what we characterize as a “universal hinge” between separate DNA structural elements. Such favored partitioning of abasic sites to junction domains may be driven by the ability of this universal hinge to relax unfavorable interactions between bases in the densely packed junction region. This interpretation is consistent with the impact of additional unpaired bases and abasic sites in three-way junctions.¹⁰⁷

Figure 5.

Fluorescence-detected thermal denaturation of the 2Ap/PC-labeled [CAG]₈·[CTG]₄ construct (four-repeat loop, five arrangements) containing a THF abasic site lesion between the fluorophores within the triplet repeat sequence, with melting monitored at (A) the 2Ap excitation/emission maximum (305 nm/370 nm) and (B) the PC excitation/emission maximum (340 nm/460 nm). To facilitate comparisons, these curves have been scaled/normalized such that the fluorescence of the fully denatured complexes at 90 °C is equal to 1. The same initial irreversible transition (light-red curve) observed in the first heating but absent during subsequent heating/cooling steps (light-blue and dark-red) as seen in Figure 4 is present. Also noteworthy is the gradual decrease in 2Ap fluorescence intensity at temperatures near or above the initial irreversible transition detected in the first heating, which is coupled with a gradual increase in PC fluorescence. These gradual fluorescence changes occur at temperatures much lower than the temperatures where denaturation is detected by temperature-dependent UV absorption measurements, suggestive of increased loop migration (rollamerization) at these temperatures.

Activation Energy for Loop Migration

The initial irreversible cooperative transition observed in Figures 3 and 4 in the fluorescence melting curve for [CAG]₈·[CTG]₄ during the first heating was also seen in CD spectral contributions assigned to the fluorophores (>300 nm) but not in either the UV absorbance-monitored or DSC melting curves. Taken together, these observations are consistent with local rearrangements in the vicinity of the fluorophores that are isoenthalpic and therefore not detected by DSC. The most plausible interpretation is that the process involves rearrangements and/or redistribution of the repeat loop within the repetitive sequence domain of our construct. Single-stranded DNA with highly repetitive sequences, such as those used here, are known to fold extensively at room temperature. Consequently, it is reasonable to propose that the initial formation of the complex between the [CAG]_m and [CTG]_n strands gives rise to a biased (kinetically trapped) distribution of loop states that is different from an equilibrium distribution. The presence of an abasic site lesion would further impact this biased/kinetically trapped distribution of loop states. Consistent with this interpretation, we previously demonstrated that repeat bulge loops can become trapped in high-energy metastable states that persist until sufficient thermal energy is provided to allow rearrangement to the equilibrium distribution (ref (35) and unpublished results). Consequently, as part of the loop migration rollamer model proposed here, we observe a temperature-induced rearrangement of kinetically trapped states to an equilibrium loop distribution of states. Considering that loop migration would require transient disruption and formation of base pairs in the stem and base interactions in the loop domain, processes that require energy input, such an interpretation is reasonable. From these collective observations, we conclude that the loops do not freely migrate between different states/arrangements at low temperatures but that loop migration is feasible in response to an external energy source, in this case, elevation of temperature. The denaturation of a neighboring domain acting as a sink (as discussed above) could induce loop migration, as perhaps could the DNA processing machinery through mechanical action on neighboring domains. It should be noted that the rearrangement reaction results in an overall increase in 2Ap fluorescence intensity; in other words, it proceeds from a state where 2Ap is quenched to one where it is far less quenched, likely the state where, in a significant fraction of the population, the 2Ap base is partitioned in the loop domain.

Reversible Annealing Leads to Disruption of a Preformed Base-Paired Domain upon Repeat Loop Formation

The fluorescent denaturation curves and the DSC melting curves are completely reversible upon cooling, with the exception of the irreversible low-temperature loop redistribution process discussed above. If a two-step denaturation process is assumed, then the fluorescence reannealing data suggest this process to be exactly reversed during cooling. Initial formation of the stable upstream arm at high temperature includes base pairing of the repeats surrounding the 2Ap probe, as shown by the 2Ap fluorescence intensity decrease. This event is followed by loop formation at lower temperature. However, loop formation results in the disruption of at least some fraction of the base-paired domain initially formed, as indicated by the increase in 2Ap fluorescence. In other words, the secondary structure formed at high temperature is disrupted again by repeat loop formation at lower temperature. This observation is of considerable interest, as formation of the repeat loop in principle could occur with the repeat loop located exclusively near the downstream domain and without the need to disrupt the base-paired repeat region near the upstream 2Ap-containing domain. However, we have found experimentally that bulge loop formation is coupled with disruption of at least some of the upstream base-paired domain. Disruption of the base-paired domain coupled with loop migration is an overall enthalpy-neutral event, as an equal number of base pairs are broken and formed. Consequently, the driving force must be the entropy gained by distributing the loop in multiple arrangements within the repeat domain (a Boltzman entropy) as opposed to maintaining the loop in a single position. The important observation here is that higher-order DNA interactions are able to disrupt preexisting DNA secondary structure interactions, even when there is no net enthalpy gain associated with the process. (The enthalpy and free energy gains due to base-pair interactions in the 11-mer downstream arm remain the same whether the loop is in a “frozen” position or in multiple positions.) Tertiary-structure-induced disruption of secondary structure is a common feature in protein folding.^108−110 It has also been postulated for RNA but is considered to be of minor importance for RNA folding processes.^111−113 To the best of our knowledge, such disruption of base-pairing interactions induced by higher-order structure has heretofore not been demonstrated for DNA in the absence of concomitant ligand binding. Such coupled structural rearrangement processes may have significant biological roles/consequences.

Impact on DNA Processing Machinery

DNA expansion occurs as a consequence of misdirected DNA replication, recombination, and repair processes. The observation of dynamic repeat bulge loops that are able to move within the larger repeat sequence domains immediately suggests the potential for loop migration during de novo DNA synthesis, during replication/recombination, or during repair as a potential reason for DNA expansion. Such migration could be facilitated by the mechanical forces exerted by the various DNA processing machineries, with their modes of action providing some of the activation energy for loop migration. Our observations further suggest that even the action of the DNA processing machinery in domains adjacent to the repeat sequence can facilitate loop migration/merging with the domain being processed, thereby potentially stimulating DNA expansion. The potential for repeat bulge loops to be found at multiple locations within the repeat domain and for loops to migrate between such locations likely enhances the potential for entrapment of critical components of the replication, recombination, or repair machinery in nonfunctional states. McMurray and co-workers have shown that such trapping of a critical component of the mismatch repair machinery in nonfunctional states is important and suggested that dynamic processes of repeat bulge loops and bulge loop junctions may help regulate repair success or failure in mismatch repair.^36,114,115 The Boltzman entropy gain for dynamic ensembles may be one factor contributing to the puzzling size dependence of triplet repeat expansion characteristic of triplet repeat expansion diseases.

Our results also suggest the intriguing possibility that oxidative damage and its repair by the BER pathway can result in multiple conformational adjustments within repeat domains that directly impact the repair process. Specifically, the results reported by Delaney and co-workers suggest that repeat DNA can minimize the thermodynamic impact of oxidative damage by partitioning the damaged base into the repeat loop domain.¹⁰⁶ Subsequent cleavage of the damaged base by OGG1 and related DNA glycosylases of the BER pathway results in an abasic site intermediate that we have shown here to be partitioned preferentially at the junction between repeat loop and an adjacent duplex domains. The potential for such conformational rearrangements to position damage sites or repair intermediates at the loop apex and/or loop junction may hamper the effectiveness of the BER machinery, which is optimized to process lesions within the context of Watson–Crick duplex DNA. In support of this hypothesis, Delaney and co-workers showed that 8-oxoG lesions found in mimics of repeat bulge loops are processed less efficiently by OGG1 than are lesions in duplex DNA.^44,116 We propose that such conformational rearrangements to accommodate lesions and repair intermediates, several of which we have probed here, contribute to the processes that lead to the erroneous expansions of DNA repeat sequences, the genotypical signature of a broad spectrum of developmental diseases.

Conclusion

We have shown that repeat bulge loops are able to redistribute within larger repetitive sequence domains. We have presented evidence that loop migration between different isoenergetic loop positions is feasible, with energy input being required to convert from a kinetically biased loop distribution of states to an equilibrium-directed distribution. Such dynamic ensembles of rollamers can be considered as creating DNA waves within the energy landscape that map to special DNA sequence domains. The resulting soliton-like propagated perturbation may allow for communication between distal sites, dynamic alteration of pre-existing structural elements, accommodation of damaged lesion sites, and selective trapping (conformational selection) of processing enzymes. Collectively, the modulatory influences of such DNA waves could result in both regulation and dysregulation of crucial biological pathways.

In summary, we have shown repeat bulge loop structures to be dynamic ensembles of loop positional isomers. We have demonstrated that the presence of lesions/repair intermediates biases the distribution of loop arrangements within a larger repeat domain to minimize the energy cost associated with accommodating the modification. We have found that higher-order DNA structure formation can disrupt preformed secondary structure elements. We have also speculated about how these collective characteristics of repeat loop dynamic ensembles may influence pathways leading to DNA expansion.

Supporting Information Available

Scheme depicting different loop arrangements. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States