Ultra-Small-Angle X-ray Scattering – X-ray Photon Correlation Spectroscopy Studies of Incipient Structural Changes in Amorphous Calcium Phosphate Based Dental Composites

Abstract

The local structural changes in amorphous calcium phosphate (ACP) based dental composites were studied under isothermal conditions using both static, bulk measurement techniques and a recently developed methodology based on combined ultra-small angle X-ray scattering – X-ray photon correlation spectroscopy (USAXS-XPCS), which permits a dynamic approach. While results from conventional bulk measurements do not show clear signs of structural change, USAXS-XPCS results reveal unambiguous evidence for local structural variations on a similar time scale to that of water loss in the ACP fillers. A thermal-expansion based simulation indicates that thermal behavior alone does not account for the observed dynamics. Together, these results suggest that changes in the water content of ACP affect the composite morphology due to changes in ACP structure that occur without an amorphous-to-crystalline conversion. It is also noted that biomedical materials research could benefit greatly from USAXS-XPCS, a dynamic approach.

Introduction

Amorphous calcium phosphate (ACP) has been recognized as a possible transient precursor in the biomineralization of hydroxyapatite (HAP), the main inorganic component of mineralized bone and tooth tissues ^1-5. Transient ACP is also found in newly formed enamel, the hardest and most mineralized human tissue that eventually transforms into apatitic crystals⁶. These discoveries have advanced our understanding of the mechanisms involved in the in vivo biomineralization process and provide clues for the basic principles needed by material scientists to facilitate fabrication of bone and dentin-like materials for tissue preservation and regeneration. One promising approach is to use ACP-based polymeric composites as preventive or restorative dental materials ^7-10. These composites have been shown to promote recovery of mineral-deficient tooth structure in in-vitro remineralization studies of caries-like lesions artificially produced in bovine and human enamel ^11,12. For this application, recovery occurs even when only a small fraction of the theoretically available mineral ions are released into the external aqueous solution.

Despite these advantages, ACP composites trail behind conventional glass-based dental composites in terms of mechanical strength.¹⁰ Many treatments, such as filler hybridization ^13,14 or milling ^15-17, surface treatment of the filler ⁹, and use of various methacrylic polymer matrices ^18-21, have been explored for optimizing the mechanical properties of the ACP-based dental composites for potential clinical applications. Notably, a comparison of wet and dry ACP composites showed that the biaxial flexure strength of the composites is strongly related to the uptake of water in these composites– more water, less strength and vice versa.¹⁰ This result directly suggests that the presence of water both in the ACP filler phase and the polymeric matrix phase may adversely affect the local microstructure of ACP composites and, consequently, their mechanical properties. It is also known that the exposure of ACP composites to aqueous milieus leads to plasticization of the organic polymer matrix and conversion of ACP to crystalline apatitic calcium phosphate.

ACP-based polymeric composites that are intended for dental applications have highly complex microstructures, where the interaction of different components can strongly affect the macroscopic behavior. To elucidate the critical role that water plays in these systems, we separated the problem into two parts. First, in this paper, we investigate the degree of water loss with time upon modest heating, and coordinate this with sensitive, dynamic probes of the sample microstructure. Later work will contrast these results with behaviors in a wet environment where water exchange can occur. This current study also examines these processes within real-world dental composites. More restricted studies of individual components such as pure ACP would likely fail to identify the most important phenomena occurring in composite formulations intended for real dental applications. Two dental composite formulations are explored; both of these are composed of ACP particles embedded in a photo-activated (2, 2-bis[(p-2′-hydroxy-3′-methacryloxypropoxy)phenyl]propane (Bis-GMA) and triethyleneglycol dimethacrylate (TEGDMA) resin. In the first formulation, the ACP particles are uncoated. In the second, the ACP particles are surface treated with 3-methacryloxypropyl trimethoxysilane (MPTMS) to achieve surface silanization. This surface treatment is expected to significantly affect both the mechanical behavior of the composite and the transportation of water through the system.

The main hurdle in elucidating how water affects the detailed arrangement of ACP composites lies in the difficulty of both static and dynamic characterization methods to provide sufficient information about local structure in amorphous materials. Bulk characterization techniques lack the required sensitivity, and often fail to capture the details that are associated with exact arrangements of local microstructure. That is to say, statistically averaged results, although meaningful in their own right, do not represent individual local structures and cannot be used to monitor local dynamic structural changes. Thus, a sensitive local probe is required.

To monitor local structural changes and dynamics in the scale range appropriate to ACP polymer dental composites, some of the present authors have developed a combined ultra-small-angle X-ray scattering – X-ray photon correlation spectroscopy (USAXS-XPCS) technique ^22,23. USAXS-XPCS is similar to conventional X-ray photon correlation spectroscopy (XPCS) ^24-26 in the sense that both techniques take advantage of the coherent interference of short-wavelength (≈ 1 Å) X-ray radiation to provide high spatial sensitivity These methods rely on the fact that a particular arrangement of atoms within the sampling volume produces a characteristic “speckle” pattern when a coherent beam of X-rays is scattered by the sample. If the arrangement of atoms changes, the speckle pattern changes, and by studying these changes as a function of time, information on the structural dynamics at various length scales can be obtained. Both methods provide the dynamic time scale of the underlying physical processes. Conventional XPCS has enjoyed great success in studying equilibrium dynamics on the nanometer scale, especially that of various complex fluids. USAXS-XPCS has been developed to fill a gap in the length-scale range between those of XPCS (nanometers) and dynamic light scattering (micrometers).²² Compared with conventional XPCS, USAXS-XPCS is more suitable for this study since it can probe systems with both larger length and longer time scales, especially in situations governed by non-equilibrium dynamics.

In the next section, we briefly introduce the materials studied, and the techniques used to characterize them. Then, we discuss the USAXS-XPCS data analysis method and introduce a simplified simulation for analyzing the role of thermal expansion in the microstructural changes observed. We then proceed to present our detailed results from both bulk characterization techniques and from USAXS-XPCS measurements, followed by concluding remarks.

Materials and Methods

Materials

Zirconium hybridized ACP fillers were synthesized following the protocol of Eanes et al ²⁷. Pyrophosphate-stabilized ACP was precipitated at 23 °C during rapid mixing of equal volumes of an 800 mmol/L Ca(NO₃)₂ solution and a solution of 536 mmol/L Na₂HPO₄ incorporating 2 % mass fraction Na₄P₂O₇ and an appropriate volume of a 250 mmol/L ZrOCl₂ solution (mole fraction of 10 % ZrOCl₂ based on the Ca reactant). The reaction pH was set between 10.5 and 11.0. Mixing occurred in a closed system under CO₂-free N₂ to minimize CO₂ adsorption by the precipitate. This ACP is denoted as unsilanized ACP (uns-ACP) ²⁸. The uns-ACP powders were then surface-treated with MPTMS at 10 % mass fraction relative to ACP to achieve surface silanization ²⁹. We denote these surface-coated ACP particles as silanized ACP (sil-ACP). Commercially available barium boron aluminum silicate glass fillers were obtained from Caulk/Dentsply^*, Milford, DE, USA; lot # 07033). A similar procedure was followed to surface-treat the glass fillers with MPTMS. We denote the untreated and treated glass fillers as uns-glass and sil-glass, respectively.

The polymer matrix was formulated from commercially available dental monomers and photo-initiators used for visible light polymerization. Bis-GMA and TEGDMA were used as the base and diluent monomer, respectively, in a 50:50 mass ratio. Bis-GMA/TEGDMA resin was photo-activated by the inclusion of camphorquinone (mass fraction 0.2 %) and ethyl-4,4-N,N-dimethylaminobenzoate (mass fraction 0.8 %). The names, acronyms, sources of the monomers, components of the photo-initiator system and fillers are listed in Table 1.

Table 1.

Chemical names, acronyms, and sources of the composite components.

Acronym	Name	Source
Bis-GMA	2,2-bis[(p-2′-hydroxy-3′- methacryloxypropoxy)phenyl]-propane	Esstech, Essington, PA, USA
TEGDMA	triethyleneglycol dimethacrylate	Esstech, Essington, PA, USA
CQ	camphorquinone	Sigma-Aldrich, St. Louis, Mo, USA
4EDMAB	ethyl-4,4-N,N-dimethylaminobenzoate	Sigma-Aldrich, St. Louis, Mo, USA
ACP	amorphous calcium phosphate	Paffenbarger Research Center
HAP	hydroxyapatite	Paffenbarger Research Center
MPTMS	3-methacryloxypropyl trimethoxysilane	Gelest, Morrisville, PA, USA
uns-glass	barium boron aluminum silicate glass	Caulk/Dentsply, Milford, DE, USA

Composite pastes were formulated by hand-mixing photo-activated Bis-GMA/TEGDMA resin (60 % mass fraction) and the chosen filler (40 % mass fraction). The pastes were mixed until a uniform consistency was achieved, with no remaining visible filler particulates, and then kept under moderate vacuum (2.7 kPa) overnight to remove air trapped during mixing. The pastes were molded to form disks (≈ 10 mm diameter, ≈ 1 mm in thickness) by filling the circular openings of flat Teflon molds. The filled molds were covered with mylar films and glass slides, and then clamped tightly with spring clips. The composite disks were cured by means of a 120 s photo-polymerization procedure described elsewhere (Triad 2000, Dentsply International, York, PA, USA; ⁸). A minimum of three disks were made for each type of composite so that measurements performed on samples from the same batch could be compared. The glass-based polymer composites serve as a baseline for ACP-based composites. All the composites were stored in dry air for at least 24 h.

Characterization Methods

X-ray diffraction

X-ray diffraction (XRD) measurements were made using a Rigaku DMAX 2000 X-ray diffractometer (Rigaku USA Inc., Danvers, MA, USA) operating at 40 kV and 40 mA. XRD patterns of the ACP fillers placed in Al holders were recorded in a scattering angle, 2θ, range of 4° to 60° with a step size of 0.010^° and a scanning speed of 1.000°/min. XRD patterns were obtained before and after heating at 125 °C for 3 h.

Fourier transform infrared spectroscopy

Fourier transform infrared spectroscopy (FTIR) spectra of the sample disks were recorded in the wave-number range of 4000 cm⁻¹ to 400 cm⁻¹ using a Nicolet Magna-IR FTIR 550 spectrophotometer (Nicolet Instrument Corporation, Madison, WI, USA) with a resolution of 2 cm⁻¹. Spectra were acquired before and after heating (as specified for XRD).

Scanning electron microscopy

In order to evaluate the morphological/topological features of the disks, each specimen was sputter coated with gold under an argon atmosphere at room temperature. Sputtering took place at 65 μbar (50 mtorr) pressure and 45 mA current for a duration of 90 s, giving a gold coating of ≈ 300 Å. The specimens were then observed via scanning electron microscopy (SEM) using a JEOL 35C instrument (JEOL Inc., Peabody, MA, USA) at 15 kV and an 11 mm working distance.

Thermo-gravimetric analysis

Isothermal thermo-gravimetric analysis (TGA) was carried out using a Thermogravimetric Analyzer (Q500; TA Instruments, New Castle, DE, USA). The composite disks were cut into small pieces and about 10 mg of material was placed in a platinum pan under a flowing nitrogen atmosphere (40 mL/min). The temperature was ramped to 125 °C at a rate of 25 °C/min. Once the target temperature was reached, it was maintained for > 14 h while the sample mass was monitored continuously. In addition, thermal decomposition profiles of powdered uns- and sil-ACP as well as uns-glass filler samples were determined (initial powdered sample mass: 5 mg to 10 mg). Powders were heated at a rate of 20 °/min from 30 °C to 600 °C in a flowing nitrogen atmosphere (40 mL/min).

Ultra-small angle X-ray scattering (USAXS) measurements

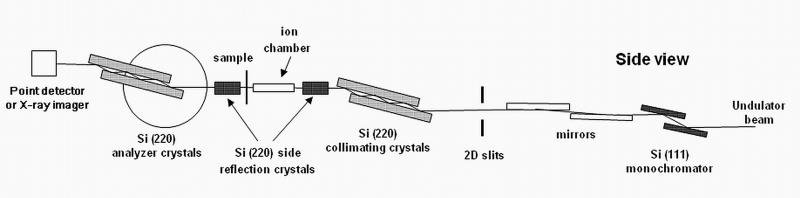
USAXS studies were conducted using the USAXS instrument at sector 32-ID (now at sector 15-ID) at the Advanced Photon Source (APS), Argonne National Laboratory, IL. ³⁰ This instrument (schematic shown in Fig. 1) employs Bonse-Hart-type double-crystal optics to extend the scattering vector q range of small-angle X-ray scattering (SAXS) down to 0.0001 Å⁻¹ (where q = (4π/λ)sinθ, λ is the X-ray wavelength, and θ is half the scattering angle). This q range is normally inaccessible to pinhole SAXS cameras. Collimated monochromatic X-rays were used in a standard transmission geometry to measure the scattering intensity as a function of q. The instrument was operated in 2D collimated mode with beam-defining slits set at 0.5 mm × 0.5 mm. The X-ray energy was 10.5 keV, corresponding to a wavelength of 1.18 Å. USAXS measurements were performed in the q range from 10⁻⁴ Å⁻¹ to 10⁻¹ Å⁻¹. The q resolution was 1.5 × 10⁻⁴ Å⁻¹ and the incident photon flux on the sample (in this instrument configuration) was on the order of 1 × 10¹² photons s⁻¹. Data were collected at 150 points, logarithmically distributed throughout the q range, and the data collection time for each data point was 1 s. The data were corrected for empty beam and detector backgrounds, and were normalized to the incident beam intensity to give the absolute scattering intensity or differential scattering cross-section, I(q) versus q.³⁰ The 2D-collimated USAXS data reduction and analysis were performed using the standard small-angle X-ray scattering data analysis packages, Indra and Irena.³¹

Figure 1.

Schematic of the USAXS and USAXS-XPCS instrument.

The sample disks were loaded into a custom-made sample cell with polyamide entrance and exit windows and a 1 mm X-ray scattering path. The temperature of the sample cell was controlled with a Linkam TH600 thermal stage (Linkam Scientific Instruments Ltd., Tadworth, UK) assisted with liquid nitrogen circulation for rapid heating and cooling. The heating/cooling rate was set at 50 °C/min. Several USAXS measurements were made at room temperature, target (elevated) temperature and room temperature (after cooling) for each sample.

USAXS-XPCS measurements

USAXS-XPCS measurements were also conducted with the USAXS instrument at the APS. A pair of 15 μm × 15 μm coherence-defining slits was placed in front of the collimating crystals as a secondary coherent source. The APS storage ring was used in both a conventional operating mode and in a special reduced horizontal beam size operation mode that provides greater coherence. We found that the operating modes of the storage ring weakly affect the quality of the beam coherence, but not the observed sample dynamics. The dynamics of the composite samples were studied in a scan mode 22, due to their non-equilibrium nature. A detailed procedure was established, as described below, to offer the best time resolution while maintaining the optimal alignment of the instrument.

The samples were loaded into the sample cell described above. In each case, once the sample temperature had reached the set-point (105 °C, 115 °C or 125 °C), a full, 100-point USAXS-XPCS scan was started, which covered a q range from –1.3 × 10⁻⁴ Å⁻¹ to +1 × 10⁻³ Å⁻¹, with the 15 μm × 15 μm partially coherent incident beam. The data-acquisition time for each data point was 1 s. We denote this as a “long” scan, which took ≈ 5 min to complete. Because long scans included the rocking curve section of the scattering profile, they provided an accurate determination of the forward scattering (q = 0) direction. Additionally, the long scans were used to determine the amount of sample attenuation of the X-ray beam, which served as a sensitive measure of any rare, abrupt change in the beamline configuration.

Five “short” scans over the q range: 1 × 10⁻⁴ Å⁻¹ to 1 × 10⁻³ Å⁻¹ were taken after each long scan. Each short scan contained 50 data points and took ≈ 2 min to complete (including the time for the USAXS stages to return to their starting positions). After one long scan and five short scans, the optics were re-tuned to verify that the instrument was still in optimal alignment before starting another set of long and short scans. The total measurement time was based on the amount of time required for the material system to reach equilibrium, i.e., until the scanning profiles (speckle patterns) no longer changed significantly, scan to scan. Depending upon the temperature, the total measurement time was as long as 6 h before an equilibrium state was achieved.

Analysis Methods

3.1 USAXS –XPCS analysis method

This section describes the detailed analysis of our USAXS-XPCS data, and offers a simulation that addresses the effects of thermal expansion. As previously described, USAXS-XPCS scanning over a finite q range has a limited time resolution that precludes simultaneous acquisition of coherent scattering intensities at different q values. Furthermore, upon heating or cooling, the ACP- or SiO₂-based polymer composites experience changes in the local arrangement of reinforcement particles due to creep in the surrounding polymer matrix and thermal mismatch between the particles and matrix. The nature of these dynamics is inherently non-equilibrium. These two factors make standard intensity autocorrelation analysis of XPCS data unsuitable. To overcome this challenge and to monitor the rate of change in these polymer composites, we developed an analysis method based on the simplest scalar, statistical measure of change quantifiable using a correlation coefficient. Although the data from each speckle pattern were not collected simultaneously, the data acquisition time resolution (≈ 1 min) was significantly shorter than the time scale of the probed dynamics (≈ 100 min). Under this condition, the speckle pattern, which is strictly related to the precise microscopic arrangement of the local structure, is approximately stable during each individual scan. Thus, a correlation coefficient can be defined that provides a satisfactory measure of the changes between different speckle patterns as a function of time.

One characteristic of USAXS-XPCS data is that the coherent scattering ranges over two decades in intensity. If each data point is given equal weight in a statistical analysis, the weighting of the low-q (high intensity) data overwhelms the results. A solution is to normalize the USAXS-XPCS data with corresponding USAXS data, which in the same q range cover a similar range of intensity. Also, the USAXS-XPCS intensity originates from a much smaller X-ray beam and sampling volume than does the USAXS intensity. As a result, the USAXS-XPCS scans are sensitive to small fluctuations in apparent sample transmission (attenuation). These can arise either from small incident beam changes not usually observable by USAXS, or from changes in the local sample attenuation due to fluctuations in the total speckle scattering, itself. In order to compensate for these effects, each of the USAXS-XPCS and USAXS datasets were first self-normalized using a function analogous to the small angle scattering invariant, a parameter commonly used in small angle scattering data analysis to derive the total volume fraction of the scattering features. With these considerations, we developed the following procedure:

1. Normalize the USAXS and USAXS-XPCS profiles with their respective small angle scattering invariants, A, defined by:

   $$A=\int I\left(q\right)q^{2}dq,$$ (1)

   where I(q) is the scattering intensity. Although, strictly, the above integral should be taken over the range from q = 0 to q = 4π/λ, only the USAXS-XPCS measurement range was used here. Given that the microstructure sampled by both USAXS and USAXS-XPCS should be statistically equivalent, use of the limited integration range is justified for this normalization.
2. At each q, calculate the ratio of the difference between the normalized USAXS-XPCS and USAXS intensities (numerator) and the normalized USAXS intensity (denominator):

   $${I^{\prime }}_{\mathit{XPCS}}\left(q\right)=\frac{{I^{\prime }}_{\mathit{XPCS}}\left(q\right)-{I^{\prime }}_{\mathit{USAXS}}\left(q\right)}{{I^{\prime }}_{\mathit{USAXS}}\left(q\right)},$$ (2)

   where I’_XPCS (q) and I’_USAXS (q) are the USAXS-XPCS and USAXS intensities each normalized by their own scattering invariant, A, defined by Eqn. 1. This method of normalization with I’_USAXS (q) gives approximately equal weight to intensity values that range over 2 decades across the measured q range.
3. Define the correlation coefficient ϕ(i, j), a statistical parameter that describes the degree of resemblance between two datasets, following

   $$\varphi (i,j)=\frac{C(i,j)}{\sqrt{C(i,i)C(j,j)}}.$$ (3)

   where i, j represent the i^th and j^th dataset, C(i,j) is the covariance of variables i, and j, and follows the standard statistical definition,

   $$C(i,j)=\langle (i-\langle i\rangle )\times (j-\langle j\rangle )\rangle ,$$ (4)

   where ⟨…⟩ represents the statistical mean.

4. Calculate the correlation coefficient between every pair of normalized USAXS-XPCS datasets, I"_XPCS (q), and draw conclusions from the evolution of the correlation coefficients. In the present case, we take advantage of the correlation coefficient to monitor the slow dynamics experienced by the composites by using a two-dimensional color map representation, or correlation coefficient map, discussed later in Section 4. We would like to point out that similar to DLS and XPCS, USAXS-XPCS is capable of revealing the dynamic time scale of the underlying physical process in the appropriate time and length scales. The correlation coefficient map developed for this purpose.

3.2 Thermal expansion simulation

To examine the effects of thermal expansion/contraction ^32,33 on the correlation coefficient map, we performed a first-principle simulation based on the coherent scattering of the composite samples. This wave-optics approach is similar to the phase propagation method commonly adopted in simulations of coherent X-ray imaging and scattering ^34,35.

The phase propagation contrast is introduced by the coherent interference of spherical waves from the imaging objects after being illuminated by an incident wave. In the far field at small scattering angles, the coherent scattering intensity in the detector is related to the complex amplitude of the wave at the exit interface of the sample. To calculate the transmitted wave, we define the complex refractive index in the X-ray regime as

$$n=1-\delta +i\beta ,$$ (5)

where δ is the refraction decrement and β is the imaginary attenuation decrement.

For a thin object illuminated by a plane wave propagating along the z-axis, the incident wave can be written as E_oe^−ikz, where k = 2π/λ , z is the sample to detector distance, and E₀ is the amplitude of the incident coherent X-ray wave. The transmitted complex field immediately after the object can be written as

$$E(x_0,y_0)=E_0{e}^{-ikz}\exp \left[i\varphi (x_0,y_0)-\mu (x_0,y_0)\right],$$ (6)

where

$$\varphi (x_0,y_0)=\frac{2\pi }{\lambda }\int \delta (x_0,y_0,z)dz,$$ (7)

and

$$\mu (x_0,y_0)=\frac{2\pi }{\lambda }\int \beta (x_0,y_0,z)dz.$$ (8)

Here, x₀ and y₀ specify a set of spatial coordinates. The intensity at the detector (in reciprocal space), following the standard Huygens-Fresnel treatment ³⁵ can be written as

$$E(q_x,q_y)=A^2{\mid \underset{-\infty }{\overset{\infty }{\int }}E(x_0,y_0)\times \exp \left[-i\frac{2\pi }{\lambda z}(q_{x}x+q_{y}y)\right]dxdy\mid }^2,$$ (9)

where A is a multiplicative factor, and q_x and q_y are the spatial components of the reciprocal vector q. Eqn. (9) explicitly shows that the coherent scattering intensity at the detector is proportional to the Fourier transform of the transmitted wave at the exit interface of the sample, and this forms the basis of the simulation. The simulated intensity distribution at the detector shows a 2D speckle pattern. Consequently USAXS-XPCS data are readily obtained along the vertical scan direction. Combined with Eqns. (1) to (4), correlation coefficient analysis can be carried out on these simulated data to analyze the thermal expansion effects under the simulation conditions.

To simplify the simulation without losing generality, we assumed that the X-ray wave impinging on the sample is spatially and temporally fully coherent, with a X-ray energy of 10 keV. Furthermore, since we employ this simulation to examine the effects of thermal expansion/contraction, we assumed that all the filler particles are uniform silica spheres with a radius of 1 μm. The sample thickness was set at 1 mm, and the size of the coherence defining aperture at 15 μm × 15 μm. The total size of the two-dimensional, 1024 × 1024 simulation grid was set at 50 μm × 50 μm to match the resolution of the crystal optics used in the experiments. The total number of the spheres used for the simulation was set at 10000, which is equivalent to a volume fraction of ≈ 0.2 (corresponding mass fraction ≈ 0.4). The positions of the spheres are randomly generated, without taking into account any excluded volume effects. The matrix was assumed to be Bis-GMA, instead of Bis-GMA and TEGDMA as in the samples. The refraction and absorption increments of both the silica spheres and the matrix are listed in Table 2. The transmitted wave was calculated using Eqn. 6, and its corresponding intensity distribution in the detector was calculated using Eqn. 9. An aliasing filter was applied to ensure that the Fourier transform is aliasing-free³⁵. The results were smeared over a square aperture in reciprocal space to correct for the finite widths of the USAXS analyzing crystal rocking curves (in both the vertical and horizontal planes) in order to better match the experimental data.

Table 2.

Calculated Refractive indices for SiO₂ and BisGMA.

	refractive decrement δ	Absorption decrement β
SiO2	4.598 × 10−6	3.866 × 10−8
BisGMA	2.668 × 10−6	0.292 × 10−8

To simulate the effect of the thermal expansion, we assumed that during heating the Bis-GMA matrix expands linearly with a linear coefficient of thermal expansion at 76 × 10⁻⁶ / °C ³⁶. In this temperature range, the thermal expansion of silica is much smaller than that of the polymer, and is therefore neglected ³⁶. Viscoelastic creep was not considered in this simulation. For each state of the expansion, we calculate the corresponding USAXS-XPCS and USAXS data. These data are then used to calculate the previously defined correlation coefficient and correlation coefficient map.

Results and Discussions

XRD patterns of sil-ACP and uns-ACP fillers before and after heating at 125 °C for 3 h are shown in Fig. 2. The applied heating regimen had no apparent effect on the structure of either uns-ACP or sil-ACP. The XRD spectra show only diffuse peaks typical of the amorphous material while the diffraction peaks characteristic of hydroxyapatite crystals ¹³ (also shown in the inset) are not observed, thus providing no indication of ACP’s conversion to a crystalline form. This conversion can be either solution mediated ¹³ or thermally induced at highly elevated temperatures (> 500 °C) ^37,38.

Figure 2.

XRD measurements for sil-ACP and uns-ACP fillers before and after heating at 125 °C for 3 h. These curves are shifted vertically for clarity. The inset shows the XRD profile of hydroxylapatite crystals.

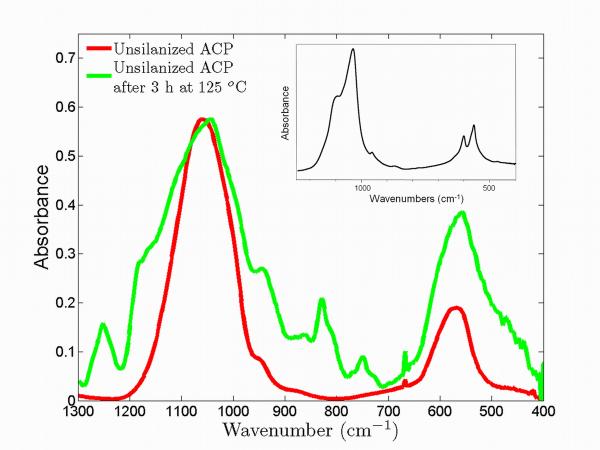
Fig. 3 compares the FTIR spectra in the wave-number range from 1300 cm⁻¹ down to 400 cm⁻¹ for the ground uns-ACP composites after heating at 125 °C for 3 h. In contrast to the peak splitting observed in crystalline hydroxyapatite¹³ (shown in the inset), the corresponding peaks in the composite samples show no evidence of splitting and no shift in peak position is observed. The location of these peaks is associated with the phosphate bending regime (630 cm⁻¹ to 500 cm⁻¹) and the minimal changes upon heating suggest that the bulk chemistry of the substituent group does not change. The shape of the peak, however, showed signs of broadening, which suggests a slight short-range structural arrangement change possibly originating from the early stages of ACP conversion to crystalline form at elevated temperatures. We also note that the other phosphate peak near 1050 cm⁻¹ cannot be interpreted with certainty, as there is interference with polymer- and possibly silane-related peaks. While XRD is definitively not sensitive enough to indicate very early stages of conversion; FTIR appears somewhat more sensitive to the structural variation related to prolonged heating. Similar results were found for sil-ACP samples.

Figure 3.

FTIR measurements for uns-ACP composite samples before and after heating at 125 °C for 3 h. The inset shows the FTIR spectrum of the crystalline hydroxylapatite.

Typical SEM micrographs are shown in Fig. 4. While uns-glass fillers appear well dispersed in the polymer matrix, the sil-ACP fillers form agglomerates with a wide size distribution. Particle size distribution analysis (not shown) suggests that the ACP agglomerate sizes range over several micrometers while the nominal size of the glass fillers is close to 1 μm. The agglomeration of ACP particles in ACP composites is the main reason why the mechanical strength of these composites does not reach its theoretical value¹⁷. Mechanical methods such as ball-milling have been shown to improve the biaxial flexural strength of ACP composites ^15,16, further indicating that the ACP particles are agglomerated. The primary ACP particle size is significantly smaller than the agglomerates, as is shown (below) by conventional USAXS measurements.

Figure 4.

SEM images of (a) sil-ACP composites and (b) uns-glass composites.

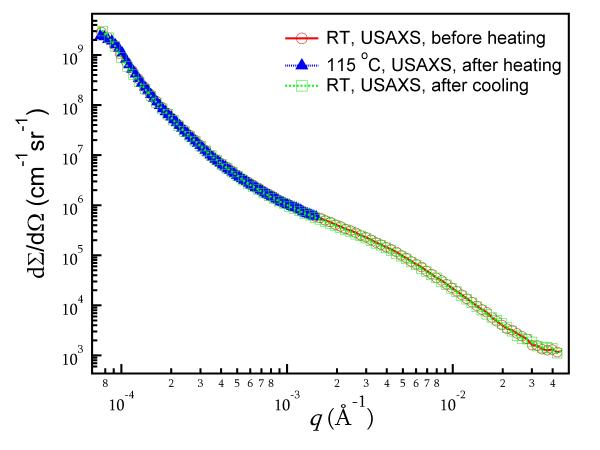
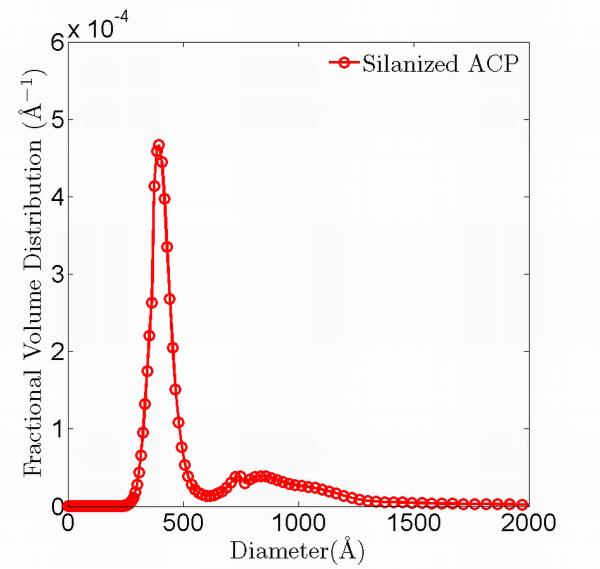
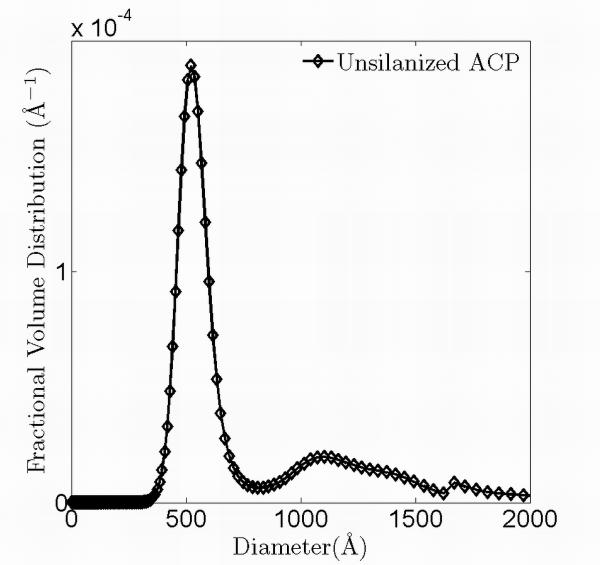
Fig. 5 shows typical USAXS data before heating, at 115 °C, and after cooling to room temperature. The time difference between the initial USAXS data measured before heating and the final USAXS data measured after cooling is ≈ 6 hours. The datasets overlap throughout the entire q range, demonstrating that the statistically representative microstructure sampled does not change. We applied a maximum entropy (MaxEnt) size distribution analysis to the USAXS data ³¹. The MaxEnt method does not make a priori assumptions about the type of the particle size distribution. However, it was assumed that the ACP particles are spherical in shape, as suggested in previous work ³⁹. The calculated scattering length (X-ray form-factor) densities of the fillers and the matrix are shown in Table 3, together with the scattering contrast factors used in the MaxEnt analysis. Fig. 6(a) and 6(b) show the resulting size distribution of the ACP fillers. Both types of ACP filler particles show a binary size distribution; the nominal size and volume fraction of each population is listed in Table 4. The slight difference in the size of the primary particles is attributed to the different sample batches used in these measurements. Similarly, the size distribution of the glass fillers was also analyzed (data not shown) and their nominal sizes are listed in Table 4 as well. A comparison of the results for sil-ACP with uns-ACP shows that these sizes are consistent with a wide range of in-vivo and in-vitro ACP studies^6,39-41. This suggests that ACP has an energetically preferred size range. However, these nominal sizes of ACP are much smaller than those found in the SEM measurements, as shown in Fig. 4, again indicating that strong agglomeration of the primary ACP particles occurs. The glass particles, on the other hand, show a single-peaked distribution with the USAXS data showing no signs of agglomeration, consistent with the SEM observations. A comparison of the USAXS data before and after heating shows no significant differences. This indicates that no transformation in the statistically representative microstructure occurs.

Figure 5.

A comparison of USAXS data for silanized ACP/Bis-GMA composite: at room temperature (RT) before heating, after heating at 115 °C, and after cooling to room temperature. Statistical uncertainties for the individual data points are smaller than the size of the symbols plotted.

Table 3.

Experimental Parameters for the fillers and the matrix and their X-ray scattering length densities. Scattering length densities are calculated with the scattering length contrast calculator of the Irena SAXS analysis package.³¹

	Formula	Density (g cm−3)	Molecular mass	Scattering length density ( 1014 m−2)	Contrast factor with 50BisGMA: 50TEGDMA (1028 m−4)
ACP	Ca3(PO4)2.3H2O*	2.04	364.22	17.40	42.38
BisGMA	C29H36O8	1.20	512.60	10.89	0
TEGDMA	C14H22O6	1.20	286.33	10.90	0
glass	Al0.055B0.23Ba0.22Si0.86O2.6	2.90	99.90	23.10	148.96

^*Approximate formula.^44,46

Figure 6.

Volume fraction size distribution of the sil-ACP (a) and uns-ACP (b) fillers obtained with MaxEnt analysis.

Table 4.

Fitting parameters from MaxEnt analysis. The uncertainties are shown in the parentheses.

Sample	Mean primary diameter (Å)	Primary volume fraction	Mean agglomerate diameter (Å)	Agglomerate volume Fraction	Total volume fraction	Total mass fraction
Sil- ACP	401(1)	0.28(1)	835(1)	0.15(1)	0.43(1)	0.56(1)
Uns- ACP	527(1)	0.17(1)	1157(1)	0.09(1)	0.26(1)	0.37(1)
Glass	3045(1)	0.44(1)			0.44(1)	0.69(1)

The inability of the bulk characterization methods such as XRD, FTIR, SEM, and USAXS to detect structural changes conclusively has two implications: heating of the ACP composites at the experimental temperatures does not induce structural change in the samples, or these bulk techniques are inadequate for detecting local changes. To distinguish between these two possibilities, USAXS-XPCS, a local structural probe which is sensitive to the exact arrangements of microstructural features within the sample was employed.

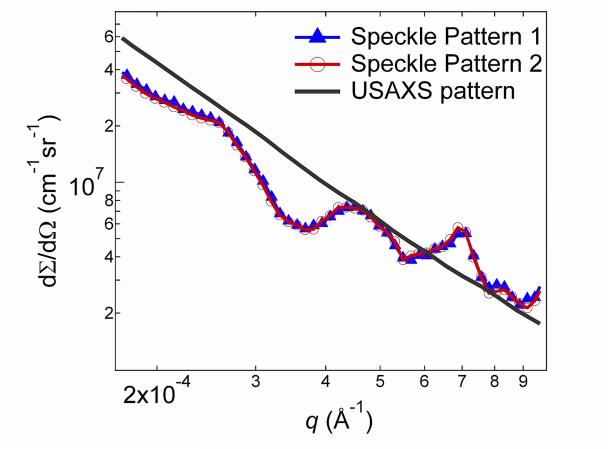
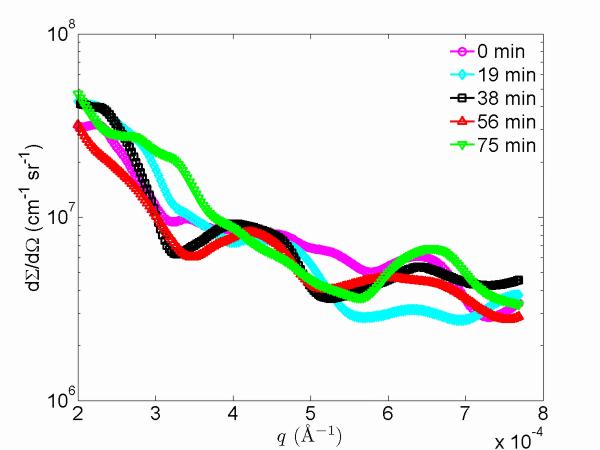
Fig. 7(a) shows typical USAXS-XPCS data. In a static condition, consecutive USAXS-XPCS scans exhibit identical speckle patterns, as illustrated in Fig. 7 (a), which shows two scans taken ≈ 10 min apart on a sil-ACP composite sample. Thus, without external perturbation to the sample, the USAXS-XPCS data reflect the static microstructure and the speckle pattern signal level is significantly above any background noise. This means that any observed change in the speckle pattern can be attributed to changes in the sample microstructure, which consequently allows monitoring of the non-equilibrium dynamics of the sample with USAXS-XPCS. It is also noticeable that the USAXS data are smooth over the entire q range, while USAXS-XPCS data show “peaks” that are related to coherent scattering from the local microstructure sampled. Any change in the local microstructure due to an external stimulus should be reflected in the speckle pattern. An example of this is presented in Fig. 7 (b), which shows successive USAXS-XPCS scans of an uns-ACP composite sample collected at 105 °C at 0 min, 19 min, 38 min, 56 min, and 75 min after the start of heating. The speckle patterns, originating from coherent X-ray interference associated with the change of local microstructure, no longer overlap. In contrast to the USAXS findings (Fig. 5), this result directly shows how USAXS-XPCS measurements are sensitive to local structural variations not observed using a bulk, static scattering technique such as USAXS where scattering intensities from different parts of the relatively large incident X-ray beam are summed incoherently.

Figure 7.

(a) A comparison of USAXS-XPCS speckle profiles and the associated USAXS data. While the USAXS data are smooth over the q range, USAXS-XPCS data show peaks and troughs that relate to the coherent scattering of the local microstructure. (b): Reduced USAXS-XPCS data for uns-ACP composite collected at 105 °C at 0 min, 19 min, 38 min, 56 min, and 75 min after the start of heating. The standard deviation uncertainties are smaller than the symbols for the data points.

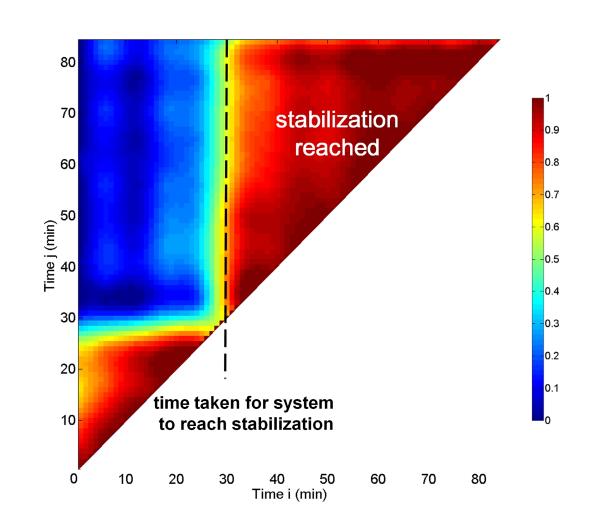
Following the procedure established in Section 3, we analyzed the structural dynamics of the composites using correlation coefficient maps. A simple example of a two-dimensional correlation coefficient map (Fig. 8) demonstrates its potential in assessing USAXS-XPCS data. We emphasize that this figure is for illustration purposes only. Its simplicity helps explain the correlation coefficient map representation and how dynamic time scales can be obtained from it. The USAXS-XPCS data were collected with a sil-ACP composite sample during cooling from 125 °C to 25 °C after being exposed to a temperature of 125 °C for ≈ 200 min. The correlation coefficients from every possible pair of USAXS-XPCS scan data have been calculated and presented. The X axis of the figure shows the start acquisition time of the i^th USAXS-XPCS scan, as in Eqn. 3, and the Y axis shows the start acquisition time of the j^th USAXS-XPCS scan. The color scale, displayed to the right of the figure, shows the magnitude of the correlation coefficient following Eqn. 3. The higher the value is, the more correlated the i^th and j^th scans are. A feature of this type of analysis is that as the sample approaches an equilibrium state, successive scans become highly correlated with each other. This is represented by the triangular red region towards the upper-right corner of the plot. Fig. 8 reveals that during cooling, the microstructure evolution of the sil-ACP composite resembles a two-level process. In the initial condition (0 to 30 min), the USAXS-XPCS patterns undergo little change. A structural change occurs at ≈ 30 min (dotted line). After this change, the USAXS-XPCS patterns become and remain highly correlated until the end of the measurement. The most likely explanation for the abrupt change is that it arises from a stick-slip type of relaxation process. This result illustrates how the dynamic time scale associated with a nonequilibrium local-microstructure change can be readily revealed by the USAXS-XPCS method.

Figure 8.

Correlation coefficient map for sil-ACP during cooling from 125 °C to 25 °C.

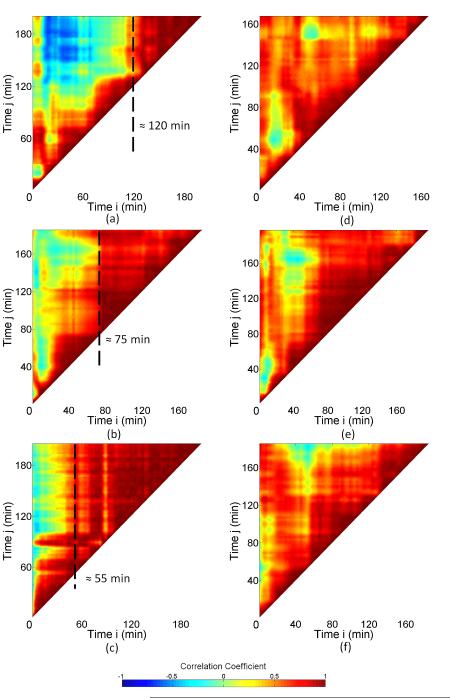
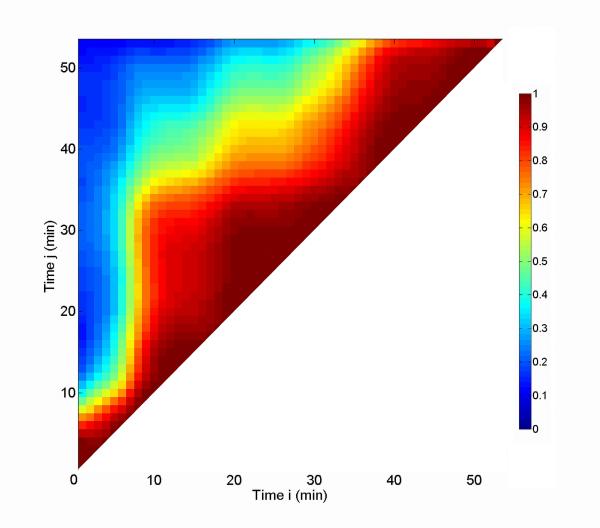
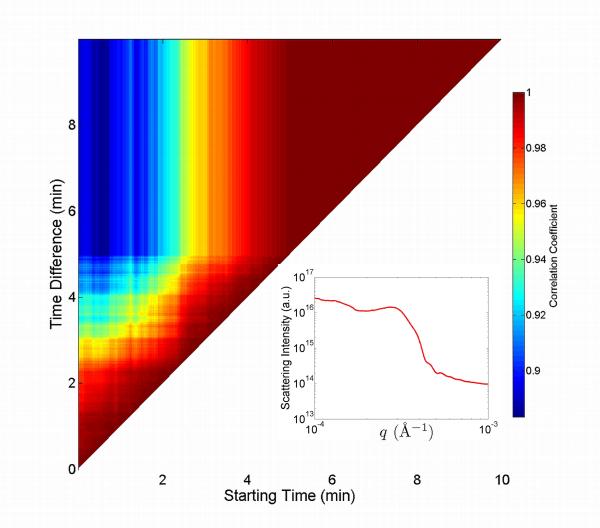
The correlation coefficient maps acquired for sil-ACP, and uns-ACP composites upon heating are more complicated. The correlation coefficient maps for uns-ACP and sil-ACP composites during separate isothermal anneals at 105 °C, 115 °C, and 125 °C are shown in Fig. 9. For comparison, a correlation coefficient map for uns-glass composite during annealing at 115 °C is shown in Fig. 10. For all these systems, it was found that the clearly defined two-level process of Fig. 8 was absent, and the dynamics are notably more complex. However, the stabilization “triangle” in the later stage of the heating process is still visible which suggests that equilibrium was reached before the end of each set of measurements. A close inspection of the uns-ACP results shows a dynamic time scale of ≈ 120 min, 75 min, and 55 min for the annealing processes at 105 °C , 115 °C, and 125 °C, respectively. These time scales are nearly double the time taken for the uns-glass composites to reach equilibrium under similar conditions (for example, ≈ 40 min at 115 °C, as shown in Fig. 10) . Considering that the rearrangement of the glass fillers in the uns-glass composite is largely thermally related, this result suggests that the uns-ACP fillers in uns-ACP composites may experience a more complicated process, which is controlled by determining factors other than thermal expansion of the polymer matrix and/or diffusion of the filler particles.

Figure 9.

Correlation coefficient maps for (a, b, c) uns-ACP and (d, e, f) sil-ACP composites during isothermal anneals at (a and d) 105 °C, ( b and e) 115 °C, and (c and f) 125 °C.

Figure 10.

Correlation coefficient map for an uns-glass composite during an isothermal anneal at 115 °C.

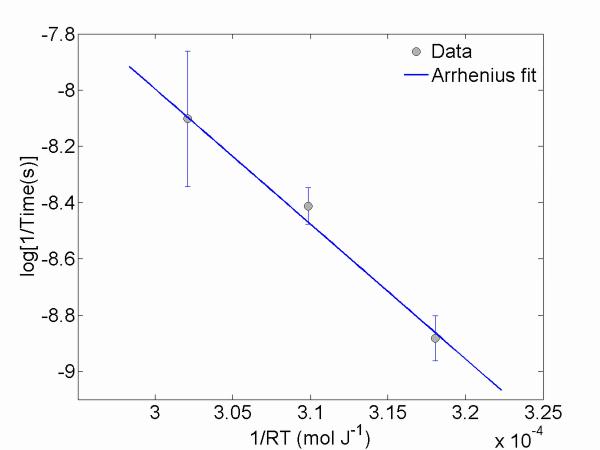
Fig. 9 (a) – (c) shows that the transition rates of the uns-ACP composites are strongly related to the temperature. Using these data, an Arrhenius plot, shown in Fig. 11, was derived to determine an activation energy of (54.34 ±10.90) kJ mol⁻¹. We note that this activation energy is slightly smaller than the activation energy ( ≈ 68 kJ mol⁻¹) acquired from an Arrhenius analysis of a solution-mediated ACP to HAP transformation⁴² and much smaller than the activation energy ( ≈ 453 kJ mol⁻¹) acquired from a thermally induced ACP-HAP transformation³⁷. As shown later, we suggest this activation energy is associated with a complex dehydration process within the composite ultimately related to the loss of water from the system, and we leave it to future work for a determination of its full physical significance.

Figure 11.

Arrhenius plot derived from Fig. 9 (a) – (c), yielding an activation energy for the water-loss related transformation of (54.34 ± 10.90) kJ mol⁻¹.

The correlation coefficient maps for sil-ACP composites are slightly different. The distinctively different states found in uns-ACP results, depicted by the blue region in Fig. 9 (a) – (c), are not seen, which suggests that the local microstructure evolves more slowly for sil-ACP composites. This also leads to a longer time for the USAXS-XPCS pattern to stabilize, as shown by a comparison of the correlation coefficient maps of uns-ACP and sil-ACP composites acquired at the same temperature. This phenomenon is anticipated, since the filler particles in the sil-ACP composites are coated with a silane group that both strengthens the filler’s bonding with the matrix and slows down the local structural rearrangements. Similar to the uns-ACP composites, the time taken for the USAXS-XPCS pattern to stabilize depends on the temperature – the higher the temperature, the shorter the dynamic time scale.

The USAXS-XPCS results, in contrast with the results of the bulk characterization methods, clearly reveal that slow, local structural changes occur in the ACP composites during heating at elevated temperatures and have identified the dynamic time scales in the cases of uns-ACP composites. The exact nature of this change, however, cannot be revealed by USAXS-XPCS alone because its sampling frequency does not allow retrieval of the real space configuration of the scattering objects.⁴³ Measurements with other techniques, therefore, are required to provide further insights into this change.

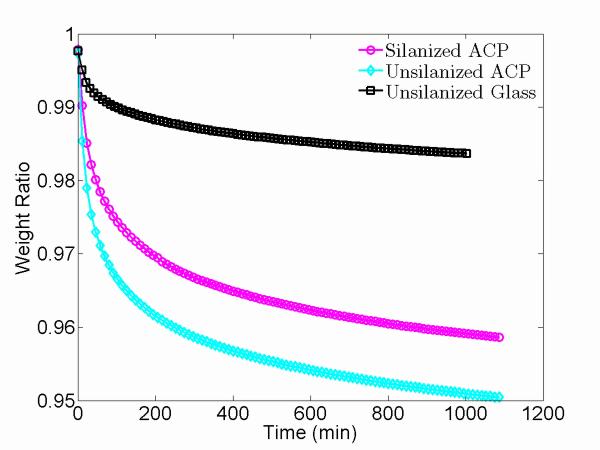
Given the known water-containing nature of the ACP composites, TGA measurements were performed on sil-ACP, uns-ACP, and uns-glass composites. In contrast to the ACP particles, which are hydrophilic, the glass fillers are hydrophobic⁸ and provide a baseline for the detection of water loss in ACP fillers. TGA results for sil-ACP, uns-ACP, and uns-glass composites are shown in Fig. 12. Previous studies have shown that for ACP fillers, the water content typically ranges from 14.5 % to 15.2 % by mass, which compares well with the water content reported for a typical, solution-matured ACP (15 % by mass ⁴⁴). While all three samples appear to lose water during the heating process, it is notable that the sil-ACP and uns-ACP composites lose significantly more than the uns-glass composite (1.4 % by mass). The mass loss in the uns-glass composites is attributed to water loss in the polymer matrix, as shown previously.⁸ Under the same conditions, the uns-ACP composite loses 4.9 % mass H₂O, more mass than the sil-ACP composite, which loses 4.1 % mass H₂O. Considering that the total s00.urface area of sil-ACP fillers is greater than that of the uns-ACP fillers due to their smaller primary particle sizes, this result suggests that the silanization surface coating must retard water loss. TGA screenings of the untreated uns- and sil-ACP fillers (in powder form) revealed a similar trend: the uns-ACP and sil-ACP fillers lost 7.0 % mass and 4.5 % mass H₂O, respectively, while the mass loss in the uns-glass fillers was approx. 0.1 %. Knowing that the uns-glass fillers contain very limited water, we can calculate the water-loss from the polymer matrix and ACP filler particles in the composites with the calculated resin:filler mass ratio. The estimated mass loss ratios of the fillers in the composites agree well with those obtained from the stand-alone fillers. This comparison is shown in Table 5. These results indicate the same trend for mass loss caused by water evaporation at temperatures above the liquid-gas transition point, i.e, upon heating, uns-ACP loses water more easily than sil-ACP. Additionally, the change in the scattering contrast factor, and hence in the scattering intensity in USAXS studies as shown in Fig. 5, due to loss of water from both ACP and the polymer matrix is calculated to be ≈ 2 %. In the present context, this is less than the stochastic uncertainties in the intensity calibration, and partially accounts for the fact that no detectable change was identified in the USAXS intensities before and after the heating process.

Figure 12.

TGA results for sil-ACP, uns-ACP, and uns-glass composites. Statistical uncertainties for the individual data points are smaller than the size of the symbols plotted.

Table 5.

Comparison of the TGA measurements in a flowing N₂ atmosphere in two different conditions: (1): Composite disk specimens annealed at 125 °C for 1000 min. (2): Filler powders heated to 600 °C at 20 °C/min. The uncertainties are shown in the parentheses.

Sample	Mass loss (%) Composites	Mass loss (%) Fillers (1)	Mass loss (%) Fillers (2)
Uns-glass	1.4(1)	NA	0.1(1)
Uns-ACP	4.9(1)	5.7(1)	7.0(1)
Sil-ACP	4.1(1)	3.8(1)	4.5(1)

More importantly, we note that the observed time scales for mass loss measured by TGA are close to those associated with the USAXS-XPCS correlation coefficient maps. This result strongly indicates that the water loss is correlated to local microstructure changes in the ACP composites, as revealed by USAXS-XPCS. Meanwhile, our FTIR results show a broadening of the phosphate peak near ≈ 600 cm⁻¹. Together, these results suggest the local changes in composite microstructure might be driven by densification of the ACP particles due to loss of water. However, neither the FTIR results nor our XRD results indicate any transformation of ACP to HAP. This is consistent with a previous NMR study of ACP particles in solution, which found no association between the removal of water per se and onset of the ACP-to-HAP transformation. 45 However, unlike the previous NMR study, the present FTIR results do indicate some changes in the phosphate environment, presumably associated with bound water loss.

Finally, we present the results of our simulation study of the effects of thermal expansion on the correlation coefficient map. An example correlation coefficient map simulation of silica spheres in Bis-GMA heated to 125 °C is shown in Fig. 13. The USAXS-XPCS pattern shows clear signs of speckles (inset) as anticipated, given the non-uniform distribution of the local electron density. The primary prediction in Fig. 13 is that thermal expansion has a relatively weak effect on the correlation coefficient, and only significantly affects the short time-scale dynamics. Fig. 13 and Fig. 10 (for starting times < 10 min) show the same behavior at short time scales, which is expected given that both figures illustrate similar physical processes. Fig. 10 also shows an additional slower process, which we believe is related to the water loss in the polymer resin. However, the simulation does not predict the complex variation of the correlation coefficient observed for both sil-ACP and uns-ACP composites over extended timescales. Thus, we surmise that this complex behavior does not originate solely from the thermal behavior of the composites, and must be attributed to other mechanisms such as local changes in the composite microstructure driven by water loss from the ACP filler particles and their presumed, consequent densification.

Figure 13.

Simulated correlation coefficient map for a SiO2 in BisGMA composite in thermal expansion.

Concluding Remarks

ACP- and glass-based polymer composites have been studied using static, bulk techniques and the recently developed USAXS-XCPS method which, based on the coherent interference of partially coherent X-rays, is a highly sensitive (interferometric) local structural probe. USAXS-XPCS bridges the gap in accessible q values (10⁻⁴ Å⁻¹ to 10⁻³ Å⁻¹) between conventional XPCS and dynamic light scattering, and is capable of monitoring equilibrium dynamics in a point detection mode and non-equilibrium dynamics in a scanning mode.

While bulk techniques such as XRD, FTIR, and USAXS cannot offer concrete evidence of structural variation of the composites upon heating, USAXS-XPCS, taking advantage of the statistical correlation coefficient and a data-reduction procedure established for this type of USAXS-XPCS data, unambiguously reveals the subtle changes associated with the changing local structure of the composites. The observed dynamic time scales show that, on heating to the same temperature and holding under isothermal conditions, both sil-ACP and uns-ACP composites require more time than glass composites to reach equilibrium, and it takes a longer time for sil-ACP composites than for uns-ACP composites to do so. The dynamic time-scales of the ACP composites are corroborated by the time-scales observed in TGA measurements, which show substantial mass loss as heating continues. This collective set of results suggests that as water is removed from the ACP fillers, the local microstructure of the ACP composites changes, which directly indicates that the presence of water affects the detailed arrangements of ACP. The prolonged dynamic time scale observed in sil-ACP composites, when compared with that in uns-ACP composites, is consistent with this scenario as silanization introduces a surface layer around the ACP filler particles and delays the release of water. The lack of crystalline features in XRD profiles shows that the ACP particles remain amorphous despite prolonged heating at the temperatures used in these studies, but we hypothesize that water release is a prelude to the known ACP to HAP transformation.

We envisage future USAXS-XPCS studies could elucidate the role of water in the formation of ACP. It is known that in a solution-medicated, pH-dependent environment, ACP-HAP transformation occurs on a time scale similar to those observed in our measurements. Monitoring this process would allow the release of water to be better characterized as ACP converts to a crystalline form. Alternatively, the structural changes in ACP particles could be monitored without the presence of either polymer resins. The suggested transient nature of ACP particles then could be more directly interrogated.

In the context of the present work, we conclude from the USAXS-XPCS and TGA studies that significant water loss from ACP can occur with associated densification of the ACP particles, but without a significant amorphous-to-crystalline (ACP-to-HAP) conversion detectable by XRD or FTIR.

A simple simulation was performed to probe the role of the thermal expansion on the observed dynamics. While relatively crude, it clearly shows features that resemble the experimental results for both glass-composites on heating and sil-ACP composites on cooling. These similarities confirm that thermal behavior alone cannot account for the more complex dynamics observed in sil-ACP and uns-ACP composites during heating. To address these issues in detail, finite element modeling would be required and is currently under way.

We note that it is a fundamental challenge to characterize matter away from equilibrium states where static approaches may not apply. To understand non-equilibrium behavior, the challenges associated with connecting theory to measurement across many length and time scales must be addressed. USAXS-XPCS offers a unique tool for following slow dynamics in disordered materials albeit with limited q-range and time resolution. However, it can be combined with more conventional XPCS and SAXS methods and it is our hope that USAXS-XPCS will help further the understanding of the non-equilibrium dynamic evolution of a wide variety of perturbed material systems as they progress towards equilibrium. As we have sought to demonstrate here, we believe that biomedical materials research could benefit greatly from this approach.