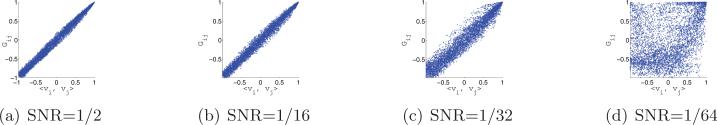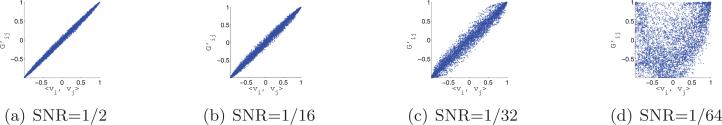Viewing Angle Classification of Cryo-Electron Microscopy Images Using Eigenvectors

Abstract

The cryo-electron microscopy (cryo-EM) reconstruction problem is to find the three-dimensional structure of a macromolecule given noisy versions of its two-dimensional projection images at unknown random directions. We introduce a new algorithm for identifying noisy cryo-EM images of nearby viewing angles. This identification is an important first step in three-dimensional structure determination of macromolecules from cryo-EM, because once identified, these images can be rotationally aligned and averaged to produce “class averages” of better quality. The main advantage of our algorithm is its extreme robustness to noise. The algorithm is also very efficient in terms of running time and memory requirements, because it is based on the computation of the top few eigenvectors of a specially designed sparse Hermitian matrix. These advantages are demonstrated in numerous numerical experiments.

1. Introduction

In this paper we address the class averaging problem in cryo-electron microscopy (cryo-EM) [10]. The goal in cryo-EM is to determine three-dimensional (3D) macromolecular structures from noisy projection images taken by an electron microscope at unknown random orientations, i.e., a random computational tomography (CT). Determining 3D macromolecular structures for large biological molecules remains vitally important, as witnessed, for example, by the 2003 Nobel Prize in Chemistry, co-awarded to MacKinnon for resolving the 3D structure of the Shaker K⁺ channel protein [8, 17], and by the 2009 Nobel Prize in Chemistry, awarded to Ramakrishnan, Steitz, and Yonath for studies of the structure and function of the ribosome. The standard procedure for structure determination of large molecules is X-ray crystallography. The challenge in this method is often more in the crystallization itself than in the interpretation of the X-ray results, since many large proteins have so far withstood all attempts to crystallize them.

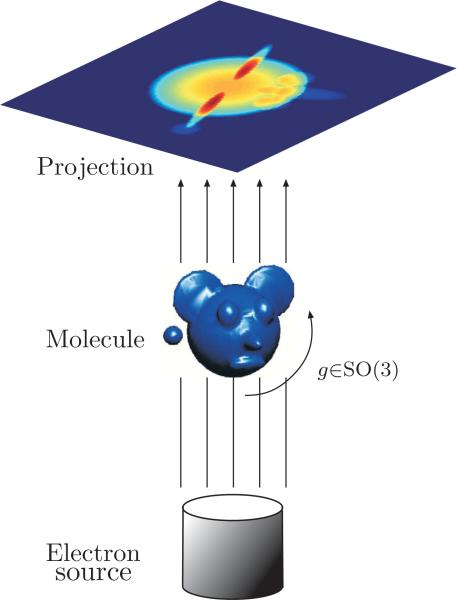
In cryo-EM, an alternative to X-ray crystallography, the sample of macromolecules is rapidly frozen in an ice layer so thin that their tomographic projections are typically disjoint; this seems the most promising alternative for molecules that defy crystallization. The cryo-EM imaging process produces a large collection of tomographic projections of the same molecule, corresponding to different and unknown projection orientations. The goal is to reconstruct the 3D structure of the molecule from such unlabeled projection images, where data sets typically range from 10⁴ to 10⁵ projection images whose size is roughly 100 × 100 pixels. The intensity of the pixels in a given projection image is proportional to the line integrals of the electric potential induced by the molecule along the path of the imaging electrons (see Figure 1). The highly intense electron beam destroys the frozen molecule, and it is therefore impractical to image the same molecule at known different directions as in the case of classical CT. In other words, a single molecule can be imaged only once, rendering an extremely low signal-to-noise ratio (SNR) for the images (see Figure 2 for a sample of real microscope images), mostly due to shot noise induced by the maximal allowed electron dose (other sources of noise include the varying thickness of the ice layer and partial knowledge of the contrast transfer function of the microscope). In the basic homogeneity setting considered hereafter, all imaged molecules are assumed to have the exact same structure; they differ only by their spatial rotation. Every image is a projection of the same molecule from an unknown random direction, and the cryo-EM problem is to find the 3D structure of the molecule from a collection of noisy projection images.

Figure 1.

Schematic drawing of the imaging process: Every projection image corresponds to some unknown 3D rotation of the unknown molecule.

Figure 2.

A collection of four real electron microscope images of the E. coli 50S ribosomal subunit.

The rotation group SO(3) is the group of all orientation preserving orthogonal transformations about the origin of the 3D Euclidean space ${\mathbb{R}}^3$ under the operation of composition. Any 3D rotation can be expressed using a 3 × 3 orthogonal matrix R:

$$R=\left(\begin{array}{ccc}\hfill \mid \hfill & \hfill \mid \hfill & \hfill \mid \hfill \\ \hfill R^1\hfill & \hfill R^2\hfill & \hfill R^3\hfill \\ \hfill \mid \hfill & \hfill \mid \hfill & \hfill \mid \hfill \end{array}\right)$$

satisfying

$$R{R}^T=R^{T}R=I,\text{det}R=1,$$

where I is the 3×3 identity matrix. The column vectors R¹, R², R³ of R form an orthonormal basis to ${\mathbb{R}}^3$.

To each projection image P there corresponds a 3×3 unknown rotation matrix R describing its orientation (see Figure 1). Excluding the contribution of noise, the intensity P(x, y) of the pixel located at (x, y) in the image plane corresponds to the line integral of the electric potential induced by the molecule along the path of the imaging electrons; that is,

$$P(x,y)={\int }_{-\infty }^{\infty }\varphi (x{R}^1+y{R}^2+z{R}^3)dz,$$ (1.1)

where $\varphi :{\mathbb{R}}^3\mapsto \mathbb{R}$ is the electric potential of the molecule in some fixed “laboratory” coordinate system. The projection operator (1.1) is also known as the X-ray transform [19].

We therefore identify the third column R³ of R as the imaging direction, also known as the viewing angle of the molecule. We will often refer to the viewing angle of R as v; that is, $v:\mathit{SO}\left(3\right)\mapsto {\mathbb{R}}^3$ is given by v = v(R) = R³. The viewing angle v can be realized as a point on S² (the unit sphere in ${\mathbb{R}}^3$) and can therefore be described using two parameters.

The first two columns R¹ and R² form an orthonormal basis for the plane in ${\mathbb{R}}^3$ perpendicular to the viewing angle v. All clean projection images of the molecule that share the same viewing angle v look the same up to some in-plane rotation. That is, if R_i and R_j are two rotations with the same viewing angle v(R_i) = v(R_j), then $R_i^1$, $R_i^2$ and $R_j^1$, $R_j^2$ are two orthonormal bases for the same plane and the rotation matrix $R_i^{-1},R_j$ has the form

$$R_i^{-1}{R}_j=\left(\begin{array}{ccc}\hfill \text{cos}{\theta }_{ij}\hfill & \hfill -\text{sin}{\theta }_{ij}\hfill & \hfill 0\hfill \\ \hfill \text{sin}{\theta }_{ij}\hfill & \hfill \text{cos}{\theta }_{ij}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right),$$ (1.2)

where θ_ij ∈ [0, 2π) is the angle in which we have to in-plane rotate image j in the counterclockwise direction in order for it to be aligned with image i. On the other hand, two rotations with opposite viewing angles v(R_i) = −v(R_j) give rise to two projection images that are the same after reflection (mirroring) and some in-plane rotation.

As projection images in cryo-EM have extremely low SNRs, a crucial initial step in all reconstruction methods is “class averaging” [10]. Class averaging is the grouping of a large data set of n noisy raw projection images P₁, …, P_n into clusters, such that images within a single cluster have similar viewing angles (it is possible to artificially double the number of projection images by including all mirrored images). Averaging rotationally aligned noisy images within each cluster results in “class averages”; these are images that enjoy a higher SNR and are used in later cryo-EM procedures such as the angular reconstitution procedure [27] that requires better quality images. Finding consistent class averages is challenging due to the high level of noise in the raw images as well as the large size of the image data set. A sketch of the class averaging procedure is shown in Figure 3.

Figure 3.

The class averaging problem is to find, align, and average images with similar viewing angles: (a) a clean simulated projection image of the ribosomal subunit generated from its known density map; (b) noisy instance of (a), denoted P_i, obtained by the addition of white Gaussian noise. For the simulated images we chose the SNR to be higher than that of experimental images in order for image features to be clearly visible; (c) noisy projection, denoted P_j, of the subunit taken at the same viewing angle but with a different in-plane rotation. The in-plane rotation angle is θ_ij = 3π/2, because image P_j needs to be rotated by π/2 in the clockwise direction in order to be aligned with P_i (see also text following (1.3)); (d) averaging the noisy images (b) and (c) after in-plane rotational alignment. The class average of the two images has a higher SNR than that of the noisy images (b) and (c), and it has better similarity to the clean image (a).

Penczek, Zhu, and Frank [20] introduced the rotationally invariant K-means clustering procedure to identify images that have similar viewing angles. Their invariant distance d_ij between image P_i and image P_j is defined as the Euclidean distance between the images when they are optimally aligned with respect to in-plane rotations (assuming the images are centered):

$$d_{ij}=\underset{\theta \in [0,2\pi )}{\text{min}}\Vert P_i-R\left(\theta \right)P_j\Vert ,$$ (1.3)

where R(θ) is the rotation operator of an image by an angle θ in the counterclockwise direction. Prior to computing the invariant distances of (1.3), a common practice is to center all images by correlating them with their total average $\frac{1}{n}{\Sigma }_{i=1}^n{P}_i$, which is approximately radial (i.e., has little angular variation) due to the randomness in the rotations. The resulting centers usually miss the true centers by only a few pixels (as can be validated in simulations during the refinement procedure). Therefore, as in [20], we also choose to focus first on the more challenging problem of rotational alignment by assuming that the images are properly centered. The problem of translational alignment will be considered elsewhere. Other methods for class averaging are reviewed in [28].

It is worth noting that the specific choice of metric to measure proximity between images can make a big difference in class averaging. The cross-correlation and Euclidean distance (1.3) are by no means optimal measures of proximity. In practice, it is common to denoise the images prior to computing their pairwise distances. A popular smoothing scheme is to convolve the images with a Gaussian kernel, and other linear and nonlinear filters are also used. Although the discussion which follows is independent of the particular choice of filter or distance metric, we stress again that filtering can have a dramatic effect on finding meaningful class averages.

The invariant distance (1.3) is invariant to in-plane rotations and as such it induces a metric on the viewing angle space S². The invariant distance between noisy images that share the same viewing angle (with perhaps a different in-plane rotation) is expected to be small. Ideally, all neighboring images of some reference image P_i in a small invariant distance ball centered at P_i should have similar viewing angles, and averaging such neighboring images (after proper rotational alignment) would amplify the signal and diminish the noise.

Unfortunately, due to the low SNR, it often happens that two images of completely different viewing angles have a small invariant distance. This can happen when the realizations of the noise in the two images match well for some random in-plane rotational angle, leading to spurious neighbor identification. Therefore, averaging the nearest neighbor images can sometimes yield a poor estimate of the true signal in the reference image.

Clustering algorithms, such as the K-means algorithm, perform much better than this naive nearest neighbor averaging, because they take into account all pairwise distances, not just distances to the reference image. Such clustering procedures are based on the philosophy that images that share a similar viewing angle with the reference image are expected to have a small invariant distance not only to the reference image but also to all other images with similar viewing angles. This observation was utilized in the rotationally invariant K-means clustering algorithm [20]. Such clustering algorithms make it harder for spurious neighbors to sneak their way into the neighborhood. Still, noise is our enemy, and the rotationally invariant K-means clustering algorithm may suffer from misidentifications at the low SNR values present in experimental data.

Is it possible to further improve the detection of neighboring images at even lower SNR values? In this paper we provide a positive answer to this question. First, we note that the rotationally invariant distance neglects an important piece of information, namely, the optimal angle that realizes the best rotational alignment in (1.3). Second, we observe that these optimal rotation angles must satisfy a global system of consistency relations, namely, that if three projection images correspond to similar viewing angles, then the three optimal rotational angles should add up to 0 modulo 2π. Based on these observations, we use the optimal in-plane rotation angles to construct a sparse n × n Hermitian matrix, which we call “the class averaging matrix,” and show how to identify nearby viewing directions from the top three eigenvectors of the matrix.

The main advantage of the algorithm presented here is that it successfully identifies images with nearby viewing directions even in the presence of high levels of noise in the images. For such high levels of noise, it is possible for pairs of images with viewing angles that are far apart to have relatively small rotationally invariant distances. Our algorithm is extremely robust to such outliers, as we demonstrate both theoretically and in various numerical experiments. This robustness to outliers is explained using random matrix theory, similar to the way we showed robustness of our 3D eigenvector reconstruction algorithm from common lines [24]. Another advantage of the algorithm is that it has a low computational complexity as it requires only the computation of the top three eigenvectors of the class averaging matrix, which is a sparse matrix.

In [23] we presented an algorithm for estimating angles from noisy measurements of their offsets modulo 2π using the top eigenvector of a Hermitian matrix constructed in exactly the same way the class averaging matrix is constructed. The reason why three eigenvectors (instead of one) are needed here is due to the special topology of the sphere S² as rendered in the “hairy ball” theorem that says that a continuous tangent vector field to the sphere must vanish at some point. We also conducted numerical experiments that demonstrate how the identification of nearby viewing directions can be improved by using more than three eigenvectors. Finally, we show that the class averaging matrix is a discretization of a local version of the parallel transport operator on the sphere. This interpretation leads to a complete understanding of the spectrum of the class averaging matrix and to a rigorous proof of the admissibility (correctness) of the algorithm presented in this paper. The complete spectral analysis will be presented in a separate publication [13].

2. Small-world graph on S², triplets consistency, and angular synchronization

The purpose of this section is to motivate the construction of the class averaging matrix. We provide here the intuition that leads to the construction of the class averaging matrix, whose mathematical meaning will become apparent only in section 4.

As mentioned earlier, the information in the optimal in-plane rotation angles has yet to be utilized in existing class averaging algorithms. We incorporate this additional information as follows. When computing the optimal alignment of images P_i and P_j and their invariant distance d_ij, we also record the rotation angle θ_ij that brings the distance between the two images to a minimum,

$${\theta }_{ij}=\underset{\theta \in [0,2\pi )}{\text{argmin}}\Vert P_i-R\left(\theta \right)P_j\Vert ,i,j=1,\dots ,n.$$ (2.1)

Note that

$${\theta }_{ij}=-{\theta }_{ij}\text{mod}2\pi ,$$ (2.2)

as the optimal rotation from P_j to P_i is in the opposite direction as that from P_i to P_j.

We assume that there is a unique optimal in-plane rotation angle θ_ij for which the minimum in (2.1) is attained. Note that this assumption excludes, for example, projection images of symmetric molecules when the viewing direction coincides with the symmetry axis, and perhaps other projection images are also excluded. Note that if P_i and P_j are clean images having the same viewing angle v_i = v_j, then the optimal in-plane rotation angle θ_ij computed in the optimization procedure (2.1) agrees with the angle θ_ij introduced in (1.2). In that sense, the computed angles θ_ij provide additional information about the unknown rotation matrices R₁, …, R_n.

In practice, however, we cannot expect two projection images to have exactly the same viewing angle. Still, we may assume that the molecule is “nice” enough¹ such that projection images that correspond to nearby viewing angles would look similar (up to an in-plane rotation). In such cases, it is reasonable to assume that the optimal in-plane rotation angle θ_ij computed in (2.1) provides a good approximation to the angle ${\tilde{\theta }}_{ij}$ that “aligns” the orthonormal bases for the planes² $v_i^{\perp }$, $v_j^{\perp }$, given by the vectors $R_i^1$, $R_i^2$ and $R_j^1$, $R_j^2$, respectively. In other words, for clean images, it is expected that a small distance between v_i and v_j would imply that θ_ij approximates the angle ${\tilde{\theta }}_{ij}$ given by

$${\tilde{\theta }}_{ij}=\underset{\theta \in [0,2\pi )}{\text{argmin}}{\Vert R_i\rho \left(\theta \right)-R_j\Vert }_F,$$ (2.3)

where

$$\rho \left(\theta \right)=\left(\begin{array}{ccc}\hfill \text{cos}\theta \hfill & \hfill -\text{sin}\theta \hfill & \hfill 0\hfill \\ \hfill \text{sin}\theta \hfill & \hfill \text{cos}\theta \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right)$$ (2.4)

and ∥·∥_F is the Frobenius norm of the matrix (square root of the sum of its squared elements). The reader may verify that ${\tilde{\theta }}_{ij}$ satisfies

$$\text{cos}{\tilde{\theta }}_{ij}=\frac{{\left(R_i^{-1}{R}_j\right)}_{11}+{\left(R_i^{-1}{R}_j\right)}_{22}}{\sqrt{{[{\left(R_i^{-1}{R}_j\right)}_{11}+{\left(R_i^{-1}{R}_j\right)}_{22}]}^2+{[{\left(R_i^{-1}{R}_j\right)}_{21}-{\left(R_i^{-1}{R}_j\right)}_{12}]}^2}},$$ (2.5)

$$\text{sin}{\tilde{\theta }}_{ij}=\frac{{\left(R_i^{-1}{R}_j\right)}_{21}-{\left(R_i^{-1}{R}_j\right)}_{12}}{\sqrt{{[{\left(R_i^{-1}{R}_j\right)}_{11}+{\left(R_i^{-1}{R}_j\right)}_{22}]}^2+{[{\left(R_i^{-1}{R}_j\right)}_{21}-{\left(R_i^{-1}{R}_j\right)}_{12}]}^2}},$$ (2.6)

in accordance with (1.2) even when v_i differs from v_j. Thus, computing θ_ij provides indispensable information about the unknown rotations R₁, …, R_n.

By making a histogram of all $\left(\begin{array}{c}\hfill n\hfill \\ \hfill 2\hfill \end{array}\right)$ distances d_ij, one can choose some threshold value ε, such that d_ij ≤ ε is indicative that perhaps P_i and P_j have nearby viewing angles. The threshold ε defines an undirected graph G = (V, E) with n vertices corresponding to the projection images, with an edge between nodes i and j iff their invariant distance is smaller than ε:

$$\{i,j\}\in E\iff d_{ij}\le \epsilon .$$ (2.7)

Alternatively, an undirected graph may be constructed from the identification of nearest neighbors, such that {i, j} ∈ E iff i is one of the N nearest neighbors of j or j is one of the N nearest neighbors of i, where N ≪ n is a fixed parameter. Yet another possibility is to take the intersection instead of the union; i.e., {i, j} ∈ E iff i is one of the N nearest neighbors of j and j is one the N nearest neighbors of i.

Either way, in an ideal noiseless world, the topology of the graph is that of S²; for each vertex there corresponds a viewing angle, which is a unit vector in three-space realized as a point on the sphere. If all invariant distances were trustworthy such that small distances imply similar viewing angles, then the edges of G would link neighboring points on S². The drawing of such a graph in 3D space would show scattered points (vertices) on the sphere connected by short chords (edges). The experimental world, however, is far from ideal and is ruled by noise, giving rise to false edges that shortcut the sphere by long chords. Such graphs are known as “small-world” graphs [29], a popular model to describe social network phenomena such as the six degrees of separation: our social network consists of people living in our own town (neighboring edges), but also some other family and friends who live across the world (shortcut edges). Planar drawings of a ring graph and its corresponding small-world graph are given in Figure 4.

Figure 4.

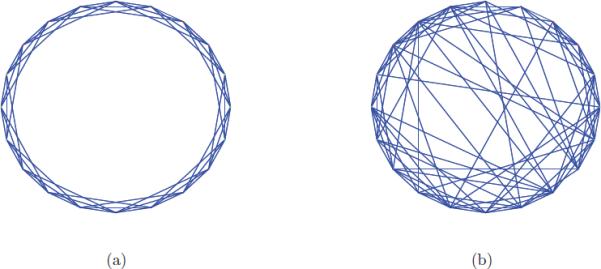
(a) A ring graph with 20 vertices each of which is connected to its six nearest neighbors with short edges; (b) a small-world graph obtained by randomly rewiring the edges of the ring graph with probability 0.2 leading to about 20% of shortcut edges.

Can we tell the good edges (short chords) from the bad edges (long chords)? It is possible to denoise small-world graphs based on the fact that they have many more “triangles” than random graphs: two images P_i and P_j that have nearby viewing angles should have common neighboring images P_k whose viewing angles are close to theirs. All three edges {i, j}, {j, k}, and {k, i} are in E forming a triangle (i, j, k). On the other hand, shortcut edges are not expected to be sides of as many triangles. This “cliquishness” property of small-world graphs was used by Goldberg and Roth [11] to denoise protein-protein interaction maps by thresholding edges that appear in only a few triangles.

In the class averaging problem of cryo-EM, we can further test for the consistency of the triangles. Indeed, if the three images P_i, P_j, and P_k share the same viewing angle, then the three corresponding rotation angles θ_ij, θ_jk, and θ_ki must satisfy

$${\theta }_{ij}+{\theta }_{jk}+{\theta }_{ki}=0\text{mod}2\pi .$$ (2.8)

because rotating first from P_i to P_j, followed by a rotation from P_j to P_k, and finally a rotation from P_k to P_i together complete a full circle. Equation (2.8) is a consistency relation that enables us to detect image triplets with similar viewing angles and to identify good triangles. Similarly, we may write consistency relations that involve four or more images.

At first (but incorrect³) inspection, the triplet consistency relation seems to be a byproduct of an underlying angular synchronization problem [23]. If all projection images can be initially rotated such that they are optimally rotationally aligned, then we can let θ_i be the rotation angle of image P_i that brings it in sync with all other images. The mutual rotation angles θ_ij should satisfy the difference equations

$${\theta }_i-{\theta }_j={\theta }_{ij}\text{mod}2\pi \text{for}(i,j)\in E,$$ (2.9)

from which the consistency relation (2.8) immediately follows:

$${\theta }_{ij}+{\theta }_{jk}+{\theta }_{ki}={\theta }_i-{\theta }_j+{\theta }_j-{\theta }_k+{\theta }_k-{\theta }_i=0\text{mod}2\pi .$$

In [23] we introduced a robust and efficient synchronization algorithm for estimating the angles θ₁, …, θ_n from noisy offset measurements of the form (2.9). The first step of the synchronization algorithm is to construct an n × n Hermitian matrix H as

$$H_{ij}=\{\begin{array}{cc}{e}^{ı{\theta }_{ij}},\hfill & \{i,j\}\in E,\hfill \\ 0,\hfill & \{i,j\}\notin E,\hfill \end{array}\phantom{\}}$$ (2.10)

where $\mathcal{i}=\sqrt{-1}$ The matrix H is Hermitian, i.e., $H_{ij}={\stackrel{‒}{H}}_{ji}$, because the offsets are skew-symmetric; i.e., θ_ij = −θ_ji mod 2π. As H is Hermitian, its eigenvalues are real. The second step of the synchronization algorithm is to compute the top eigenvector v₁ of H with maximal eigenvalue, and to derive an estimator ${\widehat{\theta }}_1,\dots ,{\widehat{\theta }}_n$ for the angles in terms of this top eigenvector as

$$e^{ı{\widehat{\theta }}_i}=\frac{v_1\left(i\right)}{\mid v_1\left(i\right)\mid },i=1,\dots ,n.$$ (2.11)

The motivation and analysis of this eigenvector-based synchronization algorithm are detailed in [23].

3. Hairy ball theorem

Unfortunately, the top eigenvector of H constructed with the offset angles given in (2.1) does not provide rotation angles that would bring all the projection images in sync. This is due to the fact that such rotation angles simply do not exist! That is, there is no way to rotate all images such that every pair of images with nearby viewing angles would be rotationally aligned. This somewhat surprising fact is a consequence of the topology of S² and, more specifically, a mathematical theorem known as the hairy ball theorem.

The hairy ball theorem says that a continuous tangent vector field to S² must vanish at some point on the sphere. In other words, if f is a continuous function that assigns a vector in ${\mathbb{R}}^3$ to every point v on the sphere such that f(v) is always tangent to the sphere at v, then there is at least one v ∈ S² such that f(v) = 0. The theorem attests to the fact that it is impossible to comb a hairy (spherical) cat without creating a cowlick. For example, consider the tangent vector field f given by

$$f\left(v\right)=v\times \left(\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 1\hfill \end{array}\right)=\left(\begin{array}{c}\hfill y\hfill \\ \hfill -x\hfill \\ \hfill 0\hfill \end{array}\right)\text{for}v=\left(\begin{array}{c}\hfill x\hfill \\ \hfill y\hfill \\ \hfill z\hfill \end{array}\right).$$ (3.1)

The tangent vector field f is continuous but vanishes at the north and south poles ±(0, 0, 1). The normalized tangent vector field

$$\frac{f}{\Vert f\Vert }=\frac{1}{\sqrt{x^2+y^2}}f=\frac{1}{\sqrt{1-z^2}}f$$

is discontinuous at the poles z = ±1. The hairy ball theorem implies that any attempt to find a nonvanishing continuous tangent vector field to the sphere would ultimately fail. An elementary proof of the theorem can be found in [18].

We now explain the way the hairy ball theorem relates to the rotational alignment problem of the projection images. Each projection image P whose corresponding rotation is R can be viewed as a tangent plane to S² at the viewing direction v = v(R) = R³. The first two columns of R, namely, R¹ and R², are vectors in ${\mathbb{R}}^3$ that form an orthogonal basis for the tangent plane. Together with the imaging direction v they make an orthogonal basis of ${\mathbb{R}}^3$. An in-plane rotation of the projection image can thus be viewed as changing the basis vectors R¹ and R² while keeping v fixed. A successful rotational alignment of all projection images means that we can choose orthogonal bases to all tangent planes such that the basis vectors vary smoothly from one tangent plane to the other. However, this is a contradiction to the hairy ball theorem! We conclude that the rotational alignment of all images cannot be considered as an angular synchronization problem, because there does not exist a set of angles θ₁, …, θ_n such that θ_ij = θ_i − θ_j, not even approximately. We refer the reader to Appendix B for a discussion about the relevance of the hairy ball theorem in the discrete case of a finite number of images.

4. Parallel transport and spectral properties of the class averaging matrix

We note that (2.8) can hold (approximately) without (2.9). So, instead of getting too pessimistic from the hairy ball theorem, we observe that the matrix H is a well-defined Hermitian matrix, and nothing prevents us from computing its eigenvectors and eigenvalues. In fact, we expect the eigenvectors of H to somehow capture the consistency relation (2.8) and all higher-order consistency constraints that correspond to cycles longer than three. The question is whether or not the eigenvectors of H are meaningful in the sense that they will allow us to identify images with nearby viewing angles, and if so, how?

We show that there is indeed a relatively simple algorithm that successfully identifies images with nearby viewing directions using the top three (or more) eigenvectors of H. The underpinning of the algorithm is the connection between the matrix H and the parallel transport operator on the sphere. To that end, consider the case in which the underlying graph is a neighborhood graph on S², without any shortcut edges.⁴ More specifically, we assume that the neighborhood of every vertex corresponds to a small spherical cap with an opening angle α; that is, if v₁, v₂ ∈ S² are two different viewing angles, then there is an edge between v₁ and v₂ iff 〈v₁, v₂〉 > cos α. We denote the resulting matrix by H^clean to emphasize that there are no shortcut edges, which will be the case if the matrix is constructed from clean projection images that contain no noise.

As mentioned earlier, we may think of a projection image P with corresponding rotation matrix R as living on the tangent plane to the sphere at the viewing angle v = R³. The tangent plane at the point v can be identified with the standard Euclidean plane ${\mathbb{R}}^2$ using the first two columns R¹, R² of R. Let us denote⁵ this copy of ${\mathbb{R}}^2$ by T_R. In addition, we note that T_R can be further identified with $\mathbb{C}$: any vector $\left(\begin{array}{c}\hfill a\hfill \\ \hfill b\hfill \end{array}\right)\in T_R$ is identified with the complex number $z=a+\mathcal{i}b\in \mathbb{C}$. This complex structure is the one induced from the orientation defined by the viewing angle v.

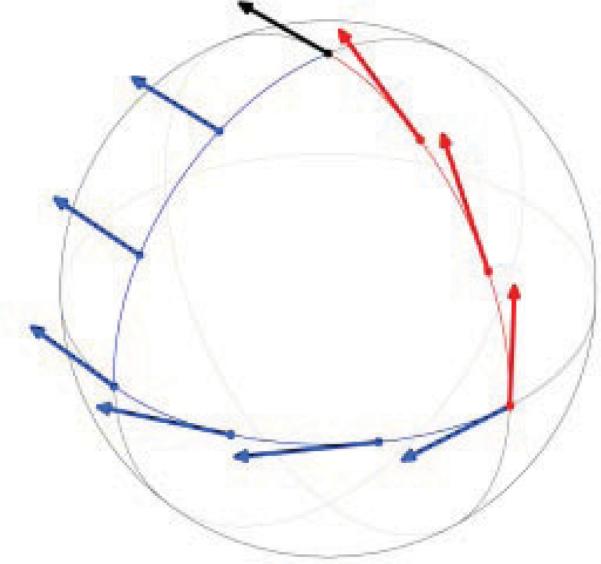
Between any two nonantipodal points v_i, v_j ∈ S² there is a unique geodesic line (a great circle) that connects them. We can slide any vector tangent to the sphere at v_j along this geodesic line in such a way that the sliding vector remains tangent to the sphere until it reaches the point v_i, where it becomes a tangent vector to the sphere at v_i. During this transportation, we make sure that the angle that the tangent vector makes with the geodesic remains constant. The transportation that takes vectors in T_Rj to vectors in T_Ri is a linear transformation denoted by ${\mathcal{T}}_{R_i,R_j}:T_{R_j}\mapsto T_{R_i}$ and is known in differential geometry as the parallel transport operator on the sphere [7, Chapter 4] (see Figure 5).

Figure 5.

Illustration of the parallel transport operator on the sphere (taken from http://en.wikipedia.org/wiki/Connection_(mathematics)).

The main observation is that whenever two projection images P_i and P_j have nearby viewing angles v_i and v_j satisfying 〈v_i, v_j〉 > cos α, the matrix element $H_{ij}^{\mathit{clean}}=e^{\mathcal{i}{\theta }_{ij}}$ is an approximation to the parallel transport operator ${\mathcal{T}}_{R_i,R_j}:T_{R_j}\mapsto T_{R_i}$, viewed as an operator from $\mathbb{C}$ to $\mathbb{C}$. That is, if z_j ∈ T_Rj, then $e^{\mathcal{i}{\theta }_{ij}}{z}_j\approx {\mathcal{T}}_{R_i,R_j}{z}_j\in T_{R_i}$ (in Appendix A.5 we give the explicit formula of the parallel transport operator on the sphere and show that it coincides with the rotation implied by the optimization procedure (2.3)).

This implies that the limiting class averaging matrix $\mathcal{H}={\lim }_{n\to \infty }\frac{1}{n}{H}^{\mathit{clean}}$ in the limit of an infinite number of clean images whose viewing angles are independently drawn from the uniform distribution on S² is a local version of the parallel transport operator $\mathcal{T}$ on the sphere. The parallel transport operator takes tangent vector fields to the sphere to tangent vector fields on the sphere. The (global) parallel transport operator $\mathcal{T}$ can be written in terms of the following integral over SO(3):

$$\left(\mathcal{T}f\right)\left(R\right)={\int }_{SO\left(3\right)}{\mathcal{T}}_{R,U}f\left(U\right)dU,$$ (4.1)

where dU is the uniform (invariant Haar) measure over SO(3), and f is any complex-valued function on SO(3) satisfying f(R) ∈ T_R for all R ∈ SO(3). We define the local parallel transport operator ${\mathcal{T}}_h$ by the integral

$$\left({\mathcal{T}}_{h}f\right)\left(R\right)={\int }_{U\in SO\left(3\right):\langle v\left(U\right),v\left(R\right)\rangle >1-h}{\mathcal{T}}_{R,U}f\left(U\right)dU,$$ (4.2)

where h = 1 − cos α ∈ [0, 2] and α is the opening angle of the spherical cap. To conclude, we obtain

$$\mathcal{H}={\mathcal{T}}_h.$$ (4.3)

In this regard, the matrix H^clean should be considered as a discretization of ${\mathcal{T}}_h$. Note that from the experimental data obtained from rotationally aligning the images we are only able to extract (a discretization of) the local parallel transport operator. This is due to the fact that we do not know at this point how to transport vectors between projection images (tangent planes) whose viewing angles are far apart, because the angle θ_ij obtained from the rotational alignment (2.1) of dissimilar images is meaningless in such cases in the sense that it has nothing to do with parallel transportation.

It follows that the spectral properties of the matrix H^clean are governed by the spectral properties of the operator ${\mathcal{T}}_h$. We now state without proof⁶ a few results concerning the spectrum of ${\mathcal{T}}_h$.

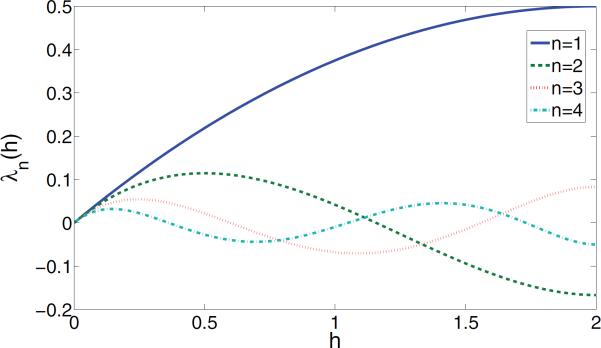
The first result states that the multiplicities of the eigenvalues λ_n(h) of ${\mathcal{T}}_h$ are 3, 5, 7, 9, …, that is, the following:

$$\text{The multiplicity of}{\lambda }_n\left(h\right)\text{is}2n+1,n=1,2,\dots .$$

Note that the multiplicity 1 that appears in the angular synchronization problem disappears from the spectrum of ${\mathcal{T}}_h$, a fact that may be attributed to the hairy ball theorem. The precise formula for the first four eigenvalues is

$$\begin{array}{cc}\hfill {\lambda }_1\left(h\right)& =\frac{1}{2}h-\frac{1}{8}{h}^2,\hfill \\ \hfill {\lambda }_2\left(h\right)& =\frac{1}{2}h-\frac{5}{8}{h}^2+\frac{1}{6}{h}^3,\hfill \\ \hfill {\lambda }_3\left(h\right)& =\frac{1}{2}h-\frac{11}{8}{h}^2+\frac{25}{24}{h}^3-\frac{15}{64}{h}^4,\hfill \\ \hfill {\lambda }_4\left(h\right)& =\frac{1}{2}h-\frac{19}{8}{h}^2+\frac{27}{8}{h}^3-\frac{119}{64}{h}^4+\frac{7}{20}{h}^5.\hfill \end{array}$$

These formulas are valid for all values of h ∈ [0, 2]. The graphs of λ_n(h), for n = 1, 2, 3, 4, are given in Figure 6.

Figure 6.

The eigenvalues λ_n(h) of the local parallel transport operator ${\mathcal{T}}_h$ for n = 1, 2, 3, 4.

The second result states that the eigenspace of multiplicity 3 (n = 1) corresponds to the largest eigenvalue of ${\mathcal{T}}_h$. That is, λ₁(h) > λ_n(h) for n ≥ 2 and for all h ∈ [0, 2]. For example, Figure 6 demonstrates that λ₁(h) dominates λ₂(h), λ₃(h), and λ₄(h). The spectral gap is evident from Figure 6, which shows that for small values of h the second largest eigenvalue among the first four eigenvalues is λ₂(h). In fact, λ₂(h) > λ_n(h) for all h ≤ 1/2 and n ≥ 3 (note that λ₂(h) has its maximum at h = 1/2). Hence, the spectral gap Δ(h) is

$$\Delta \left(h\right)={\lambda }_1\left(h\right)-{\lambda }_2\left(h\right)=\frac{5}{8}{h}^2-\frac{1}{8}{h}^2-\frac{1}{6}{h}^3~\frac{1}{2}{h}^2\text{for}h\ll 1.$$ (4.4)

The third result states that if R_i, R_j ∈ SO(3) are two rotations, and ψ₁, ψ₂, ψ₃ form an orthonormal basis for the top eigenspace of ${\mathcal{T}}_h$ of multiplicity 3, that is, ψ₁, ψ₂, ψ₃ are the top three eigenfunctions of ${\mathcal{T}}_h$ satisfying

$${\mathcal{T}}_h{\psi }_m={\lambda }_1\left(h\right){\psi }_m,m=1,2,3,$$

then

$$\langle \upsilon \left(R_i\right),\upsilon \left(R_j\right)\rangle =2\frac{\mid \langle \Psi \left(R_i\right),\Psi \left(R_j\right)\rangle \mid }{\Vert \Psi \left(R_i\right)\Vert \Vert \Psi \left(R_j\right)\Vert }-1,$$ (4.5)

where for every rotation R ∈ SO(3) we define the vector $\Psi \left(R\right)\in {\mathbb{C}}^3$ as

$$\Psi \left(R\right)=({\psi }_1\left(R\right),{\psi }_2\left(R\right),{\psi }_3\left(R\right)).$$ (4.6)

Note that the dot product on the left-hand side of (4.5) is between vectors in ${\mathbb{R}}^3$, while the dot product and norms on the right-hand side are of vectors in ${\mathbb{C}}^3$. The result (4.5) means that the top three eigenvectors of $\mathcal{H}$ allow us to express the dot product between the unknown viewing angles v(R_i) and v(R_j) in terms of the Hermitian dot product between their corresponding unit vectors $\frac{\Psi \left(R_i\right)}{\parallel \Psi \left(R_i\right)\parallel }$ and $\frac{\Psi \left(R_j\right)}{\parallel \Psi \left(R_j\right)\parallel }$ in ${\mathbb{C}}^3$. The third result is of extreme importance as it lies at the heart of our algorithm. In Appendix A we give an elementary proof of this result. That proof requires neither knowledge of representation theory nor familiarity with the tools developed in [12, 13].

5. Algorithm

Taking these three spectral properties into account leads to a simple algorithm for finding images that correspond to similar viewing angles. The input to the algorithm consists of n projection images P₁, …, P_n (n is often twice as large as the number of raw images, because for every raw image we artificially add its mirrored image). We now detail the various steps of the algorithm:

1. Compute the rotationally invariant distances⁷d_ij and the optimal alignment angles θ_ij as in (1.3) and (2.1) between all pairs of images.⁸

2. Construct the sparse n × n Hermitian matrix H as defined in (2.10), with the edge set E defined in (2.7) or, preferably, by taking the N nearest neighbors of every image (where N ≪ n is a fixed parameter).

3. Since some vertices may have more edges than others, we define $\tilde{H}$ = D⁻¹H, where D is an n × n diagonal matrix with $D_{ii}={\Sigma }_{j=1}^n\mid H_{ij}\mid$. Notice that $\tilde{H}$ is similar to the Hermitian matrix D^−½HD^−½.

4. Compute the top three normalized eigenvectors of $\tilde{H}$, denoted ${\psi }_1,{\psi }_2,{\psi }_3\in {\mathbb{C}}^n$. Since $\tilde{H}$ is a sparse matrix, its top three eigenvectors are most efficiently computed using an iterative method, such as the MATLAB eigs function.

5. Use ψ₁, ψ₂, ψ₃ to define n vectos ${\Psi }_1,\dots ,{\Psi }_n\in {\mathbb{C}}^3$ by

   $${\Psi }_i=({\psi }_1\left(i\right),{\psi }_2\left(i\right),{\psi }_3\left(i\right)),i=1,\dots ,n,$$ (5.1)

   where ψ_j(i) is the ith entry of the vector ψ_j (j =1,2,3).
6. Define a measure of affinity G_ij between images P_i and P_j as

   $$G_{ij}=2\frac{\mid \langle {\Psi }_i,{\Psi }_j\rangle \mid }{\Vert {\Psi }_i\Vert \Vert {\Psi }_j\Vert }-1,i,j=1,\dots ,n.$$ (5.2)
7. Declare neighbors of P_i as

   $$\text{neighbors of}{P}_i=\{j:G_{ij}>1-\gamma \},$$ (5.3)

   where 0 < γ ⪡ 1 controls the size of the neighborhood, or, alternatively, it is also possible to choose some fixed number of the largest G_ij values to define neighbors.

In section 6 we consider a specific model for which the algorithm is shown to successfully detect the true neighbors, while in section 7 we detail the results of numerous experiments that demonstrate its usefulness in practice. Moreover, in subsection 7.4 we describe a generalization of the algorithm that uses more than three eigenvectors and discuss the reason for which it succeeds even if the viewing directions are not uniformly distributed.

6. Probabilistic model and random matrix theory

We now explain why the algorithm succeeds in identifying the true neighbors. To that end, we will assume a specific probabilistic model for the entries of H. Our simplified model tries to capture and approximate the main features of the matrix H when it is constructed by computing rotationally invariant distances and optimal angles between noisy images.

We start by randomly generating n rotations R₁, …, R_n uniformly (according to the Haar measure) on SO(3). Our model assumes that if P_i and P_j are two projection images whose viewing angles both belong to a small spherical cap of size α, then with probability p the rotationally invariant distance d_ij will be small enough such that there would be an edge between them in the graph (i.e., {i, j} ∈ E) and that the optimal angle θ_ij would be accurate in the sense that it would be given by (2.5)–(2.6). With probability 1 − p the distance d_ij is not small enough for creating an edge between i and j, and instead there would be a link between i to some random vertex, drawn uniformly at random from the remaining vertices (not already connected to i). We assume that if the link between i and j is a random link (such that the corresponding viewing angles are far away from each other), then the optimal in-plane rotation angle θ_ij is uniformly distributed in [0, 2π). In our model, the only links existing between projection images P_i and P_j whose viewing angles do not belong to a small spherical cap of size α are these shortcut edges obtained by rewiring other good links, and there are no other links between them. In other words, our model assumes that the underlying graph of links between noisy images is a small-world graph on the sphere, with edges being randomly rewired with probability 1 − p. The angles take their correct values for true links and random values for shortcut edges.

The matrix H is a random matrix under this model. Since the expected value of the random variable e^ıθ vanishes for θ ~ Uniform[0,2π), that is, $\mathbb{E}{e}^{ı\theta }=0$, we have that the expected value of the matrix H is

$$\mathbb{E}H=p{H}^{clean},$$ (6.1)

where H^clean is the class averaging matrix that corresponds to p = 1 obtained in the case that all links and angles are inferred correctly. Here we take full advantage of our construction of H that sets the elements of H to be complex-valued numbers that average to 0 (instead of nonnegative entries like 0 and 1 of the adjacency matrix that cannot have zero mean). We conclude that the matrix H can be decomposed as

$$H=p{H}^{clean}+R,$$ (6.2)

where R is a random matrix whose elements are independent and identically distributed (i.i.d.) zero mean random variables with finite moments (the elements of R are all bounded). The decomposition (6.2) is extremely useful, as it means that the top eigenvectors of H approximate the top eigenvectors of H^clean as long as the 2-norm of R is not too large. Bounds on the spectral norm of random sparse matrices are proved in [16, 15]. Adapting [16, Theorem 2.1, p. 126] to our case shows that ${\Vert R\Vert }_2=O\left(\alpha \sqrt{n}\right)$ with high probability, since the average degree of the graph is $n{\text{sin}}^2\frac{\alpha }{2}=O\left({\alpha }^{2}n\right)$. In the next section we provide the results of numerical experiments from which it seems that the distribution of the eigenvalues of R follows Wigner's semicircle law [30, 31]. Moreover, we note that the spectral norm of H^clean is O(nα²), since $\frac{1}{n}{H}^{clean}$ converges to the operator $\mathcal{H}$ (given in (4.2)) whose spectral norm is O(h) = O(α²). Similarly, the spectral gap of H^clean is O(nh²) = O(nα⁴), since the spectral gap of $\mathcal{H}$ is O(h²) = O(α⁴) (see (4.4)). The decomposition (6.2) and the bound on ‖R‖₂ imply that the top three eigenvectors of H approximate the top three eigenvectors of H^clean as long as ‖R‖₂ is smaller than the spectral gap of pH^clean or, equivalently, for p > p_c, where $p_c=p_c(\alpha ,n)=O\left(\frac{1}{{\alpha }^3\sqrt{n}}\right)$ is the threshold probability that depends on the size of the cap and the number of images.

As discussed earlier, the matrix $\frac{1}{n}{H}^{clean}$ converges almost surely to the operator $\mathcal{H}$ in the limit n → ∞. This convergence rate is at least as fast as $\frac{1}{\sqrt{n}}$ due to the law of large numbers. Altogether, it follows that for large enough n, the linear span of the top three eigenvectors of H is a discrete approximate of the top eigenspace of $\mathcal{H}$, because the top eigenvectors of H approximate the top eigenvectors of H^clean, but these approximate the top eigenfunctions of $\mathcal{H}$. Finally, the spectral properties of $\mathcal{H}$ (section 4) ensure the success of the algorithm under this probabilistic model.

7. Numerical experiments

We conducted two types of numerical experiments. The first type involves simulations of the probabilistic model of section 6. The second type mimics the experimental setup by applying the algorithm to noisy simulated projection images of a given 3D volume. We point out that there is no direct way to compare the performance of classification algorithms on real microscope images, since their viewing angles are unknown. The only way to compare classification algorithms on real data is indirectly, by evaluating the resulting 3D reconstructions. Here we conduct only numerical experiments from which conclusions can be drawn directly.

All experiments in this section were executed on a Linux machine with eight Xeon 2.93GHz cores and 48GB of RAM. Unless otherwise specified, the executed code was not parallelized and so only one core was active.

7.1. Experiments with the probabilistic model

The purpose of the first experiment of this type is to illustrate the emergence of Wigner's semicircle law and the performance of the algorithm for n = 1000, cos α = 0.7 (α = 45.6°, and different values of p. We chose this relatively small value for n (n = 1000), because showing the semicircle requires the computation of all eigenvalues of H, not just the few top ones that are required by the algorithm. Also, the value of α = 45.6° is too large to be considered realistic, as it implies that projection images whose viewing angles differ by as much as 45° are similar enough to have a small rotationally invariant distance. We chose this high value of α so that the underlying graph would have enough edges and the spectral gap would be noticeable. The number of graph edges in this experiment is m ≈ 37,500. We emphasize once again that the purpose of this experiment is of an illustrational nature.

Figure 7 summarizes the results of the first experiment. Evident from the histogram of the eigenvalues of H (left column) is the emergence of the semicircle that gets slightly wider as p decreases (the right edges of the semicircles never exceed 25). The multiplicities 3, 5, 7, … of the top eigenvalues are clearly demonstrated in the bar plots of the eigenvalues (middle column). The top three eigenvalues of H are separated from the semicircle as long as p is not too small. Note that the decrease of these three eigenvalues as p is decreased stands in full agreement with (6.2), which shows that they scale linearly with p as they correspond to the eigenvectors of H^clean. The right column shows scatter plots of the G_ij values that were estimated from the algorithm (y-axis) against the dot products 〈v_i, v_j〉 of the simulated (true) rotations R₁, …, R_n with v_i = R_i³, i = 1, …, n. Figure 7(c) shows that the dot products between the normalized unit vectors in ${\mathbb{C}}^3$ that are computed from the top three eigenvectors of H are equal (up to numerical errors) to the dot products of the corresponding viewing angles. In particular, large G_ij values imply large 〈v_i, v_j〉 values; that is, they indicate the correct neighbors. The scattered points get more spread as the value for p decreases. The numerical results show that the spreading is wider for large distances (small values of the dot product, bottom-left corner) and is narrower for small distances. This narrowing near the top-right corner is very appealing, because it allows us to better distinguish the true neighbors.

Figure 7.

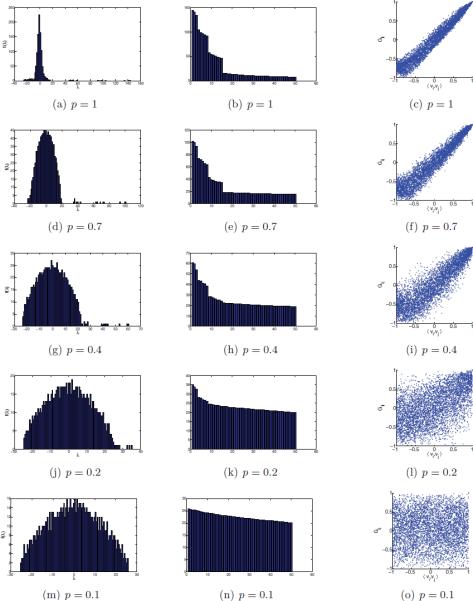
n = 1000, α = 45.6° , and different values of p . Left column: histogram of the eigenvalues of H . Middle column: bar plot of the top 50 eigenvalues of H . Right column: scatter plot of G_ij as estimated in step 6 of the algorithm (y-axis) against the dot product of the true simulated viewing angles 〈v_i, v_j〉 (x-axis).

In the second experiment, we used parameter values that are more realistic: n = 40,000, cos α = 0.95 (α = 18.2°), and different values of p. The number of edges was m ≈ 10⁷. The running time for each value of p was about 2 minutes, which includes the construction of the graph and the computation of the top 20 eigenvalues of H using the MATLAB eigs function. Note that this running time is negligible compared to the time required to compute all n(n − 1)/2 rotationally invariant distances. The results of this experiment are summarized in Figure 8. The spectral gap between the top three eigenvalues of H and the remaining spectrum, though small, is noticeable even for p = 0.1 (90% false links), and even the multiplicities 5 and 7 are easily distinguishable (see Figure 8(d)). The estimated G_ij's provide a very good approximation to the dot products 〈v_i, v_j〉 between the true viewing angles, and the approximation is especially good for neighboring pairs, even for p = 0.2 (80% of shortcut edges), as can be seen in Figure 8(h). Even for p = 0.1 (Figure 8(i)), the identification of the neighbors based on the large G_ij values is quite good, and there are only a few images that the algorithm would confusingly consider as neighbors.

Figure 8.

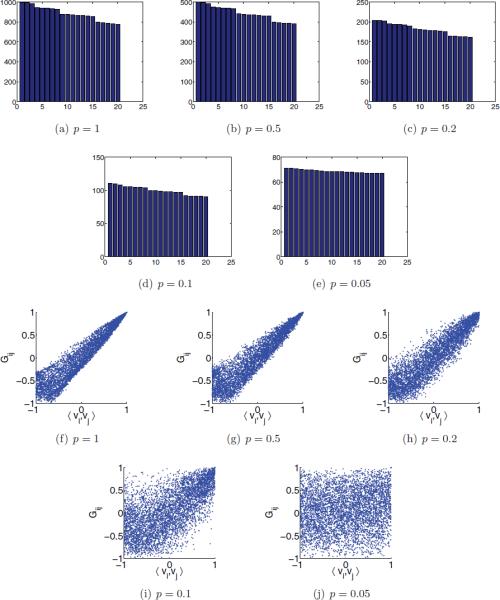
n =40000, α = 18.2° , and different values of p . Top two rows: bar plot of the top 20 eigenvalues of H . Bottom two rows: scatter plot of G_ij as estimated in step 6 of the algorithm (y-axis) against the dot product of the true simulated viewing angles 〈v_i , v_j〉 (x-axis).

7.2. Experiments with noisy simulated images

In the second series of experiments, we tested the eigenvector method on different sets of 20,000 simulated noisy projection images of the ribosomal 50S subunit, each set corresponding to a different level of noise. Including the mirrored images, the total number of images was n = 40,000. The simulated images were generated as noise-free centered projections of the macromolecule, whose corresponding rotations were uniformly distributed SO(3). Each projection was of size 129 × 129 pixels. Next, we fixed a signal-to-noise ratio (SNR), and added to each clean projection additive Gaussian white noise of the prescribed SNR. The SNR in all our experiments is defined by

$$\text{SNR}=\frac{\text{Var}\left(Signal\right)}{\text{Var}\left(Noise\right)},$$ (7.1)

where Var is the variance (energy), Signal is the clean projection image, and Noise is the noise realization of that image. Figure 9 shows one of the projections at different SNR levels.

Figure 9.

Simulated projection with various levels of additive Gaussian white noise.

For each set of n = 40,000 simulated images with a fixed SNR, we need to compute all $\left(\begin{array}{c}\hfill n\hfill \\ \hfill 2\hfill \end{array}\right)$ rotationally invariant distances (1.3) and optimal alignment angles (2.1). This computation can be quite time consuming. Also, we need to pay special attention to making the computation accurate, as it involves rotating images that are specified on a Cartesian grid rather than on a polar grid. There are quite a few papers that deal with the problem of fast and accurate rotational alignment of images; see, e.g., [22, 14, 6]. In the experiments reported here we rotationally align the images using a method that we recently developed that uses a steerable basis of eigenimages [21, 32]. Using this method, we computed the $\left(\begin{array}{c}\hfill 40,000\hfill \\ \hfill 2\hfill \end{array}\right)$ rotational alignments in about 30 minutes using all eight cores (here the computation ran in parallel). The images are first radially masked since pixels near the image boundaries (also known as the “ears”) correspond to noise rather than signal. Then, the masked images are linearly projected onto the subspace spanned by a specified number M of eigenimages that correspond to the largest eigenvalues of the images' covariance matrix. After this linear projection, the images are represented by their M expansion coefficients instead of their original pixelwise representation, thus achieving significant compression for M ≪ 129². This compression not only facilitates a faster computation for rotational alignment but also amounts to filtering. The particular choice of M can be assisted by inspecting the numerical spectrum of the covariance matrix, but we do not go into the details of this procedure. For SNR = 1/64 we used M = 55 eigenimages, for SNR = 1/32 we used M = 90, for SNR = 1/16 we used M = 120, and for higher values of the SNR we used M = 200.

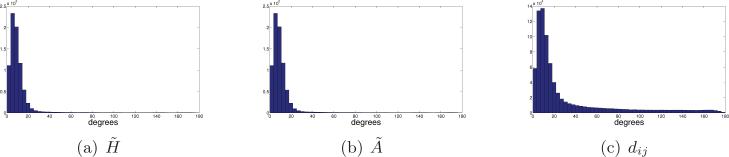
The histograms of Figure 10 demonstrate the ability of small rotationally invariant distances to indicate images with similar viewing directions. For each image we use the rotationally invariant distances to find its 40 nearest neighbors among the entire set of 40,000 images. In our simulation we know the original viewing directions, so for each image we compute the angles (in degrees) between the viewing direction of the image and the viewing directions of its 40 neighbors. Small angles indicate successful identification of “true” neighbors that belong to a small spherical cap, while large angles correspond to outliers, that later lead to shortcut edges in the graph. We see that for SNR = 1/2 there are no outliers, and all the viewing directions of the neighbors belong to a spherical cap whose opening angle is about 8°. However, for lower values of the SNR, there are outliers, indicated by arbitrarily large angles (all the way to 180°).

Figure 10.

Histograms of the angle (in degrees, x-axis) between the viewing directions of 40,000 images and the viewing directions of their 40 nearest neighboring images as found by computing the rotationally invariant distances.

After computing the rotationally invariant distances and optimal alignment angles, we use the N = 40 nearest neighbors of each image to construct the sparse matrix H using the “intersection” rule (i.e., {i, j} ∈ E iff i is one of the 40 nearest neighbors of j and j is one of the 40 nearest neighbors of i). Note that, following the application of the intersection rule, it may happen (especially for low values of the SNR) that some vertices are of degree 0 (i.e., vertices that have no links with other vertices). We delete from the matrix H the rows and columns corresponding to degree 0 vertices. After this removal, it is still possible for different vertices to have different degrees (between 1 and 40), rendering the importance of the normalization step $\tilde{H}=D^{-1}H$. We then compute the eigenvectors and eigenvalues of $\tilde{H}$. Figure 11 shows the top 10 eigenvalues of $\tilde{H}$ for different values of the SNR. The multiplicity 3, and even the multiplicity 5, are evident for high values of the SNR, such as SNR = 1/2 and SNR = 1/16. Figure 12 shows scatter plots of the dot products between the viewing directions 〈v_i, v_j〉 and the G_ij's that are deduced from the computed eigenvectors. For SNR = 1/2, SNR = 1/16, and SNR = 1/32 we get the desired linear correspondence between 〈v_i, v_j〉 and G_ij from which we can infer the true neighbors. For SNR = 1/64 we do not get the desired spectrum, and from the values of G_ij we cannot infer the true neighbors. Still, a closer examination of the scatter plot for SNR = 1/64 reveals that points are not scattered randomly but rather have some structure. In section 7.4 we discuss how to improve the identification of true neighbors, but already at this point we have established that our method works well even for SNR as low as 1/32.

Figure 11.

Bar plots of the 10 largest eigenvalues ${\left\{{\lambda }_i\right\}}_{i=1}^{10}$ of $\tilde{H}$. Since the eigenvalues are very close to 1, the y-axis corresponds to 1 − λ.

Figure 12.

Scatter plots of G_ij (computed from the top three eigenvectors of $\tilde{H}$) against 〈v_i, v_j〉.

7.3. Numerical comparison with diffusion maps

We compared our algorithm against what we refer to as the “diffusion maps” approach. Diffusion maps were introduced in [3], but here we do not assume the reader to be familiar with that method in its generality. We are not aware of any earlier attempts to apply diffusion maps for the solution of the class averaging problem in cryo-EM. We note, however, that the diffusion maps approach presented below is quite similar to our solution to the problem of two-dimensional (2D) random tomography [5], where the goal is to find the unknown viewing angles of one-dimensional (1D) tomographic projections of an unknown 2D object; see also [1, 2]. In that regard, we emphasize that the main difference between the 3D cryo-EM class averaging problem and its 2D counterpart is perhaps the extra angular information that we encode in the class averaging matrix H. This angular information does not exist in the 2D problem, where 1D projection signals (instead of 2D images) are compared.

In the diffusion maps approach, the matrix H is replaced by the adjacency matrix A of the graph G = (V, E). Specifically,

$$A_{ij}=\{\begin{array}{c}1,\{i,j\}\in E,\hfill \\ 0,\{i,j\}\notin E.\hfill \end{array}\phantom{\}}$$ (7.2)

Notice that A_ij = |H_ij|. We normalize the matrix A the same way we normalized H. That is, we define $\tilde{A}$ as $\tilde{A}=D^{-1}A$. Under the “clean” model of section 6, the eigenvectors of A approximate the eigenfunctions of an integral operator over the sphere whose kernel function is the characteristic function of a small spherical cap. As such, this operator commutes with rotations, and from the Funk-Hecke theorem [19, p. 195] it follows that its eigenfunctions are the spherical harmonics, whose multiplicities are 1, 3, 5,… (see, e.g., the discussion in [4, section 4.4]). In particular, the second, third, and fourth eigenvectors φ₂, φ₃, and φ₄ of $\tilde{A}$ correspond to the linear spherical harmonics x, y, and z (multiplicity 3), where v = (x, y, z) is the viewing direction. The first eigenvector φ₁ corresponds to the constant function and is therefore not required by this method. This motivates us to define

$${\Phi }_i=({\varphi }_2\left(i\right),{\varphi }_3\left(i\right),{\varphi }_4\left(i\right))$$

and

$$G_{ij}^{\prime }=\frac{\langle {\Phi }_i,{\Phi }_j\rangle }{\Vert {\Phi }_i\Vert \Vert {\Phi }_j\Vert }.$$

The above discussion implies that under the “clean” model of section 6 we have that $G_{ij}^{\prime }=\langle v_i,v_j\rangle$.

Figure 13 depicts bar plots of the largest 10 eigenvalues of the matrix $\tilde{A}$ for different values of the SNR. Notice that λ₁ = 1 and that the multiplicity 3 of λ₂, λ₃, λ₄ and the multiplicity 5 of λ₅,…, λ₉ are evident for SNR = 1/2 and SNR = 1/16. Figure 14 shows scatter plots of $G_{ij}^{\prime }$ against 〈v_i, v_j〉. The diffusion maps approach works well even for SNR = 1/32, but also breaks down for SNR = 1/64.

Figure 13.

Bar plots of the 10 largest eigenvalues ${\left\{{\lambda }_i\right\}}_{i=1}^{10}$ of $\tilde{H}$. Since the eigenvalues are very close to 1 , the y-axis corresponds to 1 − λ.

Figure 14.

Scatter plots of $G_{ij}^{\prime }$ (computed from the second, third, and fourth eigenvectors of $\tilde{A}$) against 〈v_i, v_j〉.

From the numerical experiments shown thus far we cannot conclude that the eigenvectors of $\tilde{H}$ outperform the eigenvectors of $\tilde{A}$ in terms of improving the identification of the true neighbors. We therefore conducted another experiment with SNR = 1/40. From Figure 15 we draw the conclusion that the method based on the matrix $\tilde{H}$ outperforms the diffusion maps approach.

Figure 15.

SNR = 1/40: scatter plots using the eigenvectors of $\tilde{H}$ (left) and using the eigenvectors of $\tilde{A}$(right).

7.4. Using more than three eigenvectors

Thus far we have seen the usefulness of the H matrix method for SNRs as low as 1/40, but it was not successful for SNR = 1/64. Also, the reader may question the validity of the assumption that the viewing directions are uniformly distributed over the sphere, an assumption that seems essential in order to get the linear relation between G_ij and 〈v_i, v_j〉. We now address these important issues using both theory and numerical simulations.

The first point that we would like to make here is that in the class averaging problem, we are not required to find the viewing directions of the images. We just need to find images with similar viewing directions. Once the neighboring images are identified, they can be rotationally aligned and averaged to produce images of higher SNR, and later procedures that are based on common lines and refinements can be used to deduce the viewing directions of the class averages. Asking for the viewing directions is perhaps too much to require at this preliminary stage of the data processing. Instead, we can settle for improving our identification of neighbors.

The second point that we raise is that the eigenvectors of the matrix $\tilde{H}$ approximate the eigenfunctions of an integral operator over SO(3), even if the viewing directions are not uniformly distributed. Since the eigenfunctions are continuous (they become more oscillatory for smaller eigenvalues of $\tilde{H}$), it follows that the eigenvectors of $\tilde{H}$ do not change by much (as tangent vector fields to the sphere) for images whose viewing directions are restricted to the same spherical cap. However, we do not need to restrict ourselves to just the top three eigenvectors as we have done up to this point. We can use more than just three eigenvectors in order to identify images with similar viewing directions. Let K ≥ 3 be the of eigenvectors ψ₁, ψ₂,…, ψ_K that we use. For the ith image (i = 1, …, n) we define ${\Psi }_i^K\in {\mathbb{C}}^K$ as

$${\Psi }_i^K=({\psi }_1\left(i\right),{\psi }_2\left(i\right),\dots ,{\psi }_K\left(i\right)).$$ (7.3)

Moreover, we define the similarity measure $G_{ij}^K$ between image i and image j as

$$G_{ij}^K=\frac{\mid \langle {\Psi }_i^K,{\Psi }_j^K\rangle \mid }{\Vert {\Psi }_i^K\Vert \Vert {\Psi }_i^K\Vert },$$ (7.4)

and we postidentify an image j as a neighbor of image i if $G_{ij}^K$ is large enough.

This classification method is proved to be quite powerful in practice. We applied it with K = 80 to the set of noisy images with SNR = 1/64, for which we observed already that K = 3 failed. For every image we find its 40 nearest neighbors based on $G_{ij}^K$. In the simulation we know the viewing directions of the images, and we compute for each pair of suspected neighboring images the angle (in degrees) between their viewing directions. The histogram of these angles is shown in Figure 16(a). About 92% of the identified images belong to a small spherical cap of opening angle 20°, whereas this percentage is only about 65% when neighbors are identified by the rotationally invariant distances (Figure 16(c)). For the diffusion maps approach, it is also possible to use K≥ 3 eigenvectors. The result of the diffusion maps approach with K = 80 is shown in Figure 16(b). Also for this modified diffusion maps approach about 92% of the identified images are in a spherical cap of opening angle 20°. We remark that for SNR = 1/50 this percentage goes up to about 98%. We did not experiment with SNRs below 1/64.

Figure 16.

SNR = 1/64. Histogram of the angles (x-axis, in degrees) between the viewing directions of each image (out of 40,000) and its 40 neighboring images. (a) Neighbors are postidentified usingK = 80 eigenvectors of $\tilde{H}$. (b) Neighbors are postidentified using 80 eigenvectors of $\tilde{A}$. (c) Neighbors are identified using the original rotationally invariant distances.

8. Summary and discussion

In this paper we introduced a new algorithm for identifying cryo-EM noisy projection images with nearby viewing angles. This identification is an important first step in 3D structure determination of macromolecules from cryo-EM, because once identified, these images can be rotationally aligned and averaged to produce “class averages” of better quality. The main advantage of our algorithm is its extreme robustness to noise. The algorithm is also very effcient in terms of running time and memory requirements, as it is based on the computation of the top few eigenvectors of a sparse Hermitian matrix. These advantages were demonstrated in our numerical experiments.

The main core of our algorithm is a special construction of a sparse Hermitian matrix H. The nonzero entries of H correspond to pairs of images whose rotationally invariant distances are relatively small. The nonzero entries are set to take complex-valued numbers of unit magnitude, with phases that are equal to the optimal in-plane rotational alignment angles between the images. We show that images with nearby viewing angles are identified from the top three eigenvectors of that matrix. The construction of the matrix H here is similar to the construction in our solution to the angular synchronization problem [23]. The main difference is that while angular synchronization required only the top eigenvector, here we need the top three eigenvectors in order to identify images with nearby viewing directions. We explain this difference using the topology of the sphere and, more specifically, the hairy ball theorem.

The robustness of the algorithm is guaranteed by random matrix theory, whose application here is made possible by the special construction of H, since the average of points on the unit circle in the complex plane is 0. The admissibility (correctness) of the algorithm follows from the spectral properties of H, which result from the fact that H is a discretization of a local version of the parallel transport operator on S². The exact analysis of the spectral properties of this local parallel transport operator are reported in [13] using representation theory.

The assumption that the viewing angles are uniformly distributed over S² is important to our spectral analysis, though it may not hold for some experimental data sets. We emphasize that our algorithm identifies the correct neighbors also for nonuniform distributions, because the eigenvectors of H (and $\tilde{H}$) are continuous as a function of the viewing directions, regardless of the underlying distribution. In other words, a large value for G_ij indicates that P_i and P_j have similar viewing angles also in the case of a nonuniform distribution. We also showed numerical results in which using more than three eigenvectors improves the identification of the true neighbors.

Throughout this paper we assumed the homogeneity case, that is, that all images correspond to the exact same 3D structure of the molecule. In the heterogeneity case, the molecule may have several different conformations, so that projection images also need to be classified accordingly. This classification is often extremely difficult, due to the low SNR of the images and the similarity between the 3D structures of the different conformations. We believe that the algorithm presented here may assist in solving the conformational classification problem.

We are currently applying our algorithms to real microscope image data sets. Handling real microscope images requires paying special attention to issues such as the contrast transfer function of the microscope that may be changing from one image to another, translational alignment, and other practical issues that are beyond the scope of this paper. Finally, the ideas presented here can be used in other applications that require a global rotational alignment of images, such as the structure-from-motion problem in computer vision.

Appendix A. Parallel transport on the sphere and related operators

Our algorithm is heavily based on (4.5), which provides a way to express the dot product between unknown viewing angles using the Hermitian dot product between vectors in ${\mathbb{C}}^3$ obtained from an orthonormal basis of the maximal eigenspace of multiplicity 3 of the local parallel transport operator ${\mathcal{T}}_h$. In this appendix we calculate an explicit orthonormal basis for this eigenspace and give an elementary verification of identity (4.5) without using representation theory. In passing, we make a few important observations about the parallel transport operator that go beyond the mere purpose of identifying its maximal eigenspace. In particular, we relate the parallel transport operator to two other integral operators, which we call the common lines operator and the orthographic lines operator, first introduced in [24] and [12], respectively, as well as their localized versions. At first we disregard the complex structure, thinking of ${\mathcal{T}}_{R_i,R_j}$ as a map from ${\mathbb{R}}^2$ to ${\mathbb{R}}^2$.

A.1. Common lines and orthographic lines

One of the fundamental concepts in cryo-EM is that of the common line [26, 27]: if P_i and P_j are two projection images with corresponding rotations R_i and R_j, then the two planes v(R_i)^⊥ and v(R_j)^⊥ must have a common line of intersection whose normalized direction in ${\mathbb{R}}^3$ is the unit vector

$$\frac{\upsilon \left(R_i\right)\times \upsilon \left(R_j\right)}{\Vert \upsilon \left(R_i\right)\times \upsilon \left(R_j\right)\Vert }=\frac{R_i^3\times R_j^3}{\Vert R_i^3\times R_j^3\Vert }.$$ (A.1)

Using the orthonormal bases $R_i^1$, $R_i^2$ for v(R_i)⊥ and $R_j^1$, $R_j^2$ for v(R_i)⊥, the unit vector (A.1) is identified with the unit vectors (A.1) is identified with the unit vectors $c_{ij}\in T_{R_i}={\mathbb{R}}^2$ and $c_{ji}\in T_{R_j}={\mathbb{R}}^2$, given by

$$c_{ij}=\left(\begin{array}{ccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \end{array}\right)R_i^{-1}\frac{R_i^3\times R_j^3}{\Vert R_j^3\times R_j^3\Vert }$$ (A.2)

and

$$c_{ji}=\left(\begin{array}{ccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \end{array}\right)R_j^{-1}\frac{R_i^3\times R_j^3}{\Vert R_i^3\times R_j^3\Vert }.$$ (A.3)

Note that the cross product satisfies

$$\left(R{w}_1\right)\times \left(R{w}_2\right)=R(w_1\times w_2)\text{for all}R\in SO\left(3\right)\text{and}{w}_1,w_2\in {\mathbb{R}}^3.$$

The common lines (A.2)–(A.3) can therefore be simplified using

$$R_i^{-1}(R_i^3\times R_j^3)=\left(R_i^{-1}{R}_i^3\right)\times \left(R_i^{-1}{R}_j^3\right)=I^3\times U^3=\left(\begin{array}{c}\hfill -U_{23}\hfill \\ \hfill U_{13}\hfill \\ \hfill 0\hfill \end{array}\right)$$ (A.4)

and

$$R_j^{-1}(R_i^3\times R_j^3)=\left(R_j^{-1}{R}_i^3\right)\times \left(R_j^{-1}{R}_j^3\right)={\left(U^{-1}\right)}^3\times I^3=\left(\begin{array}{c}\hfill U_{32}\hfill \\ \hfill -U_{31}\hfill \\ \hfill 0\hfill \end{array}\right),$$ (A.5)

where $U=R_i^{-1}{R}_j$, U³ is its third column, and I³ = (0 0 1)^T is the third column of the 3 × 3 identity matrix I. As rotations are isometries, we also have that

$${\Vert R_i^3\times R_j^3\Vert }^2={\Vert R_i(I^3\times U^3)\Vert }^2={\Vert I^3\times U^3\Vert }^2={\left(U_{13}\right)}^2+{\left(U_{23}\right)}^2=1-{\left(U_{33}\right)}^2.$$ (A.6)

It follows from (A.4)–(A.6) that the common lines (A.2)–(A.3) are given by

$$c_{ij}=\frac{1}{\sqrt{1-{\left(U_{33}\right)}^2}}\left(\begin{array}{c}\hfill -U_{23}\hfill \\ \hfill U_{13}\hfill \end{array}\right)$$ (A.7)

and

$$c_{ji}=\frac{1}{\sqrt{1-{\left(U_{33}\right)}^2}}\left(\begin{array}{c}\hfill U_{32}\hfill \\ \hfill -U_{31}\hfill \end{array}\right).$$ (A.8)

We proceed to define the orthographic lines o_ij and o_ji. Let ${\tilde{o}}_{ij}\in {\mathbb{R}}^3$ be the normalized projection of v(R_j) onto v(R_i)^⊥, given by

$${\tilde{o}}_{ij}=\frac{\langle R_i^1,R_j^3\rangle R_i^1+\langle R_i^2,R_j^3\rangle R_i^2}{\sqrt{1-{\langle R_i^3,R_j^3\rangle }^2}},$$ (A.9)

and let ${\tilde{o}}_{ji}\in {\mathbb{R}}^3$ be the normalized projection of v(R_i) onto v(R_j)⊥, given by

$${\tilde{o}}_{ji}=\frac{\langle R_j^1,R_i^3\rangle R_j^1+\langle R_j^2,R_i^3\rangle R_j^2}{\sqrt{1-{\langle R_i^3,R_j^3\rangle }^2}}.$$ (A.10)

We identify ${\tilde{o}}_{ij}$ and ${\tilde{o}}_{ji}$ with the vectors o_ij ∈ T_Ri and o_ji ∈ T_Rj, respectively, written explicitly as

$$o_{ij}=\frac{1}{\sqrt{1-{\langle R_j^3,R_i^3\rangle }^2}}\left(\begin{array}{c}\hfill \langle R_i^1,R_j^3\rangle \hfill \\ \hfill \langle R_i^2,R_j^3\rangle \hfill \end{array}\right)=\frac{1}{\sqrt{1-{\left(U_{33}\right)}^2}}\left(\begin{array}{c}\hfill U_{13}\hfill \\ \hfill U_{23}\hfill \end{array}\right)$$ (A.11)

and

$$o_{ji}=\frac{1}{\sqrt{1-{\langle R_j^3,R_i^3\rangle }^2}}\left(\begin{array}{c}\hfill \langle R_j^1,R_i^3\rangle \hfill \\ \hfill \langle R_j^2,R_i^3\rangle \hfill \end{array}\right)=\frac{1}{\sqrt{1-{\left(U_{33}\right)}^2}}\left(\begin{array}{c}\hfill U_{31}\hfill \\ \hfill U_{32}\hfill \end{array}\right).$$ (A.12)

The common lines (A.7)–(A.8) and the orthographic lines (A.11)–(A.12) are related through

$$c_{ij}=J{o}_{ij},c_{ji}=-J{o}_{ji},$$ (A.13)

where

$$J=\left(\begin{array}{cc}\hfill 0\hfill & \hfill -1\hfill \\ \hfill 1\hfill & \hfill 0\hfill \end{array}\right)$$ (A.14)

is the 2 × 2 rotation matrix by 90°. Note that J^T = J⁻¹ = −J and that multiplication by J is equivalent to multiplication by ı in the complex structure. From (A.13) it follows that the orthographic lines are perpendicular to the common lines, that is, $c_{ij}^T{o}_{ij}=c_{ji}^T{o}_{ji}=0$, because χ^TJχ = 0 for every $x\in {\mathbb{R}}^2$.

A.2. Common lines kernel, orthographic lines kernel, and parallel transport kernel

We define the orthographic lines kernel as the 2 × 2 rank-one matrix ${\mathcal{O}}_{R_i,R_j}$ that maps the orthographic line o_ji to the orthographic line o_ij:

$${\mathcal{O}}_{R_i,R_j}=o_{ij}{o}_{ji}^T=\frac{1}{1-{\left(U_{33}\right)}^2}\left(\begin{array}{c}\hfill U_{13}\hfill \\ \hfill U_{23}\hfill \end{array}\right)\left(U_{31}{U}_{32}\right).$$ (A.15)

Similarly, we define the common lines kernel as the 2 × 2 rank-one matrix ${\mathcal{C}}_{R_i,R_j}$ that maps the common line c_ji to the common line c_ij:

$$\begin{array}{cc}\hfill {\mathcal{C}}_{R_i,R_j}& =c_{ij}{c}_{ji}^T=J{o}_{ij}{(-J{o}_{ji})}^T=-J{\mathcal{O}}_{R_i,R_j}{J}^{-1}\hfill \\ \hfill & =\frac{1}{1-{\left(U_{33}\right)}^2}\left(\begin{array}{c}\hfill -U_{23}\hfill \\ \hfill U_{13}\hfill \end{array}\right)(U_{32}-U_{31}).\hfill \end{array}$$ (A.16)

Note that unlike the parallel transport kernel ${\mathcal{T}}_{R_i,R_j}$, the orthographic lines kernel ${\mathcal{O}}_{R_i,R_j}$ and the common lines kernel ${\mathcal{C}}_{R_i,R_j}$ do not respect the complex structure: they can be considered as maps from ${\mathbb{R}}^2$ to ${\mathbb{R}}^2$, but not as maps from $\mathbb{C}$ to $\mathbb{C}$.

Lemma A.1. The parallel transport kernel ${\mathcal{T}}_{R_i,R_j}$ admits the decomposition

$${\mathcal{T}}_{R_i,R_j}={\mathcal{C}}_{R_i,R_j}-{\mathcal{O}}_{R_i,R_j}.$$ (A.17)

Proof. The geometric definition of theorthographic line implies that ${\tilde{o}}_{ij}$ is the normalized velocity vector of the geodesic path from v(R_j) to v(R_i) at v(R_j). Similarly, the orthographic line ${\tilde{o}}_{ij}$ is the normalized velocity vector of the geodesic path from v(R_i) to v(R_j) at v(R_j). The differential geometric definition of parallel transport means that ${\mathcal{T}}_{R_i,R_j}$ maps o_ji to −o_ij. Moreover, since ${\mathcal{T}}_{R_i,R_j}$ is a rotation, it must also map Jo_ji to −Jo_ij. Therefore, in order to verify that ${\mathcal{T}}_{R_i,R_j}$ is indeed given by (A.17), we need to check that it satisfies

$${\mathcal{T}}_{R_i,{{R_j}^O}_{ji}}=-o_{ij}$$ (A.18)

and

$${\mathcal{T}}_{R_i,R_j}J{o}_{ji}=-J{o}_{ij},$$ (A.19)

but these follow immediately from (A.15), (A.16), and the orthogonality of the common lines and the orthographic lines:

$$\begin{array}{cc}\hfill ({\mathcal{C}}_{R_i,R_j}-{\mathcal{O}}_{R_i,R_j})o_{ji}& =(c_{ij}{c}_{ji}^T-o_{ij}{o}_{ji}^T)o_{ji}=-o_{ij},\hfill \\ \hfill ({\mathcal{C}}_{R_i,R_j}-{\mathcal{O}}_{R_i,R_j})J{o}_{ji}& =(-J{o}_{ij}{o}_{ji}^T{J}^{-1}-o_{ij}{o}_{ji}^T)J{o}_{ji}=-J{o}_{ij}.\hfill \end{array}$$

A.3. Global and local integral operators

Using the kernels ${\mathcal{C}}_{R_i,R_j}$, ${\mathcal{O}}_{R_i,R_j}$, and ${\mathcal{T}}_{R_i,R_j}$ we define the integral operators $\mathcal{C}$, $\mathcal{O}$, and $\mathcal{T}$ as follows:

$$\left(\mathcal{C}f\right)\left(R_i\right)={\int }_{SO\left(3\right)}{\mathcal{C}}_{R_i,R_j}f\left(R_j\right)d{R}_j,$$

$$\left(\mathcal{O}f\right)\left(R_i\right)={\int }_{SO\left(3\right)}{\mathcal{O}}_{R_i,R_j}f\left(R_j\right)d{R}_j,$$

$$\left(\mathcal{T}f\right)\left(R_i\right)={\int }_{SO\left(3\right)}{\mathcal{T}}_{R_i,R_j}f\left(R_j\right)d{R}_j,$$

where f is a function from SO(3) to ${\mathbb{R}}^2$. We refer to $\mathcal{C}$, $\mathcal{O}$, $\mathcal{T}$ and as the global common lines operator, the global orthographic lines operator, and the global parallel transport operator, respectively.

We also define the local integral operator ${\mathcal{C}}_h$, ${\mathcal{O}}_h$, and ${\mathcal{T}}_h$,for h∈[0,2], as

$$\left({\mathcal{C}}_{h}f\right)\left(R_i\right)={\int }_{R_j\in SO\left(3\right):\langle v\left(R_i\right),v\left(R_j\right)\rangle >1-h}{\mathcal{C}}_{R_i,R_j}f\left(R_j\right)d{R}_j,$$ (A.20)

$$\left({\mathcal{O}}_{h}f\right)\left(R_i\right)={\int }_{R_j\in SO\left(3\right):\langle v\left(R_i\right),v\left(R_j\right)\rangle >1-h}{\mathcal{O}}_{R_i,R_j}f\left(R_j\right)d{R}_j,$$ (A.21)

$$\left({\mathcal{T}}_{h}f\right)\left(R_i\right)={\int }_{R_j\in SO\left(3\right):\langle v\left(R_i\right),v\left(R_j\right)\rangle >1-h}{\mathcal{T}}_{R_i,R_j}f\left(R_j\right)d{R}_j,$$ (A.22)

We refer to ${\mathcal{C}}_h$, ${\mathcal{O}}_h$, and ${\mathcal{T}}_h$ as the local common lines operator, the local orthographic lines operator, and the local parallel transport operator, respectively.

A.4. Preliminary spectral analysis of the local operators

The following lemma is key to the characterization of the maximal eigenspace of ${\mathcal{T}}_h$.

Lemma A.2. Each of the three columns of

$$F\left(R\right)=\left(\begin{array}{ccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \end{array}\right)R^{-1}=\left(\begin{array}{ccc}\hfill R_{11}\hfill & \hfill R_{21}\hfill & \hfill R_{31}\hfill \\ \hfill R_{12}\hfill & \hfill R_{22}\hfill & \hfill R_{32}\hfill \end{array}\right)$$ (A.23)

is an eigenfunction of both ${\mathcal{C}}_h$, ${\mathcal{O}}_h$, and ${\mathcal{T}}_h$, with

$$\left({\mathcal{C}}_{h}F\right)\left(R\right)=\frac{1}{4}hF\left(R\right),$$ (A.24)

$$\left({\mathcal{O}}_{h}F\right)\left(R\right)=-\left(\frac{1}{4}h-\frac{1}{8}{h}^2\right)F\left(R\right),$$ (A.25)

$$\left({\mathcal{T}}_{h}F\right)\left(R\right)=\left(\frac{1}{2}h-\frac{1}{8}{h}^2\right)F\left(R\right).$$ (A.26)

Proof Recalling that $U=R_i^{-1}{R}_j$ gives

$$F\left(R_j\right)=F\left(R_{i}U\right)=\left(\begin{array}{ccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \end{array}\right)U^{-1}{R}_i^{-1}=\left(\begin{array}{ccc}\hfill U_{11}\hfill & \hfill U_{21}\hfill & \hfill U_{31}\hfill \\ \hfill U_{12}\hfill & \hfill U_{22}\hfill & \hfill U_{32}\hfill \end{array}\right)R_i^{-1}.$$ (A.27)

Together with (A.16) we obtain

$${\mathcal{C}}_{R_i,R_j}F\left(R_j\right)=\frac{1}{1-{\left(U_{33}\right)}^2}\left(\begin{array}{c}\hfill U_{23}\hfill \\ \hfill -U_{13}\hfill \end{array}\right)(-U_{32}{U}_{31})\left(\begin{array}{ccc}\hfill U_{11}\hfill & \hfill U_{21}\hfill & \hfill U_{31}\hfill \\ \hfill U_{12}\hfill & \hfill U_{22}\hfill & \hfill U_{32}\hfill \end{array}\right)R_i^{-1}.$$ (A.28)

We note that

$$(-U_{32}{U}_{31})\left(\begin{array}{ccc}\hfill U_{11}\hfill & \hfill U_{21}\hfill & \hfill U_{31}\hfill \\ \hfill U_{12}\hfill & \hfill U_{22}\hfill & \hfill U_{32}\hfill \end{array}\right)=(-U_{32}{U}_{31}0)\left(\begin{array}{ccc}\hfill U_{11}\hfill & \hfill U_{21}\hfill & \hfill U_{31}\hfill \\ \hfill U_{12}\hfill & \hfill U_{22}\hfill & \hfill U_{32}\hfill \\ \hfill U_{13}\hfill & \hfill U_{23}\hfill & \hfill U_{33}\hfill \end{array}\right)={(I^3\times {\left(U^{-1}\right)}^3)}^T{U}^{-1}={\left[U(I^3\times {\left(U^{-1}\right)}^3)\right]}^T={(U^3\times I^3)}^T=(U_{23}-U_{13}0),$$

which, substituting in (A.28), results in

$$\begin{array}{cc}\hfill {\mathcal{C}}_{R_i,R_j}F\left(R_j\right)& =\frac{1}{1-{\left(U_{33}\right)}^2}\left(\begin{array}{c}\hfill U_{23}\hfill \\ \hfill -U_{13}\hfill \end{array}\right)(U_{23}-U_{13}0)R_i^{-1}\hfill \\ \hfill & =\frac{1}{1-z^2}\left(\begin{array}{ccc}\hfill y^2\hfill & \hfill -xy\hfill & \hfill 0\hfill \\ \hfill -xy\hfill & \hfill x^2\hfill & \hfill 0\hfill \end{array}\right)R_i^{-1},\hfill \end{array}$$ (A.29)

where U³ = (x y z)^T. Similarly,

$$\begin{array}{cc}\hfill {\mathcal{O}}_{R_i{R}_j}F\left(R_j\right)& =\frac{1}{1-{\left(U_{33}\right)}^2}\left(\begin{array}{c}\hfill U_{13}\hfill \\ \hfill U_{23}\hfill \end{array}\right)\left(U_{31}{U}_{32}\right)\left(\begin{array}{ccc}\hfill U_{11}\hfill & \hfill U_{21}\hfill & \hfill U_{31}\hfill \\ \hfill U_{12}\hfill & \hfill U_{22}\hfill & \hfill U_{32}\hfill \end{array}\right)R_i^{-1}\hfill \\ \hfill & =\frac{1}{1-{\left(U_{33}\right)}^2}\left(\begin{array}{c}\hfill U_{13}\hfill \\ \hfill U_{23}\hfill \end{array}\right){[{\left(U^{-1}\right)}^3-U_{33}{I}^3]}^T{U}^{-1}{R}_i^{-1}\hfill \\ \hfill & =\frac{1}{1-{\left(U_{33}\right)}^2}\left(\begin{array}{c}\hfill U_{13}\hfill \\ \hfill U_{23}\hfill \end{array}\right){(I^3-U_{33}{U}^3)}^T{R}_i^{-1}\hfill \\ \hfill & =\frac{1}{1-z^2}\left(\begin{array}{ccc}\hfill -z{x}^2\hfill & \hfill -zxy\hfill & \hfill x(1-z^2)\hfill \\ \hfill -zxy\hfill & \hfill -z{y}^2\hfill & \hfill y(1-z^2)\hfill \end{array}\right)R_i^{-1}.\hfill \end{array}$$ (A.30)

From (A.29) and (A.30) it follows that the integrals over SO(3) defining ${\mathcal{C}}_{h}F$ and ${\mathcal{O}}_{h}F$ in (A.20)–(A.21) collapse to the following integrals over S²:

$$\left({\mathcal{C}}_{h}F\right)\left(R_i\right)={\int }_{\mathit{Cap}\left(h\right)}\frac{1}{1-z^2}\left(\begin{array}{ccc}\hfill y^2\hfill & \hfill -xy\hfill & \hfill 0\hfill \\ \hfill -xy\hfill & \hfill x^2\hfill & \hfill 0\hfill \end{array}\right)dS{R}_i^{-1},$$ (A.31)

$$\left({\mathcal{O}}_{h}F\right)\left(R_i\right)={\int }_{\mathit{Cap}\left(h\right)}\frac{1}{1-z^2}\left(\begin{array}{ccc}\hfill -z{x}^2\hfill & \hfill -zxy\hfill & \hfill x(1-z^2)\hfill \\ \hfill -zxy\hfill & \hfill -z{y}^2\hfill & \hfill y(1-z^2)\hfill \end{array}\right)dS{R}_i^{-1},$$ (A.32)

where Cap(h) = {(x, y, z) ∈ S² : z > 1 − h} and dS is the uniform measure over S² satisfying ∫_S² dS = 1. In Spherical coordinates

$$x=\sin \theta \cos \varphi ,y=\sin \theta \sin \varphi ,z=\cos \theta ,$$

the cap is given by 0 ≤ ϕ < 2π and 0 ≤ θ < α, where cos α = 1−h and $dS=\frac{1}{4\pi }\text{sin}\theta d$θdϕ. In order to simplify (A.31)–(A.32) we calculate the following integrals using spherical coordinates and symmetry whenever possible:

$${\int }_{\mathit{Cap}\left(h\right)}\frac{xy}{1-z^2}dS={\int }_{\mathit{Cap}\left(h\right)}\frac{zxy}{1-z^2}dS={\int }_{\mathit{Cap}\left(h\right)}xdS={\int }_{\mathit{Cap}\left(h\right)}ydS=0,$$

$$\begin{array}{cc}\hfill {\int }_{\mathit{Cap}\left(h\right)}\frac{x^2}{1-z^2}dS& ={\int }_{\mathit{Cap}\left(h\right)}\frac{y^2}{1-z^2}dS=\frac{1}{2}{\int }_{\mathit{Cap}\left(h\right)}\frac{x^2+y^2}{1-z^2}dS=\frac{1}{2}{\int }_{\mathit{Cap}\left(h\right)}dS\hfill \\ \hfill & =\frac{1}{2}\frac{1}{4\pi }{\int }_0^{2\pi }d\varphi {\int }_0^{\alpha }\sin \theta d\theta =\frac{1}{4}(1-\cos \alpha )=\frac{1}{4}h,\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\int }_{\mathit{Cap}\left(h\right)}\frac{z{x}^2}{1-z^2}dS& ={\int }_{\mathit{Cap}\left(h\right)}\frac{z{y}^2}{1-z^2}dS=\frac{1}{2}{\int }_{\mathit{Cap}\left(h\right)}\frac{z(x^2+y^2)}{1-z^2}dS=\frac{1}{2}{\int }_{\mathit{Cap}\left(h\right)}zdS\hfill \\ \hfill & =\frac{1}{2}\frac{1}{4\pi }{\int }_0^{2\pi }d\varphi {\int }_0^{\alpha }\cos \theta \sin \theta d\theta =\frac{1}{8}(1-{\cos }^2\alpha )=\frac{1}{4}h-\frac{1}{8}{h}^2.\hfill \end{array}$$

Substituting the values of the integrals above into (A.31)–(A.32) gives

$$\begin{array}{cc}\hfill & \left({\mathcal{C}}_{h}F\right)\left(R_i\right)=\frac{1}{4}h\left(\begin{array}{ccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \end{array}\right)R_i^{-1}=\frac{1}{4}hF\left(R_i\right),\hfill \\ \hfill & \left({\mathcal{O}}_{h}F\right)\left(R_i\right)=-\left(\begin{array}{c}\hfill \frac{1}{4}h-\frac{1}{8}{h}^2\hfill \end{array}\right)\left(\begin{array}{ccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \end{array}\right)R_i^{-1}=-\left(\frac{1}{4}h-\frac{1}{8}{h}^2\right)F\left(R_i\right).\hfill \end{array}$$

Together with Lemma A.1 we have

$$\begin{array}{cc}\hfill \left({\mathcal{T}}_{h}F\right)\left(R_i\right)& =\left({\mathcal{C}}_{h}F\right)\left(R_i\right)-\left({\mathcal{O}}_{h}F\right)\left(R_i\right)=\frac{1}{4}hF\left(R_i\right)+\left(\frac{1}{4}h-\frac{1}{8}{h}^2\right)F\left(R_i\right)\hfill \\ \hfill & =\left(\frac{1}{2}h-\frac{1}{8}{h}^2\right)F\left(R_i\right),\hfill \end{array}$$

and the proof of the lemma is completed.

Note that from (A.16) it follows that f : $SO\left(3\right)\mapsto {\mathbb{R}}^2$ is an eigenfunction of the operator ${\mathcal{O}}_h$ satisfying

$$\left({\mathcal{O}}_{h}f\right)\left(R\right)=\lambda f\left(R\right)\mathrm{for}\mathrm{all}R\in SO\left(3\right),$$

iff Jf is an eigenfunction of the operator ${\mathcal{C}}_h$ satisfying

$$\left({\mathcal{C}}_{h}Jf\right)\left(R\right)=\lambda Jf\left(R\right)\mathrm{for}\mathrm{all}R\in SO\left(3\right).$$

Indeed, suppose $\left({\mathcal{O}}_{h}f\right)\left(R\right)=\lambda f\left(R\right)$ for all R ∈ SO(3); then

$$\begin{array}{cc}\hfill \left({\mathcal{C}}_{h}Jf\right)\left(R_i\right)& ={\int }_{\langle v\left(R_i\right),v\left(R_j\right)\rangle >1-h}{\mathcal{C}}_{R_i,R_j}Jf\left(R_j\right)d{R}_j\hfill \\ \hfill & ={\int }_{\langle v\left(R_i\right),v\left(R_j\right)\rangle >1-h}-J{\mathcal{O}}_{R_i,R_j}{J}^{-1}Jf\left(R_j\right)d{R}_j\hfill \\ \hfill & =-J{\int }_{\langle v\left(R_i\right),v\left(R_j\right)\rangle >1-h}{\mathcal{O}}_{R_i,R_j}f\left(R_j\right)d{R}_j=-\lambda Jf\left(R_j\right).\hfill \end{array}$$

The other direction The other direction of the “iff” statement is verified in a similar manner. We conclude that the three columns of JF(R) are also eigenfunctions of ${\mathcal{T}}_h$ with the same eigenvalue ${\lambda }_1\left(h\right)=\frac{1}{2}h-\frac{1}{8}{h}^2$. Overall, the multiplicity of the eigenvalue λ₁(h) of ${\mathcal{T}}_h$ is 6.

A.5. Complex structure of the parallel transport kernel

We return to the complex structure and regard the parallel transport kernel ${\mathcal{T}}_{R_i,R_j}$ as a mapping⁹ from $\mathbb{C}$ to $\mathbb{C}$. Since parallel transport maps o_ji to −o_ij (A.11)–(A.12), the complex structure implies that

$${\mathcal{T}}_{R_i,R_j}(U_{31}+ıU_{32})=-(U_{13}+ıU_{23}),$$ (A.33)

and we conclude that the single matrix element for ${\mathcal{T}}_{R_i,R_j}$ is

$${\mathcal{T}}_{R_i,R_j}=\frac{(U_{13}+ıU_{23})}{(U_{31}+ıU_{32})}.$$ (A.34)

We proceed to prove that the rotation ${\tilde{\theta }}_{ij}$ of (2.5)–(2.6) obtained by optimal alignment of the bases (2.3) is the same rotation angle of the parallel transport kernel. Establishing this fact would justify that the class averaging matrix H, which is computed from the image data, is indeed the (discretized version of the) local parallel transport operator. Comparing the expressions in (A.34) and (2.5)–(2.6), we conclude that the proof consists of verifying that the identity

$$-\frac{(U_{13}+ıU_{23})}{(U_{31}+ıU_{32})}=\frac{(U_{11}+U_{12})+ı(U_{21}+U_{12})}{\sqrt{{(U_{11}+U_{22})}^2+{(U_{21}+U_{12})}^2}}$$ (A.35)

holds for all U ∈SO(3) with v(U) ≠ ±(0, 0, 1)^T (the parallel transport operator is not defined for v(R_i) = ±v(R_j)). The sphere $S^3\subset {\mathbb{R}}^4$ is a double cover of SO(3), and by Euler's formula, for U ∈ SO(3) there corresponds a vector (a unit quaternion) (a, b, c, d) ∈ S³ (a² + b² + c² + d² = 1), unique up to its antipodal point (−a, −b, −c, −d), such that

$$U=\left(\begin{array}{ccc}\hfill a^2+b^2-c^2-d^2\hfill & \hfill 2bc-2ad\hfill & \hfill 2ac+2bd\hfill \\ \hfill 2bc+2ad\hfill & \hfill a^2-b^2+c^2-d^2\hfill & \hfill -2ab+2cd\hfill \\ \hfill -2ac+2bd\hfill & \hfill 2ab+2cd\hfill & \hfill a^2-b^2-c^2+d^2\hfill \end{array}\right).$$ (A.36)

Using Euler's formula (A.36), the right-hand side of (A.35) is given by

$$\frac{(U_{11}+U_{22})+ı(U_{21}-U_{12})}{\sqrt{{(U_{11}+U_{22})}^2+{(U_{21}-U_{12})}^2}}=\frac{2(a^2-d^2)+4ıad}{2(a^2+d^2)},$$

while the left-hand side is

$$\begin{array}{cc}\hfill -\frac{U_{13}+ıU_{23}}{U_{31}+ıU_{32}}& =-\frac{(U_{13}{U}_{31}+U_{23}{U}_{32})+ı(U_{23}{U}_{31}-U_{13}{U}_{32})}{U_{31}^2+U_{32}^2}\hfill \\ \hfill & =-\frac{-4(a^2-d^2)(b^2+c^2)-8ıad(b^2+c^2)}{4(a^2+d^2)(b^2+c^2)},\hfill \end{array}$$

which verifies that the identity (A.35) holds for all U ∈ SO(3) with v(U) ≠ ±(0, 0, 1)^T and the proof is completed.

A.6. Preliminary spectral analysis of the complex local parallel transport operator

In the complex structure, multiplication by J is equivalent to multiplication by ı, so the columns of JF (R) are linear combinations of the columns of F (R), and the multiplicity of the eigenvalue λ₁(h) of ${\mathcal{T}}_h$ is only 3 (instead of 6 over the reals). We have the following pair of lemmas.

Lemma A.3. The three functions ψ₁, ψ₂, ψ₃ : SO(3) ↦ $\mathbb{C}$ given by

$${\psi }_1\left(R\right)=R_{11}+ıR_{12},$$ (A.37)

$${\psi }_2\left(R\right)=R_{21}+ıR_{22},$$ (A.38)

$${\psi }_3\left(R\right)=R_{31}+ıR_{32}$$ (A.39)

are orthogonal eigenfunctions of ${\mathcal{T}}_h$ satisfying

$${\mathcal{T}}_h{\psi }_m={\lambda }_1\left(h\right){\psi }_m,m=1,2,3,$$ (A.40)

where

$${\lambda }_1\left(h\right)=\frac{1}{2}h-\frac{1}{8}{h}^2,$$ (A.41)

and

$${\Vert {\psi }_1\Vert }^2={\Vert {\psi }_2\Vert }^2={\Vert {\psi }_3\Vert }^2=\frac{2}{3}.$$ (A.42)

Proof. The fact that ψ₁, ψ₂, ψ₃ are eigenfunctions of with eigenvalue of ${\mathcal{T}}_h$ with eigenvalue ${\lambda }_1\left(h\right)=\frac{1}{2}h-\frac{1}{8}{h}^2$ follows immediately from (A.26 (Lemma A.2) and the complex structure. The orthogonality of the eigenfunctions and their normalization are verified through

$$\begin{array}{cc}\hfill {\int }_{SO\left(3\right)}F{\left(R\right)}^{T}F\left(R\right)dR& ={\int }_{SO\left(3\right)}R\left(\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill \\ \hfill 0\hfill & \hfill 0\hfill \end{array}\right)\left(\begin{array}{ccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \end{array}\right)R^{-1}dR\hfill \\ \hfill & ={\int }_{SO\left(3\right)}R(I-I^3{\left(I^3\right)}^T)R^{-1}dR={\int }_{SO\left(3\right)}(I-R^3{R}^{3T})dR\hfill \\ \hfill & =I-{\int }_{SO\left(3\right)}\left(\begin{array}{ccc}\hfill x^2\hfill & \hfill xy\hfill & \hfill xz\hfill \\ \hfill xy\hfill & \hfill y^2\hfill & \hfill yz\hfill \\ \hfill xz\hfill & \hfill yz\hfill & \hfill z^2\hfill \end{array}\right)dR=I-\frac{1}{3}I=\frac{2}{3}I,\hfill \end{array}$$

where R³ = (x y z)^T, and we used symmetry to calculate

$${\int }_{SO\left(3\right)}{x}^{2}dR=\frac{1}{3}{\int }_{SO\left(3\right)}(x^2+y^2+z^2)dR=\frac{1}{3}{\int }_{SO\left(3\right)}dR=\frac{1}{3}.$$

Lemma A.4. Suppose ψ₁, ψ₂, ψ₃ are the three eigenfunctions of ${\mathcal{T}}_h$ given in (A.37)–(A.39), and define Ψ : SO(3) ↦ ${\mathbb{C}}^3$ as

$$\Psi \left(R\right)=({\psi }_1\left(R\right),{\psi }_2\left(R\right),{\psi }_3\left(R\right))forallR\in SO\left(3\right).$$

Then,

$$\langle R_i^3,R_j^3\rangle =2\frac{\mid \langle \Psi \left(R_i\right),\Psi \left(R_j\right)\rangle \mid }{\Vert \Psi \left(R_i\right)\Vert \Vert \Psi \left(R_j\right)\Vert }-1$$ (A.43)

for all R_i,R_j ∈ SO(3).

Proof. We start the proof with an explicit computation of the absolute value of the Hermitian dot product between Ψ(R_i) and Ψ(R_j):

$$\begin{array}{cc}\hfill {\mid \langle \Psi \left(R_i\right),\Psi \left(R_j\right)\rangle \mid }^2& ={\mid \langle R_i^1+ıR_i^2,R_j^1+ıR_j^2\rangle \mid }^2={\mid (U_{11}+U_{22})+ı(U_{21}-U_{12})\mid }^2\hfill \\ \hfill & ={(U_{11}+U_{22})}^2+{(U_{12}-U_{21})}^2,\hfill \end{array}$$ (A.44)

where $U=R_i^{-1}{R}_j$. The right-hand side of (A.44) can be further simplified using Euler's formula (A.36):

$${(U_{11}+U_{22})}^2+{(U_{12}-U_{21})}^2=4{(a^2+d^2)}^2={(1+U_{33})}^2$$

for all U ∈ SO(3). Therefore,

$${\mid \langle \Psi \left(R_i\right),\Psi \left(R_j\right)\rangle \mid }^2={(1+U_{33})}^2.$$ (A.45)

In particular,

$$\Vert \Psi \left(R_i\right)\Vert =\Vert \Psi \left(R_j\right)\Vert =\sqrt{2},$$

because

$${\Vert \Psi \left(R_i\right)\Vert }^2=\langle \Psi \left(R_i\right),\Psi \left(R_i\right)\rangle =1+I_{33}=2.$$

We conclude that

$$\frac{\mid \langle \Psi \left(R_i\right),\Psi \left(R_j\right)\rangle \mid }{\Vert \Psi \left(R_i\right)\Vert \Vert \Psi \left(R_j\right)\Vert }=\frac{1+U_{33}}{\sqrt{2}\sqrt{2}}$$

or, equivalently,

$$\langle R_i^3,R_j^3\rangle =U_{33}=2\frac{\mid \langle \Psi \left(R_i\right),\Psi \left(R_j\right)\rangle \mid }{\Vert \Psi \left(R_i\right)\Vert \Vert \Psi \left(R_j\right)\Vert }-1,$$

and the proof is completed.

Appendix B. Hairy ball theorem in the case of a finite number of images

One may argue that we should not care too much about the hairy ball theorem, because the number of images n is finite, so it is always possible to remove an arbitrarily small spherical cap from the sphere that does not include any of the n viewing angles, and that the resulting chopped sphere can be combed, using, e.g., the tangent vector field f given in (3.1). We move on to explain that the hairy ball theorem affects the eigenvectors of the matrix H even when the number of images is finite, and that the above argument for chopping off the sphere fails already for moderate values of n.

To that end, recall that in the noise-free case, the underlying graph used to construct H is a neighborhood graph on S². It may be further assumed that an edge between P_i and P_j exists iff the angle between their viewing angles is less than or equal to α, that is, {i, j} ∈ E ⇔ v_i, v_j > cos α. In other words, tilting the molecule by less than α results in a projection image that is similar enough to be recognized as a neighbor of the original (nontilted) image. Consider now the union of n spherical caps of opening angle α centered at the viewing angles v₁, …, v_n. If this union of n spherical caps entirely covers the sphere, then it would be impossible to chop an arbitrarily small cap off the sphere without affecting the underlying graph and the matrix H. Since the surface area of a spherical cap with an opening angle α is 4π ${\text{sin}}^2\frac{\alpha }{2}$, the total surface area covered by all n caps cannot exceed $n4\pi {\text{sin}}^2\frac{\alpha }{2}$ (union bound). As the total surface area of the sphere is 4π, we see that a complete coverage of the sphere with random spherical caps is impossible for $n\le \frac{1}{{\text{sin}}^2\frac{\alpha }{2}}$. For such small values of n we do not “see” the topology of the sphere through the connectivity graph, and the hairy ball theorem would not be effective. However, we are much more interested in large values of n corresponding to large image data sets that we want to class average in order to increase the SNR.

For large values of n, the probability that the sphere is not fully covered is exponentially small. The coverage problem of the sphere by random spherical caps is considered in [25, Chapter 4, pp. 85–96]. Let Pr(n, α) be the probability that n random spherical caps of opening angle α cover the sphere. Though we are not familiar with the exact value of Pr(n, α) except for special values of α and n, it is easy to derive useful upper and lower bounds for Pr(n, α) as well as its asymptotic behavior in the limit n→∞. For example, the probability that the north pole is not covered by any cap is ${(1-{\text{sin}}^2\frac{\alpha }{2})}^n$. If the sphere is covered, then in particular the north pole is covered, and thus, a simple upper bound for Pr(n, α) is given by

$$\text{Pr}(n,\alpha )\le 1-{\left(1-{\text{sin}}^2\frac{\alpha }{2}\right)}^n.$$

A slightly more involved geometric argument [25] shows that a lower bound is given by

$$\text{Pr}(n,\alpha )\ge 1-\frac{4}{3}n(n-1){\text{sin}}^2\frac{\alpha }{2}{\left(1-{\text{sin}}^2\frac{\alpha }{2}\right)}^{n-1}.$$

Combining the lower and upper bounds yields

$$\underset{n\to \infty }{lim}\frac{\text{log}(1-\text{Pr}(n,\alpha ))}{n}=\text{log}\left(1-{\text{sin}}^2\frac{\alpha }{2}\right).$$

In particular, Pr(n, α) goes to 1 exponentially quickly as n→∞; that is,

$$1-\text{Pr}(n,\alpha )~e^{n\text{log}(1-{\text{sin}}^2\frac{\alpha }{2})}.$$

In other words, the hairy ball theorem affects the eigenstructure of H as soon as the number of images n is of the order of $\frac{1}{-\text{log}(1-{\text{sin}}^2\frac{\alpha }{2})}\left(~\frac{1}{{\text{sin}}^2\frac{\alpha }{2}}\text{for small}\alpha \right)$.