Abstract
As brain ventricles lose their ability to regulate the cerebrospinal fluid (CSF) pressure, serious brain conditions collectively named hydrocephalus can appear. By modelling ventricular dynamics with the laws of physics, dynamical instabilities are evidenced, caused by either CSF transport dysregulations or abnormal properties of the elasticity of the ependyma. We show that these instabilities would lead, in most cases, to dilation of the ventricles, establishing a close connection to hydrocephalus, or in some other cases to a ventricular contraction as observed in the slit ventricle syndrome. Signs seem to indicate the possibility of phase transitions occurring as a result of these instabilities, which might have important clinical consequences, such as the inability to recover a healthy state. Even so, our dynamical approach could allow the development of a unified view of these complex intracranial conditions along with a classification that might be clinically relevant.
Keywords: Hydrocephalus, Brain ventricles, Instabilities, Biomechanics, Thermodynamics
Introduction
Hydrocephalus [1] overlaps a series of medical conditions sharing a common feature: expansion of brain ventricles. The large amount of clinical knowledge about hydrocephalus arises from the powerful magnetic resonance imaging (MRI) technique allowing CSF flow measurements [2, 3]. The usual classification of hydrocephalus, based on clinical criteria [4], reflects their wide spectrum. According to this classification scheme, two major types of hydrocephalus are distinguished, referred to as non-communicating or communicating classes. The former type can be induced by a stenosis of the aqueduct of Sylvius (obstructive hydrocephalus) [5], resulting in an accumulation of liquid within the ventricles [6]. The latter type encompasses Normal Pressure Hydrocephalus [7], characterized by the Hakim triad [8] consisting of gait disturbance, incontinence and mental changes. For these classes, in spite of a “normal” CSF transport to other compartments, expansion of the ventricles occurs. Nevertheless, apart from well-identified situations such as trauma, meningitis or haemorrhage, the causes of communicating hydrocephalus remain puzzling.
To go beyond the clinical picture, a model of the enlargement of the ventricles is required. It first seems reasonable to keep the question of the mechanism of the condition connected to an adequate depiction of the intracranial dynamics. A first type of model often met in the literature involves electrical analogues of the intracranial dynamics [9]. In an attempt to completely describe the whole intracranial system, these models lead to an unavoidable structural complexity, making this kind of model difficult to exploit [10]. The most prominent problem arises certainly from the yet non-elucidated way any pathological behaviour manifests itself in the structure of electrical analogues. Other interesting attempts inspired by a biomechanical description of brain and ventricles focus on the consequences of the hydrocephalic state [11–13]. These models treat the brain as a poroviscoelastic continuum through which the cerebrospinal fluid diffuses [14]. Though these models account well for the effects of non-communicating hydrocephalus, such as development of brain oedema, they do not assume any precise mechanism.
A rigorous description of intracranial dynamics is needed to highlight two basic problems: determination of the steady-state configuration of the brain ventricles and the fundamental causes of the condition. The identification of the steady state of each compartment allows for the derivation of a linearized scheme describing the dynamics of small perturbations around the steady-state configuration. From this linear scheme can be deduced both stability studies and interpretation of the dynamics in terms of electrical analogues.
The physical description of the whole intracranial system is too complex a task to be carried out because of its complex anatomical structure, that is, the great number of interconnected compartments to deal with and the lack of knowledge of the coupling between the compartments. Nevertheless, as the ventricular space is the only one expanding, we felt it natural to focus solely on ventricles to understand hydrocephalus. A first approach built up in an earlier study [15] led to structural instabilities in simplified geometry of the ventricles controlled either by the elastic properties of the tissues or the CSF transport with likely connections to hydrocephalus. This first approach gave an unsatisfactory depiction of the dynamics: some aspects of these instabilities remained fuzzy, especially the very origin of the conductance threshold. A unified derivation of ventricular dynamics and related instabilities is carried out in this paper. We indeed propose a realistic description of ventricular dynamics from which both instabilities can be rigorously derived as bifurcations. These are shown to induce a loss of the ability of the system to regulate CSF pressure. We further establish connections with hydrocephalus and identify these instabilities as the theoretically fundamental causes of hydrocephalus.
The dynamics of brain ventricles
Motion equation of the ependyma
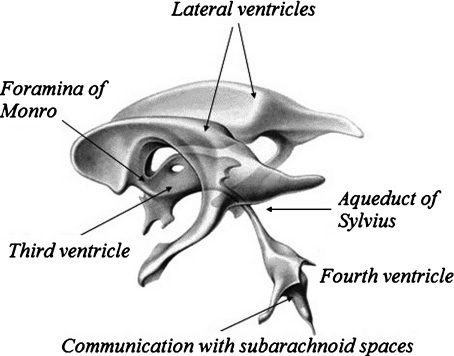
The ventricular space, schematized on Fig. 1, is composed of four CSF compartments communicating with each other. The lateral ventricles and the third ventricle exchange CSF through small apertures (foramina). The third ventricle is connected to the fourth by the aqueduct of Sylvius, this last ventricle ensuring CSF exchange with the subarachnoid space surrounding the brain and in the spinal cord. The ependyma is a thin elastic membrane of thickness about 500 μm [16] demarcating the ventricles. Its complex shape is modulated around a steady-state configuration, due to the arterial blood pulsating flow entering the brain.
Fig. 1.
Schematic view of the ventricular system. It is composed of four ventricles filled with cerebrospinal fluid. The two lateral ventricles are connected to the third one through the foramina of Monro. CSF exchange with the fourth ventricle occurs through the aqueduct of Sylvius, which is about 10–20 mm long with a diameter between 1.5 and 4 mm. Three apertures (the foramina of Magendie and the foramina of Luschka) control the communication with the subarachnoid space. Finally, the CSF diffusion distributed on the whole surface of the ependyma is limited by the permeability of the tissues to CSF
This steady-state configuration is an out of equilibrium state of the intracranial system. It is controlled by the steady CSF pressures within the compartments, the stress distribution within the brain and the CSF secretion process within the choroid plexus [17]. From a mathematical point of view, the ependyma is treated as a surface (Σ) of the Euclidean space and its motion is described by a small amplitude displacement field u(x ,t) defined on (Σ) . It is decomposed as a tangential motion (coordinates ua = (u1, u2)) and a normal displacement ξ =n · u such that u (x ,t) = uaea + ξn.
Our method for the derivation of the motion equation of the ependyma comes from the laws of thermodynamics, namely the first one. The internal energy of the ependyma/ventricular CSF system is governed by the functional of the displacement field,
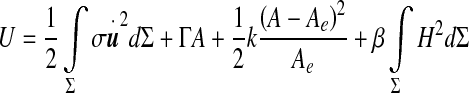 |
1 |
It comprises a kinetic energy contribution from the moving ependyma (with σ the ependymal mass per unit area) and a potential energy grouping the interfacial and elastic contributions. These terms form a Helfrich-like functional [18], composed of an interfacial energy governed by the CSF interfacial tension Γ [19], a stretching elasticity contribution (modulus k with units of energy per area) and a bending elasticity [20] contribution (bending stiffness β with units of energy). The stretching term, if alone, would constrain the ependyma to its equilibrium area Ae. The last term, depending functionally on the squared mean curvature H2 of the moving ependyma, is the Willmore functional [21–23]. The steady-state configurations are solutions of a highly non-linear equation obtained through a minimization of the potential energy in (1) with a constrained ventricular volume. The rigorous motion equation of the ependyma can be derived by varying the energy (1) with respect to the appropriate degrees of freedom and imposing energy dissipation (viscous damping of the motion). We can equivalently derive it more “intuitively” from the first law of thermodynamics. The main influence (and complication) of the Willmore term relies then on both polynomials of the mean curvature and a bi-Laplacian term (involving the displacement field) usually developed from the theory of elastic envelopes. A first simplification of the dynamics consists in dropping the bi-Laplacian terms in the limit of small bending stiffness or sufficiently large areas (or high radii of curvature) obeying the condition 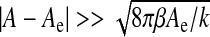 . This yields in fact a major simplification of the dynamical equations. A second simplification arises from the condition of small amplitude displacement fields allowing a linearization of the motion equation of the ependyma around its steady-state configuration.
. This yields in fact a major simplification of the dynamical equations. A second simplification arises from the condition of small amplitude displacement fields allowing a linearization of the motion equation of the ependyma around its steady-state configuration.
The first law of thermodynamics, which states that the total energy of a system is conserved, is written as
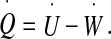 |
2 |
In this equation, the left-hand side is the heat power dissipated within the biological tissues composing the ependyma (tissues identical to pia mater) due to the friction forces (η is a friction coefficient per unit mass) which reads
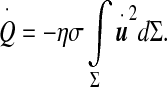 |
3 |
On the right-hand side, the term 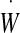 is the work per unit time of both internal and external forces exerted by both the ventricular CSF and the moving brain on the ependyma. It can be written as
is the work per unit time of both internal and external forces exerted by both the ventricular CSF and the moving brain on the ependyma. It can be written as
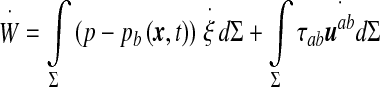 |
4 |
The first term groups the contribution from the pressure forces (p within the ventricles) and the “pressure” pb arising from the normal component of the stress tensor σij within the brain matter. The tangential part (shear stress) of this tensor, τab, couples to the strain rate tensor 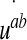 in the second integral.
in the second integral.
Neglecting the contribution from the bending energy 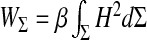 (by remembering that the mean curvature H is sufficiently small) and introducing the modulation δp (δpb) of the pressure p (pb) around its steady value
(by remembering that the mean curvature H is sufficiently small) and introducing the modulation δp (δpb) of the pressure p (pb) around its steady value 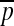 (
(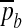 ), we are led to the projections of the motion equation along the normal direction (5) and the tangent plane (6):
), we are led to the projections of the motion equation along the normal direction (5) and the tangent plane (6):
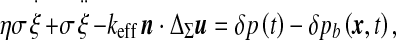 |
5 |
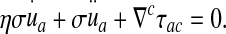 |
6 |
The final equation of motion (5) rules the macroscopic dynamics of a system composed of the ventricular CSF interacting with the viscoelastic ependyma. The Laplacian term involved arises from the definition of the steady mean curvature 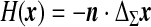 , and its coefficient, the effective stretching modulus
, and its coefficient, the effective stretching modulus 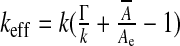 , derives from a linearization of the complete, nonlinear equation written from (2), where we replaced the area A by its steady-state value
, derives from a linearization of the complete, nonlinear equation written from (2), where we replaced the area A by its steady-state value 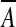 . There is a simpler way to derive this effective modulus, allowing us to highlight its physical significance. From the internal energy expression associated with a steady-state configuration (kinetic energy dropped) we retain the only area-dependent terms and calculate the variation of this energy δU upon any area variation δA, that is
. There is a simpler way to derive this effective modulus, allowing us to highlight its physical significance. From the internal energy expression associated with a steady-state configuration (kinetic energy dropped) we retain the only area-dependent terms and calculate the variation of this energy δU upon any area variation δA, that is 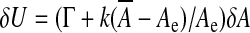 . This result evidences an effective stretching modulus keff = δU/δA which might also be regarded from a thermodynamical point of view as an effective interfacial tension. The right hand side of Eq. 5 is the normal projection of the force per unit area
. This result evidences an effective stretching modulus keff = δU/δA which might also be regarded from a thermodynamical point of view as an effective interfacial tension. The right hand side of Eq. 5 is the normal projection of the force per unit area 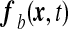 exerted on the ependyma by the stress field within the brain matter. This force contains a shear stress contribution and a normal “pressure force”
exerted on the ependyma by the stress field within the brain matter. This force contains a shear stress contribution and a normal “pressure force” 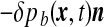 , opposing the CSF pressure-induced force
, opposing the CSF pressure-induced force 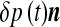 . This relation contains a diffusion-like term associated with the Laplace–Beltrami operator [24] ΔΣ on the ependyma. It exhibits an effective diffusion constant D = keff /ησ proportional to the effective stretching modulus
. This relation contains a diffusion-like term associated with the Laplace–Beltrami operator [24] ΔΣ on the ependyma. It exhibits an effective diffusion constant D = keff /ησ proportional to the effective stretching modulus 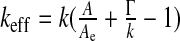 depending on the steady area A/Ae (in units of the equilibrium area) of the ependyma. This effective parameter, associated with the steady-state configurations of the ependyma, originates mainly from the interaction between CSF and the ependyma and the linearization procedure. It should be noticed that the relation between diffusion constant D and the effective modulus keff has an algebraic nature.
depending on the steady area A/Ae (in units of the equilibrium area) of the ependyma. This effective parameter, associated with the steady-state configurations of the ependyma, originates mainly from the interaction between CSF and the ependyma and the linearization procedure. It should be noticed that the relation between diffusion constant D and the effective modulus keff has an algebraic nature.
This equation can be viewed as an “effective” Laplace–Young law [25] describing the way the CSF surface is constrained to curve to adapt to the shape of the ependyma. Indeed, this last equation leads to
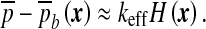 |
7 |
This last condition defines the steady-state configuration of the ependyma through its mean curvature H in the retained approximation (neglecting the bending energy contribution). Having the form of a Laplace–Young equation, it shows clearly that the effective modulus is to be thought of as an interfacial tension. This interpretation is fundamental in the following discussions of the instabilities.
CSF transport equation
The equation of motion (5) must be completed by a CSF mass conservation equation accounting for the fluid exchange between ventricles and outer compartments. This conservation equation relates the ventricular volume modulation 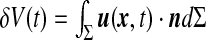 to the CSF exchange and secretion processes. Simplification of this equation depends on the nature of the CSF flow between compartments.
to the CSF exchange and secretion processes. Simplification of this equation depends on the nature of the CSF flow between compartments.
The most important CSF exchange process holds between ventricles and subarachnoid spaces (pressure δps) through the aqueduct of Sylvius (in fact this conduit connects the fourth ventricles to the other ventricles). While the simplest and most encountered way to model the CSF flow through the aqueduct of Sylvius would be to take it as a Poiseuille flow, we will show here that it seems an unreasonable assumption.
For a fluid flow to obey the law of Poiseuille, the following criteria must be met: it must be laminar, steady, incompressible, irrotational, and the walls delineating the flow are to be rigid. Although the CSF flow is incompressible to a good approximation, other hypotheses are not necessarily verified. Indeed, related work held on pulsatile flows in stenotic geometries [26] indicated the possibilities for vortices, and possibly turbulences, to develop. It should be noted that with the heart acting as a pump, pressure gradients of fluid flows through the body are inverted with every beat. This makes blood and CSF flows oscillatory, and thus renders them unable to develop a steady state. They must therefore be described with a more accurate law than that of Poiseuille. Womersley [27] studied these flows, albeit still considering rigid walls. The analytical expression of the hydrodynamic conductance of the flow can be deduced from his work and yields:
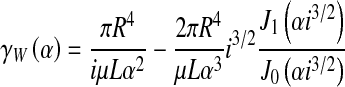 |
8 |
where 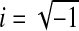 , R is the radius of the aqueduct, L its length, μ is the dynamic viscosity of CSF, Jk(x) denotes Bessel functions of the first kind, and
, R is the radius of the aqueduct, L its length, μ is the dynamic viscosity of CSF, Jk(x) denotes Bessel functions of the first kind, and 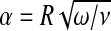 is a dimensionless number, called the Womersley number. It is expressed as a function of the angular frequency ω of the heartbeat and the CSF kinematic viscosity ν. This conductance is a complex number, but we shall focus on the real part, as it is the one we can compare to the Poiseuille conductance (which simply reads
is a dimensionless number, called the Womersley number. It is expressed as a function of the angular frequency ω of the heartbeat and the CSF kinematic viscosity ν. This conductance is a complex number, but we shall focus on the real part, as it is the one we can compare to the Poiseuille conductance (which simply reads 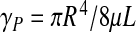 ).
).
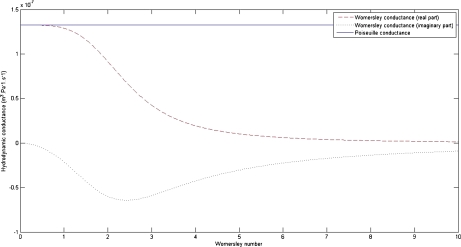
It can be easily shown that as the frequency of the oscillations vanishes (and so the Womersley number α vanishes as well), the Womersley conductance γW is exactly equal to that deduced from the law of Poiseuille. Let us now assess both conductances: for a typical and healthy CSF flow through the aqueduct [28], with radius R ≈ 1.5 mm, viscosity ν ≈ 10 − 6 m2 s − 1 and excited at the heartbeat frequency ω ≈ 2π s − 1, we obtain α ≈ 4. Taking the length of the aqueduct L ≈ 15 mm, the Poiseuille conductance is estimated as 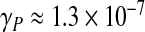 m3 s − 1 Pa − 1, and the real part of the Womersley conductance is
m3 s − 1 Pa − 1, and the real part of the Womersley conductance is 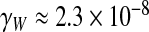 m3 s − 1 Pa − 1, evidencing a difference of one order of magnitude between them (Fig. 2).
m3 s − 1 Pa − 1, evidencing a difference of one order of magnitude between them (Fig. 2).
Fig. 2.
Plot of the hydrodynamic conductances vs the Womersley number. The hydrodynamic conductances of a healthy aqueduct of Sylvius have been computed, deduced from the law of Poiseuille (straight line), and from the Womersley description, with both real (dashed) and imaginary (dotted) parts included. The Poiseuille conductance remains constant for any Womersley number: it does not take into account the oscillatory nature of the flow. The values of the parameters used to calculate the conductances were displayed previously. A normal flow through a healthy aqueduct should have a Womersley number approximately equal to 4, highlighting a large difference between the conductances deduced from both laws
We can consider that the conductance of the aqueduct involved in our model is more precisely given by the law of Womersley (γaq ≈ γW (α ≈ 4)), in spite of some limitations: the curvature of the aqueduct, although low, is totally neglected, as well as its elasticity (it is supposed rigid). Taking into account its curvature would modify the characteristics of the flow so that vortices would appear which, if in a sufficiently high density, would possibly render the flow turbulent.
An additional exchange process with brain (pressure fluctuation δpb) is also present through the whole ependymal surface. Indeed, due to the porosity of this envelope, the CSF flow is associated with a velocity field given by Darcy’s law 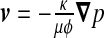 where κ is the permeability of the ependyma, ϕ its porosity, μ the dynamic viscosity of CSF, and
where κ is the permeability of the ependyma, ϕ its porosity, μ the dynamic viscosity of CSF, and 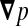 the pressure gradient between the ventricles and the neighbouring brain matter. The resulting total flow rate through the ependymal surface is
the pressure gradient between the ventricles and the neighbouring brain matter. The resulting total flow rate through the ependymal surface is 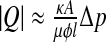 , where A is the area of the ependyma, l its thickness, and Δp the pressure difference through both ends. The corresponding hydrodynamic conductance is then
, where A is the area of the ependyma, l its thickness, and Δp the pressure difference through both ends. The corresponding hydrodynamic conductance is then 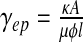 . The CSF crossing the ependyma saturates the brain pores neighbouring the ventricles, and will barely flow throughout the brain matter, except in some extreme conditions. In fact, this flow is also ruled by Darcy’s law, with an associated conductance of exactly the same expression. It is now clear that for sufficiently low pressure gradients and under normal conditions, the flow rate of CSF throughout the brain parenchyma will be insignificant. On the contrary, in the case of an extreme hydrocephalus, the brain being under severe compressive stress, its thickness is reduced, resulting in a larger amount of CSF flowing through the parenchyma. The sum of the conductances ruling both flows is the total conductance γ = γaq + γep . An additional term accounting for the CSF secretion process in the choroid plexus [17] is also required. Its component modulated by the pressure variations reads in first approximation δS(t) ≈ γCδp(t) with a constant γC > 0, usually referred to as secretion conductance [9] and connected to CSF synthesis kinetics. Exact calculation of the secretion conductance is difficult (and unnecessary here) since it requires a complete description of the secretion process. Retaining a positive γC ensures that increasing secretion leads to an increase in CSF pressure and vice versa. The third main equation of our model finally reads
. The CSF crossing the ependyma saturates the brain pores neighbouring the ventricles, and will barely flow throughout the brain matter, except in some extreme conditions. In fact, this flow is also ruled by Darcy’s law, with an associated conductance of exactly the same expression. It is now clear that for sufficiently low pressure gradients and under normal conditions, the flow rate of CSF throughout the brain parenchyma will be insignificant. On the contrary, in the case of an extreme hydrocephalus, the brain being under severe compressive stress, its thickness is reduced, resulting in a larger amount of CSF flowing through the parenchyma. The sum of the conductances ruling both flows is the total conductance γ = γaq + γep . An additional term accounting for the CSF secretion process in the choroid plexus [17] is also required. Its component modulated by the pressure variations reads in first approximation δS(t) ≈ γCδp(t) with a constant γC > 0, usually referred to as secretion conductance [9] and connected to CSF synthesis kinetics. Exact calculation of the secretion conductance is difficult (and unnecessary here) since it requires a complete description of the secretion process. Retaining a positive γC ensures that increasing secretion leads to an increase in CSF pressure and vice versa. The third main equation of our model finally reads
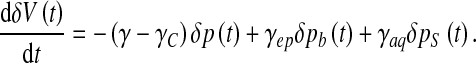 |
9 |
This last equation is closely related to observation since it involves CSF flow through the aqueduct and the transependymal diffusion which could be accessible through flow MRI [2, 4].
Introducing the compliance of the ventricular compartment allows us to write Eq. 9 as a pressure evolution equation. Adopting a physical point of view, we define compliance as the susceptibility connecting the ventricular CSF volume variations to its pressure modulations. More precisely, within the linear response approximation, it is defined as the time Fourier transform of the corresponding response, that is, the functional derivative C(t − t′) = δV(t)/δp(t′) or equivalently, the volume variation is the convolution of the pressure variations with the response function C(t). This approach leads naturally to a frequency-dependent compliance (dynamical compliance). It shows also that both the evoked response function and the compliance are completely determined by the Green’s functions [29] of the motion equation of the ventricles (5). Thus, compliance is no longer an arbitrary fitting parameter, but rather a function of the biomechanical properties of the intracranial system, which can be estimated. The vanishing frequency limit of the dynamical compliance defines the static compliance,
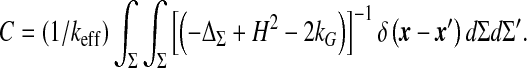 |
10 |
This depends on the area of the ependyma, the stretching elasticity modulus, the interfacial tension Γ, and an always positive factor given by the double integration over the ependymal area. This last factor expresses the dependence of the brain ventricles’ compliance upon the ependymal shape, since it appears as a functional of the steady-state mean curvature H and Gaussian curvature kG of the ependyma. The action of the inverted differential operator within the integrals on the Dirac distribution is nothing but the Green’s function (its static limit) of the motion equation of the ventricles. The differential operator involved in the Green’s function exhibits an interesting connection with the Dirac operator on a curved manifold [30]. Its interest is magnified in the assessment of the response of the ventricles to the physiological noise or equivalently, the effect of fluctuations of the ependyma which might be clinically relevant. Equation 10 gives the most general expression of the ventricular compliance (or any closed deformable compartment). The simplest case of spherical ventricles corresponds to a compliance 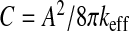 . The compliance given by (10) allows then a complete characterization of the compartment under study: first, dynamical through the Green’s function depending on biophysical properties, such as the viscoelasticity of tissues and of the liquid confined within them, and second, geometrical, through the steady-state shape of the surface Σ, that is, its curvatures. These considerations point out the quantitative influence of the shape of the ependyma on ventricular dynamics. This important result should have a deeper physical significance which remains to be highlighted. It should be noticed that the compliance scales always as 1/keff, whatever the shape of the ependyma, be it simple (e.g., a sphere) or more complex.
. The compliance given by (10) allows then a complete characterization of the compartment under study: first, dynamical through the Green’s function depending on biophysical properties, such as the viscoelasticity of tissues and of the liquid confined within them, and second, geometrical, through the steady-state shape of the surface Σ, that is, its curvatures. These considerations point out the quantitative influence of the shape of the ependyma on ventricular dynamics. This important result should have a deeper physical significance which remains to be highlighted. It should be noticed that the compliance scales always as 1/keff, whatever the shape of the ependyma, be it simple (e.g., a sphere) or more complex.
The above mentioned relationship between the volume and the pressure variations can be given the form of a series expansion of the pressure and its derivatives. With heartbeats being the excitation of the system, and their frequency being sufficiently low (approximately 1 Hz), the ventricular pressure will vary slowly. This allows us to truncate this expansion to the first order, leading to the pressure fluctuations dynamics equation
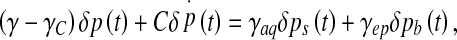 |
11 |
governed by a natural frequency scale
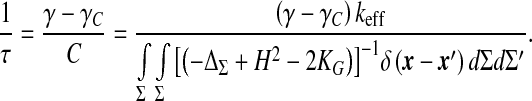 |
12 |
This equivalently defines the time scale τ for the elimination of pressure fluctuations. Equation 10 replaces Eq. 9 in the low excitation frequency limit. If needed, corrections to that scheme can be obtained straightforwardly by adding the higher-order derivatives we dropped in the volume expansion. Whatever the refinement of the simplest model given by (11), this characteristic time τ is always present, and its algebraic nature, clearly evidenced in (12), generates dynamical instabilities analyzed in the next section.
Evidence for bifurcations of ventricular dynamics
Elastic and transport instabilities
The characteristic time τ appearing in Eq. 12 being of algebraic nature, structural instabilities are expected to occur if it becomes negative, that is, either for a total conductance γ < γC (and keff > 0) or for keff < 0 (but γ < γC). This can be deduced from the solutions of this equation, taking the form δp(t) ∝ e − t/τ: with τ > 0, pressure fluctuations are quickly damped, whereas they grow exponentially with time as τ becomes negative. The first bifurcation (γ < γC, keff > 0), controlled by the hydrodynamic conductances of the CSF pathways, will be referred to as the “transport instability”. The second one (γ < γC, keff > 0), governed by the elastic properties of the ependyma, is called the “elastic instability”. Intuitively, the transport instability can be understood as a competition between CSF secretion and its evacuation through the aqueduct and the ependyma: the evacuation process cannot overcome its secretion, and CSF accumulates within the ventricles. The elastic instability is, on the contrary, not intuitive, since it proceeds from the competing effect of the elastic modulus k and the CSF interfacial tension Γ, but with normal CSF evacuation abilities. We notice that the elastic instability becomes evident in the motion equation of the ependyma (5). Indeed, a diffusion process of the displacement field is evidenced, with an algebraic diffusion constant D = keff /ησ, this last one being negative when keff < 0.
It is clear from Eq. 11 that both instabilities share a common feature, that is, pressure fluctuations develop exponentially inside the ventricles: they lose their ability to regulate the CSF pressure. Obviously, the pressure does not diverge to infinity, as our linear stability analysis holds for small fluctuations and is only valid for short time spans. As the pressure grows, non-linear terms will act to saturate the pressure evolution toward a fixed, anomalous value. It is, however clear that both this intracranial pressure disorder and its subsequent abnormal high or low value have to be thought of as pathological behaviours. Connections of our model to clinical situations have to be handled in this way: it can be directly seen from Eq. 5 that, for both unstable regimes, the unbounded pressure evolution leads to unbounded displacement fields 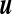 . As a consequence, ventricular dilations or contractions occur depending on the “initial” pressure conditions within the ventricles. We suggest that ventricular dilations would connect our instabilities to hydrocephalus. But, the most unanticipated result is the contraction likely to occur in some conditions. Contractions of ventricles have been observed and are clinically described as “slit ventricle syndrome” [31]. Except the fact that slit ventricle syndrome may occur due to CSF overdrainage and as a consequence of a hydrocephalus, there was no physical evidence for its intrinsic connection with this condition. Our approach indicates that it would proceed from the instabilities of the ependymal dynamics. Unexpectedly, our model of intracranial dynamics unifies hydrocephalus and slit ventricle syndrome by associating them with two symmetrical processes, dilation or contraction of ventricles.
. As a consequence, ventricular dilations or contractions occur depending on the “initial” pressure conditions within the ventricles. We suggest that ventricular dilations would connect our instabilities to hydrocephalus. But, the most unanticipated result is the contraction likely to occur in some conditions. Contractions of ventricles have been observed and are clinically described as “slit ventricle syndrome” [31]. Except the fact that slit ventricle syndrome may occur due to CSF overdrainage and as a consequence of a hydrocephalus, there was no physical evidence for its intrinsic connection with this condition. Our approach indicates that it would proceed from the instabilities of the ependymal dynamics. Unexpectedly, our model of intracranial dynamics unifies hydrocephalus and slit ventricle syndrome by associating them with two symmetrical processes, dilation or contraction of ventricles.
Bifurcation diagram
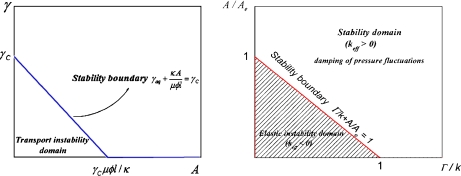
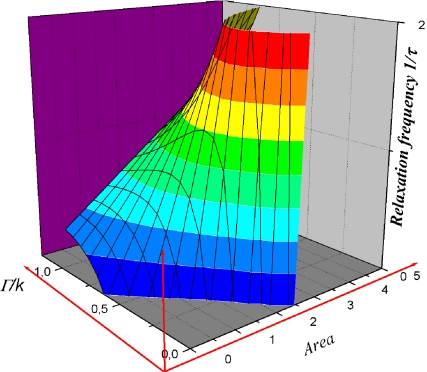
Bifurcation diagrams are depicted in Fig. 3a and b. The transport instability condition reported in Fig. 3a can be regarded as an area-dependent critical threshold imposed on the conductance γaq of the aqueduct. This shows that stability corresponds to sufficiently large areas or conductances. In a similar way, the critical elasticity conditions reported on Fig. 3b show that stability is favoured by sufficiently large areas and/or Γ/k ratios. It can be more easily understood if we notice that high values of Γ make it very difficult to change the area of the ependyma-CSF interface (higher cost in energy). In fact, this plot is the section of the plane 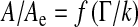 defined by the more complex surface plotted in Fig. 4 giving the influence of the area and biophysical properties of the ependyma on the relaxation frequency 1/τ. Both instabilities are associated with divergent susceptibilities: on the elastic stability boundary-line (keff = 0) the compliance is infinite. Similarly, for the transport instability the characteristic time τ = C/(γ − γC ) diverges. If the compliance has been clearly defined as a susceptibility, we yet have to determine if the characteristic relaxation time τ behaves like a susceptibility as well.
defined by the more complex surface plotted in Fig. 4 giving the influence of the area and biophysical properties of the ependyma on the relaxation frequency 1/τ. Both instabilities are associated with divergent susceptibilities: on the elastic stability boundary-line (keff = 0) the compliance is infinite. Similarly, for the transport instability the characteristic time τ = C/(γ − γC ) diverges. If the compliance has been clearly defined as a susceptibility, we yet have to determine if the characteristic relaxation time τ behaves like a susceptibility as well.
Fig. 3.
Elastic and transport instability domains. Left Localization of the transport instability domain in the conductance (γ) – area (A) plane. Below the conductance threshold γC, the transport instability develops (that is, under the straight line). This instability threshold amounts to a critical conductance of the aqueduct 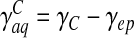 decreasing when the area of the ependyma increases. In the instability domain, CSF pressure regulation ability is lost. Right The elastic instability domain in the plane Γ/k + A/Ae < 1 corresponds to the shaded area. In the elastic stability domain, located above the stability boundary line keff = 0, CSF pressure fluctuations are damped, while they develop exponentially in the instability domain
decreasing when the area of the ependyma increases. In the instability domain, CSF pressure regulation ability is lost. Right The elastic instability domain in the plane Γ/k + A/Ae < 1 corresponds to the shaded area. In the elastic stability domain, located above the stability boundary line keff = 0, CSF pressure fluctuations are damped, while they develop exponentially in the instability domain
Fig. 4.
3-D plot of the variations of the relaxation frequency with the biophysical parameters of the CSF-ependyma system (Γ, k). For given biophysical properties (Γ, k fixed), the evolution of the relaxation frequency with the area A is obtained by a section of this surface defined by the a vertical plane Γ/k = constant. The elastic stability boundary corresponds to the section by the plane 1/τ = 0
In fact, this time scale is closely connected to the Green’s functions of the equation ruling the pressure fluctuation dynamics (Eq. 11). We rewrite Eq. 11 as
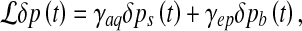 |
13 |
where the linear differential operator 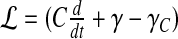 acts on the pressure fluctuations δp(t). The Green’s function G(t) of this differential equation is obtained from
acts on the pressure fluctuations δp(t). The Green’s function G(t) of this differential equation is obtained from
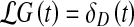 |
14 |
where δD(t) denotes the Dirac delta function. Taking the Fourier transform of this equation then yields the transfer function of the ventricular pressure dynamics,
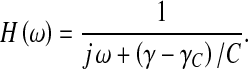 |
15 |
This is an equation of a linear first order filter whose vanishing frequency limit is clearly divergent at the crossing of the transport stability boundary (γ → γC). This transfer function thus behaves as a susceptibility in the sense of phase transitions where the static susceptibility δψ/δh connecting the variations of the order parameter ψ to those of its conjugate field h diverges at the transition. As usual phase transitions are driven by temperature; the most useful analogy in our case consists in treating the conductance γ as temperature and the critical conductance γC as the critical temperature TC. As a susceptibility, our transfer function connects the intraventricular pressure variations to the pressure variations in outer compartments. Beyond this useful operational analogy, the evidenced susceptibilities suggest a likely interpretation of our bifurcations as phase transitions of the intracranial system. The main question raised by such an interpretation regards the very nature of these phase transitions: Is there any broken symmetry process, as in the study of thermodynamics of phase transitions?
Parameter estimation
This section is devoted to the assessment of the parameters of the model from relevant available data. Retaining the experimental stretching stiffness k ≈ 0.19 N/mm reported for pia mater [32], tissue of the same nature as the ependyma, a Poisson ratio ν = 0.36 and their connection [20] with Young’s modulus E satisfying k ≈ 12πEl/(1 − ν2) we are led to an estimate of the Young’s modulus of the ependyma E ≈ 0.92.104 Pa. Keeping in mind that the ependyma is made up of soft tissues, the value we find for E is in good agreement with the range of those of elastic materials. As keff ≥ k, the compliance C of a steady-state configuration—close to the sphere—is bounded by a maximal value, 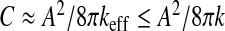 . According to the values of the preceding biophysical parameters and by adopting a “healthy” typical ependymal area A ≈ 50 cm2 (as calculated by Balédent and Bouzerar, using MRI analysis and the software Mimics), the maximal compliance is about
. According to the values of the preceding biophysical parameters and by adopting a “healthy” typical ependymal area A ≈ 50 cm2 (as calculated by Balédent and Bouzerar, using MRI analysis and the software Mimics), the maximal compliance is about 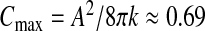 ml/mmHg, to be compared to the typical value of the compliance reported in the literature C ≈ 0.25 ml/mmHg [33]. From this last value, we can estimate the effective stretching modulus
ml/mmHg, to be compared to the typical value of the compliance reported in the literature C ≈ 0.25 ml/mmHg [33]. From this last value, we can estimate the effective stretching modulus 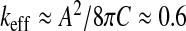 N/mm. In normal conditions, with the interfacial tension [34] Γ ≈ 64 mJ/m2, the ratio Γ/k can be neglected. We are thus led to the area ratio A/Ae ≈ 1 + keff/k ≈ 4, corresponding to an equilibrium area Ae ≈ 13 cm2. The maximal compliance we were led to requires a minimal stretching effective modulus keff min ≈ 0.23 N/mm, corresponding to a minimal size of the ventricles A min /Ae ≈ 1.2 (up to the accuracy of the measurements reported in [32]).
N/mm. In normal conditions, with the interfacial tension [34] Γ ≈ 64 mJ/m2, the ratio Γ/k can be neglected. We are thus led to the area ratio A/Ae ≈ 1 + keff/k ≈ 4, corresponding to an equilibrium area Ae ≈ 13 cm2. The maximal compliance we were led to requires a minimal stretching effective modulus keff min ≈ 0.23 N/mm, corresponding to a minimal size of the ventricles A min /Ae ≈ 1.2 (up to the accuracy of the measurements reported in [32]).
A typical value of the hydrodynamic conductance of an open, healthy aqueduct (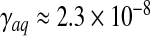 m3 s − 1 Pa − 1 assessed in the Womersley regime) and a CSF secretion conductance of about
m3 s − 1 Pa − 1 assessed in the Womersley regime) and a CSF secretion conductance of about 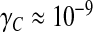 m3 s − 1 Pa − 1 reported by Czosnyka et al. [35] lead to a ratio (γ − γC)/C ≈ 14.5 s − 1. This yields a typical relaxation time τ ≈ 0.07 s to be compared to a heartbeat period of 1 s. The minimal value of the relaxation frequency is (γ − γC)/C max ≈ 5.5 s − 1 or equivalently the maximal relaxation time τ max ≈ 0.18 s.
m3 s − 1 Pa − 1 reported by Czosnyka et al. [35] lead to a ratio (γ − γC)/C ≈ 14.5 s − 1. This yields a typical relaxation time τ ≈ 0.07 s to be compared to a heartbeat period of 1 s. The minimal value of the relaxation frequency is (γ − γC)/C max ≈ 5.5 s − 1 or equivalently the maximal relaxation time τ max ≈ 0.18 s.
We can finally compare the parameter values in healthy and pathological situations. MRI data analysis carried out on a population of ten hydrocephalic subjects (Balédent and Bouzerar) leads to an average ependymal area A′ ≈ 300 cm2 (±78 cm2), that is, about six times greater than the healthy area A. This amounts to a static compliance C′ = 6C, six times as large as the “healthy” value since 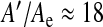 . This yields a relaxation time which is also six times greater (τ′ ≈ 0.42 s). Since the relaxation time corresponds to the required time for the ventricular dynamics to dampen pressure fluctuations, a larger relaxation time indicates that the CSF pressure regulation is less efficient. The gap between this time and the maximal time reinforces that conclusion. How should this be understood? Without referring to our instabilities, all that, can be said is that upon dilation, the pressure fluctuation damping process of the ventricles becomes less efficient (the lifetime of the fluctuations is increased). If the initial state of the brain ventricles corresponds to a normal size, the short lifetimes of the pressure fluctuations does not allow for the ventricles to dilate because of the damping of the fluctuations. In other words, inflation cannot arise spontaneously from healthy ventricles. Now, if instabilities are present, the situation is drastically different: the change in sign of the relaxation frequency indicates an amplification of the pressure fluctuations, now allowing for dilation. It is interesting to point out that dilation occurs for the ventricular system to recover a positive compliance (for the elastic instability) and normal pressure fluctuation damping conditions. No return to the initial state is then possible since the instability would again drive ventricles to a higher size. In that sense, our instabilities are phase transitions.
. This yields a relaxation time which is also six times greater (τ′ ≈ 0.42 s). Since the relaxation time corresponds to the required time for the ventricular dynamics to dampen pressure fluctuations, a larger relaxation time indicates that the CSF pressure regulation is less efficient. The gap between this time and the maximal time reinforces that conclusion. How should this be understood? Without referring to our instabilities, all that, can be said is that upon dilation, the pressure fluctuation damping process of the ventricles becomes less efficient (the lifetime of the fluctuations is increased). If the initial state of the brain ventricles corresponds to a normal size, the short lifetimes of the pressure fluctuations does not allow for the ventricles to dilate because of the damping of the fluctuations. In other words, inflation cannot arise spontaneously from healthy ventricles. Now, if instabilities are present, the situation is drastically different: the change in sign of the relaxation frequency indicates an amplification of the pressure fluctuations, now allowing for dilation. It is interesting to point out that dilation occurs for the ventricular system to recover a positive compliance (for the elastic instability) and normal pressure fluctuation damping conditions. No return to the initial state is then possible since the instability would again drive ventricles to a higher size. In that sense, our instabilities are phase transitions.
Another conclusion to be drawn regards the lower bound on the ventricular system size: we expect that ventricular areas smaller than A min might indicate a slit ventricle syndrome. Apart from the elastic instability, we notice that the compliance should not exceed the upper bound given by C max . The value of this upper bound is dependent on the mechanical moduli such as the Young’s modulus of tissues: since it is inversely proportional to this modulus, a large Young’s modulus E will result in a small C max . It is thus clear that the dynamics of brain ventricles requires materials that are not too rigid in order to operate efficiently.
Discussion
In our approach, both the elastic and the transport bifurcations of ventricular dynamics generate pathological states through the loss of CSF pressure regulation ability, reminiscent of some clinical features of hydrocephalus [36]. These instabilities are followed by a dilation process: they act as likely causes of hydrocephalus. But, contraction is also likely to occur under some conditions: our theory unifies slit ventricle syndrome and hydrocephalus on the basis of the reciprocity of the dilation and contraction processes. The natural reciprocity of these processes inspires a fundamental perspective of our work, the possibility of conceiving hydrocephalus and/or slit ventricle syndrome as phase transitions in the brain. This could be supported by the search for a symmetry connecting dilation and contraction and the corresponding spontaneous symmetry breaking mechanism. The idea of a phase transition is supported by the reciprocity of the inflated and collapsed ventricular states on one hand and the diverging susceptibilities associated with our instabilities on the other hand.
The main clues suggesting the signs of a phase transition are collected in Table 1. This table establishes clearly an analogy with the well-known paraelectric to ferroelectric state phase transition. The ferroelectric state which develops under a critical temperature Tc (the Curie temperature) is described by a non-zero spontaneous polarization P in keeping with the ordering of microscopic dipoles. The polarization is the associated order parameter of that transition. At the transition, the dielectric susceptibility follows the Curie–Weiss law δP/δE~1/(T − TC). This susceptibility connects the polarization to its “conjugated” field, the electric field E. All these fundamental ingredients have their counterparts in our approach. Indeed, the role of temperature being analogous to the conductance of the Sylvian aqueduct γ for the transport instability, and the ventricular area A for the elastic one, the corresponding susceptibilities scale as 1/(γ − γC) for the transport instability and as 1/keff ~1/(A − AC) for the elastic one. Both expressions follow the Curie–Weiss law and diverge at the “transition”. The collapsed and inflated ventricles correspond to two possible orientations of the polarization in a ferroelectric solid: polarization reversal costs additional energy. We thus expect a similar energy cost to reduce the ventricle size, explaining why no spontaneous return is possible.
Table 1.
Biophysical parameters compared do parameters of physical phase transitions
| Transport instability | Elastic instability | |
|---|---|---|
| Driving parameter | Aqueduct conductance γ | Ventricular area A |
| Critical parameter | Conductance threshold γC connected to secretion rate | Critical area AC connected to equilibrium area and biophysical parameters |
| Order parameter/conjugated ‘field’ | CSF pressure p / CSF flow through the aqueduct 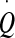
|
Ventricular volume V / CSF pressure p |
| Susceptibility | 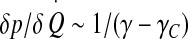 |
Compliance C = δV/δp~1/(A − AC) |
| Divergence at the transition | Yes | Yes |
In both cases, all parameters are analogous to the parameters driving the paraelectric–ferroelectric phase transition
The search for the formulation of our approach as a theory of phase transitions would be of great physical and clinical interest. Such a formulation can be reached through the identification of any “thermodynamic potential” of which the minima are the steady states of the ventricles. Identification of the symmetry “broken” at the transition would be of great help for the construction of this potential. This fundamental step is still in progress because of the complexity of our dynamical equations.
The clinical relevance of this formulation relies on the kinetics of the phase transition describing the time evolution of the state of the system, that is, the way CSF pressure, the area of the ventricles and their shape evolve with time. It would then allow for the prediction of the evolution of the condition.
The electrical interpretation of our equations is also an interesting and clinically relevant perspective. Indeed, Eq. 15 is the transfer function of a low pass filter which defines the simplest electrical analogue to be associated with “healthy” ventricles. Keeping this line of thought, we expect a more complex electrical interpretation of “sick” ventricles. The search for electrical analogues of intracranial dynamics is one of the most often encountered ways [9] to model ventricles and other intracranial compartments. Though not rigorously derived and rarely allowing for the identification of some causes of the intracranial pathologies, their intuitive content and their easier handling cannot be disputed. In our approach, these analogues can be rigorously derived from ventricular dynamics and the signature of the pathologies is a drastic change of the electrical analogues. But this is not the main interest of a predictive dynamical theory of hydrocephalus. It also allows us to understand and to model the possible issues of any curative strategy. For instance, the installation of a ventricular shunt [37] to restore normal conditions can be approached through our model. The external conduit evacuating excess CSF offer new pathways to CSF with additional conductances. If the pathological state originates from transport instability, the adjustment of the new conductance and its consequences on ventricular dynamics can be calculated (and its effects anticipated) rigorously.
Conclusion
Looking for a mechanism of the observed enlargement of hydrocephalic ventricles, we found a description of the ventricular wall dynamics pointing out fundamental causes which overlap several categories of hydrocephalus. A unified picture of hydrocephalus and slit ventricle syndrome as consequences of bifurcations of ventricular dynamics follows from our approach. More precisely, the expansion or contraction of brain ventricles are the clinical signatures of two bifurcations of their dynamics. The “elastic instability” results from a competition between the elastic properties of the ependyma and the interfacial tension of CSF in contact with the tissues. It is associated with a negative compliance. The “transport instability” arises from a competition between the ability of the aqueduct to evacuate CSF and its secretion by choroid plexus. Unlike the elastic instability case, the transport instability may either lead to a dilation of the ventricles, or their contraction. The remarkable dependence of the compliance on the ventricles’ shape factor raises the question of the influence of the shape of the ependyma on its dynamics. This problem remains to be solved but it is intimately connected to the formulation of the rigorous dynamics of the ventricles and their steady state. Viewing hydrocephalus as a “dynamical” condition of the intracranial system associated with structural instabilities of the brain ventricles yields two fundamental consequences. The usual distinction between communicating and non-communicating hydrocephalus is given a physical justification which should be of interest to physicians from a clinical point of view. But more fundamentally, the divergent susceptibilities associated with these bifurcations suggest an interpretation in terms of phase transitions of the intracranial system opening the way to new curative strategies.
References
- 1.Greitz D. Radiological assessment of hydrocephalus: new theories and implications for therapy. Neurosurg. Rev. 2004;27:145–165. doi: 10.1007/s10143-004-0326-9. [DOI] [PubMed] [Google Scholar]
- 2.Balédent, O., et al.: Relationship between cerebrospinal fluid and blood dynamics in healthy volunteers and patients with communicating hydrocephalus. Invest. Radiol. 39(1), (2004) [DOI] [PubMed]
- 3.Sweetman B, Linninger AA. Cerebrospinal fluid flow dynamics in the central nervous system. Ann. Biomed. Eng. 2011;39(1):484–496. doi: 10.1007/s10439-010-0141-0. [DOI] [PubMed] [Google Scholar]
- 4.Mori K. Current concept of hydrocephalus: evolution of new classifications. Child’s Nerv. Syst. 1995;11:523–532. doi: 10.1007/BF00822842. [DOI] [PubMed] [Google Scholar]
- 5.Fin L, Grebe R. Three dimensional modeling of the cerebrospinal fluid dynamics and brain interactions in the aqueduct of Sylvius. Comput. Methods Biomech. Biomed. Eng. 2003;6(3):163–170. doi: 10.1080/1025584031000097933. [DOI] [PubMed] [Google Scholar]
- 6.Milhorat TH. Experimental hydrocephalus. A technique for producing obstructive hydrocephalus in the monkey. J. Neurosurg. 1970;32:385–389. doi: 10.3171/jns.1970.32.4.0385. [DOI] [PubMed] [Google Scholar]
- 7.Hakim S, Adams RD. The special clinical problem of symptomatic hydrocephalus with normal cerebrospinal fluid pressure. J. Neurol. Sci. 1965;2:307–327. doi: 10.1016/0022-510X(65)90016-X. [DOI] [PubMed] [Google Scholar]
- 8.Hakim CA, Hakim R, Hakim S. Normal pressure hydrocephalus. Neurosurg. Clin. N. Am. 2001;36(4):761–772. [PubMed] [Google Scholar]
- 9.Marmarou A, Schulman K, LaMorgese J. Compartmental analysis of compliance and outflow resistance of cerebrospinal fluid system. J. Neurosurg. 1975;43:523–534. doi: 10.3171/jns.1975.43.5.0523. [DOI] [PubMed] [Google Scholar]
- 10.Ambarki K, et al. A new lumped-parameter model of craniospinal hydrodynamics during cardiac cycle in healthy volunteers. IEEE Trans. Biomed. Eng. 2007;54(3):483–491. doi: 10.1109/TBME.2006.890492. [DOI] [PubMed] [Google Scholar]
- 11.Wirth, B.: A mathematical model for hydrocephalus. M.Sc. Thesis, University of Oxford (2005)
- 12.Nagashima T, et al. Biomechanics of hydrocephalus: a new theoretical model. Neurosurgery. 1987;21(6):898–904. doi: 10.1227/00006123-198712000-00019. [DOI] [PubMed] [Google Scholar]
- 13.Drake JM, et al. Realistic simple mathematical model of brain biomechanics for computer simulation of hydrocephalus and other brain abnormalities. Can. J. Neurol. Sci. 1996;23:S5. [Google Scholar]
- 14.Tenti G, Sivaloganathan S, Drake JM.Brain biomechanics: Steady-state consolidation theory of hydrocephalus Math. Q. 199971111–124.16874690938.92005 [Google Scholar]
- 15.Bouzerar R, et al. Ventricular dilation as an instability of intracranial dynamics Phys. Rev. E 200572519122005PhRvE..72e1912B 10.1103/PhysRevE.72.051912 [DOI] [PubMed] [Google Scholar]
- 16.Takei F, Hirano A, Shapiro K, Kohn IJ. New ultrastructural changes of the ependyma in experimental hydrocephalus. Acta Neuropathol. 1987;73:400–402. doi: 10.1007/BF00688267. [DOI] [PubMed] [Google Scholar]
- 17.Milhorat TH.Choroid plexus and CSF production Science 19691661514–1516.1969Sci...166.1514M 10.1126/science.166.3912.1514 [DOI] [PubMed] [Google Scholar]
- 18.Helfrich W. Elastic properties of lipid bilayers: theory and possible experiments. Z. Naturforsch., C. 1973;28:693–703. doi: 10.1515/znc-1973-11-1209. [DOI] [PubMed] [Google Scholar]
- 19.Gennes PG. Wetting: statics and dynamics. Rev. Mod. Phys. 1985;57:3. [Google Scholar]
- 20.Landau, L.D., Lifshitz, E.M.: Theory of Elasticity. Courses of Theoretical Physics, vol. 7. Pergamon, Oxford (1970)
- 21.David F. Geometry and field theory of random surfaces and membranes. In: Nelson D, Piran T, Weinberg S, editors. Statistical Mechanics of Membranes and Surfaces. New York: World Scientific; 2004. [Google Scholar]
- 22.Willmore TJ. Riemannian Geometry. Oxford: Oxford Science; 1993. [Google Scholar]
- 23.Bryant R.A duality theorem for Willmore surfaces J. Differ. Geom. 19842023–53.0555.53002 [Google Scholar]
- 24.Jost J. Riemannian Geometry and Geometric Analysis. Berlin: Springer; 2002. [Google Scholar]
- 25.Landau, L.D., Lifshitz, E.M.: Fluid Mechanics. Courses of Theoretical Physics, vol. 7. Pergamon, Oxford (1982)
- 26.Griffith MD, et al. Pulsatile flow in stenotic geometries: flow behaviour and stability J. Fluid Mech. 2009622291–320.24815652009JFM...622..291G1165.76387 10.1017/S0022112008005338 [DOI] [Google Scholar]
- 27.Womersley JR. Method for the calculation of velocity, rate flow, and viscous drag in arteries when the pressure gradient is known. J. Physiol. 1955;127(3):553–563. doi: 10.1113/jphysiol.1955.sp005276. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Balédent O, et al. Brain hydrodynamics study by phase-contrast magnetic resonance imaging and transcranial color Doppler. J. Magn. Reson. Imaging. 2006;24(5):995–1004. doi: 10.1002/jmri.20722. [DOI] [PubMed] [Google Scholar]
- 29.Arfken G. Nonhomogeneous equation Green’s functions. In: Arfken G, editor. Mathematical Methods for Physicists. 3. Orlando: Academic; 1985. [Google Scholar]
- 30.Sourisse, A.: Propriétés spectrales de l’opérateur de Dirac avec un champ magnétique intense. Ph.D. Thesis, University of Nantes (2006)
- 31.Rekate HL. The slit ventricle syndrome: advances based on technology and understanding. Pediatr. Neurosurg. 2004;40:259–263. doi: 10.1159/000083737. [DOI] [PubMed] [Google Scholar]
- 32.Aimedieu P, Grebe R. Tensile strength of cranial pia mater: preliminary results. J. Neurosurg. 2004;100(1):11–114. doi: 10.3171/jns.2004.100.1.0111. [DOI] [PubMed] [Google Scholar]
- 33.Sorek S, Bear J, Karni Z. Resistances and compliances of a compartmental model of the cerebrovascular system. Ann. Biomed. Eng. 1989;17:1–12. doi: 10.1007/BF02364270. [DOI] [PubMed] [Google Scholar]
- 34.Kratochvíl A, Hrncír E. Correlations between the cerebrospinal fluid surface tension value and 1. Concentration of total proteins 2. Number of cell elements. Gen. Physiol. Biophys. 2002;21:47–53. [PubMed] [Google Scholar]
- 35.Czosnyka M, et al. Physiol. Meas. Cerebrospinal fluid dynamics. 2004;25(5):R51–76. doi: 10.1088/0967-3334/25/5/r01. [DOI] [PubMed] [Google Scholar]
- 36.Bergsneider M, et al. What we don’t (but should) know about hydrocephalus. J. Neurosurg. 2006;104:157–159. doi: 10.3171/jns.2006.104.1.157. [DOI] [PubMed] [Google Scholar]
- 37.Klein, O.: Hydrocéphalie. Mesure du débit de liquide cérébrospinal chez l’adulte hydrocéphale porteur d’une dérivation ventriculaire externe. Ph.D. Thesis, University of Nancy I (2009)