Leukocyte Rolling on P-Selectin: A Three-Dimensional Numerical Study of the Effect of Cytoplasmic Viscosity

Abstract

Rolling leukocytes deform and show a large area of contact with endothelium under physiological flow conditions. We studied the effect of cytoplasmic viscosity on leukocyte rolling using our three-dimensional numerical algorithm that treats leukocyte as a compound droplet in which the core phase (nucleus) and the shell phase (cytoplasm) are viscoelastic fluids. The algorithm includes the mechanical properties of the cell cortex by cortical tension and considers leukocyte microvilli that deform viscoelastically and form viscous tethers at supercritical force. Stochastic binding kinetics describes binding of adhesion molecules. The leukocyte cytoplasmic viscosity plays a critical role in leukocyte rolling on an adhesive substrate. High-viscosity cells are characterized by high mean rolling velocities, increased temporal fluctuations in the instantaneous velocity, and a high probability for detachment from the substrate. A decrease in the rolling velocity, drag, and torque with the formation of a large, flat contact area in low-viscosity cells leads to a dramatic decrease in the bond force and stable rolling. Using values of viscosity consistent with step aspiration studies of human neutrophils (5–30 Pa·s), our computational model predicts the velocities and shape changes of rolling leukocytes as observed in vitro and in vivo.

Introduction

In inflammation, leukocytes migrate from peripheral blood to extravascular sites of infection to destroy pathogens. Leukocyte rolling on activated endothelium is an important step in this process. Rolling interactions of leukocytes with vascular endothelial cells are mediated primarily by endothelial P-selectin that binds P-selectin glycoprotein ligand-1 (PSGL-1) expressed on the surface of leukocytes (1–4). In vitro studies with rigid bead cell-free systems (5,6) and adhesive dynamics simulations (7,8) demonstrated the importance of bond dynamics in cell rolling, whereas in vivo and in vitro experiments with neutrophils and monocytes (9–12) suggest that cell deformation may be responsible for stabilization of the mean rolling velocity of leukocytes at high shear stresses.

Realistic computational models of leukocyte rolling can bridge in vitro and in vivo assays and quantify differences in the leukocyte behavior between these assays and between humans and animals. Rigid cell models (7,13–16) are a good way to study the effect of receptor-ligand binding kinetics on cell rolling and adhesion at low, subphysiological shear stresses. However, under physiological conditions cell deformation becomes significant (11,17). Several groups have proposed to resolve this issue by modeling the leukocyte as a rigid cell with deformable microvilli (18–21). This may work at low shear stresses, but at physiological flow conditions, both leukocyte deformation and microvilli extension (22) contribute to the rolling process.

Available three-dimensional models of deformable leukocyte rolling and adhesion treat the cell as a liquid capsule in which the bulk of the cell has the same properties as the extracellular fluid, and cell deformation is controlled by the mechanical properties of its membrane or cortical layer (23,24) or as a compound liquid drop with cortical tension and bulk viscoelasticity of the nucleus and the cytoplasm (25,26). In leukocytes and other nucleated cells, the network of actin filaments is tightly connected to the networks of intermediate filaments and microtubules, producing an effective bulk viscosity much greater than the surrounding fluid. This difference in viscosity indicates that a liquid capsule model does not capture the key features of leukocytes (27).

Here, we examine the effect of cytoplasmic viscosity on P-selectin-mediated leukocyte adhesion and rolling in a parallel-plate flow chamber using a new version of our three-dimensional computational model for deformable cell adhesion. In this model, abbreviated as viscoelastic cell adhesion model (VECAM), both the cell and its microvilli were considered as viscoelastic materials and P-selectin/PSGL-1 binding was simulated using single-bond kinetics based on a probabilistic approach.

Methods

Model development

VECAM is a custom incompressible computational fluid dynamics solver in which the leukocyte shape is tracked by the volume-of-fluid/piecewise-linear interface calculation method and the force exerted on the cell membrane is determined by the continuous surface force method (26,28). The solver was written in FORTRAN and parallelized using OpenMP directives to run on shared-memory multiprocessor nodes of the Linux cluster at the Tulane Center for Computational Science (New Orleans, LA).

We modeled the leukocyte as a viscoelastic drop consisting of two compartments (phases): the nucleus (core) and the cytoplasm (shell) (Fig. 1 A). The plasma membrane and the actin cortex form a layer of infinitesimal thickness that possesses cortical tension (29). Cylindrical microvilli modeled as massless viscoelastic rods are distributed equidistantly over the cell membrane using spherical coordinates centered on the cell (7) and the cubature formulae (30). Cell adhesion molecules present on microvilli tips (i.e., PSGL-1) interact with their counterparts (P-selectin) distributed uniformly over the lower surface (substrate) of the rectangular flow channel if the separation distance between a microvillus tip and the substrate is less than or equal to the total length of interacting molecules l_r + l_l (Fig. 1 A). Receptor-ligand bonds respond elastically to external forces, generating a pulling force (bond force) on microvilli and the cell body. To determine this force, probabilistic single bond kinetics is used. The flow channel is characterized by length L, width W, and height H (Fig. 1 B). The pressure drop ΔP between the inlet and outlet of the channel leads to fully established flow of a Newtonian fluid (saline, growth medium, blood plasma, etc.) that exerts the hydrodynamic force on the leukocyte (Fig. 1 C). The motion and deformation of the leukocyte are the result of the balance between the hydrodynamic force, the bond force, the force due to cortical tension, the inertial force, and the net external force including gravity. More details about the VECAM and the input and output of the model are available in the Supporting Material and Table 1.

Figure 1.

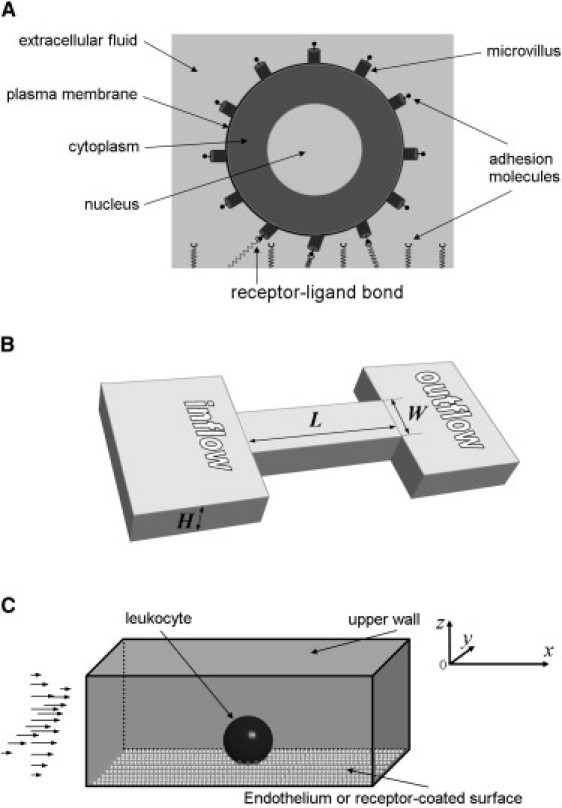
Sketch of the geometry used in the numerical simulation of leukocyte rolling. (A) The leukocyte is modeled as a compound viscoelastic drop of initially spherical shape consisting of the cell cytoplasm and nucleus. The plasma membrane is treated as a layer of infinitesimal thickness that possesses cortical tension. The cell has cylindrical microvilli with adhesion molecules (PSGL-1) on their tips. (B) The flow domain is a rectangular channel of length l, height h, and width w. The imposed boundary conditions reconstitute fully developed flow in a parallel-plate flow chamber or a rectangular microchannel. (C) The leukocyte is located sufficiently close to a P-selectin-coated substrate to form bonds between P-selectin and PSGL-1. The initial density of receptor-ligand bonds is zero. In the model, x axis coincides with the flow direction, z axis is perpendicular to the flow (from bottom to top); and y axis is perpendicular to the flow and parallel to the substrate. The origin is the left-front-bottom corner of the flow domain.

Table 1.

Values of model parameters

Parameter	Notation	Value	Reference
Cell radius	R	3.82 μm	(52)
Volume fraction of the nucleus	φ	25.9%	(52)
Cell density	ρc	1080 kg m−3	(72)
Cortical tension	Tc	0–300 μN m−1	(23,53,73)
Cytoplasmic viscosity	μcp	5–100 Pa s	(27,29,50–54)
Nuclear/cytoplasm viscosity	μn/μcp	1–10	(74)
Cytoplasmic relaxation time	λ1cp	0.176 s	(52)
Nuclear relaxation time	λ1n	0.200 s
Giesekus parameter for the cytoplasm and nucleus	κcp, κn	0
Surface density of receptor molecules (P-selectin)	nr	145 mol μm−2	(11)
Number of ligand molecules (PSGL-1) per microvillus	Nl(mv)	17	(3,75)
Receptor contour length	lr	40 nm	(76)
Ligand contour length	ll	45 nm	(77)
Unstressed bond length	lb0	70 nm	(21)
Forward reaction rate for unstressed bonds	kf0	1.70 μm2 s−1 mol−1	(78)
Reverse reaction rate for unstressed bonds	kr0	1 s−1	(79)
Bond bound state spring constant	κb	5.30 pN nm−1	(80)
Bond transition state spring constant	κts	0.10 pN nm−1	(81)
Temperature	T	310 K ≈ 37°C
Number of microvilli	Nmv	729	(44,82)
Microvillus tip radius	rmv	0.05 μm	(83)
Unstressed microvillus length	lmv0	0.50 μm	(82)
Microvillus spring constant	κmv	43.0 pN μm−1	(84)
Microvillus viscosity	μmv	30.1 pN s μm−1	(84)
Tether viscosity	μether	11.0 pN s μm−1	(84)
Critical force for tether formation	F0	61 pN	(84)
Force amplification factor	γ	8	(80)
Extracellular fluid density	ρext	1025 kg m−3
Extracellular fluid viscosity	μext	0.001 Pa s
Wall shear stress	τw	0.05 Pa (1 Pa = 10 dyn cm−2)
Channel length	L	60.0 μm
Channel width	W	2.50 cm
Channel height	H	500 μm

Results

Rolling velocity

For a constant fluid shear stress, an increase in the cell viscosity leads to larger variations of the instantaneous velocity (Fig. 2) and faster rolling (Fig. 3 A) and the detachment of the cell above the threshold viscosity (>300 P; see Fig. 2 and the Supporting Material). The mean rolling velocity of the leukocyte increases exponentially with the cytoplasmic viscosity: from 2.55 μm/s at the viscosity of 50 P to 21.2 μm/s at 1000 P (Fig. 3 A). Error bars in Fig. 3 A are an indicator of the jerkiness of the cell motion because the mean rolling velocity in this figure was calculated by averaging the instantaneous velocity data over the time period from the establishment of cell rolling (see the Supporting Material) to the end of the simulation and then over independent runs of the computational model.

Figure 2.

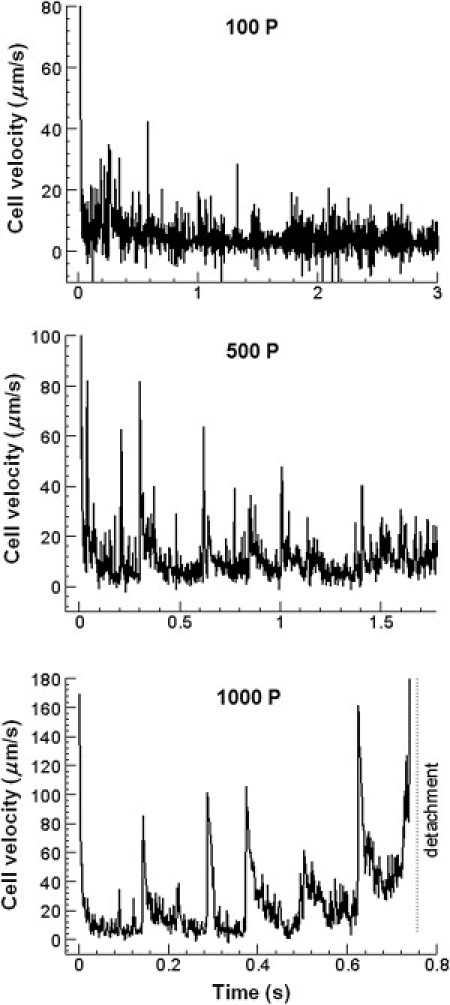
Instantaneous velocity of the leukocyte versus time for different values of the cytoplasmic viscosity. Significant temporal variations in the velocity leading to cell detachment are observed for high-viscosity cells.

Figure 3.

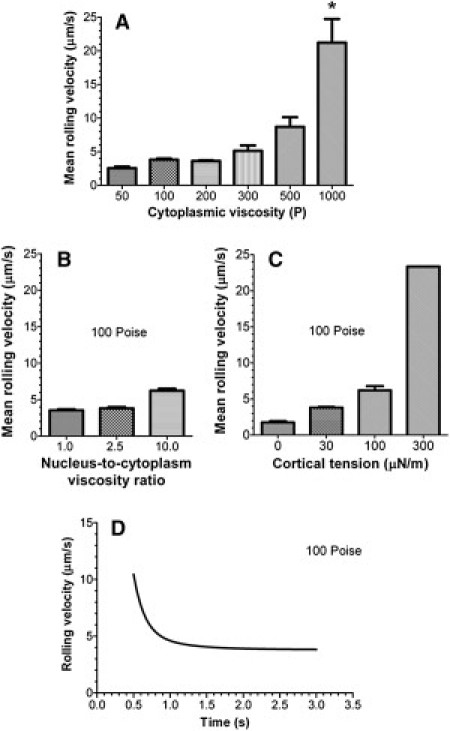
(A) Mean rolling velocity of the leukocyte as a function of the cytoplasmic viscosity. (^∗) In all runs, a 1000 P-viscosity cell detaches for the substrate within a simulation time of 1 s. (B) Effect of the nuclear viscosity on the mean rolling velocity. (C) Effect of the cortical tension on the mean rolling velocity. The cell continues to roll for a simulation time of 3 s even with a 10-fold increase in the cortical tension (from 30 to 300 μN m⁻¹). (D) Nonlinear regression fit of the rolling velocity versus time data to the two-phase decay model. In panels B–D, the cytoplasmic viscosity is 100 P.

The nuclear viscosity and cortical tension have a similar influence on the mean rolling velocity. A 10-fold increase in the nuclear/cytoplasm viscosity for the cell with cytoplasmic viscosity of 100 P almost doubles the cell velocity: from 3.54 μm/s at μ_n/μ_cp = 1 to 6.23 μm/s at μ_n/μ_cp = 10 (Fig. 3 B). The cortical tension effect is much stronger than the effect of nuclear viscosity and comparable with the effect of cytoplasmic viscosity: a 10-fold increase in cortical tension (from 30 to 300 μN m⁻¹) increases the mean velocity sixfold from 3.8 μm/s to 23.4 μm/s (Fig. 3 C). The main difference between the cortical tension and cytoplasmic viscosity effects is that the cell with a high cortical tension continues to roll on the substrate, whereas the cell with a high cytoplasmic viscosity (500 P and 1000 P) detaches from the substrate shortly after initial contact.

The time dependence of the rolling velocity is well described by a two-phase decay model: U_roll (t) = U_p + (U₀ − U_p)[α exp(−t/τ₁) + (1 − α) exp(−t/τ₂)], where subscripts “0” and “p” denote the initial (at t = 0) and plateau (at t → ∞) values of the velocity, τ₁ and τ₂ are time constants, and α is the coefficient between 0 and 1 that determines the relative contribution of the first phase (with τ₁) to the exponential decay. In Fig. 3 D, U_p = 3.81 μm/s, U₀ = 158 μm/s, τ₁ = 0.15 s (which is close to the relaxation time of the leukocyte cytoplasm), τ₂ = 0.52 s, and α = 0.97. Whereas the first time constant is associated with the solvent viscosity-driven expansion of the cell-substrate contact area, the second constant points to a much slower elongation of the cell driven by the polymer viscosity (see text about the apparent viscosity increase in the Supporting Material). This effect is similar to a rapid elastic rebound followed by viscous deformation of human neutrophils during the recovery test in a micropipette (31). For reference, a 4.5 μm-radius rigid sphere with 30,000 ligand molecules distributed over 6000 microvilli establishes steady-state rolling on a substrate with the receptor surface density of 1000 molecules μm⁻² at $t{\dot{\gamma }}_w\ge 5.0$, where ${\dot{\gamma }}_w$ is the wall shear rate (7). In our case, ${\dot{\gamma }}_w=50{\mathrm{s}}^{-1}$ and thus the corresponding time to reach steady state is ∼0.1 s for the cell of infinite viscosity, much less than that for a 100 P-viscosity cell.

Contact area and the number of bonds

As with the deformation index, the cell-substrate contact area decreases exponentially with the cytoplasmic viscosity: from 19.4 μm² at μ_cp = 100 P to 2.66 μm² at 1000 P (more than a sevenfold decrease; see Fig. 4 A and microvilli footprints animations in the Supporting Material). This indicates that a high-viscosity cell detaches from the substrate because it cannot form a sufficiently large contact area. The contact area also decreases with an increase in the nuclear viscosity or cortical tension: from 19.8 μm² at μ_n/μ_cp = 1 to 14.0 μm² at μ_n/μ_cp = 10 (Fig. 4 B) and from 19.4 μm² at T_c = 30 μN m⁻¹ to 8.27 μm² at T_c = 300 μN m⁻¹ (Fig. 4 C). Thus, cortical tension plays a less dominant role in deformation of rolling cells than the cytoplasmic viscosity, which explains why cells with a high cortical tension (300 μN m⁻¹) do not detach from the substrate.

Figure 4.

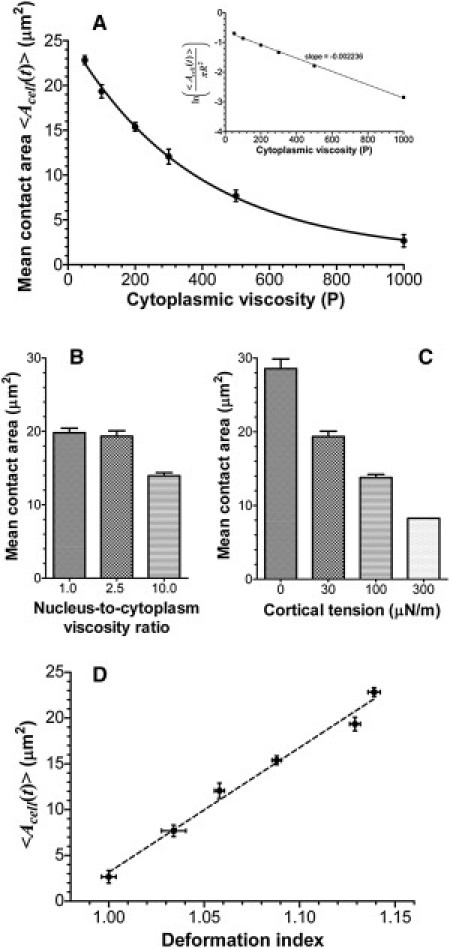
(A) Mean cell-substrate contact area as a function of the cytoplasmic viscosity. (Insets in A) The natural logarithm of the normalized mean contact area versus the cytoplasmic viscosity that illustrates a clean exponential relationship between the contact area and the viscosity. (B) Effect of the nuclear viscosity on the mean contact area. (C) Effect of the cortical tension on the mean contact area. (D) Mean contact area versus the deformation index of the cell.

Based on the linear relation between the contact area and the deformation index (Fig. 4 D), changes in the contact area of a rolling cell can be estimated from the measurement of the cell deformation index. A small increase in D_cell from 1.0 to 1.1, which is barely detectable from top- or bottom-view images of rolling cells, increases the contact area from 3 μm² to 15 μm². Therefore, the rolling cells that seemingly show no deformation in parallel-plate or microfluidic-flow-chamber experiments may have a large contact area and thus a large number of receptor-ligand bonds.

Receptor-ligand bonds between a rolling cell and the substrate can be divided between unstressed bonds that are located closer to the center of the cell-substrate contact region and exert no force on the cell body and stressed or load-bearing bonds at the periphery of the contact region that contribute to the bond force. There is an exponential decrease in the total number of bonds with the cell viscosity (Fig. 5 A) and thus a positive correlation between the total number of bonds, contact area, and deformation index. However, the number of load-bearing bonds is insensitive to the cell viscosity for values >200 P (or a deformation index <1.12) (Fig. 5 B). If a 50 P-viscosity cell has, on average, 16 load-bearing bonds, 200 P and higher viscosity cells have approximately nine bonds. Thus, a cell can roll with a small number of load-bearing bonds, but a significant amount of unstressed bonds are needed to quickly replenish the population of load-bearing bonds after bond rupture events.

Figure 5.

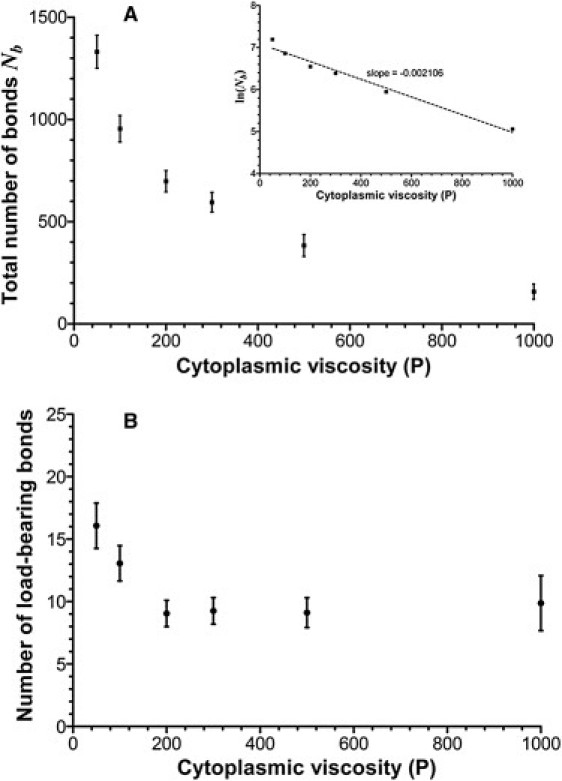
(A) Total number of receptor-ligand bonds and (B) number of load-bearing (stressed) bonds as a function of the cytoplasmic viscosity of a rolling cell. (Insets in A) The natural logarithm of the total number of bonds versus the cytoplasmic viscosity that shows a clean exponential relationship between the total number of bonds and the viscosity. The viscosity has a small effect on the number of load-bearing bonds, but it dramatically decreases the number of unstressed bonds.

The distribution of loads on microvilli in the contact region (see animations in the Supporting Material) indicate that most load-bearing bonds are located at the periphery of the cell (far from the midplane y = y_c, where y_c is the y coordinate of the cell centroid). This shows the necessity of using fully three-dimensional models for realistic simulation of leukocyte rolling and adhesion.

Hydrodynamic and bond forces

To further understand why leukocyte rolling requires a large contact area, we analyzed the forces acting on a rolling cell. Hydrodynamic and bond forces are much larger than forces arising from gravity, cortical tension, and inertia (H. Lan and D. B. Khismatullin, unpublished). The magnitude of the bond force (F_bx and F_bz; solid squares in Fig. 6) drops with time until a plateau is reached. This plateau continues indefinitely for a stably rolling cell but if the cell detaches, the bond force drops to zero (see the 1000 P case in Fig. 6). Similarly, the drag force (F_drag) (left panel in Fig. 6) and the lift force (F_lift) (right panel) decrease with time. Immediately after forming the first bonds, F_drag ≈ −F_bx ≈ 80 pN and F_lift ≈ −F_by ≈ 200 pN and these values do not change with the cytoplasmic viscosity. For more deformable cells, a decrease in the bond force with time is more pronounced. For a 200 P-viscosity cell, the plateau values of |F_bx| and |F_bz| are 5 pN and 92 pN, respectively (Fig. 6, top). Thus, before this cell establishes stable rolling, the x component of the bond force drops by 75 pN and the y-component decreases by 108 pN. For a 1000 P-viscosity cell, a change in the bond force from its tethering value to the value before detachment is very small: 16 pN for the x component and 20 pN for the y-component (Fig. 6, bottom).

Figure 6.

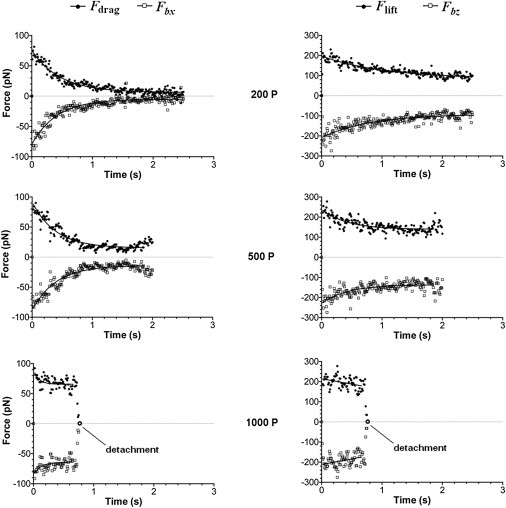
Bond and hydrodynamic forces on a rolling cell as a function of time for different values of the cytoplasmic viscosity. (Left panel) Drag force (upper curve, solid circles) and the translational (x-) component of the bond force (lower curve, open squares). (Right panel) Lift force (upper curve, solid circles) and the normal (z-) component of the bond force (lower curve, open squares). The bond force drops to zero (open circle) and the drag and lift forces decrease to very small values when the cell detaches.

The bond force for low-viscosity cells drops because of a decrease in the mean length of load-bearing bonds 〈Δl_b〉. This effect is not associated with changes in the mean number of load-bearing bonds 〈N_lbb〉 because cells with cytoplasmic viscosity between 200 P and 1000 P have approximately nine load-bearing bonds (Fig. 5 B). Ignoring the y component of the bond force (<1 pN for all cases considered), we can estimate this length from the mean bond force data as follows (see Eq. S6 in the Supporting Material):

$$\langle \Delta l_b\rangle =\frac{1}{\gamma {\kappa }_b\langle N_{lbb}\rangle }\sqrt{F_{bx}^2+F_{bz}^2}.$$ (1)

For γ = 8, κ_b = 5.3 pN nm⁻¹, and the data in Fig. 6, the mean bond length from Eq. 1 is 0.5 nm for a 1000 P-viscosity cell before detachment, whereas it is 0.24 nm for a 200 P-viscosity cell during its stable rolling. Due to the increased rotational speed of the higher viscosity cell, bonds at the trailing edge of the cell are highly extended before their rupture. Likewise, because the drag torque on a deformable cell with a large, flat contact area is much less than the drag torque on a rigid sphere (26), the rotational speed of this cell is low. As a result, bonds are less extended before rupture and oriented almost parallel to the z axis.

Unlike a rigid sphere near the wall for which the lift predicted by the Goldman-Cox-Brenner theory (32) is zero, rolling cells experience the lift force due to the lubrication pressure in the gap between the cell and the substrate. The bond force leads to much higher values of the lift force (right panel of Fig. 6) because of a dramatic increase in the lubrication pressure, as discussed by Hodges and Jensen (33). This is especially true when the average orientation angle of load-bearing bonds approaches 90° for stably rolling cells (see above).

Discussion

The ability of leukocytes to deform is essential for both homeostasis and immune responses. When circulating in blood, these nucleated cells with a diameter of 7–10 μm (34,35) need to deform to pass through the smallest blood vessels such as true capillaries (5–9 μm). Tissue perfusion is compromised when the deformability of circulating leukocytes is reduced below normal values (36). The presence of a large number of stiff leukocytes in blood due to their untimely activation is a feature of sepsis and posttraumatic shock, acute and ventilator-induced lung injury, ischemia-reperfusion injury, and many other pathological conditions (see the review by Khismatullin (27)). In larger vessels such as postcapillary or small collecting venules, leukocytes come in contact with vascular endothelial cells, where they first roll on and then are firmly attached to the endothelium. When rolling, leukocytes begin to be activated through signaling induced by chemoattractants present on the surface of endothelial cells (27). The transition to the active state completes during firm adhesion (arrest) and the activated leukocytes migrate across the endothelium and subsequently in the interstitial tissue to reach pathogens (37).

Our numerical study shows that the cytoplasmic viscosity, which is a key determinant of leukocyte deformability, plays a critical role in the ability of leukocytes to roll on the adhesive substrate. Thus, to establish rolling, the viscosity of the cells should be less than a threshold value. Below this value, a decrease in the cytoplasmic viscosity leads to an exponential increase in the area of contact of a rolling cell with the substrate. This in turn increases the number of unstressed receptor-ligand bonds. Although the number of load-bearing bonds remains low independent of the viscosity value, cell rolling requires a large population of unstressed bonds in the cell-substrate contact region to quickly replenish load-bearing bonds after bond rupture events and rotation of the cell. Thus, one of the reasons why a high-viscosity cell detaches from the substrate is because the rate of formation of unstressed bonds in this cell is insufficient to keep a large stock of unstressed bonds in the contact region. With the rate of bond formation less than the rate of bond rupture, the number of unstressed bonds and the contact area will decrease with time until the cell detaches.

This result suggests the following mechanism for leukocyte-endothelial cell adhesion. During initial contact with endothelial cells and early rolling, passive leukocytes deform substantially and form a large area of contact with the substrate to stabilize rolling and sample the endothelium for signals. Signaling leads to conformational change of β₂ integrins in the cell-substrate contact region to a high-affinity state (38–42) and to cytoskeleton remodeling that in turn increases the cytoplasmic viscosity (27,43). Some of these signals may also lead to disassembly of leukocyte microvilli (44) or the microvillus length may decrease because of the extension of the cell surface in the contact region, thereby exposing high-affinity β₂ integrins located in space between microvilli (45) to their ligands on the endothelium. All these eventually lead to firm adhesion of the leukocyte. (Note that the formation of a large contact area coupled with leukocyte stiffening due to activation reduces the possibility for the hydrodynamic force to decrease the contact area and detach the cell.)

Three lines of experimental evidence indicate that the cell deformability significantly influences the cell rolling process. These include: 1), cell deformation-induced stabilization of the rolling velocity at high shear stresses (9–12); 2), reduction of the rolling velocity with leukocyte treatment with cytochalasins (fungal metabolites that disrupt actin cytoskeleton and thus make the cells more deformable (46,47)); and 3), higher rolling velocities for less deformable glutaraldehyde-fixed leukocytes (48) (i.e., the inverse to number 2). It is important to mention differences in rolling between rigid beads and live cells. Detachment assays with sPSGL-1- and 2-GSP-6-coated beads (200 sites μm⁻²) (11) demonstrate no rolling of the beads on P-selectin if the wall shear stress is >3 dyn cm⁻² at a P-selectin density of 145 sites μm⁻² or 4 dyn cm⁻² at 486 sites μm⁻². On the contrary, the same study shows that human neutrophils roll on P-selectin with a velocity <10 μm s⁻¹ at shear stresses as high as 32 dyn cm⁻² (compare Figs. 3 and 4 B in Yago et al. (11)). Leukocytes and bead models of cells differ in key ways. Leukocytes are viscoelastic, and have microvilli and 80% of ligand (PSGL-1) molecules are clustered on the microvilli tips (49) that can extend when the force exceeds a critical value, whereas rigid beads used in rolling experiments had no structures similar to microvilli and no ligand clusters. Our numerical results indicate the observed differences in rolling and adhesion between these two systems are primarily due to differences in their mechanical properties.

In our numerical algorithm, the leukocyte is modeled as a viscoelastic drop with cortical tension. This type of leukocyte model was extensively used in micropipette aspiration studies (29,50–54) to measure rheological properties of human neutrophils and other leukocytes. Here, cell deformability is determined by bulk viscoelasticity (e.g., cytoplasmic and nuclear viscosities) and surface elasticity (cortical tension). Our results show that an increase in any of these parameters reduces the cell-substrate contact area and increases the mean rolling velocity. However, the cytoplasmic viscosity plays a more dominant role in leukocyte deformation and the ability of this cell to roll on the substrate. Our explanation of why bulk mechanical properties of live cells are critically important in cell deformation is as follows. Leukocytes are nucleated cells with a rich network of vimentin filaments and microtubules connecting the plasma membrane to the cell nucleus (27). The networks of these filaments are the major source of bulk viscoelasticity of the cell. Cortical tension results from the actin cytoskeleton in the cell cortex, a thin layer beneath the plasma membrane, provided it is not connected to the three-dimensional networks of intermediate filaments (such as vimentin) and microtubules. The latter assumption is invalid for most nucleated cells, including leukocytes based on experimental evidence of direct linkage between actin filaments, intermediate filaments, and microtubules (55–58). Thus, remodeling of actin cytoskeleton leads to changes in the network structure of intermediate filaments and microtubules (55,59), thereby changing bulk mechanical properties of the cell. Additional evidence comes from micropipette aspiration experiments, which show a large variability of the measured values of the cytoplasmic viscosity (51–53) but a relatively robust measurement of cortical tension (53,60). This indicates that cytoskeleton remodeling due to cell activation during aspiration (61) primarily influences the cytoplasmic viscosity but not the cortical tension.

Tight interactions between actin filaments, vimentin filaments, and microtubules indicate that the correct description of leukocyte biomechanics requires fully three-dimensional computational models that take into account both bulk and surface mechanical properties of the cell. VECAM is, to our knowledge, the first algorithm of this kind, where the constitutive model tested in micropipette aspiration studies has been used. In the capsule models, the bulk properties were not considered and, as a result, such models predict the deformation of rolling leukocytes with the value of cortical tension increased by at least one order of magnitude from its measured value (23,24). Our data in Figs. 5 and 6 show that it is possible to get similar rolling velocities and deformation of the cell in numerical simulations by considering low cytoplasmic viscosity and high cortical tension or high cytoplasmic viscosity and low cortical tension, provided the viscosity is below the threshold value for cell rolling. Bulk mechanical properties were considered in several two-dimensional models of cell rolling (46,62). Our previous report (26) and the data presented in this article (see microvilli footprints animations in the Supporting Material) indicate that receptor-ligand bonds on peripheral microvilli (far from the midplane of the cell) contribute substantially to the total bond force. Therefore, the usage of two-dimensional models for analysis of cell rolling or adhesion data is questionable. The novelty of the presented algorithm as compared to what we developed before (25,26) is that VECAM can simulate rolling of deformable cells using stochastic receptor-ligand binding kinetics, whereas the previous version was based on deterministic kinetics and applied only to the problem of leukocyte detachment at high shear stresses.

The elongation in the flow direction and the formation of a large, flat contact area in a low-viscosity cell changes the velocity field and the distribution of shear stresses on the cell surface. This leads to a decrease in the bond and hydrodynamic (drag and lift) forces with time until the cell reaches quasi-steady-state rolling. As seen in Fig. 6, a decrease in these forces with time becomes less pronounced with an increase in the cytoplasmic viscosity. Thus, a higher-viscosity cell has more extended bonds and, as follows from the force balance, experiences a stronger force from the flow. Because the bond lifetime decreases with bond extension and a decrease in the number of load-bearing bonds increases the z component of the cell velocity, such a cell has a higher probability to detach from the substrate. The increased frequency of bond rupture events in a higher-viscosity cell explains why the mean value of the rolling velocity and the amplitude of its time fluctuations increase with cytoplasmic viscosity. Thus, a less deformable cell will experience a more erratic motion (see error bars in Fig. 3 A), or vice versa, a more deformable cell will have more stable rolling. Overall, this result favors the hypothesis that stable rolling of leukocytes in vivo, with the plateau of the rolling velocity at high shear stresses, is attributable to leukocyte deformability (9–12).

The lift force influences the rolling and adhesion of deformable cells. According to hydrodynamic theory, if fluid inertia is insignificant, a spherical neutrally buoyant particle near a wall experiences a very small lift force due to shear flow. The asymptotic analysis (63,64) deduces that this force becomes even smaller for drops of low viscosity (1 cP) and bubbles. Several recent studies (65,66) on nonspecific adhesion of lipid vesicles, show, however, that a lift force arises if the vesicles are tilted due to the “fore-aft asymmetric pressure field beneath the vesicle” (65). Specific binding provides a much higher pulling force on the cell and results in significant disturbances of the velocity and pressure field around the cell. As seen in Fig. 6, the higher the normal (z-) component of the bond force, the higher the lift force.

We predict from comparison of the numerical and experimental data (see the Supporting Material) that the cytoplasmic viscosity of normal leukocytes ranges between 5 and 30 Pa s (50 and 300 poise). This is consistent with step aspiration studies of human neutrophils (52,67), where the cell viscosity was determined by using a standard viscoelastic solid model. The Giesekus equation used in our work includes most terms of this model. In addition, the value for the relaxation time in the simulation (λ_1cp = 0.176 s) is based on the data reported in those studies (λ_1cp is the same as μ/k₂ in the work of Schmid-Schonbein (34)). Thus, our computational model was able to reproduce the shape changes and velocities of rolling leukocytes at the values of the viscosity and relaxation time of the cell cytoplasm corresponding to the small-strain micropipette aspiration studies.

Future experimental studies will examine the effect of cytoplasmic viscosity on leukocyte rolling and adhesion. The use of receptor-coated microbeads can be extended to spherical particles with different internal viscosities. The use of such a deformable cell-free system provides more control over the bulk viscosity. The intracellular viscosity can be altered using low levels of agents that disrupt the cell cytoskeleton (e.g., cytochalasins or latrunculin). This approach is similar to what was done by Sheikh and Nash (47). Use of siRNA should provide a more targeted approach to regulate actin polymerization and cross-linking.

Leukocyte rolling in vivo is a complex dynamic process and there are additional factors involved, such as hydrodynamic interactions between erythrocytes and leukocytes (68), multiple receptor-mediated adhesion (69), catch bonds (70,71), and high-affinity integrin conformation (42). Although these issues will be addressed in future studies, the work presented in this article shows the interaction between fluid forces and cell deformation to promote adhesion and the range of likely viscosities that leukocytes exhibit.