Self-Organized Cell Motility from Motor-Filament Interactions

Abstract

Cell motility is driven primarily by the dynamics of the cell cytoskeleton, a system of filamentous proteins and molecular motors. It has been proposed that cell motility is a self-organized process, that is, local short-range interactions determine much of the dynamics that are required for the whole-cell organization that leads to polarization and directional motion. Here we present a mesoscopic mean-field description of filaments, motors, and cell boundaries. This description gives rise to a dynamical system that exhibits multiple self-organized states. We discuss several qualitative aspects of the asymptotic states and compare them with those of living cells.

Introduction

Cell migration is critical for many biological processes, including immune response, wound-healing, and embryonic development. Migration depends on the cytoskeleton, a dynamic network of filamentous proteins and molecular motors that provide the mechanical integrity and active force required for cell movement (1). The bulk of the cytoskeleton is composed of actin filaments. These filaments are assembled from asymmetric actin monomers that are oriented the same way, defining an orientation for the entire filament. Typically, one end of an actin filament (the barbed end) polymerizes, and the other (the pointed end) depolymerizes, leading to effective translation of the filament in a process known as treadmilling. Another major component of the cytoskeleton is myosin, a motor protein that binds to actin filaments. Upon hydrolysis of ATP, myosin changes its conformation, such that complexes of myosin can move actin filaments with respect to each other (2).

Investigators have found experimentally that actin polymerizes at the leading edge of the cell. This is the generally accepted mechanism for protrusion and advancement of the cell's front edge (3). Additionally, it was shown that myosin is important for cell polarization and motility (4–6). It was proposed that myosin-mediated contractility of actin is responsible for retraction of the trailing edge of the cell (7,8).

It is increasingly recognized that cell motility can be a self-organized process, in that the large-scale patterns of cytoskeletal structure, including a cell's ability to polarize globally, may arise from simple, local interactions of molecular constituents (9–12). For example, it was observed that fragments from a single fish keratocyte can move persistently, assuming the shape of an entire, intact keratocyte cell, which suggests that cell motion is not directed by a single “organizing center” (13). How local interactions give rise to cell polarization and motility is poorly understood. Although experiments have been essential in determining the cytoskeletal components and interactions involved in cell movement, physical models may be more useful for exploring the minimal requirements for self-organized motility.

Several models of cell motility have been developed. In some of these models, cell polarity is externally imposed and does not arise naturally from small-scale mesoscopic interactions. Although these models have biological relevance (e.g., in describing cells moving toward a chemical attractant), they do not address the requirements for self-organized motility (14–18). In other models, cell polarity arises naturally (e.g., from instabilities in the dynamics of signaling networks that regulate actin polymerization (19), or in the mechanical interactions of membranes and cytoskeletal constituents (20–22)). However, these models do not explicitly describe the dynamics of molecular motor redistribution during the course of polarization. Thus, the corresponding model predictions may not easily be compared with relevant experimental data on the cytoskeletal dynamics that accompany cell polarization. A recent model of cell motility (23) explicitly accounted for the dynamics of molecular motors, but other aspects of the description were largely phenomenological. In particular, boundary conditions at the cell edge did not explicitly follow from a microscopic description of the dynamics of the cytoskeletal filaments. Mesoscopic descriptions exploring self-organized behaviors in purified actomyosin networks have been published, but it is unclear how these descriptions apply to cells (24–26). In this work, we extend the mesoscopic mean-field models of actomyosin networks by coupling these networks to membranes, and explore the emergent behaviors of such systems.

Materials and Methods

We describe a system of polar treadmilling filaments, motor proteins, and a movable, closed boundary. The filaments and motors are confined to the region inside the boundary; we term this region the “cell” (Fig. 1). Filaments and motor proteins are described by their respective densities c and m. The dynamics of these densities are determined by the continuity equations

$$\begin{array}{l}{\partial }_{t}c\left(\mathbf{r},\theta ,t\right)=D{\nabla }^{2}c-\nabla ·\mathit{J}+\nu \left(\mathbf{r}\right)-{\nu }_{d}c,\hfill \\ {\partial }_{t}m\left(\mathbf{r},t\right)=D_m{\nabla }^{2}m-\nabla ·{\mathit{J}}_m.\hfill \end{array}$$ (1)

Here $c\left(\mathbf{r},\theta ,t\right)$ is the density of filaments with center of mass r, oriented along θ, and m is the density of molecular motors. Filaments are assumed to nucleate at a constant rate ν₀ only within the boundary, denoted by the function $\nu \left(\mathbf{r}\right)$, and degrade at a constant rate ${\nu }_d$. D and D_m are diffusion coefficients that capture the effect of random fluctuations. The filament current J consists of three contributions:

$$\mathit{J}={\mathit{j}}_t+{\mathit{j}}_a+{\mathit{j}}_B,$$ (2)

where j_t describes treadmilling dynamics, j_a describes molecular-motor-mediated filament interactions, and j_B captures the effects of confining boundaries as specified below. For simplicity, we assume all filaments to be of length ℓ. This is justified provided that a newly nucleated filament reaches some terminal length on a timescale much shorter than the timescale of the evolution of the density fields (27). Subsequently, subunits are added at the growing end of the filament at the same rate as they are removed from the shrinking end, leading to translation of the filament with effective speed υ; thus

$${\mathit{j}}_t\left(\mathbf{r},\theta \right)=\upsilon \hat{\mathbf{u}}c,$$ (3)

where $\hat{\mathbf{u}}=\left(\text{cos}\theta ,\text{sin}\theta \right)$ is a unit vector along θ. The active current ${\mathit{j}}_a$ captures the effects of motor mediated interfilament interactions (28,29). Explicitly,

$${\mathit{j}}_a\left(\mathbf{r},\theta \right)=\int d{\mathbf{r}}^{\prime }d{\theta }^{\prime }\alpha \left(\theta ,{\theta }^{\prime }\right)\mathit{f}\left({\mathbf{r}}^{\prime }-\mathbf{r}\right)\times \left(m_o\left({\mathbf{r}}^{\prime },{\theta }^{\prime }\right)c\left(\mathbf{r},\theta \right)+c\left({\mathbf{r}}^{\prime },{\theta }^{\prime }\right)m_o\left(\mathbf{r},\theta \right)\right).$$ (4)

Here $m_o\left(\mathbf{r},\theta \right)$ is the density of motors bound to filaments with center of mass r and orientation θ. It is assumed that locally, motors switch quickly enough among filaments such that the distribution of motors bound to filaments of different orientations will always be at equilibrium and therefore proportional to the angular filament density distribution: $m_o\left(\mathbf{r},\theta \right)=m\left(\mathbf{r}\right)c\left(\mathbf{r},\theta \right)/\int d{\theta }^{\prime }c\left(\mathbf{r},{\theta }^{\prime }\right)$. This assumption is valid provided that motors do not travel very far after unbinding from a filament and before rebinding to another. The function $\alpha \left(\theta ,{\theta }^{\prime }\right)\mathit{f}\left({\mathbf{r}}^{\prime }-\mathbf{r}\right)$ is the velocity of a filament at ${\mathbf{r}}^{\prime }$ due to interactions, via a motor, with a filament at r. Here, $\alpha =a\eta$, where a is interpreted as the strength with which myosin pulls on a pair of filaments, and η is the effective filament mobility. In experimental systems, changes in α could correspond to any changes in myosin activity, for example, due to the phosphorylation state of myosin. The proportionality between the velocity of a filament and the active force applied to it is derived from force balance equations applied to a single filament in the low Reynolds number limit, in which active forces are exactly canceled by viscous forces from the ambient fluid. The expressions for the currents of the density fields follow from the equations of motion for single filaments using a mean-field approximation; overall force balance is therefore naturally satisfied. For center-of-mass attractive interactions between filaments, we put

$$\mathit{f}\left({\mathbf{r}}^{\prime }-\mathbf{r}\right)=\frac{{\mathbf{r}}^{\prime }-\mathbf{r}}{\left|{\mathbf{r}}^{\prime }-\mathbf{r}\right|}\Theta \left(\ell -\left|{\mathbf{r}}^{\prime }-\mathbf{r}\right|\right),$$ (5)

where filament length ℓ serves as a cutoff for the range of attractive interactions, and Θ is the Heaviside function. This choice of f naturally ensures that the total active force in the system is zero. The parameter $\alpha \left(\theta ,{\theta }^{\prime }\right)$ encodes the magnitude of the interaction between a motor-filament pair and has units of velocity. The local velocity of filaments resulting from interfilament attractive forces is $\mathit{\varphi }\equiv \left({\mathit{j}}_a+{\mathit{j}}_B\right)/c$. Motors are assumed to move with the filaments to which they are attached. Thus the velocity of a motor at a point is given by the average filament velocity at that point:

$${\mathit{J}}_m\left(\mathbf{r}\right)=m\left(\mathbf{r}\right)\frac{\int d\theta \mathit{\varphi }\left(\mathbf{r},\theta \right)c\left(\mathbf{r},\theta \right)}{\int d\theta c\left(\mathbf{r},\theta \right)}.$$ (6)

Filaments are confined to an evolving domain whose boundary Γ evolves according to

$$\dot{\Gamma }=\zeta \mathit{f},$$ (7)

where ζ denotes an effective mobility determined by the Stokesian drag from the ambient fluid. The force density on the boundary $\mathit{f}=-\delta \left(\mathcal{F}+{\mathcal{F}}_I\right)/\delta \Gamma$ is determined from the Helfrich free energy $\mathcal{F}=\sigma L+\kappa \int d\Gamma H^2+P{\left(A-A_0\right)}^2$ and from the filament-boundary interaction term ${\mathcal{F}}_I=\int d\mathbf{r}d\theta c\left(\mathbf{r},\theta \right)V\left(\Gamma ,\mathbf{r}\right)$, where σ is surface tension, κ is the bending modulus, L is the length of Γ, H is the local mean curvature, A is the area of the domain constrained to remain approximately equal to A₀ for large values of P, and the function V describes a repulsive potential between filaments and Γ (30). According to Newton's third law, the boundary and filaments exert equal and opposite forces on each other, hence

$${\mathit{j}}_B=-\eta {\nabla }_{\mathbf{r}}V\left(\Gamma ,\mathbf{r}\right)c\left(\mathbf{r},\theta \right).$$ (8)

We explicitly show that the above expression for filament-boundary interactions conforms to force balance in Appendix A.

Figure 1.

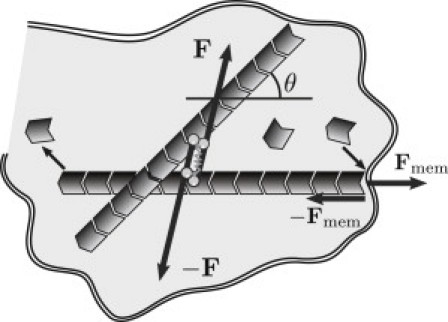
Cartoon of molecular processes described by our model. Polar filaments oriented along θ add subunits at one end and subtract subunits from the other end in the process of treadmilling. Consequently, the filaments push against the membrane, exerting force $F_{\text{mem}}$ on it while experiencing the opposite force from the membrane. Motors attached to filaments generate force dipoles applied to filament pairs.

Note that this description of the boundary neglects nonlocal hydrodynamic interactions. This simplifying assumption is admissible when the motion of the membrane in the vicinity of a substrate surface, where adhesive, friction-like forces are dominant, is being described (20,31). Details of the boundary-filament interactions are provided in Appendix A. Further comments on model assumptions and boundary treatments are included in the Supporting Material. Equations 1–8 fully specify the time evolution of the system. Of importance, Eqs. 1–8 conform to local force balance. In particular, filament-substrate interactions are captured by an effective friction, such that the force on a filament from the substrate cancels the force on the substrate due to that filament. Likewise, the total force on a filament pair due to motors, as well as the sum of forces acting between filaments and the boundary, vanishes.

Results and Discussion

Analysis of the two-dimensional model

In this section, we present numerical solutions to Eqs. 1–8. The details of the integration scheme are outlined in Appendix B. We find that the system exhibits two asymptotic states. In the stationary state, the boundaries and density profiles remain constant over time. The total filament density is rotationally symmetric and relatively flat throughout the cell, although with some accumulation near the boundaries. This accumulation is due to the arrest of filament treadmilling by the confining boundary potential. The motor densities are slightly elevated at the center, but fairly evenly distributed throughout the cell. In the moving state, boundaries and density profiles translate at a constant velocity (Fig. 2). The cell lacks rotational symmetry, but has reflection symmetry about an axis parallel to its direction of translation. In this case, motor and filament densities are peaked at the back of the cell. At the front of moving cells, the motor density is vanishingly small, whereas the filament distribution is flat, with accumulation near the boundaries, again due to treadmilling. Filament velocities are shown in Fig. 2 b; forward filament velocities are larger at the back of the cell due to the presence of motors.

Figure 2.

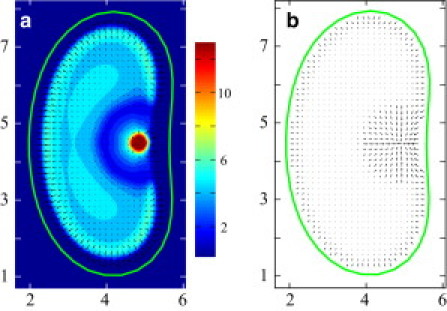
Moving-state solution to Eqs. 1–8. The cell moves to the left. The boundary is indicated by the green solid line. Parameters: $D=D_m=0.1{\ell }^2{\nu }_d,\alpha =2.5\ell {\nu }_d,\upsilon =1\ell {\nu }_d,\eta =0.02\zeta ,\sigma =15{\nu }_d\ell /\zeta ,\kappa =94{\nu }_d{\ell }^3/\zeta ,P=200{\nu }_d/\zeta$ and $A_0=20{\ell }^2$. As noted in Appendix B and the Supporting Material, we choose nondimensional scaling such that ${\nu }_d=1$, $\ell =1$, and $\zeta =1$. (a) The average density of filaments is represented by the heat map. The average polarization of filaments is indicated by arrows. (b) Average local velocity fields of filaments. Filament velocities are larger at the back of the cell due to the presence of motors. (Color online.)

Aggregation of motors is essential for the cell to commit to an asymmetric, moving state. Orientation-independent filament nucleation and degradation result in equal populations of filaments treadmilling in each direction. In the absence of motors, this drives the cell into a symmetric, stationary state. When interfilament interactions are weak, motors are diffuse, and local attractive forces are approximately uniform throughout the cell; therefore, they are not enough to destabilize the stationary state. However, when interfilament interactions are too large to be counteracted by treadmilling and turnover, motors and filaments become aggregated. If the initial filament and motor distributions are not exactly radially symmetric, this heterogeneity exerts an asymmetric force on the surrounding boundary, leading to an asymmetric state of the cell.

The system's transition between stationary and moving states is presented in a phase diagram (Fig. 3 a), determined as a function of the treadmilling speed υ and the interaction strength α, taken to be isotropic for simplicity. Below some critical value of α, moving states of the cell do not exist. Above some other critical value of α, only moving states exist. Between these two critical values, solutions to the system are bistable between moving and stationary states. Treadmilling appears to counteract the effects of attractive interactions in that larger values of α are needed for moving states to emerge when υ is increased. An intuitive explanation for this phenomenon is as follows: When treadmilling speed increases, filaments of different orientations move away from each other; to aggregate them, the attractive interaction must also be increased. For very large values of α and υ, the back and front of the cell collapse together due to the strengths of the interactions, and the cell stops moving (upper right corner of Fig. 3 a).

Figure 3.

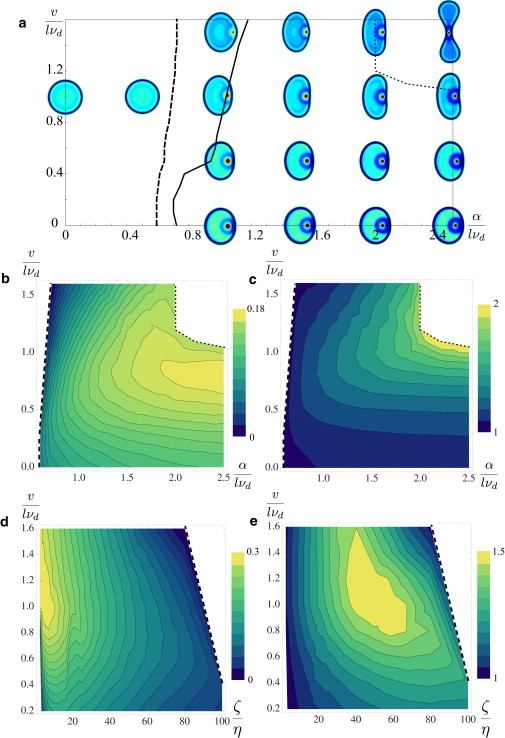
(a) Phase diagram indicated as a function of υ and α. To the left of the solid line, stationary states exist; to the right of the dashed line, moving states exist; in the overlapping region, the two states coexist; and to the right of the dotted line, cell states are collapsed. Filament densities for cell states are color-coded on the diagram. Other parameters are as in Fig. 2. (b–e) Plots of resultant cell speeds and aspect ratios as functions of α, υ, and $1/\eta$, represented as heat maps. Larger cell aspect ratios correspond to more elongated cells. Other parameters are as in Fig. 2. Dashed lines correspond to boundaries with nonmoving states, and dotted lines correspond to boundaries with collapsed states. (b) Cell speed as a function of α and υ. (c) Cell aspect ratio as a function of α and υ. (d) Cell speed as a function of $1/\eta$ and υ. (e) Cell aspect ratio as a function of $1/\eta$ and υ. (Color online.)

In the preceding analysis we examined whether the cell could move in different parameter regimes, but it is also interesting to examine resulting cell velocities and shapes as functions of the parameters. Fig. 3, b and c, indicate cell velocities and aspect ratios in parameter regimes where the cell exhibits a moving state, again, as functions of the treadmilling velocity υ and the strength of interfilament attraction α. We define the cell aspect ratio as the length of the cell measured perpendicular to its velocity divided by that parallel to its velocity; as cells go from round to crescent shaped, this number increases from one. The results show that cell velocities are greatest for intermediate values of υ and large values of α. In addition, cell aspect ratios are large (i.e., the cells are most elongated) for a neighboring regime of values. Although the maximum of cell aspect ratios does not exactly coincide with the maximum of cell speeds, the trend indicates that larger cell aspect ratios correlates with larger cell velocities in most regions of parameter space. Cells collapse when their aspect ratios surpass a critical value.

Because η represents the mobility of filaments in our system, $1/\eta$ is the parameter that corresponds most closely to the adhesion strength between the filaments and the substrate. Thus, it is interesting to examine the cell velocity and aspect ratio also as a function of $1/\eta$ (Fig. 3, d and e). Cell velocities are largest for small values of $1/\eta$ and large values of υ; of interest, velocities are nonmonotonic as functions of $1/\eta$ for small values of υ. Cell aspect ratios are also nonmonotonic, with a maximum for intermediate values of both $1/\eta$ and υ.

Intuition from one dimension

To intuitively explain some features of our model, we discuss a one-dimensional (1D) version of the equations of motion. In this case, the continuous orientation variable θ is replaced by a two-valued discrete variable $s=\pm 1$ indicating whether filaments are oriented along positive or negative x. In Eqs. 1–8, we make the modification $\int d\theta \to {\Sigma }_s$, and for the treadmilling current, we put

$$j_t\left(x,s\right)=s\upsilon c\left(x,s\right).$$ (9)

The boundaries in one dimension are parametrized by two points: $x_L\left(t\right)$ and $x_R\left(t\right)$. The forces on the boundary consist of repulsive interactions with the filaments, as before, whereas forces due to variations of the Helfrich free energy are replaced by a spring force $f_S=k\left(x_R-x_L-L_0\right)$ prescribing a preferred distance L₀ between the two boundary points with spring constant k.

The 1D system, like the 2D system, exhibits both a stationary and a moving asymptotic state. The density profiles of these states are qualitatively similar to the density profiles along the axis of symmetry of the cell in the 2D case. In the stationary state, the total filament density is flat, with some accumulation near the boundaries, and motor density is predominantly flat as well. In the moving state, boundaries and density profiles translate at a constant velocity, with an aggregation of motors and filaments at the back of the cell (see Fig. 4).

Figure 4.

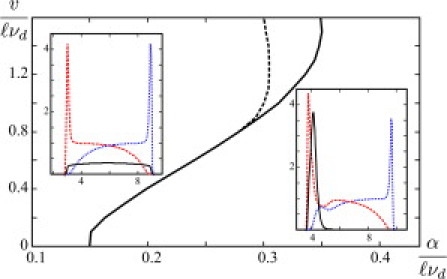
Phase diagram for a 1D system determined as a function of α and υ. To the left of the solid line, stationary states exist. To the right of the dotted line, moving states exist. In the overlapping region, moving and stationary states coexist. Insets depict concentration profiles: motors (black, solid line), right-oriented filaments (blue, dotted line), and left-oriented filaments (red, dashed line). The cell is moving to the right; the length of the cell is $L_0=6\ell$, and $k=1000{\nu }_d/\zeta$. Other parameter values are the same as in Fig. 2. (Color online.)

A phase diagram for the 1D model is presented again as a function of the treadmilling velocity υ and the strength of attractive interactions α, taken to be isotropic. As in the 2D case, it is shown that a nonzero minimum critical value of α is required for moving states to exist. Similarly, α must be below some critical value for stationary states to exist. There is an intermediate region in parameter space of coexistence, in which the asymptotic solutions are bistable.

The 1D problem provides insight into how the system is able to achieve a motile state. Where motor density is low, pressure on the nearby boundary is primarily due to the treadmilling of filaments. However, when motors are localized near one of the boundaries, attractive interactions pull filaments toward each other and therefore away from the boundary, counteracting the effects of treadmilling on filament current and resulting in reduced net pressure on the boundary. The difference between forces on the two boundaries leads to a net velocity of the cell. The boundary closer to the aggregate of motors consequently becomes the back of the cell, and the boundary farther from the motors becomes the front.

We can test this intuitive argument by making an “infinite cell approximation”, in which we solve for the force-velocity relation for single boundaries of two types, “front” and “back”, with motor densities approximating those seen in the front and back of the motile 1D cell. For the front boundary at position $x=x_R$, the density of the motors is set identically to zero. For the rear boundary at $x=x_L$, we do not require the motor density to vanish. We consider an infinite domain with filaments nucleating to the left of the boundaries $x<x_R$ for the front, and $x<x_L$ for the back. We impose the following boundary conditions on the density fields: $c\left(-\infty ,\pm 1\right)={\nu }_0/{\nu }_d$, and $c\left(\infty ,\pm 1\right)=0$. Prescribing some boundary velocity V, we solve for the corresponding filament density profiles and obtain the resultant forces $f_R\left(V\right)$, acting on the front boundary, and $f_L\left(V\right)$, acting on the back boundary. To derive the force-velocity relation for a moving cell, we require that $2{\upsilon }_{cell}/\zeta =f_R\left({\upsilon }_{cell}\right)-f_L\left(-{\upsilon }_{cell}\right)$. This amounts to assuming that the front and the back of the cell interact exclusively through the spring force that holds the boundaries together. Fig. 5 presents a comparison of cell velocity calculated in the infinite cell limit with that obtained from simulations of cells of length $10\ell$. These are in close agreement. Therefore, the difference in net pressures on the boundaries caused by different motor concentrations appears to be sufficient to drive forward motion.

Figure 5.

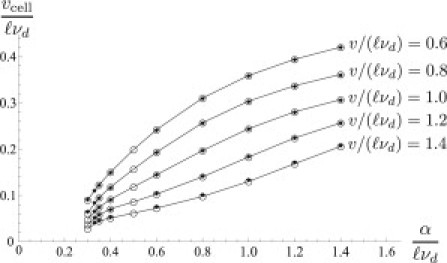
Solid diamonds indicate the velocities of a cell of length $10\ell$ in a 1D system as a function of α. The open circles connected by lines indicate the velocities of an “infinite cell”, calculated by treating “front” and “back” boundaries separately. Other parameters are as in Fig. 4.

Biological implications

The system we have defined consisting of filaments, motors, and boundaries exhibits characteristic features reminiscent of live cells. Of importance, the system is self-organized: cell polarization and motility arise naturally out of local interactions assigned to filaments and motors. Furthermore, the mechanism that drives polarization and motility in our model is an attractive, motor-mediated interaction between filaments, which leads to contractile behaviors of the filament network. In fact, it has been proposed that network contractility at the rear of the cell drives motility (7,8). In addition, our system exhibits both stationary and moving states; within the moving states, motors are localized to the back of the cell, and the front edge is driven by treadmilling filaments, as observed in experiments (13).

It has been observed that keratocyte fragments may sometimes be switched between motile and nonmotile behaviors by mechanical stimulation (13). Our model exhibits bistability between these states, but only in intermediate parameter regimes. From our 2D phase diagram (Fig. 3 a), we predict that with increasing myosin activity, cells would go from a completely immobile state, to a bistable regime, to a completely mobile state. One could test this prediction experimentally by pharmacologically varying the myosin activity, such as by using blebbistatin to lower activity, or calyculin A to raise it. The fraction of cells that are moving in an environment that is noisy enough to toggle cells between moving and nonmoving states could then be measured for different drug concentrations.

Recent work has begun to describe the effects of experimental conditions on cell shape and speed of moving keratocytes. Experiments in which substrate adhesivity was changed showed that cell aspect ratios and velocities vary nonmonotonically as functions of adhesion strength, with maxima at moderate adhesion levels (32). In agreement with these experiments, our model shows cell aspect ratios to be nonmonotonic functions of adhesion strength (Fig. 3 e), and we additionally find that cell velocities are nonmonotonic functions of adhesion strength for small and intermediate values of the treadmilling speed (Fig. 3 d). Using calyculin A and blebbistatin to modulate myosin activity, investigators have shown experimentally that increased myosin activity results in increased cell velocities. This result is also predicted by our model, as shown in Fig. 3, b and c. However, our model disagrees with some previous results from experiments, in that in those experiments, cells became rounder when myosin activity was increased (32), whereas in the model, increasing myosin activity causes the cell to become more elongated (Fig. 3 c). This difference may be explained by a more lateral distribution of myosin in vivo due to the position of the nucleus, or by changes in the 3D shape of the cell that cannot be captured in our 2D model.

In addition to the above comparisons with previous experiments, our model suggests other experiments that may be conducted in the future. Relatively little work has been done to examine how cell velocities and shapes respond to changes in the rate of actin polymerization. From Fig. 3, b–e, we expect that in response to changing actin polymerization rates, cell velocity and aspect ratio would change nonmonotonically, with maxima at intermediate values of polymerization rates. Furthermore, for higher myosin activities, the peak of cell velocity or aspect ratio should occur at higher polymerization rates. Another prediction is that increasing myosin activity beyond a critical value would collapse the cell and stop movement. These predictions could all be tested in experiments in which actin polymerization or myosin activity is modified pharmacologically.

Further theoretical and numerical work may offer additional insight into other mechanisms of cell motility. Although myosin aggregation is central to our model, other mechanisms of motility, described in models and experiments (4,31), do not include myosin aggregation. In particular, Doubrovinski and Kruse (31) proposed a model in which motility arises through a combination of filament treadmilling and cooperatively binding nucleators. The dynamics predicted by this system differs from the dynamics predicted here. For example, the nucleator-based system admits traveling-wave solutions when the bounding domain is stationary, whereas the myosin-based model described here does not. Also, the myosin-based model exhibits “retrograde flow”, that is, filaments are transported by motors toward regions of high motor density; this behavior is absent in the nucleator-based model. In live cells, motility is most likely due to both myosin and nucleator dynamics. The contributions of these mechanisms could be determined pharmacologically or genetically; alternatively, filament dynamics under different conditions could be examined by speckle microscopy and compared with model predictions.

Conclusions

We have presented a mathematical description of filaments, motors, and membranes in an effort to elucidate the self-organized mechanisms involving cytoskeletal networks that drive cell polarization and motility. In the system defined here, motors mediate attractive interactions between filaments. These interactions destabilize the stationary state and give rise to spontaneous polarization of the system. Our system exhibits both stationary and moving asymptotic states, in qualitative agreement with living cells. The resulting localization of molecular components is also in qualitative agreement with experimental observations. Our analysis suggests that motor-mediated contractility of filament networks may drive cell motility. More generally, our description shows that local interactions of molecular components may be sufficient to determine cell-level organization.

Our model predicts the dependence of cell speeds and shapes on parameters that physically correspond to myosin motor activity, actin polymerization rate, and adhesive properties of the substrate. Some of the trends indicated in the model's results have been revealed in previous experiments, but the model also makes predictions that remain to be tested by experiment. We have proposed a few such experiments in the text.

In this work we explored, using a simple model, how whole-cell behavior may arise through local cytoskeletal interactions, but we did not thoroughly examine cellular interactions with the surrounding environment. In the future, it would be interesting to see whether extensions of our physical description can help explain the response of cells to their environment.

Appendix A: Treatment of the Boundary

The force density on the boundary $\mathit{f}={\mathit{f}}_H+{\mathit{f}}_I$ has two contributions. The Helfrich free energy $\mathcal{F}(\Gamma )=\sigma L+\kappa \int d\Gamma H^2+P{\left(A-A_0\right)}^2$ depends only on the positions of the boundary and physical parameters. The forces on the boundary due to surface tension, bending stiffness, and area constraint are then derived from variation of the Helfrich energy with respect to the shape of the boundary Γ (30). We parametrize Γ as $\mathbf{x}\left(s\right)\equiv \left(x\left(s\right),y\left(s\right)\right)$. The Helfrich energy is then written as

$$\mathcal{F}=\sigma \int ds\left|{\mathit{x}}^{\mathit{\prime }}\right|+\kappa \int ds\left|{\mathit{x}}^{\mathit{\prime }}\right|H^2+P{\left(\frac{1}{2}\int ds\left|{\mathit{x}}^{\mathit{\prime }}\right|\mathit{x}·\hat{\mathit{n}}-A_0\right)}^2,$$ (10)

where the local curvature is denoted by the function $H=\left(x^{\prime }{y}^{″}-y^{\prime }{x}^{″}\right)/{\left(x^{\prime 2}+y^{\prime 2}\right)}^{3/2}$, which is a function of only ${\mathit{x}}^{\mathit{\prime }}$ and ${\mathit{x}}^{\mathit{″}}$, and the vector $\hat{n}=\left(-y^{\prime },x^{\prime }\right)/\left|{\mathit{x}}^{\prime }\right|$, which denotes the outward unit normal. Here, we used the divergence theorem to calculate the area A:

$$A=\frac{1}{2}\underset{\text{cell}}{\int }d\mathit{r}\left(\nabla ·\mathit{r}\right)=\frac{1}{2}\underset{\Gamma }{\int }ds\left|{\mathit{x}}^{\mathit{\prime }}\right|\left(\mathit{x}·\hat{\mathit{n}}\right).$$ (11)

The force density on the boundary at point x is obtained by taking the variation of ℱ with respect to the parametrization x and dividing by the line element $ds\left|{\mathbf{x}}^{\prime }\right|$. Let ${\mathit{f}}_H$ denote the force per unit length on the boundary due to the Helfrich energy:

$${\mathit{f}}_H\left(\mathbf{x}\right)=\frac{1}{ds\left|{\mathit{x}}^{\mathit{\prime }}\right|}\left(-\frac{\delta \mathcal{F}}{\delta \mathit{x}}\right)=\frac{\sigma }{\left|{\mathit{x}}^{\mathit{\prime }}\right|}\frac{d}{ds}\left({\nabla }_{{\mathit{x}}^{\mathit{\prime }}}\left|{\mathit{x}}^{\mathit{\prime }}\right|\right)+\frac{\kappa }{\left|{\mathit{x}}^{\mathit{\prime }}\right|}\left(\frac{d}{ds}{\nabla }_{{\mathit{x}}^{\mathit{\prime }}}\left(\left|{\mathit{x}}^{\mathit{\prime }}\right|H^2\right)-\frac{d^2}{d{s}^2}{\nabla }_{{\mathit{x}}^{\mathit{″}}}\left(\left|{\mathit{x}}^{\mathit{\prime }}\right|H^2\right)\right)+\frac{2P\left(A-A_0\right)}{\left|{\mathit{x}}^{\mathit{\prime }}\right|}(-{\nabla }_x\left(\left|{\mathit{x}}^{\mathit{\prime }}\right|\mathit{x}·\hat{n}\right)+\frac{d}{ds}{\nabla }_{{\mathit{x}}^{\mathit{\prime }}}\left(\left|{\mathit{x}}^{\mathit{\prime }}\right|\mathit{x}·\hat{n}\right))).$$ (12)

This computes to

$${\mathit{f}}_H\left(\mathit{x}\right)=-\sigma H\hat{\mathit{n}}-\kappa g\left(\mathit{x}\right)\hat{\mathit{n}}-2P\left(A-A_0\right)\hat{\mathit{n}},$$ (13)

where

$$g\left(\mathit{x}\right)=\left(-\frac{1}{y^{\prime }},\frac{1}{x^{\prime }}\right)·\frac{d}{ds}\left(-\frac{H}{\left|{\mathit{x}}^{\prime }\right|}{\hat{\mathit{n}}}^{\prime }+2\frac{H^{\prime }}{\left|{\mathit{x}}^{\prime }\right|}\hat{\mathit{n}}\right),$$ (14)

and primes again denote derivative with respect to the parametrizing variable s. In the implementation of the numerics, the curve $\mathit{x}\left(s\right)$ is given by a set of discrete points $\left\{{\mathit{x}}_i\right\}$, so that the boundary looks like a many-sided polygon with vertices $\left\{{\mathit{x}}_i\right\}$. The expression for force density on the right-hand side of Eq. 12 is explicitly evaluated at points x_i and multiplied by the length element $\left(\left|{\mathit{x}}_{i+1}-{\mathit{x}}_i\right|+\left|{\mathit{x}}_i-{\mathit{x}}_{i-1}\right|\right)/2$ to obtain the total force applied to a boundary point at each time step. Evaluation of the right-hand side of Eq. 12 can be computed by taking $x^{\prime }=\left(x_{i+1}^x-x_{i-1}^x\right)/2$, and so forth.

The second contribution to forces on the boundary comes from interactions with the filaments. If the curve Γ again has coordinates defined parametrically by the function $\mathit{x}\left(s\right)$, then the filament-boundary interaction energy can be written as

$${\mathcal{F}}_I=\int d\mathbf{r}{c}_T\left(\mathbf{r}\right)V\left(d\left(\mathit{x}\left(s\right),\mathbf{r}\right)\right),$$ (15)

where the function V is a sigmoidal function describing the rise of the repulsive potential between filaments and the boundary in the vicinity of the cell boundary. The function d is the signed distance between point r and the boundary of the cell at x, where d is negative for r inside the cell boundary and positive outside of the cell boundary. The density $c_T\left(\mathbf{r}\right)$ denotes the total filament density at r, so $c_T=\int d\theta c\left(\mathbf{r},\theta \right)$.

The force ${\mathit{F}}_I^{{\mathit{x}}_i,\mathbf{r}}$ applied to a boundary element at point x_i on the curve x(s) due to interactions with filaments in a small volume dr is determined by varying Eq. 15 with respect to x and evaluating at the point x_i. This evaluation will be zero unless x_i is the closest point on x to r, so assuming that x_i is the closest point on the curve to r, then $d=\left|\mathbf{r}-{\mathit{x}}_i\right|$ and

$${\mathit{F}}_I^{{\mathit{x}}_i,\mathbf{r}}=-d\mathbf{r}{c}_T\left(\mathbf{r}\right){\nabla }_{{\mathit{x}}_i}V\left(d\left(\mathit{x},\mathbf{r}\right)\right)=-d\mathbf{r}{c}_T\left(\mathbf{r}\right)\frac{\partial V}{\partial d}{\nabla }_{{\mathbf{x}}_i}\left|\mathbf{r}-{\mathit{x}}_i\right|.$$ (16)

The total force $\mathbf{F}\left(\mathbf{r}\right)$ on filaments in a volume dr due to the boundary is minus the gradient of the potential multiplied by the number of filaments $d\mathbf{r}{c}_T\left(\mathbf{r}\right)$:

$$\mathbf{F}\left(\mathbf{r}\right)=-d\mathbf{r}{c}_T\left(\mathbf{r}\right){\nabla }_{\mathbf{r}}V\left(d\left(\mathit{x},\mathbf{r}\right)\right).$$ (17)

The contribution to the total force due to an element of the boundary at x_i is zero if x_i is not the closest point on the boundary to r, and is equal to the following if it is:

$${\mathit{F}}_I^{\mathbf{r},{\mathit{x}}_i}=-d\mathbf{r}{c}_T\left(\mathbf{r}\right)\frac{\partial V}{\partial d}{\nabla }_{\mathbf{r}}\left|\mathbf{r}-{\mathit{x}}_i\right|.$$ (18)

From Eqs. 16 and 18, it follows that

$${\mathit{F}}_I^{{\mathit{x}}_i,\mathbf{r}}=-{\mathit{F}}_I^{\mathbf{r},{\mathit{x}}_i},$$ (19)

implying that the force on the filaments at r due to the boundary element at x_i is equal to the force on the boundary element at x_i due to filaments at r.

Appendix B: Numerical Methods

The numerical solutions to Eqs. 1–8 are obtained from simulations on a 128 × 128 grid. Periodic boundary conditions in both dimensions are imposed. The angular spacing for numerical simulations is discretized into eight angles. The cell boundary is parametrized by 40 points, and boundary-filament interactions are treated numerically via a repulsive potential as described above. More details can be found in Doubrovinski and Kruse (31). We put

$$-\nabla V\left(\left|\mathbf{d}\right|\right)=F_0{e}^{-{\left(\left|\mathbf{d}\right|\right)/d_0)}^4}\hat{\mathbf{d}}.$$ (20)

The vector $\mathbf{d}\equiv \mathbf{d}\left(\Gamma ,\mathbf{r}\right)$ refers to the shortest vector from the boundary Γ to a point r in the simulation domain. In the case where the boundary is parametrized by points $\left\{{\mathit{x}}_i\right\}$, the vector d may be either the normal vector from a line segment joining adjacent points on the boundary to the point r, or the vector from a point x_i on the boundary to r. The numerical parameters F₀ and d₀ are chosen to make the boundary approximately reflecting within the practical requirements of numerical stability, that is, we choose $F_0\gg 1$ and $d_0\ll 1$.

We nondimensionalize the parameters by expressing length in units of ℓ, expressing time in units of $1/{\nu }_d$, and expressing forces in units of $\ell {\nu }_d/\zeta$. In the simulations, filaments nucleate at a rate ν₀ only within the boundary and at least a distance d₀ from the boundary; this is to ensure that no forces are introduced on the boundary due to nucleation effects. The integrals over ${\mathbf{r}}^{\prime }$ in Eq. 4 are computed with the use of Fourier transforms. For simplicity, we take α to be isotropic in the simulations. In this case, the ${\theta }^{\prime }$ integral in Eq. 4 becomes trivial. However, the ${\mathbf{r}}^{\prime }$ integral remains a convolution, which we rewrite in terms of Fourier transforms; for example, if we put $c_T\left(\mathbf{r}\right)\equiv \int d{\theta }^{\prime }c\left(\mathbf{r},{\theta }^{\prime }\right)$, then the second term in Eq. 4 contains the factor

$$\int d{\mathbf{r}}^{\prime }f\left({\mathbf{r}}^{\prime }-\mathbf{r}\right)c_T\left({\mathbf{r}}^{\prime }\right)={\mathcal{F}}^{-1}\left[\mathcal{F}\left[f\left(\mathbf{r}\right)\right]\times \mathcal{F}\left[c_T\left(\mathbf{r}\right)\right]\right],$$ (21)

which we can numerically compute more efficiently using the Fourier transform and the FFTW subroutine library. 2D transforms are formulated as a set of 1D transforms. All numerical work is performed in C++.