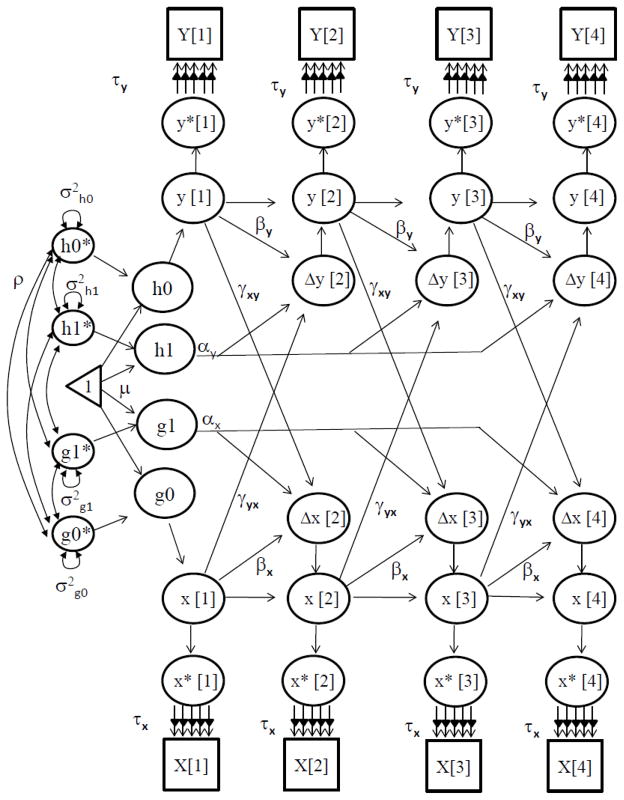
Figure 1.
A bivariate dual change score model for categorical response variables over grade-level in two measured variables (Y and X). Notes: αy and αx represent constant change related to the slope factors ys and xs; βy and βx represent proportional change in Y and X; cross-trait coupling is indicated by γyx and γxy. g1 and h1 are the latent slope scores that are constant over time, and the changes are based on additive parameters (αy and αx), self-feedback parameters (βy and βx), and coupling parameters (γyx and γxy). Δx and Δy indicate latent change scores of X and Y, respectively. τx and τy indicate the thresholds for X and Y, respectively. Error variance (ψ2) is assumed to be constant at each grade level within each factor. The model includes estimates for intercepts (y0 and x0), mean intercepts (μy0 and μx0), and mean slopes (μy1 and μx1). Other parameters are used to generate the decomposition of the correlation between the intercept and slope for X and Y. * indicates latent response strength that is estimated based on ordinal response variables.