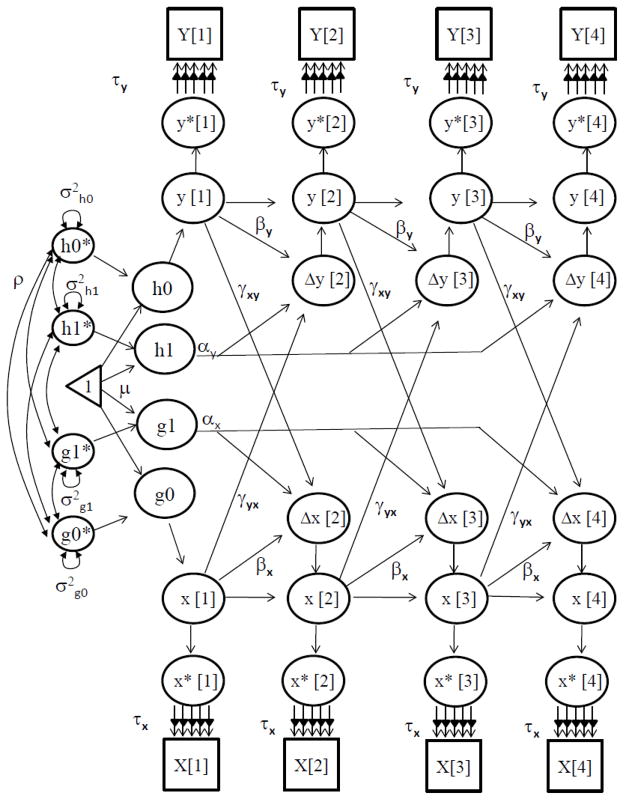
Figure 1.

A bivariate dual change score model for categorical response variables over grade-level in two measured variables (Y and X). Notes: α_y and α_x represent constant change related to the slope factors y_s and x_s; β_y and β_x represent proportional change in Y and X; cross-trait coupling is indicated by γ_yx and γ_xy. g₁ and h₁ are the latent slope scores that are constant over time, and the changes are based on additive parameters (α_y and α_x), self-feedback parameters (β_y and β_x), and coupling parameters (γ_yx and γ_xy). Δx and Δy indicate latent change scores of X and Y, respectively. τ_x and τ_y indicate the thresholds for X and Y, respectively. Error variance (ψ²) is assumed to be constant at each grade level within each factor. The model includes estimates for intercepts (y₀ and x₀), mean intercepts (μ_y0 and μ_x0), and mean slopes (μ_y1 and μ_x1). Other parameters are used to generate the decomposition of the correlation between the intercept and slope for X and Y. * indicates latent response strength that is estimated based on ordinal response variables.