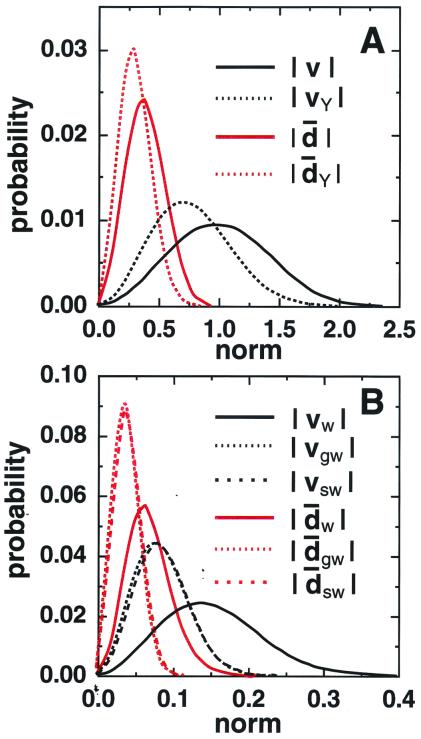
Figure 3.

Distributions of amplitude of the site dipoles in the MD model and in the noncorrelated model. The noncorrelated models were calculated by placing a randomly oriented unit vector u on each oxygen atom of moving water molecules along the MD trajectory. The orientations of u were changed by gradual or sudden rotation. In the gradual rotation, the orientation was renewed at each step of trajectory as u → u′ = u + Δu, where Δu was a small random vector and u′ was normalized as  u′  = 1. In the sudden rotation, u was randomly rotated at each step of trajectory with a small probability ɛ. The rotational relaxation time of u was set to the value (5.2 ps) in the current simulation in both rotations with modulating Δu or ɛ. (A) Distributions of amplitude of the coarse-grained site dipoles in the MD model, |d̄(r_i,R)|, and in the noncorrelated model, |d̄_Y(r_i,R)|, and distributions of amplitude of the vorticities in the MD model, |v(r_i,R)|, and in the noncorrelated model, |v_Y(r_i,R)| (R = 4L_cube). Either gradual or sudden rotation provides exactly the same results. (B) Distributions of amplitude of the coarse-grained, time-averaged site dipoles in the MD model, |d̄_w(r_i,R)|, and in the noncorrelated model, |d̄_Yw(r_i,R)|, and distributions of amplitude of the time-averaged vorticities in the MD model, |v_w(r_i,R)|, and in the noncorrelated model, |v_Yw(r_i,R)|. Here, Y = “g” for the gradual rotation of the noncorrelated model and Y = “s” for the sudden rotation. w = 300 ps and R = 4L_cube.