Figure 4.

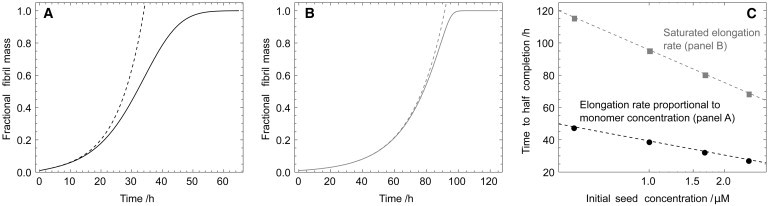
Effect of the saturation of the elongation rate on the time course of the reaction, and comparison with the well-known linearized solution to the rate equations (29,18,15). (A) Time course computed numerically (17) (solid line) for the aggregation reaction for the case where the elongation rate depends linearly on the monomer concentration (16). In this case, the linearized solution (dotted line), from Eq. 2, is only accurate for the early part of the reaction time course. A self-consistent solution has been derived previously that is accurate for the full time-course in this case (16). (B) Time-course computed numerically (17) (solid line) for the case where the elongation rate is saturated (39) and does not depend on the monomer concentration. In this case, the nonlinearity in the rate equations (17) is reduced, increasing the range of validity of the linearized solution (dotted line), from Eq. 2. (C) Scaling of the half-time with the seed concentration calculated numerically for the cases shown in panels A (solid) and B (shaded). In both cases a logarithmic scaling, from Eq. 7, is found. In panel A, ${\tilde{k}}_{+}=k_{+}$ with k₊ = 5 · 10³k₊ = 1 M⁻¹ s⁻¹; in panel B, ${\tilde{k}}_{+}=k_{+}/\left[1+m\left(0\right)/K_m\right]$ with K_m = m(0)/10 and k₊ = 1 · 10⁴k₊ = 1 M⁻¹ s⁻¹. For panels A and B, the other parameters are: m(0) = 50 μM, k₋ = 2 · 10⁻⁹ s⁻¹, k_n = 0, n₂ = 0, M(0) = m(0)/100, and P(0) = M(0)/5000. Panel C has parameters from panel A (shaded) and panel B (solid), respectively, except for the varying seed (mass) concentrations shown.