Fig. 6.

Oscillations in input due to refractoriness and resonance of integrate-and-fire model neurons. (a) Power spectral density (PSD) of the superposition of exc. and inh. PPDs which are used as input, theoretical curves Eq. (46) computed analogously to Eq. (34). Subplots correspond to different relative dead-times 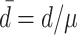 of the input components as indicated on the left. Colors distinguish the rate of component input PPDs as in Fig. 5(c). (b) PSD of the membrane potential of population 1 in units of mV2 s − 1 driven by PPD superpositions. Error-bars show the standard deviation of the estimate across LIF neurons. Solid line shows the analytical power spectrum computed via Eq. (47), computed analogously to Eq. (34). Subplots and colors as in (a). (c) Estimated PSD of the output spike trains of population 2 in units of s − 1 driven by PPD superpositions. Subplots and colors as in (a). Error-bars display standard deviation of the estimate across neurons. (d) Interval statistics (mean ISI μ
n and coefficient of variation CVn) and matched PPD parameters (λ
n, d
n) of population 2 neurons’ output spike trains for several
of the input components as indicated on the left. Colors distinguish the rate of component input PPDs as in Fig. 5(c). (b) PSD of the membrane potential of population 1 in units of mV2 s − 1 driven by PPD superpositions. Error-bars show the standard deviation of the estimate across LIF neurons. Solid line shows the analytical power spectrum computed via Eq. (47), computed analogously to Eq. (34). Subplots and colors as in (a). (c) Estimated PSD of the output spike trains of population 2 in units of s − 1 driven by PPD superpositions. Subplots and colors as in (a). Error-bars display standard deviation of the estimate across neurons. (d) Interval statistics (mean ISI μ
n and coefficient of variation CVn) and matched PPD parameters (λ
n, d
n) of population 2 neurons’ output spike trains for several 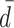 (blue, green, red, cyan, orange: 0.0, 0.2, 0.4, 0.6, 0.8) as a function of the rate 1/μ of the component input PPDs. Same parameters and simulation setup as in Fig. 5
(blue, green, red, cyan, orange: 0.0, 0.2, 0.4, 0.6, 0.8) as a function of the rate 1/μ of the component input PPDs. Same parameters and simulation setup as in Fig. 5
