Operation of the alula as an indicator of gear change in hoverflies

Abstract

The alula is a hinged flap found at the base of the wings of most brachyceran Diptera. The alula accounts for up to 10 per cent of the total wing area in hoverflies (Syrphidae), and its hinged arrangement allows the wings to be swept back over the thorax and abdomen at rest. The alula is actuated via the third axillary sclerite, which is a component of the wing hinge that is involved in wing retraction and control. The third axillary sclerite has also been implicated in the gear change mechanism of flies. This mechanism allows rapid switching between different modes of wing kinematics, by imposing or removing contact with a mechanical stop limiting movement of the wing during the lower half of the downstroke. The alula operates in two distinct states during flight—flipped or flat—and we hypothesize that its state indicates switching between different flight modes. We used high-speed digital video of free-flying hoverflies (Eristalis tenax and Eristalis pertinax) to investigate whether flipping of the alula was associated with changes in wing and body kinematics. We found that alula state was associated with different distributions of multiple wing kinematic parameters, including stroke amplitude, stroke deviation angle, downstroke angle of incidence and timing of supination. Changes in all of these parameters have previously been linked to gear change in flies. Symmetric flipping of the alulae was associated with changes in the symmetric linear acceleration of the body, while asymmetric flipping of the alulae was associated with asymmetric angular acceleration of the body. We conclude that the wings produce less aerodynamic force when the alula is flipped, largely as a result of the accompanying changes in wing kinematics. The alula changes state at mid-downstroke, which is the point at which the gear change mechanism is known to come into effect. This transition is accompanied by changes in the other wing kinematic parameters. We therefore find that the state of the alula is linked to the same parameters as are affected by the gear change mechanism. We conclude that the state of the alula does indeed indicate the operation of different flight modes in Eristalis, and infer that a likely mechanism for these changes in flight mode is the gear change mechanism.

1. Introduction

Insects achieve their remarkable manoeuvrability and control through changes in their wing kinematics; yet the wings are passive structures with no internal muscles. Instead, all of their control inputs operate through the exquisitely intricate wing hinge (figure 1a). A combination of some 20 accessory muscles manipulate the wingbeat by acting upon the hardened, articulated pieces of cuticle called sclerites that form the wing hinge. The functions of certain of these sclerites and accessory muscles have been studied in detail, but there is still no consensus on exactly how the wing hinge operates during a typical wing stroke [3]. Pfau [4] has proposed that the operation of the dipteran wing hinge is associated with a gear change mechanism in which the wing hinge elements articulate differently in the different gears, thereby altering the wing kinematics. Although our understanding of other aspects of the operation of the wing hinge has since changed [5,6], the wingbeat of many higher Diptera does indeed appear to involve a gear change mechanism [1,7]. The presence of a gear change mechanism has sometimes been questioned [3], but recent electrophysiological recordings of the steering muscles have provided indirect evidence for this in Calliphora [8].

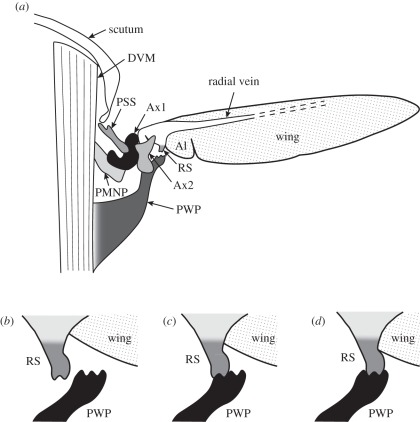
Figure 1.

(a) Simplified illustration of a transverse section of the dipteran thorax. The wing hinge is exquisitely intricate and involves movement of multiple sclerites, actuated by various steering muscles (not shown). The gear change mechanism involves the interaction of the radial stop (RS) and the pleural wing process (PWP) at mid-downstroke. These gear changes are thought to be controlled by the muscles that actuate the first axillary sclerite (Ax1) and the third axillary sclerite (not visible). (b–d) Enlargement of the wing hinge showing the three possible positions of the RS relative to the PWP at mid-downstroke, corresponding to three distinct gears in Calliphora. DVM, dorsoventral muscle; PSS, parascutal shelf; Al, Alula; Ax2, second axillary sclerite; PMNP, post-median notal process. Modified from Nalbach [1] and Miyan & Ewing [2].

The gear change mechanism involves the mechanical interaction of two sclerites: the radial stop, which is a projection emerging from the wing ventral to the radial vein, and the pleural wing process, which is a thoracic sclerite formed by the dorsal end of the pleural plate [2]. These two sclerites do not appear to make contact at all during a normal wingbeat in Calliphora [1], but the radial stop is sometimes observed to engage with the pleural wing process during the lower half of the stroke. When this occurs, the pleural wing process acts as a mechanical stop, limiting the downward movement of the wing [2]. The pleural wing process of Calliphora has two grooves on its surface, and the sclerites appear to engage in one of three principal gears [1], according to whether the radial stop is engaged in the anterior or posterior groove of the pleural wing process (figure 1c,d), or is not engaged at all (figure 1b). The precise details of the gear change mechanism appear to vary across species [2,6]. In Eristalis, for example, the pleural wing process has only one groove [2], which might suggest the existence of two, rather than three, distinct modes in this species.

In Calliphora, the three distinct modes are each associated with different wing kinematics [1]. In particular, Nalbach [1] found that the stroke angle at the end of the downstroke was tri-modally distributed in tethered Calliphora. Stroke angle at the end of the downstroke is highly correlated with stroke amplitude in flies, which tend to vary the position of the lower, rather than upper, turning point of the stroke cycle in order to vary stroke amplitude [9,10]. The gear change mechanism seems therefore to be intimately tied up with changes in stroke amplitude. Gear changes in Calliphora are also associated with delayed supination at the end of the upstroke, and may well involve other changes to the wing kinematics that were not measured by Nalbach [1]. Nalbach [1] reported that gear change appeared to be used mostly during fictive turns in tethered insects, with the inside wing operating with the radial stop and pleural wing process engaged on the downstroke with a reduced stroke amplitude. Stroke amplitude is considered a key variable in determining flight forces [9,11]; so the reduced stroke amplitude associated with the gear change mechanism would be expected to result in reduced aerodynamic forces.

Switching between the different gears is apparently controlled by the axillary muscles, with the muscles of the first axillary sclerite capable of producing the required changes to the operation of the wing hinge [1,2]. However, the third axillary sclerite has been found always to move during gear change; so the muscles of the third axillary sclerite are also likely to be involved in gear change [1]. This conclusion is supported by electrophysiological recordings and high-speed film of tethered Calliphora, which showed distinct changes in the stroke amplitude and deviation angles associated with the firing pattern of muscles actuating the first and third axillary sclerites [8].

Previous work on the wing hinge mechanism has been limited to tethered flight, because of the difficulty associated with making observations of the wing hinge or electrophysiological measurements in small free-flying insects. The functional significance of gear change therefore remains unknown in relation to the control of body kinematics. Most wing kinematic parameters vary in a continuous fashion, which makes them ill-suited to identifying the operation of a particular flight mode in free flight. However, Walker et al. [12,13] recently observed that a hinged flap found near the base of the wing in the drone fly, Eristalis tenax L. operated in one of two binary states during free flight. This flap, called the alula, is a prominent feature of the wings of most brachyceran flies, and accounts for up to 10 per cent of the wing surface in hoverflies (figure 2). Microscopic examination of the wing hinge reveals that the state of the alula is controlled directly by the third axillary sclerite (figure 3). We therefore hypothesize that the state of the alula during flight indicates the position of the third axillary sclerite, and can consequently be used to identify operation of the gear change mechanism itself. In this paper, we use high-speed digital videography of free-flying hoverflies (E. tenax and Eristalis pertinax, Scopoli) to investigate whether the two states of the alula are associated with different modalities in the wing kinematics, and with differences in body kinematics.

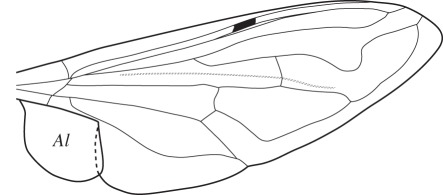
Figure 2.

Drawing of the right wing of Eristalis tenax showing location of the alula (Al). The distal portion of the alula overlaps dorsally the adjacent part of the wing.

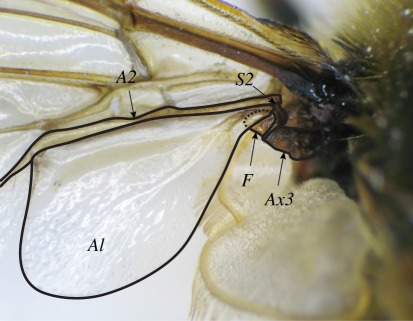
Figure 3.

Magnified view of the left wing of Eristalis tenax, showing the attachment of the alula (Al) to the rest of the wing. The third axillary sclerite (Ax3) is fused to a sclerotized region (S2) of the second anal vein (A2). A flexible section of cuticle (F) protrudes from this fused joint, and forms a socket for a raised protrusion of the alula (dotted line) created by folding of the cuticle. Manipulation of the S2–Ax3 complex causes the flexible section of cuticle to rotate, and the alula to flip.

2. Material and methods

2.1. Experimental set-up

Eristalis tenax and E. pertinax hoverflies (Diptera: Syrphidae) were wild-caught in Oxford. The hoverflies were stored in a cooler at 12°C and fed on sugar solution. All insects were flown within three weeks of capture. Individual hoverflies were released inside a 1 m diameter opaque acrylic sphere, in which they were allowed to fly freely. A typical flight consisted of slow forward flight punctuated by rapid saccades, which are fast manoeuvres characteristic of dipteran flight [11,14,15]. We also observed hovering behaviours, fast forwards flight and backwards flight. Individuals varied greatly in their behaviour: while some were content to fly continuously around the sphere, others would only fly intermittently and had to be encouraged to fly by tactile stimulation. Maximum flight speed was up to about 1 m s⁻¹, with maximum horizontal accelerations approaching 1g. These values are similar to those measured for hoverflies, including E. tenax flying freely in the wild [16,17]. The data therefore cover a wide gamut of flight performance, although we do not necessarily expect to have explored the flight envelope fully.

Four Photron SA3 cameras (Photron Ltd, Bucks, UK) with 180 mm Sigma macro lenses were used to film the hoverflies, recording at 3800 frames per second with 768 × 640 pixel resolution. Four portholes were cut in the upper part of the sphere and were covered with 0.175 mm clear sheet polyester to allow viewing by the cameras. An LED light source was fixed to the inside of the upper surface of the arena to encourage hoverflies to fly below it in the region visible to the cameras. Illumination for the cameras was provided by two synchronized 200 W infrared pulsed lasers (HSI-5000, Oxford Lasers Ltd, Oxford, UK), each of which was routed through split liquid light guides before being collimated by a large Fresnel lens. This provided extremely bright back-illumination, while the 20 µs pulse duration eliminated motion blur and prevented overheating of the insect. The wavelength of the laser (805 nm) was far beyond the range of the visible spectrum for Eristalis (upper limit: 600 nm [18–21]) and the laser frequency (3800 Hz) was in any case several orders of magnitude greater than the flicker fusion frequency of Eristalis (ca 160 Hz [22]).

The cameras were calibrated using custom-written software running in Matlab (Matlab v. 7.4, The Mathworks Inc., Natick, MA, USA) to produce jointly optimal estimates of the camera parameters and the spatial coordinates of points on a two-dimensional calibration grid in a range of positions and orientations [12,13].

2.2. Automatic reconstruction of wing and body coordinates

In total, 854 video sequences from 36 hoverflies were selected for analysis, which included all sequences in which both wings were visible for one or more wingbeats in all four cameras. The full dataset includes a total of 26 236 wingbeats. A fully automated shape-carving procedure was used to reconstruct the positions of the body and the wing outlines, similar to the hull reconstruction technique described by Ristroph et al. [23] but with certain modifications to allow us to measure wing twist. We used background subtraction and automatic thresholding to isolate the hoverfly body in each camera view, and used a shape-carving algorithm to calculate the voxels corresponding to the body. We identified the wings by using the shape-carving algorithm to calculate the voxels corresponding to the wings and body together, and then removing those voxels that had already been identified as belonging to the body at the previous step. This sequential procedure ensured that information was not lost when the wing was occluded by the body in one or more camera views, as would occur if the silhouettes of the wings alone were used to identify the position of the wings. The voxels corresponding to the wings do not have the same thinness as the real wings, unless the wing chord happens to be perpendicular to one of the image planes [23]. We therefore used the wing voxels to identify the outlines of the wings in the original images, and used the shape-carving algorithm on these outlines to produce a three-dimensional outline corresponding precisely to the leading and trailing edges of the wing.

2.3. Measurement of body kinematics

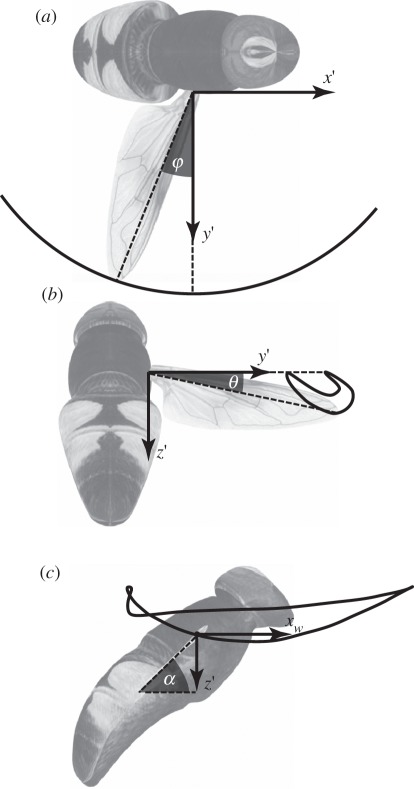
Measurements of the body kinematics were made using a right-handed, body-fixed axis system (figure 4). The origin of the axis system was fixed at the centre of volume of the body voxels. The x-axis pointed anteriorly and was defined by the major axis of the body, calculated using principal components analysis on the body voxels. The y-axis was defined as the axis parallel to the line joining the wing bases (figure 4). We measured the position and orientation of the body axes relative to laboratory coordinates, using a sequence of Euler angles measuring azimuth, elevation and bank angle, in that order. We then smoothed our measurements of position and orientation using a quintic smoothing spline, with a tolerance factor calculated from the residuals of fitting a third-order Butterworth filter with a cut-off frequency of 80 Hz for the body parameters and 800 Hz for the wing parameters. The 80 Hz filter frequency was selected to minimize contamination of the body kinematics by the wingbeat.

Figure 4.

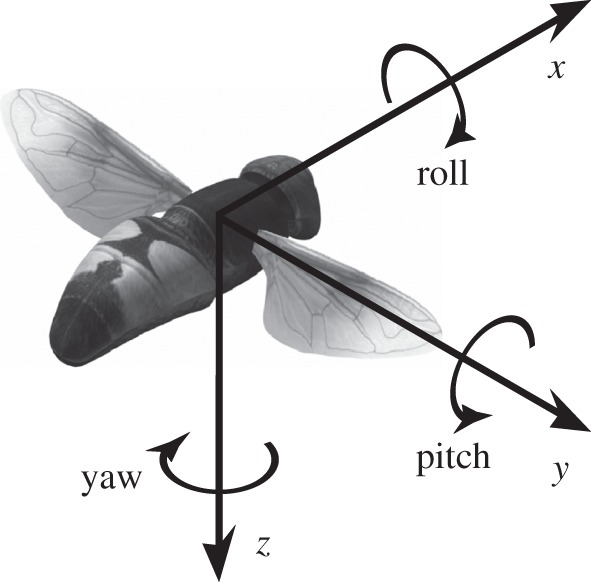
Right-handed body-fixed axis system. The axis system is centred on the centre of volume of the body, including the head. The x-axis is defined as the long axis of the body, calculated using principal components analysis. The y-axis is parallel to the line joining the two wing bases. Pitch, roll and yaw are signed positive in the directions of the curved arrows. Angular accelerations about the pitch axis, and linear accelerations along the x- and y-axes are expected to be correlated with symmetric changes in the wing kinematics. Angular accelerations in roll and yaw, and linear acceleration along the y-axis are expected to be correlated with asymmetric changes in the wing kinematics.

We used our quintic splines to calculate the linear velocity and Euler angle rates of the body in laboratory coordinates, and transformed these to obtain the linear velocity and angular velocity with respect to the body axes [24]. Positive angular velocity about the x-axis indicates roll to the right; positive angular velocity about the y-axis indicates nose-up pitching motion; positive angular velocity about the z-axis indicates yaw to the right (figure 4). We then used central finite differences to estimate the linear and angular accelerations with respect to the body axes, although as the body is rotating, these are not equivalent to the total acceleration experienced by the insect [24]. Note that negative accelerations do not necessarily imply a slowing down of the insect; for instance, a large negative acceleration in the x-axis can also result if a hoverfly is flying backwards at an increasing speed.

2.4. Measurement of wing kinematics

We define all of the wing kinematic parameters with respect to the stoke plane, rather than with respect to the body axes. For each half stroke, the stroke plane is defined as the plane including the position of the wing base and the position of the wing tip at each stroke reversal. The stroke plane angle is defined as the inclination of this plane with respect to the long axis of the body, and is signed positive when the stroke plane tilts nose-down.

The motion of the wing is not strictly planar; so the instantaneous position of the wing tip is defined relative to the wing base by a pair of spherical coordinates. These spherical coordinates are known as the stroke angle (measured within the stroke plane) and the deviation angle (measured normal to the stroke plane). Stroke angle is signed positive when the wing tip is anterior to the wing base (figure 5a); the deviation angle is signed positive when the wing tip is dorsal to the wing base (figure 5b).

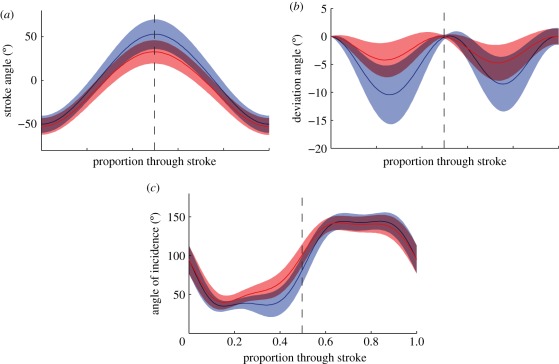
Figure 5.

Definition sketches of the measured wing kinematic variables that vary through a stroke. The measurements were made in a right-angled, body-fixed axis system (x′y′z′) with its origin at the wing base. The x′y′-plane is defined by the stroke plane, with the x′-axis pointing forward within the plane of symmetry of the insect, and the z′-axis pointing down. (a) The stroke angle (φ) is defined as the angle between the line joining the wing tip and wing root and its projection onto the stroke plane. (b) The deviation angle (θ) is measured orthogonal to the stroke angle, and is defined as the angle between the line joining the wing tip and wing root and its projection onto the stroke plane. (c) The angle of incidence (α) is defined as the angle between the line joining the leading and trailing edge of the wing and its projection onto the stroke plane. The angle of incidence is measured in the x_wz′-plane, in which the x_w-axis lies on the stroke plane, and is perpendicular to the long axis of the wing.

The local angle of incidence is defined at any location along the wing as the angle between the line joining the wing leading and trailing edge, and the projection of this line onto the stroke plane (figure 5c). This angle is always measured relative to the anatomical ventral surface of the wing, and so is normally less than 90° on the downstroke and greater than 90° on the upstroke. We also summarized the changes in angle of incidence along the wing by estimating the linear component of the twist distribution from the regression of angle of incidence against distance along the wing.

The stroke angle, deviation angle and local angle of incidence vary continuously through the stroke but summary measurements can be defined for each of these variables on every half stroke. The stroke amplitude is defined as the absolute difference in stroke angle between the two extremes of each half stroke. The timings of supination and pronation were defined as the times at which the angle of incidence halfway along the wing reached 90° at the end of each downstroke and upstroke. These times were measured relative to the timing of stroke reversal and were normalized by the wingbeat period. Other summary parameters were measured by recording the orientation of the wing at the middle of each half stroke. We used this to define the mid-stroke stroke angle, mid-stroke deviation angle, mid-stroke twist distribution and mid-stroke angle of incidence (measured halfway along the wing).

2.5. Measurement of alula state

The alula itself could not be tracked automatically because its proximity to the body meant that it was partially occluded from view at certain stages of the stroke. Earlier analysis had shown that the state of the alula could be categorized in a binary fashion [12]. The state of the alula is most apparent at mid-upstroke, and we therefore recorded the state of the alula at mid-upstroke, according to whether it was flipped or flat with respect to the rest of the wing. We did this manually for every wingbeat, to give a dataset totalling 26 236 wingbeats for which we had measurements of body kinematics, wing kinematics and alula state.

The wing and body kinematics data that we collected in this study were optimized for investigating complete flight manoeuvres and are therefore at slightly lower spatial resolution than wing kinematic data that we have collected previously for single wingbeats [12]. In order to investigate the kinematics of the alula itself in the greatest possible detail, we additionally analysed the motion of the alula with respect to the wing for a different dataset for E. tenax, previously described in Walker et al. ([12]; 43 wingbeats from six individuals). We used manual tracking to measure the angle of the alula relative to the wing chord at 25 per cent of wing length, signing the angle positive when the alula was deflected dorsally with respect to the wing.

2.6. Microscopic examination of the alula

In order to investigate the anatomy and mechanics of the alula and its connection to the wing hinge, we examined two E. tenax under a light microscope, having first anaesthetized them using CO₂ and cooling. The insects were pinned through the wings and thorax with the wings in a position similar to that adopted at mid-downstroke. We manipulated the alula hinge and third axillary sclerite using a seeker to investigate the operation of the alula.

3. Results

3.1. Wing kinematics and alula state

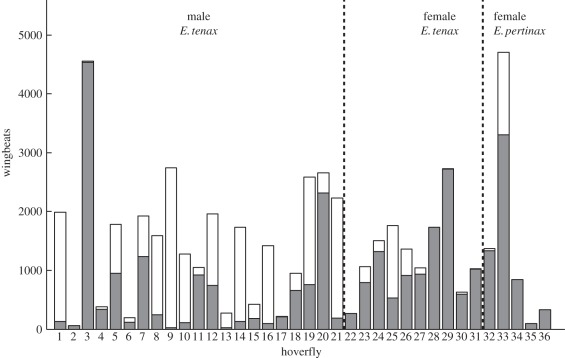
In total, the alula was flipped in 41.4 per cent of the 26 236 recorded wingbeats, combining results from the left and right wings to give n = 52 472 (figure 6). We conclude from this that flipping of the alula is not merely an occasional feature of extreme manoeuvres, but is routine during normal flight. The proportion of wingbeats in which the alula was flipped varied markedly between individuals: in some individuals, the alula was flipped on almost every wingbeat, while there were five hoverflies that did not flip their alula on any wingbeat. These five individuals were all engaged in fast forward flight, and had comparatively few recorded wingbeats. Flipping of the alula was most common in male E. tenax, which might reflect reported differences in flight behaviour between the sexes, such as the greater proportion of time spent in hovering or chasing behaviours in males [16]. However, we observed no obvious qualitative differences in the general flight of males and females in the flight arena.

Figure 6.

Number of wingbeats and frequency of alula flipping for n = 36 hoverflies. The height of the bars indicates the total number of wingbeats measured for each individual, treating measurements for the left and right wings as separate datapoints in this figure. The lower, shaded part of each bar shows the number of wingbeats where the alula was flat; the upper, unshaded part of the bar indicates wingbeats where the alula was flipped. All of the hoverflies had wingbeats where the alula was flat; only five hoverflies did not have the alula flipped on any wingbeats.

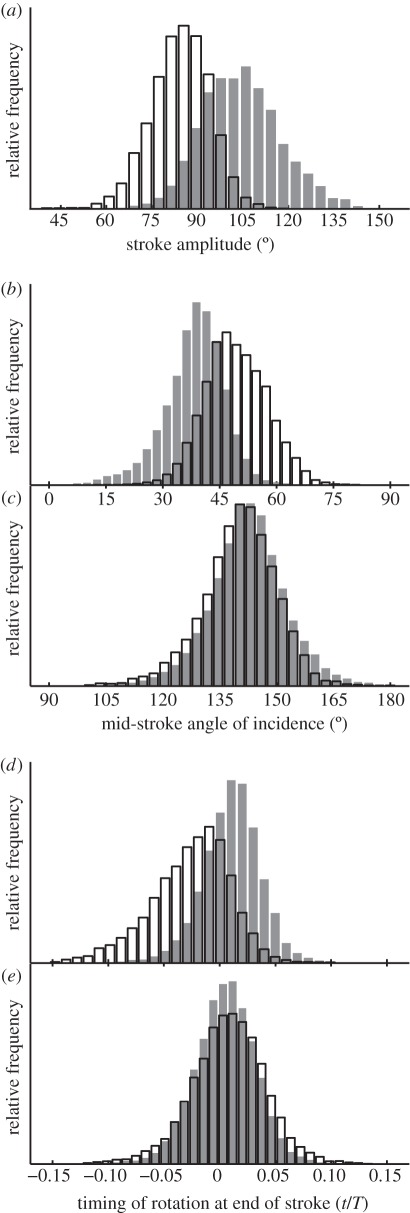
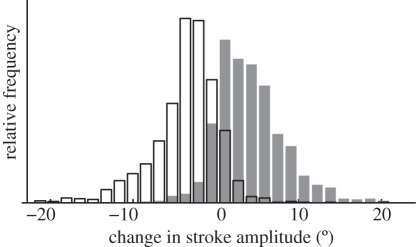
There are obvious differences in the distribution of several of the summary wing kinematic parameters when the data for each wing are categorized according to whether the alula was flipped or flat. These differences are most apparent in respect of stroke amplitude. For example, the mean stroke amplitude is 14° lower on the downstroke when the alula is flipped, compared with when the alula is flat (figure 7a); a similar pattern is observed on the upstroke. Stroke amplitudes greater than 120° were only ever observed when the alula was flat, while amplitudes less than 70° occurred only when the alula was flipped. This implies that the state of the alula indicates some change in the physical apparatus of the wing hinge that limits stroke amplitude. This conclusion is strengthened by considering only the subset of wingbeats in which the alula changes state from one wingbeat to the next: when the alula changes state from flat to flipped, there is usually an accompanying decrease in the stroke amplitude from one wingbeat to the next (figure 8). The opposite change in stroke amplitude is observed when the alula changes state from flipped to flat. Most of the wing kinematic parameters varied similarly according to the state of the alula on both the downstroke and upstroke. However, the mid-stroke angle of incidence and the timing of rotation at the end of the half stroke only showed an effect on the donwstroke (figure 7b–e).

Figure 7.

Histograms showing how the distributions of several key wing kinematic parameters are associated with the state of the alula. The data have been categorized according to the state of the alula; flat (shaded bars) or flipped (unshaded bars) and pools data from the left and right wings. (a) Downstroke stroke amplitude; (b) mid-downstroke angle of incidence; (c) mid-upstroke angle of incidence; (d) timing of supination at the end of the downstroke; (e) timing of pronation at the end of the upstroke. The timing of rotation is expressed as a fraction of the total stroke period (t/T), and is measured relative to the timing of stroke reversal.

Figure 8.

Histogram showing how the distribution of change in stroke amplitude between consecutive wingbeats is associated with the change in state of the alula. The bars are shaded according to how the alula changes state over two wingbeats; flipped to flat (shaded) or flat to flipped (unshaded) and pools data from the left and right wings.

Data from the left and right wings are highly correlated; so in testing for the statistical significance of these effects, we took the mean for both wings and categorized the data into three groups: both alulae flipped; both alulae flat; one alula flipped and the other alula flat. Statistical analyses of these time-series data are also confounded by autocorrelation. For example, a hoverfly with a high stroke amplitude on one wingbeat would usually have a high stroke amplitude on the next. We therefore used a first-order autoregressive model [25] to test whether the mean of each of the summary wing kinematic parameters varied according to the state of the alula, controlling for video sequence number in the model. The autoregressive model includes an additional parameter that attempts to control for the effects of autocorrelation [26], which we estimated using a maximum-likelihood method. Testing the statistical significance of the autoregressions independently for each of the 16 summary wing kinematic parameters greatly inflates the overall risk of falsely rejecting a true null hypothesis (i.e. committing a type I error). We therefore used a false discovery rate method to control the expected proportion of false positives at the 5 per cent level in determining whether a particular variable was significant [27].

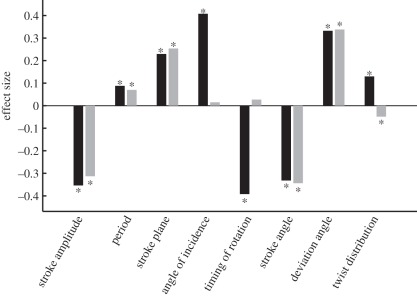
The autoregressive models indicated that 14 of the 16 parameters were significantly associated with the alula state, after correcting for the false discovery rate (table 1). Only the mid-upstroke angle of incidence and the timing of pronation at the end of the upstroke were not significantly associated with the state of the alula. We calculated the effect size for each wing kinematic parameter by dividing the difference in the model coefficients for cases where the alulae were both flipped or both flat by the standard deviation of the parameter (figure 9). Although most of the parameters were significantly associated with the alula, the effect size varied considerably. Stroke amplitude, mid-downstroke angle of incidence, timing of supination, mid-stroke stroke angle and mid-stroke deviation angle had the largest effect sizes, while stroke period, wing twist distribution and stroke plane had comparatively smaller effect sizes.

Table 1.

Summary of the results of the 16 first-order autoregressive models used to determine whether each of the eight summary wing kinematic parameters for the downstroke and the upstroke are associated with the state of the alula on each wingbeat (both flipped, both flat, one flipped and one flat). For each wing kinematic parameter, the mean value for both wings was used as the response variable in a first-order autoregressive model controlling for video sequence number. The F-statistics and associated p-values are calculated using sums of squares adjusted for the other terms in the model (i.e. type III sums of squares). The p-values give the probability of observing an F-statistic as large or larger than that which was observed, under the null hypothesis of no association [25]. Because we have quoted 16 separate p-values, using the frequentist approach of treating those that are less than 0.05 as significant would result in an inflated overall risk of type I error. We therefore used a false discovery rate method to control the expected proportion of false positives at the 5% level [27]. Of the 16 parameters, 14 were significantly associated with alula state, after controlling the overall false discovery rate (see text). Significant associations are shown in bold.

wing kinematic parameters	downstroke		upstroke
	p	F2,25 358	p	F2,25 358
stroke amplitude	<0.001	766	<0.001	530
stroke period	<0.001	52.5	<0.001	31.0
stroke plane	<0.001	248	<0.001	244
mid-stroke angle of incidence	<0.001	365	0.667	0.40
timing of rotation at end of stroke	<0.001	318	0.050	3.01
mid-stroke stroke angle	<0.001	519	<0.001	544
mid-stroke deviation angle	<0.001	426	<0.001	227
mid-stroke twist distribution	<0.001	16.5	<0.001	4.62

Figure 9.

Size of the effect of alula state on the various wing kinematic parameters. The effect size is calculated as the difference between the regression coefficients for cases where the alulae were both flipped or both flat, normalized by the standard deviation of the parameter. The bars are shaded to indicate half stroke; downstroke (black); upstroke (grey). The asterisks above or below the bars indicate which parameters were significantly associated with the alula, after controlling the false discovery rate (see also table 1).

The changes in the wing kinematics observed through the wingbeat provide further insight into how the wing kinematics vary according to the state of the alula. Stroke angle, deviation angle and angle of incidence all show clear differences at certain stages of the wingbeat according to the state of the alula (figure 10). The stroke reversal at the end of the downstroke occurred at a reduced stroke angle when the alula was flipped, whereas the stroke reversal at the end of the upstroke occurred at approximately the same angle, regardless of the state of the alula (figure 10a). This explains the reduction in stroke amplitude and decrease in mid-stroke stroke angles seen in the summary wing kinematic parameters in figure 9. The deviation angle is defined to be zero at the start of each half stroke, but for the rest of the wingbeat, there is an increase in the deviation angle when the alula is flipped, resulting in a flatter wing tip path, lying closer to the stroke plane (figure 10b). The mid-span angle of incidence shows less of a difference according to the state of the alula, but when the alula is flipped there is a noticeable increase in the angle of incidence from mid-downstroke through to early upstroke (figure 10c).

Figure 10.

Changes in wing kinematics through time. (a) Stroke angle; (b) stroke deviation angle; (c) mid-span angle of incidence. The data are categorized according to the state of the alula: flipped (red line); flat (blue line). The shaded region around each line indicates one standard deviation.

3.2. Association between body kinematics and alula state

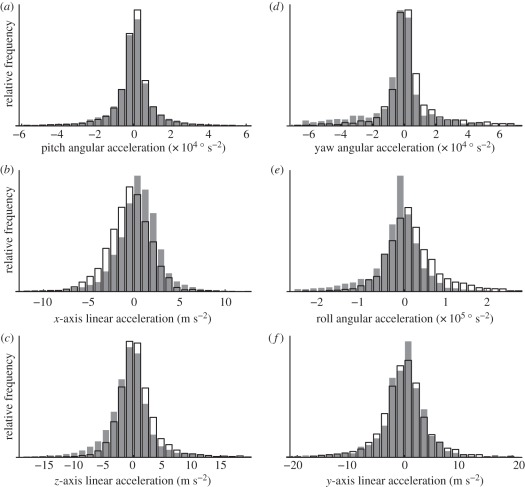
Symmetric angular accelerations of the body about the pitch axis, and symmetric linear accelerations of the body along the x- or z-axes (figure 4), are all expected to be correlated with symmetric changes in the wing kinematics. Asymmetric angular accelerations about the yaw or roll axes, and asymmetric linear accelerations along the y-axis (figure 4), are all expected to be correlated with asymmetric changes in the wing kinematics. Figure 11a–c compares the pitch, x- and z-axes accelerations for wingbeats when the alulae were flat on both wings, or flipped on both wings. Figure 11d–f compares the yaw, roll and y-axis accelerations for wingbeats where the alula was flipped on only the left or the right wing. The distributions of several of these body kinematic parameters vary according to the state of the alulae, most noticeably the acceleration along the x-axis (figure 11b) and roll angular acceleration (figure 11e), although the effect sizes are small compared with those observed for the wing kinematics (figure 7).

Figure 11.

Histograms showing how the distributions of the body kinematic parameters are associated with the state of the alula. (a–c) Symmetric body accelerations; (d–f) asymmetric body accelerations. The data have been categorized according to the state of both alulae: (a–c) either both flat (shaded) or both flipped (unshaded); (d–f) either left alula flipped and right alula flat (shaded) or right alula flipped and left alula flat (unshaded).

In order to analyse statistically the effects of the alula upon symmetric body accelerations, we categorized the data into the following groups: both alulae flipped; both alulae flat; one alula flipped and the other alula flat. For analysing asymmetric accelerations, we categorized the data as follows: left alula flipped and right alula flat; right alula flipped and left alula flat; both alulae in the same state. The data were analysed using the same autoregressive model as for the wing kinematics (§3.1), once again controlling the false discovery rate at the 5 per cent level (table 2). Symmetric flipping of the alulae was associated with decreased acceleration along the x-axis (figure 11b), and increased acceleration along the z-axis (figure 11c), but was not associated with any difference in pitch acceleration (figure 11a). Because the z-axis points downward (figure 4), the differences in linear acceleration associated with flipping of the alulae are both indicative of a reduction in the flight forces produced by the insect. Asymmetric flipping of the alulae was associated with yaw and roll angular accelerations, but not with linear acceleration along the y-axis (table 2). Both the roll and yaw accelerations increased in the direction of the flipped alula (figure 11d,e), which is again suggestive of a decrease in force production of the wing with the flipped alula.

Table 2.

Summary of the results of the six first-order autoregressive models used to determine whether each of the body kinematic parameters is associated with the state of the alula. For symmetric accelerations, we categorized the data into the following groups: both alulae flipped; both alulae flat; one alula flipped and the other alula flat. For analysing asymmetric accelerations, we categorized the data as follows: left alula flipped and right alula flat; right alula flipped and left alula flat; both alulae in the same state. We controlled for video sequence number in fitting the model. The F-statistics and associated p-values are calculated using sums of squares adjusted for the other terms in the model (i.e. type III sums of squares). Of the six parameters, four were significantly associated with alula state, after controlling the overall false discovery rate at the 5% level (see text and legend to table 1 for further explanation). Significant associations are shown in bold.

body acceleration	p	F2,25 358
pitch angular acceleration	0.098	2.33
x-axis linear acceleration	<0.001	43.8
z-axis linear acceleration	<0.001	21.6
yaw angular acceleration	<0.001	48.9
roll angular acceleration	<0.001	175.1
y-axis linear acceleration	0.211	1.56

3.3. Alula kinematics

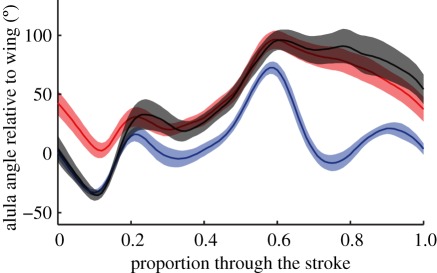
In order to investigate the detailed kinematics of the alula, we analysed the motion of the alula with respect to the wing for a higher resolution dataset for E. tenax, previously described in Walker et al. [12]. The alula rotates continuously relative to the rest of the wing, and momentarily passes through angles as high as 70° even on wingbeats during which it is not flipped owing to inertial forces (figure 12, black line). The alula reaches angles greater than 90° on wingbeats during which it is flipped (figure 12, red line), and this high angle is sustained through much of the upstroke following supination (figure 12, compare red line with black line). Although the difference between the two states of the alula becomes most pronounced at supination, the transition between states appears to occur at mid-downstroke. The blue line in figure 12 represents wingbeats for which the alula was not flipped, and had not been flipped on the preceding wingbeat. The red line represents wingbeats for which the alula was flipped, and had been flipped on the preceding wingbeat. The black line represents wingbeats for which the alula was flipped, but had not been flipped on the previous wingbeat. The shaded area around each line denotes the width of the 95% confidence interval for the mean. The black line is statistically indistinguishable from the blue line at the start of the downstroke, but changes so that it is statistically indistinguishable from the red line by the middle of the downstroke. This, then, is the moment at which the alula switches from one state to the other. A corollary of this conclusion is that the angle of the alula during the first part of the downstroke depends upon whether it was flipped or flat during the preceding upstroke. Our treatment of the alula as a binary variable, classified based on its state during the upstroke, is also justified by these results.

Figure 12.

Mean and 95% CI of the angle of the alula relative to the angle of the wing at 25% wing length through the course of the wingbeat for Eristalis tenax. The lines are coloured according to the state of the alula on the current and previous wingbeat: blue line, flat on the previous and current wingbeat (n = 37); red line, flipped on the previous and current wingbeat (n = 32); black line, alula flat on the previous wingbeat, but flipped on the current wingbeat (n = 17). The alula reaches angles greater than 90° when the alula is flipped and this high angle in maintained for much of the upstroke. The alula apparently transitions from the flat to flipped state at mid-downstroke, when the black line switches between the blue line and the red line.

3.4. Actuation of the alula

The alula is deflected upwards when the wings are held in their resting position over the thorax and abdomen (figure 13). The third axillary sclerite is the main sclerite involved in wing retraction, and microscopic examination of the alula hinge reveals that there is a clear connection between the alula and the third axillary sclerite (figure 3). The main hinge line connecting the alula to the rest of the wing is extremely flexible and malleable but the alula itself is non-planar and has concave curvature, providing natural rigidity. The proximal region of the alula cuticle is folded upon itself to form a raised protrusion. The third axillary sclerite is fused to a sclerotized region of the second anal vein and a flexible section of cuticle extends from this fused joint to form a socket for the raised protrusion of the alula. Manipulation of the flexible cuticle complex causes the alula to rotate about the flexible hinge and to flip up, with only minimal force required to achieve the effect. There is no evidence that the alula is bistable, and instead its flipped position appears to be maintained through the constant application of force by the third axillary sclerite.

Figure 13.

Photograph of Eristalis tenax with the wing positioned when the insect is at rest. The alula (Al) is flipped so that it does not impede the retraction of the wing over the thorax and abdomen. S2, sclerotized extension from third axillary sclerite; A2, second anal vein; F, flexible section of cuticle that forms socket with raised protrusion of the alula (dotted line).

4. Discussion

4.1. Operation of the alula

We have shown that the state of the alula is associated with pronounced differences in the distribution of several key wing kinematic parameters, including stroke amplitude, stroke deviation angle, mid-downstroke angle of incidence and timing of supination (figure 9). Although the distributions of these parameters overlap for the two states of the alula, the tails of the distributions do not overlap, such that very high or very low values of the key parameters are always associated with one or other state of the alula (figure 7). Changes in the state of the alula from one wingbeat to the next are also associated with immediate changes in the wing kinematics: on average, stroke amplitude decreases by 6.8° between wingbeats when the alula changes state from flat to flipped (figure 8). We expect these differences in wing kinematics to be associated with differences in the aerodynamic forces; so it is not surprising that the state of the alula also predicts aspects of the body dynamics (figure 11). In general, flipping of the alula seems to be associated with reduced aerodynamic force production. The alula itself is actuated by the third axillary sclerite (figure 3). We therefore conclude that changes in the state of the alula indicate changes in flight mode in hoverflies, involving movements of the third axillary sclerite.

The alula itself is a prominent feature of the wings of most brachyceran flies, and accounts for up to 10 per cent of the wing surface in hoverflies (figure 2). Nevertheless, it has received scant attention in the biomechanics literature, typically being noted only as an anatomical feature [28]. Weis-Fogh [29] briefly mentioned flipping of the alula in hoverflies, and hypothesized that as it was controlled by means of an axillary muscle it might therefore be used for yaw control. However, the proximal part of the wing where the alula is located generates minimal aerodynamic force in hovering or slow forwards flight, because its relative velocity is low [30]. It therefore seems likely that any aerodynamic function of the alula will only be realized in fast forward flight, when the relative velocity of the wing base is comparatively high. Fast forward flight is characterized by high stroke amplitude, and under such conditions, the alula is held flat to the wing (§3.1; figure 7a). We therefore propose that the primary aerodynamic function of the alula is to increase the surface area of the wing during fast forward flight, and that its hinged design is important in allowing the wings to be held over the thorax and abdomen when the insect is at rest (figure 13). We suggest that the alula is flipped during flight manoeuvres, not necessarily for any aerodynamic reason, but rather because the third axillary sclerite that actuates it for the purposes of wing retraction is also involved in flight control.

4.2. The alula and gear change in flies

One possible mechanism for the changes in flight mode that we have observed in Eristalis is the so-called gear change mechanism of flies. Most previous work on gear change has been done with Calliphora [1,4,7,8], and interspecific differences in the detailed morphology of the wing hinge lead us to expect that there will also be interspecific differences in the operation of the gear change mechanism. In particular, the presence of only one notch on the pleural wing process of Eristalis [2] suggests that there might only be two possibilities for its interaction with the radial stop: engaged or disengaged (figure 1). We therefore predict that there might only be two principal gears in this species, when compared with the three that are thought to exist in Calliphora [1]. Nevertheless, it is reasonable to use the information on gear change that is available from Calliphora to test whether a similar gear change mechanism might be associated with the different flight modes linked with the two states of the alula in Eristalis.

The involvement of the third axillary sclerite in gear change in Calliphora is supported by kinematic and electrophysiological evidence [1,8]. We have shown that small movements of this sclerite cause flipping of the alula (figure 3) and have also shown that the state of the alula is associated with differences in the observed distributions of wing and body kinematics in Eristalis. Although there are distinct shifts in the distribution of the parameters according to the state of the alula, there still remains a large overlap between the respective distributions. This is to be expected considering the action of the steering muscles at the wing hinge: the first and third axillary muscles control the modes in the gear change mechanism, but the basalar muscles modify the wing kinematics within the modes [8]. In the remainder of this section, we show that the specific differences in wing kinematics that we have observed, and the detailed timing with which they occur, are consistent with almost all of the properties of the gear change mechanism that have been reported previously for Calliphora (table 3).

Table 3.

Summary of the similarities between the alula flipping and the gear change mechanism in Diptera.

alula flipping	gear change mechanism
controlled by 3rd axillary sclerite	involves movement of 3rd axillary sclerite[1]
changes state at mid-downstroke	comes into effect at mid-downstroke[1]
highly variable amongst individuals	highly variable among individuals[1]
associated with large changes in the distribution of wing kinematic parameters	associated with large changes in the distribution of wing kinematic parameters[1,8]
associated with reduced stroke amplitude	associated with reduced stroke amplitude[1,8]
associated with earlier supination	associated with delayed supination[1]
associated with body manoeuvres	associated with body manoeuvres[1]

Nalbach [1] reported that the frequency with which different gears were used by tethered Calliphora was extremely variable among individuals, with some never engaging the radial stop with the pleural wing process (figure 1). This is true also of the frequency of alula flipping in Eristalis (figure 6). It is unclear why such differences between individuals occur: with the exception of a few hoverflies that consistently flew at high forward speed with high stroke amplitude and with the alula flat, there were no clear qualitative differences in flight behaviour between those hoverflies that had their alulae flipped for most wingbeats and those that had them flat. This intrinsic variability in flight behaviour highlights the importance of using large sample sizes when investigating insect wing kinematics, and may explain some of the inconsistencies that exist between the results of different workers studying the wing hinge (Sarcophaga [2]; Calliphora, Eristalis, Tipula [6]; Calliphora [1]).

The gear change mechanism has already been correlated with changes in certain wing kinematic parameters, particularly stroke amplitude and deviation angle (Calliphora [1,8]). When the radial stop and pleural wing process are engaged, a reduction in the stroke angle at the end of the downstroke results in reduced stroke amplitude: we have found precisely the same result in conjunction with flipping of the alula (figure 10a). The stroke deviation angle is also increased relative to the stroke plane when the alula is flipped, resulting in a more nearly planar wing tip trajectory (figure 10b). Similar changes in stroke deviation angle are associated with changes in the firing pattern of the muscles actuating the third axillary sclerite, which have been explicitly attributed to gear change [8]. These effects are observed on both the downstroke and the upstroke, which is not surprising because the end of one downstroke is the start of the next upstroke, and both measurements therefore share information between consecutive half strokes.

Nalbach [1] found that when the radial stop and pleural wing process were engaged in Calliphora, there was a qualitative delay in the timing of supination, measured as the time when the wing rotates past 90° relative to the stroke plane. In our measurements with Eristalis, we found that supination occurred earlier when the alula was flipped (figure 7d and table 1). It is unclear why the direction of this effect should be different between our results and those of Nalbach [1], especially given the consistency in other respects, but it may be that subtle differences in the morphology of the wing hinge between Calliphora and Eristalis account for this [2]. In addition, whereas our insects were observed in free flight, Nalbach's data were collected in tethered flight, which may elicit different behaviours [1]. In any case, it is clear that changes in the timing of supination are associated with both flipping of the alula and with gear change.

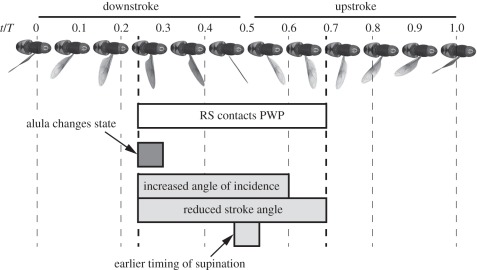
If we examine the precise timing of changes in the wingbeat kinematic parameters that we have observed, then a consistent picture emerges (figure 14). Nalbach [1] found that the radial stop contacts the pleural wing process in certain flight gears, and observed that this contact occurred from mid-downstroke through to early upstroke in Calliphora: the alula also changes state at mid-downstroke (figures 12 and 14). Furthermore, it is possible to explain all of the associated changes in the summary wing kinematic parameters in terms of changes in wing trajectory that occur during the same phase of the stroke. Specifically, these changes can be attributed to differences in the position of the wing tip at the end of the downstroke, and to differences in the angle of incidence of the wing from mid-downstroke to early upstroke. For example, when the alula is flipped, there is a decrease in stroke angle at the end of the downstroke. This obviously results in a reduction in stroke amplitude and mid-downstroke stroke angle, but will also result in an increase in stroke deviation angle and stroke plane angle, on account of the curvature of the wing tip trajectory (figure 15).

Figure 14.

Timeline of the wingbeat of Eristalis, showing the similarities in the gear change mechanism measured by Nalbach [1] for Calliphora and the changes in alula state and wing kinematic measurements presented here. During the wingbeat, the gear change comes into effect when the radial stop (RS) contacts the pleural wing process (PWP) at mid-downstroke, and lasts until early upstroke. The alula changes state at the same time as the radial stop contacts the pleural wing process. This is also the time at which the angle of incidence and stroke angle change according to the state of the alula. The timing of supination is also altered, but the timing of pronation is outside the window where the gear change mechanism operates, and so is unaffected.

Figure 15.

Illustration of how the position of the wing tip at the end of the downstroke affects wing kinematic parameters. The wing tip trajectory (solid line) typically follows a shallow curved path. The stroke plane (dashed line) is defined by the line joining the positions wing tip at each half stroke reversal. (a) Large stroke amplitude, with horizontal stroke plane. (b) Reduced stroke angle of the end of the downstroke results in a decrease in stroke amplitude and mid-stroke stroke angle, but also an increase in stroke plane angle and deviation angle owing to the flatter wing tip path relative to the stroke plane.

It is at least as important to note that two wing kinematic parameters were not significantly associated with alula state, namely the mid-upstroke angle of incidence and the timing of pronation at the end of the upstroke (figure 7c,e and table 1). The timing of the interaction between the pleural wing process and the radial stop provides a straightforward explanation of why these two parameters are not associated with the state of the alula (figure 14). If the radial stop contacts the pleural wing process, then it does so from mid-downstroke through to early upstroke (Calliphora [1]). The timing of pronation and the mid-upstroke angle of incidence are measured outside this time period and they are therefore not affected by the gear change mechanism.

If gear changes have any functional significance, then we would expect to see differences in body kinematics associated with gear changes, and hence with changes in the state of the alula. Nalbach [1] noted that radial stop and pleural wing process were most commonly engaged on the inner wing during fictive turns in tethered Calliphora. The state of the alula is significantly associated with accelerations in four of the body's six degrees of freedom; x- and z-axes linear acceleration, and yaw and roll angular acceleration (figure 11 and table 2). During asymmetric manoeuvres, the alula was typically flipped on the inner wing, while during symmetric manoeuvres the flipping of both alulae was associated with backward or downward acceleration. In each case, the direction of the effect is consistent with there being a reduction in the aerodynamic forces on a wing when the alula is flipped.

We have already established that the aerodynamic effects of the alula are likely to be small in hovering or slow forward flight [30]. We therefore hypothesize that the observed changes in the aerodynamic forces are due to associated changes in wing kinematics, rather than to the aerodynamic effects of the alula. Stroke amplitude is certainly a key factor in determining aerodynamic force [9,11], and its reduction when the alula is flipped would produce the expected changes in the aerodynamic forces and body kinematics. Other wing kinematic parameters are almost certainly important too, but it is difficult to ascertain their relative contribution to the aerodynamic forces, particularly as changes in these parameters are all highly coupled.

Neither pitch angular accelerations nor y-axis linear accelerations were significantly associated with the alula state. Decreasing stroke amplitude, by reducing the stroke angle at tip reversal at the end of the downstroke, should cause the flight force to shift back, generating a pitch down acceleration [9], but it is possible that such effects may be negated by the other change in the wing kinematics, in particular the changes in angle of incidence and the timing of supination, which are also important in flight control [31,32]. Diptera typically have little control over sideslip forces, with respect to the body [33]; so it is unsurprising that the gear change mechanism would produce no noticeable change in the y-axis accelerations.

4.3. Functional significance of flight modes

There is an increasing body of evidence to support the notion that Diptera use different modes of wing kinematics to enable different modes of flight [1,8,15,16,34]. In Eristalis, at least, it appears that the state of the alula acts as an indicator of flight mode, and more specifically may reveal the action of the gear change mechanism. Our data suggest that gear change is routinely used by Eristalis in the course of the manoeuvres they execute in normal free flight. Gear change might also have useful implications for elastic storage, by altering which components of the wing hinge absorb energy at the end of the downstoke [1]. Perhaps more importantly, the gear change mechanism may allow flies to switch rapidly from one set of kinematics to another between consecutive wingbeats, and might well be associated with the generation of saccades. Fast saccadic manoeuvres are characteristic of the flight of most flies, and the ability to switch quickly between different flight modes would be of particular ecological relevance to hoverflies such as Eristalis that hover to defend territories and therefore need to switch rapidly to high accelerations to intercept intruders or potential mates.