Figure 1.

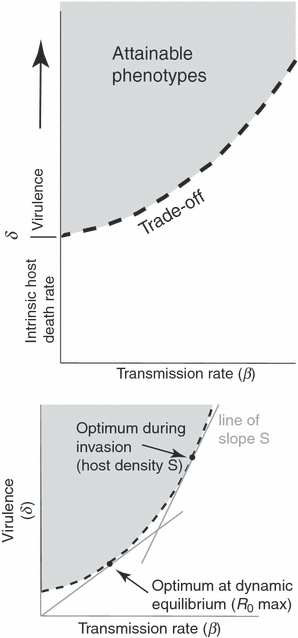
(Top) Death rate of infected hosts (δ) in relation to transmission (β). Death rate is divided into intrinsic host death rate and virulence – parasite-induced host death rate. The intrinsic host death rate is assumed to be constant, so the virulence-transmission trade-off (dashed curve) emanates from the axis at this value and increases as transmission increases. The trade-off gives the minimum total parasite death rate (δ) that could be achieved for a given transmission rate (β), so only points on and above the trade-off boundary are attainable by the parasite (shaded). For simplicity, we henceforth refer to δ as virulence, but acknowledge that it is the sum of a constant mortality plus virulence. (Bottom) Optimum for a parasite invading a host population, when the susceptible host density remains constant at S. During the epidemic phase, the parasite’s optimum lies on the dashed trade-off function and satisfies the condition that the slope of the tangent along the trade-off function equals the current density of hosts, S (upper arrow). As the parasite epidemic reduces the density of susceptible hosts, the optimum shifts progressively further down the trade-off curve, until dynamic equilibrium is reached, whereby parasite and host densities remain constant. In this state, the parasite optimum maximizes R₀ = β/δ, given by the point at which a line through the origin is tangent to the trade-off function (lower arrow). In this paper, we are concerned chiefly with conditions at and shortly after the time of invasion, before the population has reached dynamic equilibrium.