Abstract
Background
The property values of therapeutic gas mixtures are important in designing devices, defining delivery parameters, and in understanding the therapeutic effects. In the medical related literature the vast majority of articles related to gas mixtures report property values only for the pure substances or estimates based on concentration weighted averages. However, if the molecular size or structures of the component gases are very different a more accurate estimate should be considered.
Findings
In this paper estimates based on kinetic theory are provided of density, viscosity, mean free path, thermal conductivity, specific heat at constant pressure, and diffusivity over a range of concentrations of He-O2, Xe-O2, N2O-O2 and N2-O2 mixtures at room (or normal) and body temperature, 20 and 37°C, respectively and at atmospheric pressure.
Conclusions
Property value estimations have been provided for therapeutic gas mixtures and compared to experimental values obtained from the literature where possible.
Introduction
Inhaled therapeutic gases in use today include helium (He) for respiratory treatments, and xenon (Xe) and nitrous oxide (N2O) for anesthesia. For clinical applications these gases are used in the form of mixtures with oxygen in a range of concentrations (typically starting from 20% oxygen (O2) concentration by volume, which is equivalent to a mole fraction of 0.20) so as to maintain adequate oxygenation. Other gases, such as nitric oxide (NO) for pulmonary vascular dilation, are used only in trace amounts.
The property values of therapeutic gas mixtures are important in designing devices, defining delivery parameters, and in understanding the therapeutic effects. Properties of interest include density, viscosity, mean free path, thermal conductivity, specific heat, and diffusivity. In the medical literature the vast majority of articles related to gas mixtures report property values only for the pure substances or estimates based on (volume or molar) concentration weighted averages [1-7]. However, if the molecular size or structures of the component gases are very different a more accurate estimate could be considered [8-10]. For this reason property values of helium and xenon mixtures should be considered for more accurate estimation.
Starting with kinetic theory for molecules treated as hard spheres as a basis, a rich literature has developed regarding the modeling of property values based on first principles and increasing complexity of the molecular interactions; in particular, the attraction and repulsion of molecules as first formulated by Chapman and Enskog [8,9]. The empirically determined Lennard-Jones potential energy function has proved to be a good model for many applications. Extensive measurements of the viscosity of gases using oscillating-disk viscometry have primarily been published by Kestin and his colleagues [11-16]. Other equilibrium and transport properties have been extrapolated from the viscosity measurements using the models described above [8,9]. There also exists limited thermal conductivity data measured using a hot wire method [17].
The objective of this short communication is to give a straightforward reference to the applied scientist, engineer, and medical personnel who perform research with therapeutic gas mixtures. We anticipate that this information will assist both in the design and interpretation of experiments. Estimates of density, viscosity, mean free path, thermal conductivity, specific heat at constant pressure, and diffusivity are provided over a range of concentrations of He-O2, Xe-O2, and N2O-O2 mixtures at room (or normal) and body temperature, 20 and 37°C, respectively and at atmospheric pressure; based on kinetic theory and compared to experimental values obtained from the literature where it is possible. For further comparison N2-O2 mixtures will be included because this mixture makes up the composition of medical air.
Methods
Density
All of the mixtures can be evaluated as ideal gases under the conditions considered. As such the density is based on the state equation as,
| (1) |
where ρmix is the mixture density, p is the pressure, T is the absolute temperature and Rmix is the gas constant defined for the mixture as
| (2) |
In Equation (2) Runiv is the universal gas constant, Xi is the mole fraction of the pure gas component, and MWi is the molecular weight of the pure gas component (32 is the molecular weight for oxygen). The units of Rmix depends on the value chosen for Runiv (e.g., 8314 N-m/kgmol-K).
Viscosity
For viscosity we use a semi-empirical method by Wilke [8] that extends the model for collisions between hard spheres to mixtures.
| (3a) |
| (3b) |
| (3c) |
μi and are the viscosities of the pure gas component and oxygen, respectively. The pure gas viscosity estimates are based on the Lennard-Jones empirical function for the potential:
| (4) |
where r is the distance between the molecules, ε is a characteristic energy of the interaction between molecules and σ is a characteristic diameter, or collision diameter. Equation (5) is a viscosity formula based on the Lennard-Jones parameters in units of kg/s-m derived for monatomic gases that has also been shown to work well for polyatomic gases [8],
| (5) |
where Ωμ is a function of ε. Lennard-Jones parameters are tabulated for common gases [8,9] and for the gases herein in Table 1.
Table 1.
Molecular parameters and Lennard-Jones potential parameters for the pure gas components [9].
| Gas | MW | R (J/kg-K) | σ (Å) | ε/κ (°K) | Ωμ at 20°C |
Ωμ at 37°C |
Atomic Diffusion Volume (Σv) |
|---|---|---|---|---|---|---|---|
| He | 4.003 | 2076.9 | 2.551 | 10.22 | 0.7061 | 0.7004 | 2.67 |
| Xe | 131.3 | 63.3 | 4.047 | 231. | 1.4140 | 1.3798 | 32.7 |
| N2O | 44.02 | 188.9 | 3.828 | 232.4 | 1.4190 | 1.3846 | 35.9 |
| N2 | 28.02 | 296.7 | 3.798 | 71.4 | 0.9697 | 0.9535 | 18.5 |
| O2 | 32.00 | 259.8 | 3.467 | 106.7 | 1.0635 | 1.047 | 16.3 |
Values for Ω have been interpolated from Table B-2 in Bird et al. [8]. κ is the Boltzmann constant.
Mean Free Path
The estimation of mean free path is based on the Chapman-Enskog formulation for hard spheres [18], where the mixture viscosity and density account for the interactions of the different molecules:
| (6) |
The input values are obtained from Equations 1-3.
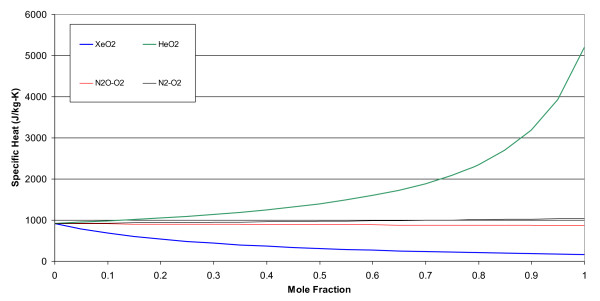
Specific Heat at Constant Pressure
The specific heat at constant pressure (on a per unit mass basis) for all of the mixtures can be evaluated assuming ideal gas behavior and therefore the specific heat curve is a linear function of the mass fraction, though nonlinear in terms of the mole fraction
| (7) |
where and are the specific heats of the mixture and of the pure gas component, respectively. The pure gas values for the monatomic gases are based on the theoretical value The polyatomic estimates are based on empirically derived 4th order polynomials in temperature found in Poling et al. [9].
Thermal Conductivity
Thermal conductivity is treated in an analogous manner to viscosity, where Equation (8a) is equivalent to Equation (3a) and the coefficients are exactly the same based on the pure gas viscosity values.
| (8a) |
| (8b) |
| (8c) |
The pure gas conductivity estimates are based on a modified Eucken approximation found in Poling et al. [9].
| (9) |
Diffusivity
The self diffusivity for a binary system Dij, represents the movement of species i relative to the mixture, where Dij = Dji. The presentation here is based on the method of Fuller et al. given in Poling et al [9], which uses empirically obtained atomic diffusion volumes (Σv).
| (10) |
In Equation (10) j always represents oxygen, the diffusivity is in m2/s, T is the temperature in degrees Kelvin, p is the pressure in bar and the atomic diffusion volumes are given in Table 1 for each gas. is almost independent of composition at low pressures so only a single value will be calculated for each binary gas pair [8].
Of much practical interest is the diffusivity of water vapor or carbon dioxide through the gas mixtures. Values are calculated for these mixtures based on Blanc's law [9].
| (11) |
Where m represents the therapeutic gas mixture considered, j represents the specific therapeutic gas, and k corresponds to H2O or CO2. The diffusion constants in Equation 11 of H2O or CO2 through the therapeutic gas or oxygen are calculated using Equation 10 with atomic diffusion volumes of 13.1 and 26.9 for H2O or CO2, respectively.
Results
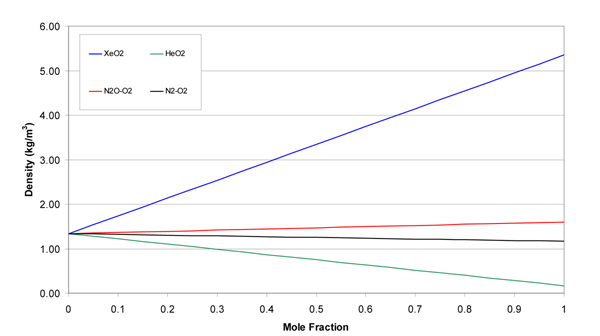
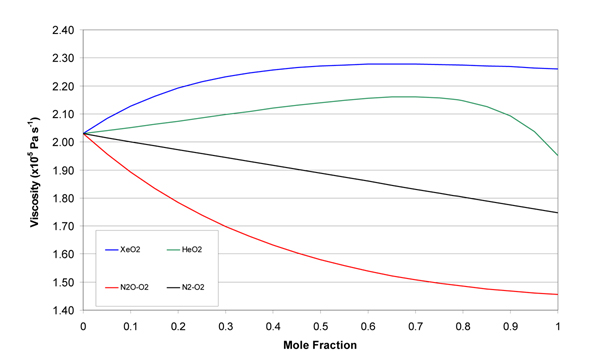
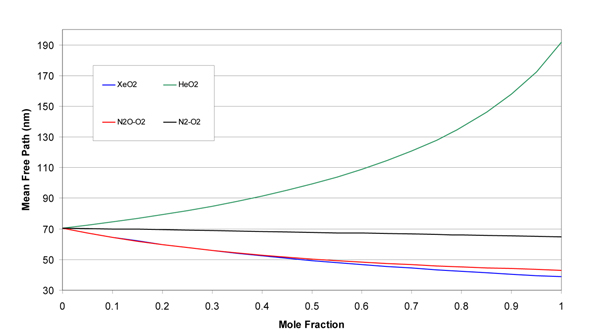
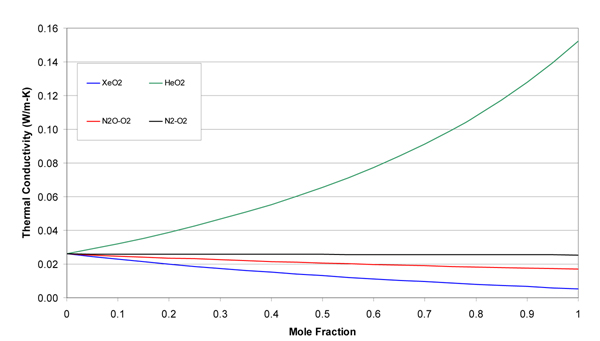
The molecular weights, gas constants, Lennard-Jones parameters, and atomic diffusion volumes for the pure gases are given in Table 1. The mixture results are given in tabular and graphical forms. Tables 2, 3, 4, and 5 give the property values for He, Xe, N2O, and N2 with O2 mixtures, as a function of mole fraction at 20°C. Tables 6, 7, 8, and 9 are the analogous tables for 37°C. Table 10 gives binary diffusivities for the gas mixtures. Figures 1, 2, 3, 4, and 5 are plots of the 20°C data of density, viscosity, mean free path, thermal conductivity, and specific heat, respectively.
Table 2.
He-O2 property values at 20°C and 1 atm.
| He Mole Fraction | ρ (kg/m3) | μ × 105 (kg/s-m) | λ (n m) | k (W/m-K) | cp (J/kg-K) | × 105 (m2/s) | × 105 (m2/s) |
|---|---|---|---|---|---|---|---|
| 0 | 1.330 | 2.029 | 70.561 | 0.026 | 917.5 | 2.551 | 1.573 |
| 0.05 | 1.272 | 2.040 | 72.547 | 0.029 | 945.5 | 2.641 | 1.632 |
| 0.10 | 1.214 | 2.051 | 74.673 | 0.032 | 976.1 | 2.739 | 1.695 |
| 0.15 | 1.156 | 2.063 | 76.954 | 0.035 | 1009.8 | 2.844 | 1.764 |
| 0.20 | 1.098 | 2.074 | 79.409 | 0.039 | 1047.1 | 2.957 | 1.838 |
| 0.25 | 1.039 | 2.086 | 82.057 | 0.043 | 1088.6 | 3.080 | 1.919 |
| 0.30 | 0.981 | 2.097 | 84.924 | 0.047 | 1135.0 | 3.214 | 2.007 |
| 0.35 | 0.923 | 2.109 | 88.038 | 0.051 | 1187.3 | 3.359 | 2.104 |
| 0.40 | 0.865 | 2.120 | 91.432 | 0.055 | 1246.6 | 3.519 | 2.210 |
| 0.45 | 0.807 | 2.131 | 95.148 | 0.060 | 1314.4 | 3.694 | 2.328 |
| 0.50 | 0.748 | 2.141 | 99.235 | 0.066 | 1392.8 | 3.888 | 2.459 |
| 0.55 | 0.690 | 2.149 | 103.751 | 0.071 | 1484.4 | 4.103 | 2.606 |
| 0.60 | 0.632 | 2.156 | 108.773 | 0.077 | 1592.9 | 4.343 | 2.772 |
| 0.65 | 0.574 | 2.161 | 114.393 | 0.084 | 1723.4 | 4.613 | 2.960 |
| 0.70 | 0.516 | 2.162 | 120.735 | 0.091 | 1883.3 | 4.919 | 3.175 |
| 0.75 | 0.457 | 2.158 | 127.959 | 0.099 | 2084.0 | 5.268 | 3.424 |
| 0.78 | 0.422 | 2.152 | 132.807 | 0.104 | 2230.9 | 5.503 | 3.593 |
| 0.79 | 0.411 | 2.150 | 134.522 | 0.106 | 2285.5 | 5.585 | 3.653 |
| 0.80 | 0.399 | 2.147 | 136.291 | 0.108 | 2343.2 | 5.671 | 3.715 |
| 0.85 | 0.341 | 2.127 | 146.059 | 0.117 | 2690.8 | 6.140 | 4.060 |
| 0.90 | 0.283 | 2.092 | 157.788 | 0.128 | 3181.5 | 6.694 | 4.477 |
| 0.95 | 0.225 | 2.037 | 172.409 | 0.139 | 3926.4 | 7.359 | 4.988 |
| 1.0 | 0.166 | 1.952 | 191.912 | 0.152 | 5192.4 | 8.169 | 5.632 |
Table 3.
Xe-O2 property values at 20°C and 1 atm.
| Xe Mole Fraction | ρ (kg/m3) | μ × 105 (kg/s-m) | λ (nm) | k (W/m-K) | cp (J/kg-K) | × 105 (m2/s) | × 105 (m2/s) |
|---|---|---|---|---|---|---|---|
| 0 | 1.330 | 2.029 | 70.561 | 0.026 | 917.5 | 2.551 | 1.573 |
| 0.05 | 1.537 | 2.084 | 67.417 | 0.024 | 782.7 | 2.487 | 1.522 |
| 0.10 | 1.743 | 2.128 | 64.637 | 0.023 | 679.8 | 2.427 | 1.474 |
| 0.15 | 1.950 | 2.163 | 62.138 | 0.021 | 598.6 | 2.369 | 1.429 |
| 0.20 | 2.156 | 2.192 | 59.866 | 0.020 | 533.1 | 2.314 | 1.387 |
| 0.25 | 2.362 | 2.215 | 57.783 | 0.019 | 478.9 | 2.262 | 1.347 |
| 0.30 | 2.569 | 2.232 | 55.863 | 0.017 | 433.5 | 2.211 | 1.309 |
| 0.35 | 2.775 | 2.247 | 54.083 | 0.016 | 394.9 | 2.164 | 1.273 |
| 0.40 | 2.982 | 2.257 | 52.428 | 0.015 | 361.5 | 2.118 | 1.240 |
| 0.45 | 3.188 | 2.265 | 50.883 | 0.014 | 332.5 | 2.074 | 1.208 |
| 0.50 | 3.394 | 2.271 | 49.437 | 0.013 | 307.1 | 2.031 | 1.177 |
| 0.55 | 3.601 | 2.275 | 48.080 | 0.012 | 284.5 | 1.991 | 1.148 |
| 0.60 | 3.807 | 2.277 | 46.804 | 0.011 | 264.4 | 1.952 | 1.121 |
| 0.65 | 4.014 | 2.278 | 45.602 | 0.010 | 246.4 | 1.915 | 1.095 |
| 0.70 | 4.220 | 2.278 | 44.467 | 0.010 | 230.1 | 1.878 | 1.070 |
| 0.75 | 4.427 | 2.276 | 43.395 | 0.009 | 215.3 | 1.844 | 1.046 |
| 0.80 | 4.633 | 2.274 | 42.379 | 0.008 | 201.9 | 1.810 | 1.023 |
| 0.85 | 4.839 | 2.272 | 41.415 | 0.007 | 189.6 | 1.778 | 1.001 |
| 0.90 | 5.046 | 2.268 | 40.500 | 0.007 | 178.3 | 1.747 | 0.980 |
| 0.95 | 5.252 | 2.265 | 39.630 | 0.006 | 167.9 | 1.717 | 0.960 |
| 1.0 | 5.459 | 2.260 | 38.801 | 0.005 | 158.3 | 1.688 | 0.940 |
Table 4.
N2O-O2 property values at 20°C and 1 atm.
| N2O Mole Fraction | ρ (kg/m3) | μx105 (kg/s-m) | λ (nm) | k (W/m-K) | cp (J/kg-K) | × 105 (m2/s) | × 105 (m2/s) |
|---|---|---|---|---|---|---|---|
| 0 | 1.330 | 2.029 | 70.561 | 0.026 | 917.5 | 2.551 | 1.573 |
| 0.05 | 1.355 | 1.956 | 67.394 | 0.025 | 914.3 | 2.500 | 1.542 |
| 0.10 | 1.380 | 1.892 | 64.577 | 0.025 | 911.1 | 2.451 | 1.511 |
| 0.15 | 1.405 | 1.835 | 62.065 | 0.024 | 908.1 | 2.404 | 1.482 |
| 0.20 | 1.430 | 1.784 | 59.820 | 0.024 | 905.2 | 2.358 | 1.454 |
| 0.25 | 1.455 | 1.739 | 57.810 | 0.023 | 902.4 | 2.315 | 1.426 |
| 0.30 | 1.480 | 1.699 | 56.005 | 0.023 | 899.7 | 2.273 | 1.400 |
| 0.35 | 1.505 | 1.664 | 54.383 | 0.022 | 897.1 | 2.232 | 1.375 |
| 0.40 | 1.530 | 1.632 | 52.923 | 0.022 | 894.6 | 2.193 | 1.351 |
| 0.45 | 1.555 | 1.605 | 51.605 | 0.021 | 892.1 | 2.156 | 1.327 |
| 0.50 | 1.580 | 1.580 | 50.414 | 0.021 | 889.7 | 2.119 | 1.305 |
| 0.55 | 1.605 | 1.559 | 49.337 | 0.020 | 887.4 | 2.084 | 1.283 |
| 0.60 | 1.630 | 1.540 | 48.361 | 0.020 | 885.2 | 2.050 | 1.262 |
| 0.65 | 1.655 | 1.523 | 47.475 | 0.019 | 883.0 | 2.017 | 1.241 |
| 0.70 | 1.680 | 1.508 | 46.670 | 0.019 | 880.9 | 1.985 | 1.221 |
| 0.75 | 1.705 | 1.496 | 45.938 | 0.019 | 878.9 | 1.954 | 1.202 |
| 0.80 | 1.730 | 1.485 | 45.271 | 0.018 | 876.9 | 1.924 | 1.184 |
| 0.85 | 1.755 | 1.475 | 44.663 | 0.018 | 875.0 | 1.895 | 1.166 |
| 0.90 | 1.780 | 1.467 | 44.108 | 0.018 | 873.1 | 1.866 | 1.148 |
| 0.95 | 1.805 | 1.461 | 43.601 | 0.017 | 871.3 | 1.839 | 1.131 |
| 1.0 | 1.830 | 1.455 | 43.137 | 0.017 | 869.6 | 1.812 | 1.115 |
Table 5.
N2-O2 property values at 20°C and 1 atm.
| N2 Mole Fraction | ρ (kg/m3) | μ × 105 (kg/s-m) | λ (nm) | k (W/m-K) | cp (J/kg-K) | × 105 (m2/s) | × 105 (m2/s) |
|---|---|---|---|---|---|---|---|
| 0 | 1.330 | 2.029 | 70.561 | 0.026 | 917.5 | 2.551 | 1.573 |
| 0.05 | 1.322 | 2.015 | 70.289 | 0.026 | 922.8 | 2.548 | 1.573 |
| 0.10 | 1.314 | 2.001 | 70.016 | 0.026 | 928.2 | 2.546 | 1.573 |
| 0.15 | 1.306 | 1.987 | 69.743 | 0.026 | 933.7 | 2.543 | 1.573 |
| 0.20 | 1.297 | 1.973 | 69.468 | 0.026 | 939.3 | 2.541 | 1.573 |
| 0.25 | 1.289 | 1.959 | 69.192 | 0.026 | 944.9 | 2.538 | 1.573 |
| 0.30 | 1.281 | 1.945 | 68.915 | 0.026 | 950.6 | 2.536 | 1.573 |
| 0.35 | 1.272 | 1.931 | 68.637 | 0.026 | 956.3 | 2.533 | 1.573 |
| 0.40 | 1.264 | 1.916 | 68.358 | 0.026 | 962.2 | 2.531 | 1.574 |
| 0.45 | 1.256 | 1.902 | 68.077 | 0.026 | 968.1 | 2.529 | 1.574 |
| 0.50 | 1.248 | 1.888 | 67.796 | 0.026 | 974.1 | 2.526 | 1.574 |
| 0.55 | 1.239 | 1.874 | 67.513 | 0.026 | 980.2 | 2.524 | 1.574 |
| 0.60 | 1.231 | 1.860 | 67.230 | 0.026 | 986.3 | 2.521 | 1.574 |
| 0.65 | 1.223 | 1.846 | 66.945 | 0.026 | 992.6 | 2.519 | 1.574 |
| 0.70 | 1.215 | 1.832 | 66.659 | 0.026 | 998.9 | 2.516 | 1.574 |
| 0.75 | 1.206 | 1.818 | 66.371 | 0.026 | 1005.3 | 2.514 | 1.574 |
| 0.78 | 1.201 | 1.809 | 66.198 | 0.026 | 1009.2 | 2.513 | 1.574 |
| 0.79 | 1.200 | 1.806 | 66.141 | 0.026 | 1010.5 | 2.512 | 1.574 |
| 0.80 | 1.198 | 1.803 | 66.083 | 0.026 | 1011.8 | 2.512 | 1.574 |
| 0.85 | 1.190 | 1.789 | 65.793 | 0.026 | 1018.4 | 2.509 | 1.574 |
| 0.90 | 1.181 | 1.775 | 65.502 | 0.025 | 1025.1 | 2.507 | 1.574 |
| 0.95 | 1.173 | 1.761 | 65.210 | 0.025 | 1031.9 | 2.504 | 1.574 |
| 1.0 | 1.165 | 1.747 | 64.916 | 0.025 | 1038.7 | 2.502 | 1.574 |
Table 6.
He-O2 property values at 37°C and 1 atm.
| He Mole Fraction | ρ (kg/m3) | μ × 105 (kg/s-m) | λ (nm) | k (W/m-K) | cp (J/kg-K) | × 105 (m2/s) | × 105 (m2/s) |
|---|---|---|---|---|---|---|---|
| 0 | 1.257 | 2.113 | 75.572 | 0.027 | 920.7 | 2.815 | 1.736 |
| 0.05 | 1.202 | 2.125 | 77.716 | 0.030 | 948.7 | 2.915 | 1.801 |
| 0.10 | 1.147 | 2.137 | 80.012 | 0.034 | 979.3 | 3.023 | 1.871 |
| 0.15 | 1.092 | 2.149 | 82.477 | 0.037 | 1013.0 | 3.139 | 1.947 |
| 0.20 | 1.037 | 2.162 | 85.131 | 0.041 | 1050.3 | 3.264 | 2.029 |
| 0.25 | 0.982 | 2.175 | 87.996 | 0.045 | 1091.7 | 3.400 | 2.118 |
| 0.30 | 0.927 | 2.188 | 91.101 | 0.049 | 1138.1 | 3.547 | 2.215 |
| 0.35 | 0.872 | 2.200 | 94.475 | 0.053 | 1190.3 | 3.708 | 2.322 |
| 0.40 | 0.817 | 2.213 | 98.157 | 0.058 | 1249.5 | 3.883 | 2.440 |
| 0.45 | 0.762 | 2.225 | 102.191 | 0.063 | 1317.3 | 4.077 | 2.570 |
| 0.50 | 0.707 | 2.236 | 106.633 | 0.069 | 1395.7 | 4.291 | 2.714 |
| 0.55 | 0.652 | 2.246 | 111.548 | 0.075 | 1487.2 | 4.528 | 2.876 |
| 0.60 | 0.597 | 2.255 | 117.019 | 0.081 | 1595.6 | 4.793 | 3.059 |
| 0.65 | 0.542 | 2.261 | 123.153 | 0.088 | 1726.0 | 5.091 | 3.266 |
| 0.70 | 0.487 | 2.264 | 130.085 | 0.096 | 1885.8 | 5.429 | 3.504 |
| 0.75 | 0.432 | 2.262 | 137.997 | 0.104 | 2086.3 | 5.814 | 3.779 |
| 0.78 | 0.399 | 2.258 | 143.316 | 0.110 | 2233.2 | 6.073 | 3.965 |
| 0.79 | 0.388 | 2.256 | 145.199 | 0.112 | 2287.7 | 6.165 | 4.032 |
| 0.80 | 0.377 | 2.254 | 147.142 | 0.114 | 2345.3 | 6.259 | 4.100 |
| 0.85 | 0.322 | 2.235 | 157.891 | 0.124 | 2692.7 | 6.777 | 4.481 |
| 0.90 | 0.267 | 2.202 | 170.832 | 0.135 | 3183.0 | 7.389 | 4.941 |
| 0.95 | 0.212 | 2.149 | 187.014 | 0.147 | 3927.4 | 8.122 | 5.505 |
| 1.0 | 0.157 | 2.064 | 208.666 | 0.161 | 5192.4 | 9.016 | 6.216 |
Table 7.
Xe-O2 property values at 37°C and 1 atm.
| Xe Mole Fraction | ρ (kg/m3) | μ × 105 (kg/s-m) | λ (nm) | k (W/m-K) | cp (J/kg-K) | × 105 (m2/s) | × 105 (m2/s) |
|---|---|---|---|---|---|---|---|
| 0 | 1.257 | 2.113 | 75.572 | 0.027 | 920.7 | 2.815 | 1.736 |
| 0.05 | 1.453 | 2.173 | 72.306 | 0.025 | 785.3 | 2.745 | 1.680 |
| 0.10 | 1.648 | 2.221 | 69.409 | 0.024 | 682.0 | 2.678 | 1.627 |
| 0.15 | 1.843 | 2.261 | 66.798 | 0.022 | 600.5 | 2.615 | 1.577 |
| 0.20 | 2.038 | 2.293 | 64.418 | 0.021 | 534.7 | 2.554 | 1.530 |
| 0.25 | 2.233 | 2.319 | 62.231 | 0.020 | 480.3 | 2.496 | 1.486 |
| 0.30 | 2.428 | 2.339 | 60.210 | 0.018 | 434.7 | 2.441 | 1.445 |
| 0.35 | 2.623 | 2.356 | 58.334 | 0.017 | 395.9 | 2.388 | 1.405 |
| 0.40 | 2.818 | 2.369 | 56.586 | 0.016 | 362.4 | 2.337 | 1.368 |
| 0.45 | 3.013 | 2.378 | 54.951 | 0.015 | 333.3 | 2.289 | 1.333 |
| 0.50 | 3.208 | 2.386 | 53.419 | 0.014 | 307.7 | 2.242 | 1.299 |
| 0.55 | 3.404 | 2.391 | 51.980 | 0.013 | 285.1 | 2.197 | 1.267 |
| 0.60 | 3.599 | 2.395 | 50.625 | 0.012 | 264.9 | 2.154 | 1.237 |
| 0.65 | 3.794 | 2.397 | 49.346 | 0.011 | 246.7 | 2.113 | 1.208 |
| 0.70 | 3.989 | 2.397 | 48.138 | 0.010 | 230.4 | 2.073 | 1.180 |
| 0.75 | 4.184 | 2.397 | 46.995 | 0.009 | 215.6 | 2.035 | 1.154 |
| 0.80 | 4.379 | 2.396 | 45.911 | 0.008 | 202.1 | 1.998 | 1.129 |
| 0.85 | 4.574 | 2.393 | 44.882 | 0.008 | 189.7 | 1.962 | 1.105 |
| 0.90 | 4.769 | 2.391 | 43.904 | 0.007 | 178.4 | 1.928 | 1.081 |
| 0.95 | 4.964 | 2.387 | 42.973 | 0.006 | 168.0 | 1.895 | 1.059 |
| 1.0 | 5.159 | 2.384 | 42.086 | 0.006 | 158.3 | 1.863 | 1.038 |
Table 8.
N2O-O2 property values at 37°C and 1 atm.
| N2O Mole Fraction | ρ (kg/m3) | μ × 105 (kg/s-m) | λ (nm) | k (W/m-K) | cp (J/kg-K) | × 105 (m2/s) | × 105 (m2/s) |
|---|---|---|---|---|---|---|---|
| 0 | 1.257 | 2.113 | 75.572 | 0.027 | 920.7 | 2.815 | 1.736 |
| 0.05 | 1.281 | 2.039 | 72.254 | 0.027 | 918.4 | 2.759 | 1.701 |
| 0.10 | 1.305 | 1.974 | 69.300 | 0.026 | 916.2 | 2.705 | 1.668 |
| 0.15 | 1.328 | 1.916 | 66.666 | 0.025 | 914.0 | 2.653 | 1.635 |
| 0.20 | 1.352 | 1.864 | 64.312 | 0.025 | 911.9 | 2.603 | 1.604 |
| 0.25 | 1.376 | 1.819 | 62.203 | 0.024 | 909.9 | 2.555 | 1.574 |
| 0.30 | 1.399 | 1.779 | 60.311 | 0.024 | 908.0 | 2.509 | 1.546 |
| 0.35 | 1.423 | 1.743 | 58.611 | 0.023 | 906.1 | 2.464 | 1.518 |
| 0.40 | 1.446 | 1.712 | 57.080 | 0.023 | 904.3 | 2.421 | 1.491 |
| 0.45 | 1.470 | 1.684 | 55.700 | 0.022 | 902.5 | 2.379 | 1.465 |
| 0.50 | 1.494 | 1.659 | 54.454 | 0.022 | 900.8 | 2.339 | 1.440 |
| 0.55 | 1.517 | 1.638 | 53.327 | 0.021 | 899.1 | 2.300 | 1.416 |
| 0.60 | 1.541 | 1.619 | 52.307 | 0.021 | 897.5 | 2.262 | 1.393 |
| 0.65 | 1.564 | 1.602 | 51.382 | 0.021 | 896.0 | 2.226 | 1.370 |
| 0.70 | 1.588 | 1.588 | 50.543 | 0.020 | 894.5 | 2.190 | 1.348 |
| 0.75 | 1.612 | 1.576 | 49.780 | 0.020 | 893.0 | 2.156 | 1.327 |
| 0.80 | 1.635 | 1.565 | 49.087 | 0.020 | 891.6 | 2.123 | 1.306 |
| 0.85 | 1.659 | 1.556 | 48.455 | 0.019 | 890.2 | 2.091 | 1.286 |
| 0.90 | 1.683 | 1.549 | 47.880 | 0.019 | 888.9 | 2.060 | 1.267 |
| 0.95 | 1.706 | 1.542 | 47.355 | 0.019 | 887.6 | 2.030 | 1.248 |
| 1.0 | 1.730 | 1.537 | 46.876 | 0.018 | 886.3 | 2.000 | 1.230 |
Table 9.
N2-O2 property values at 37°C and 1 atm.
| N2 Mole Fraction | ρ (kg/m3) | μ × 105 (kg/s-m) | λ (nm) | k (W/m-K) | cp (J/kg-K) | × 105 (m2/s) | × 105 (m2/s) |
|---|---|---|---|---|---|---|---|
| 0 | 1.257 | 2.113 | 75.572 | 0.027 | 920.7 | 2.815 | 1.736 |
| 0.05 | 1.250 | 2.098 | 75.262 | 0.027 | 925.9 | 2.812 | 1.736 |
| 0.10 | 1.242 | 2.083 | 74.950 | 0.027 | 931.2 | 2.810 | 1.736 |
| 0.15 | 1.234 | 2.067 | 74.638 | 0.027 | 936.6 | 2.807 | 1.736 |
| 0.20 | 1.226 | 2.052 | 74.324 | 0.027 | 942.0 | 2.804 | 1.737 |
| 0.25 | 1.218 | 2.037 | 74.010 | 0.027 | 947.5 | 2.802 | 1.737 |
| 0.30 | 1.211 | 2.022 | 73.694 | 0.027 | 953.1 | 2.799 | 1.737 |
| 0.35 | 1.203 | 2.006 | 73.377 | 0.027 | 958.7 | 2.796 | 1.737 |
| 0.40 | 1.195 | 1.991 | 73.059 | 0.027 | 964.4 | 2.793 | 1.737 |
| 0.45 | 1.187 | 1.976 | 72.740 | 0.027 | 970.2 | 2.791 | 1.737 |
| 0.50 | 1.179 | 1.961 | 72.420 | 0.027 | 976.1 | 2.788 | 1.737 |
| 0.55 | 1.171 | 1.946 | 72.098 | 0.027 | 982.0 | 2.785 | 1.737 |
| 0.60 | 1.164 | 1.931 | 71.776 | 0.027 | 988.0 | 2.783 | 1.737 |
| 0.65 | 1.156 | 1.915 | 71.452 | 0.027 | 994.1 | 2.780 | 1.737 |
| 0.70 | 1.148 | 1.900 | 71.127 | 0.027 | 1000.3 | 2.777 | 1.737 |
| 0.75 | 1.140 | 1.885 | 70.801 | 0.027 | 1006.6 | 2.775 | 1.737 |
| 0.78 | 1.135 | 1.876 | 70.605 | 0.027 | 1010.4 | 2.773 | 1.737 |
| 0.79 | 1.134 | 1.873 | 70.539 | 0.027 | 1011.6 | 2.773 | 1.737 |
| 0.80 | 1.132 | 1.870 | 70.474 | 0.027 | 1012.9 | 2.772 | 1.737 |
| 0.85 | 1.124 | 1.855 | 70.145 | 0.026 | 1019.4 | 2.769 | 1.737 |
| 0.90 | 1.117 | 1.840 | 69.815 | 0.026 | 1025.9 | 2.767 | 1.737 |
| 0.95 | 1.109 | 1.824 | 69.484 | 0.026 | 1032.5 | 2.764 | 1.737 |
| 1.0 | 1.101 | 1.809 | 69.152 | 0.026 | 1039.2 | 2.761 | 1.737 |
Table 10.
Binary diffusivities at 1 atm.
| Gas | × 105 (m2/s) | |
|---|---|---|
| 20°C | 37°C | |
| He-O2 | 7.142 | 7.883 |
| Xe-O2 | 1.243 | 1.372 |
| N2O-O2 | 1.415 | 1.561 |
| N2-O2 | 1.999 | 2.206 |
Figure 1.
Density of gas mixtures at 20°C and 1 atm.
Figure 2.
Viscosity of gas mixtures at 20°C and 1 atm.
Figure 3.
Mean free path of gas mixtures at 20°C and 1 atm.
Figure 4.
Thermal conductivity of gas mixtures at 20°C and 1 atm.
Figure 5.
Specific heat of gas mixtures at 20°C and 1 atm.
Discussion
In this paper thermophysical property values have been presented for inhaled therapeutic binary gas mixtures. Pure substance values at 20°C and 37°C and mixing formulas based on kinetic theory were used to estimate the mixture values. The approach was to use relatively simple estimates for nonpolar gases [8]. That is, more complex intermolecular interactions that occur, for example, at high pressure, were not included.
Whereas many therapeutic gases (e.g.; CO and NO) are used at trace concentrations such that property values of the bulk mixture are essentially equivalent to those of air, mixtures considered herein have significantly different properties than air which change as a function of component concentration. Mechanical property values of density and viscosity are fundamental to the understanding of gas transport and airway resistance. The thermal properties of conductivity and capacity are necessary to accurately predict how gas treatments will affect the temperature and humidity of the respiratory tract. They also will influence the thermodynamic interaction of inhaled aerosols with the gas, and thus the deposition distribution which is particularly relevant for helium-oxygen mixtures. Diffusion is a key mode of gas transport deep in the lung potentially affecting exchange with the blood.
Bird et al. [8] note that the concept of the mean free path is applicable only if there are no long range forces associated with the hard sphere kinetic theory models. For this reason it is not typically an element of modern kinetic theory. Nevertheless, it is an important parameter in modeling the interaction of aerosols and gases [19], and thus for combination therapies involving aerosols and gas mixtures. In contrast to the scheme employed by Loeb [20], the estimation method employed here does not directly take into account the molecular collisions. However, Equation (6) for the mean free path does account for the collisions of different molecules through the mixture viscosity. As the utility of this parameter in aerosol mechanics is to estimate a reduced drag on small particles where their size is comparable to the mean free path, this approach would appear to be self consistent.
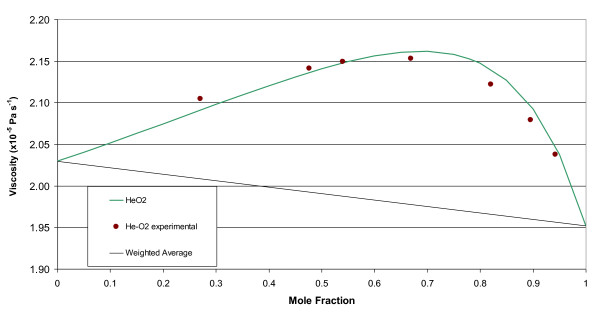
A comparison of estimated data based on Equation (3) to experimental data for the viscosity at 20°C of helium-oxygen mixtures [14] is shown in Figure 6, along with the linear curve representing the concentration weighted average. The maximum relative difference of 0.9% between the theory and experiment occurs at XHe = 0.82. For the concentration weighted average value the maximum relative error of 7.9% occurs at XHe = 0.67.
Figure 6.
Viscosity of He-O2 mixtures using Equation (3), based on a weighted average of the molar fractions and from experimental measurements [14].
Figure 7 shows comparisons of experimental thermal conductivity values [17] for helium-oxygen and xenon-oxygen mixtures at 30°C compared to theoretical values calculated using Equation (8). The maximum relative differences between the theory and experiment are 4.2% at XHe = 0.68 and 4.7% at XXe = 0.27, respectively.
Figure 7.
Thermal conductivity at 30°C for He-O2 and Xe-O2 mixtures using Equation (8), based on a weighted average of the molar fractions and from experimental measurements [17].
Table 11 shows a good agreement between experimental data for binary diffusivity of He-O2 and Xe-O2 [14,21] with theoretical data calculated using Equation (10). For the diffusivity of water vapor or carbon dioxide, the simplifying assumption leading to Blanc's law is for a trace component diffusing into a homogeneous, binary mixture. A quantitative definition of trace for the applicability of this assumption was not found. However, experiments testing diffusion of He, CO and SF6 through gas mixtures similar to alveolar gas (14% O2, 6% CO2 and 80% N2) did not show significant departures from values predicted on the basis of binary diffusion coefficient values weighted according to fractional concentrations [22] in agreement with Blanc's law. These experiments were performed with test gas concentrations varying from 0 to 10% suggesting Blanc's law would be appropriate for typical applications of the gases considered herein.
Table 11.
Comparison of experimental and theoretical binary diffusivities based on Equation (10).
In conclusion, the methods presented above allow accurate estimation of thermophysical property values for inhaled therapeutic binary gas mixtures, including He-O2, Xe-O2, and N2O-O2, over a range of concentrations.
Competing interests
The authors declare that they have no competing interests.
Authors' contributions
All of the authors have read and approved the final manuscript.
IK determined the appropriate models, wrote the software to implement the models and drafted the manuscript.
GC provided assistance with determining the models, implementing the software and edited the manuscript.
AM provided assistance with determining the models, implementing the software and edited the manuscript.
PA provided experimental data from the literature and edited the manuscript.
Contributor Information
Ira Katz, Email: ira.katz@airliquide.com.
Georges Caillibotte, Email: georges.cailbotte@airliquide.com.
Andrew R Martin, Email: andrew-r.martin@airliquide.com.
Philippe Arpentinier, Email: philippe.arpentinier@airliquide.com.
Acknowledgements
We thank Paul Finlay for performing some of the calculations.
References
- Anderson M, Svartengren M, Bylin G, Philipson K, Camner P. Deposition in asthmatics of particles inhaled in air or helium-oxygen. Am Rev Respir Dis. 1993;147:524–528. doi: 10.1164/ajrccm/147.3.524. [DOI] [PubMed] [Google Scholar]
- Baumert J-H, Reyle-Hahn M, Hecker K, Tenbrinck R, Kuhien R, Rossaint R. Increased airway resistance during xenon anaesthesia in pigs is attributed to physical properties of the gas. Brit Anaesthesia. 2002;88:540–545. doi: 10.1093/bja/88.4.540. [DOI] [PubMed] [Google Scholar]
- Darquenne C, Prisk GK. Aerosol deposition in the human respiratory tract breathing air and 80:20 heliox. J Aerosol Med. 2004;17:278–285. doi: 10.1089/jam.2004.17.278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frazier MD, Cheifetz IM. The role of heliox in paediatric respiratory disease. Paediatric Respiratory Reviews. 2010;11:46–53. doi: 10.1016/j.prrv.2009.10.008. [DOI] [PubMed] [Google Scholar]
- Hess DR, Fink JB, Venkataraman ST, Kim IK, Meyers TR, Tano BD. The history and physics of heliox. Respir Care. 2006;51:608–612. [PubMed] [Google Scholar]
- Mihaescu M, Gutmark E, Murugappan S, Elluru R, Cohen A, Willging P. Modeling flow in a compromised pediatric airway breathing air and heliox. Laryngoscope. 2009;119:145–151. doi: 10.1002/lary.20015. [DOI] [PubMed] [Google Scholar]
- Palange P, Valli G, Onorati P, Antonucci R, Paoletti P, Rosato A, Manfredi F, Serra P. Effect of heliox on lung dynamic hyperinflation, dyspnea, and exercise endurance capacity in COPD patients. J Appl Physiol. 2004;97:1637–1642. doi: 10.1152/japplphysiol.01207.2003. [DOI] [PubMed] [Google Scholar]
- Bird GA, Stewart WE, Lightfoot EN. Transport Phenomena. New York: John Wiley & Sons; 1960. [Google Scholar]
- Poling BE, Prausnitz JM, O'Connel JP. The Properties of Gases and Liquids. 5. New York: McGraw-Hill; 2007. [Google Scholar]
- Reid RC, Sherwood TK. The Properties of Gases and Liquides: Their Estimation and Correlation. 2. New York: McGraw-Hill; 1966. [Google Scholar]
- Bzowski J, Kestin J, Mason EA, Uribe FJ. Equilibrium and transport properties of gas mixtures at low density: Eleven polyatomic gases and five noble gases. J Phys Chem Ref Data. 1990;19:1179–1232. doi: 10.1063/1.555867. [DOI] [Google Scholar]
- Hellemans JM, Kestin J, Ro ST. The viscosity of oxygen and of some of its mixtures with other gases. Physica. 1973;65(2):362–375. doi: 10.1016/0031-8914(73)90351-0. [DOI] [Google Scholar]
- Hellemans JM, Kestin J, Ro ST. On the properties of multicomponent mixtures of monatomic gases. Physica. 1974;71(1):1–16. doi: 10.1016/0031-8914(74)90043-3. [DOI] [Google Scholar]
- Kestin J, Khalifa HE, Ro ST, Wakeham WA. The viscosity and diffusion coefficients of eighteen binary gas systems. Physica. 1977;88A:242–260. [Google Scholar]
- Kestin J, Khalifa HE, Wakeham WA. The viscosity and diffusion coefficients of the binary mixtures of xenon with the other noble gases. Physica A: Statistical and Theoretical Physics. 1978;90(2):215–228. doi: 10.1016/0378-4371(78)90110-3. [DOI] [Google Scholar]
- Kestin J, Knierim K, Mason EA, Najafi B, Ro ST, Waldman M. Equilibrium and transport properties of the noble gases and their mixtures at low density. J Phys Chem Ref Data. 1984;13:229–303. doi: 10.1063/1.555703. [DOI] [Google Scholar]
- Srivastava BN, Barua AK. The dilute gas thermal conductivity of the binary mixtures O2 - He, O2 - Ne, O2 - Kr and O2 - Xe is measured at 30 C and 45 C for various compositions by using the thick-wire variant of the hot-wire method. J Chem Phys. 1960;32:427–435. doi: 10.1063/1.1730711. [DOI] [Google Scholar]
- Bird GA. Definition of mean free path for real gases. Phys Fluids. 1983;26:3222–3223. doi: 10.1063/1.864095. [DOI] [Google Scholar]
- Issacs KK, Rosati JA, Martonen TB. In: Aerosols Handbook: Measurement, Dosimetry, and Health Effects. Ruzer LS, Harley NH, editor. CRC Press LLC; 2005. Mechanisms of particle deposition; pp. 73–97. [Google Scholar]
- Loeb LB. The Kinetic Theory of Gases. 3. New York: Dover Publications, Inc; 1961. [Google Scholar]
- Dunlop PJ, Bignelli CM. The temperature and concentration dependences of diffusion coefficients of the systems Ne-O2, K-O2, Xe-O2 and He-NO. Ber Bunsen-Ges. 1992;96:1847–1848. [Google Scholar]
- Worth H, Piper J. Diffusion of helium, carbon monoxide and sulfur hexafluoride in gas mixtures similar to alveolar gas. Respir Physiol. 1978;32:155–166. doi: 10.1016/0034-5687(78)90106-8. [DOI] [PubMed] [Google Scholar]