Algorithm 1.
Outline of our approach, showing the use of cross-validation to estimate training set error and the use of multiple prediction models. The running time depends on the supervised feature prediction algorithm(s) and is otherwise linear in the number of features and feature predictors.
input:N training examples
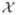 = {x1,x2, …,xN }, any number of test examples xq = {x1,x2, …,xN }, any number of test examples xq
|
| for each feature i ∈ {1, 2, …, D} do |
| for each feature prediction model p ∈ {1, 2, …, P} do |
| Ap,i ← ∅//Ap,i will be a set of training set |
| //(observed feature value, predicted feature value) pairs we can use to |
| //build an error model to estimate P(xqi |Cp,i (ρi (xq))) for anyxq |
| for each cross-validation fold fdo |
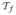 , ,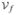 ← divide( ← divide(
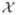 , f)//divide , f)//divide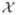 into a training set into a training set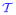
|
//and a validation set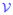 , unique to this fold , unique to this fold
|
valsetf ← (ρi (x), xji) for each xj ∈
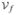
|
trainset f ← (ρi (x), xji) for each xj ∈
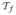
|
| Cp,i, f ← train p(trainset f)//learn a feature i predictor using model p |
| Ap,i ← Ap,i ∪ (xji, Cp,i, f (ρi (xj))) for each xj ∈ valset f |
| end for |
| Ep,i ← error_model(A p,i)//model the distribution of error A p,i |
| //(the model type depends on the type of feature i, see text) |
trainset ← (ρi (xj), xji) for each xj ∈
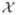
|
| Cp,i ← train(trainset)//the “final” predictor trained on the entire |
//training set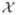 , used to make test set predictions , used to make test set predictions
|
| end for |
| end for |
| for each test example xqdo |
| //output the normalized surprisal score as the sum |
| //over P feature prediction models. |
| //P(xqi) depends on C p,i (ρi (xq))) and E p,i. |
| output: |
| end for |
