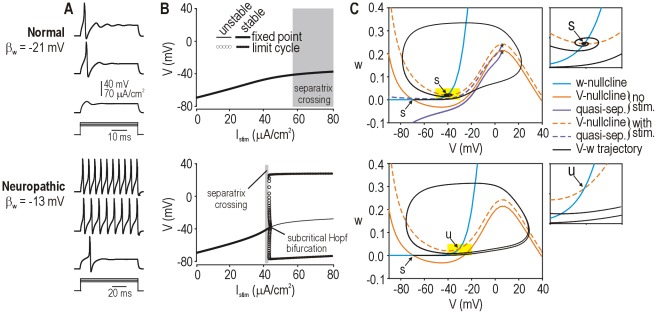
Figure 2. Simulation and dynamical explanation of change in spiking pattern.

(A) Spiking pattern during sustained depolarization was converted from onset-only (normal, β_w = −21 mV) to repetitive (neuropathic, β_w = −13 mV) by varying a single parameter. Onset-only spiking was observed in the neuropathic model but for only a narrow stimulus range. (B) According to bifurcation analysis in which stimulation (I _stim) was systematically varied, repetitive spiking was produced by the neuropathic model when I _stim exceeded a critical value required for a subcritical Hopf bifurcation. In contrast, the normal model did not undergo a bifurcation, which means spiking was limited to single spikes generated through a QS-crossing (see below). Generation of a single spike does not constitute a change in steady-state behavior, consistent with the absence of a bifurcation. (C) Phase planes show the fast activation variable V plotted against the slower recovery variable w. Nullclines (color) indicate where V or w do not change. Excitatory stimulation shifts the V-nullcline upward without affecting the w-nullcline. In the neuropathic model, V- and w-nullclines intersect at a stable (s) fixed point prior to stimulation, but that point becomes unstable (u) during stimulation – this corresponds to a Hopf bifurcation and is responsible for repetitive spiking. In the normal model, the fixed point remains stable during stimulation despite the V-nullcline shifting upward, but a single spike can nonetheless be generated depending on how the system moves to the newly positioned fixed point. The trajectory can be predicted by reference to a quasi-separatrix (QS), which corresponds to a manifold in phase space from which trajectories diverge. Quasi-separatrices were plotted here by integrating with a negative time step with initial values indicated by * on the phase planes (see Methods). Like the V-nullcline, the QS shifts instantaneously with stimulation. If, as shown, the original fixed point ends up below the shifted QS, the trajectory to the newly positioned fixed point must follow an indirect route around the end of the QS (*), thus producing a spike; a more direct, subthreshold route would require the trajectory to cross back over the QS, which is not possible. If the original fixed point remained above the shifted QS, the trajectory would follow a direct route and no spike would be produced (not illustrated).