Generic temperature compensation of biological clocks by autonomous regulation of catalyst concentration

Abstract

Circadian clocks—ubiquitous in life forms ranging from bacteria to multicellular organisms—often exhibit intrinsic temperature compensation; the period of circadian oscillators is maintained constant over a range of physiological temperatures, despite the expected Arrhenius form for the reaction coefficient. Observations have shown that the amplitude of the oscillation depends on the temperature but the period does not; this suggests that although not every reaction step is temperature independent, the total system comprising several reactions still exhibits compensation. Here we present a general mechanism for such temperature compensation. Consider a system with multiple activation energy barriers for reactions, with a common enzyme shared across several reaction steps. The steps with the highest activation energy rate-limit the cycle when the temperature is not high. If the total abundance of the enzyme is limited, the amount of free enzyme available to catalyze a specific reaction decreases as more substrates bind to the common enzyme. We show that this change in free enzyme abundance compensates for the Arrhenius-type temperature dependence of the reaction coefficient. Taking the example of circadian clocks with cyanobacterial proteins KaiABC, consisting of several phosphorylation sites, we show that this temperature compensation mechanism is indeed valid. Specifically, if the activation energy for phosphorylation is larger than that for dephosphorylation, competition for KaiA shared among the phosphorylation reactions leads to temperature compensation. Moreover, taking a simpler model, we demonstrate the generality of the proposed compensation mechanism, suggesting relevance not only to circadian clocks but to other (bio)chemical oscillators as well.

The circadian clock is one of the most remarkable cyclic behaviors ubiquitous to the known forms of life, ranging from the unicellular to the multicellular level—including prokaryotes. Because of its importance, the underlying chemical reactions have been the subject of academic interest for a long time and have recently been elucidated experimentally. Thus, we now know that circadian clocks have three important features:

1. They persist in the absence of external cues with an approximately 24-h period, which is rather long compared with most chemical reactions.

2. They can be reset by exposure to external stimuli such as changes in illumination (dark/light) or temperature.

3. The period of the circadian clock is robustly maintained across a range of physiological temperatures. (temperature compensation) (1, 2).

Generally, the rate of chemical reactions depends strongly on the temperature. Indeed, most biochemical reactions have an energy barrier that must be overcome with the aid of enzymes, and thus the rate can be expected to follow the Arrhenius form. For this reason, the period of chemical or biochemical oscillators can be expected to strongly depend on the temperature (3). However, this is not case: Temperature-compensated biological circadian clocks are ubiquitous, which suggests some common mechanism(s) behind them. Although the emergence of cyclic behavior with a capacity for entrainment is theoretically understood as being a result of the existence of a limit-cycle attractor in a class of dynamical systems described by chemical rate equations, this does not provide a mechanism that can explain temperature compensation.

Overall, there are two possibilities for such a mechanism: One is that compensation exists at each elementary step, and the other is that compensation occurs at the system level, for the total set of enzymatic reactions. Recently, it was found that the rates of some elementary reaction steps in circadian clocks depend only slightly on temperature (4, 5), suggesting that the activation energy barrier of some reactions is rather low. This suggests element-level compensation. However, it is difficult to imagine that every reaction step is fully temperature-compensated at the single-molecule level. Indeed, if that were the case, temperature changes would not influence the oscillation of chemical concentrations at all. In contrast, it is known that the amplitude changes indeed depend on temperature (6–8), even though the period does not. Furthermore, circadian clocks are known to entrain to external temperature cycles, and they can be reset by temperature cues (6, 9, 10). Although temperature changes can influence the oscillation, the period is still robust.

Hence, it is necessary to search for a general logic that underlies the temperature compensation phenomenon at the system level. Indeed, several models have been proposed (11–16). In most of the system-level studies, several processes that are responsible for the period are considered that cancel out each other’s temperature dependence. This is a balance mechanism by which temperature compensation can be achieved. Such a mechanism, however, requires a fine-tuned set of parameters or, rather, an ad hoc combination of processes for balancing. Considering the ubiquity of temperature compensation, a generic and robust mechanism that does not require tuning parameters is desirable. Here we propose such a mechanism that has general validity for any biochemical oscillator consisting of several reaction processes catalyzed by enzymes. The mechanism can be briefly outlined as follows:

Biochemical clocks comprise multiple processes, such as phosphorylation and dephosphorylation, with each generally having a different activation energy barrier ΔE. The rate of such reactions, then, is given by kA_f exp(-ΔE/T), where A_f is the concentration of “free” enzyme available, and k is the rate constant for it. If the enzyme concentration were insensitive to temperature, the rate would just agree with the simple Arrhenius form, thus implying high temperature dependence. Now, consider a situation where several substrates share the same enzyme. At lower temperature, the reactions with higher activation energy will be slower and the substrates involved in these reactions will accumulate. Then, because they share the same enzyme, competition for the enzyme will also increase. Accordingly, the concentration of available (free) enzyme decreases, and when it reaches a level satisfying 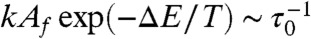, where τ₀ is the inherent time scale of the system ( 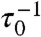is the basic reaction rate), these enzymatic reactions will be highly suppressed. The system spends most of its time under such conditions, which limits the rate. Thus, the Arrhenius-type temperature dependence is compensated for by the concentration of available enzyme as A_f exp(-ΔE/T) ∼ (τ₀k)^-1.

Although this is a rather basic description, its validity may suggest that temperature compensation emerges in any general chemical oscillation consisting of steps, catalyzed by a common enzyme. Here, we first study the validity of this enzyme-limited temperature compensation mechanism for the specific case of the Kai protein clock model introduced by van Zon et al. (17) to explain the circadian clock of KaiABC proteins in cyanobacteria, which was discovered by Kondo and his colleagues (8, 18). Indeed, in this system, the period of circadian oscillation of Kai proteins is temperature-compensated (8). Further, although some of the elementary components in this system, specifically, KaiC’s ATPase activity and KaiC’s phosphatase activity, were suggested to depend only slightly on temperature (4, 19), the origin of system-level temperature compensation has not yet been explained without imposing a balance mechanism. Here, we show numerically that system-level temperature compensation emerges due to competition for limited enzymes, without the need for tuning parameter values. Furthermore, we elucidate the conditions necessary for this temperature compensation to work. Then, based on this analysis, we illustrate the above mechanism with a simpler model consisting of a few catalytic reactions. Possible relations between our results and reported experimental findings for circadian clocks are also discussed.

Model

The Kai-protein-based circadian clock, discovered by Kondo’s group, consists of KaiA, KaiB, KaiC proteins with ATP as an energy source (8). KaiC has a hexameric structure with six monomers, each with two phosphorylation sites (20). It has both autokinase activity and autophosphatase activity, but the autophosphatase activity is usually stronger, and so it is spontaneously dephosphorylated (21, 22). KaiA, in a dimer form (20), attaches to KaiC and thus increases its kinase activity, leading to phosphorylation of KaiC (22, 23), whereas KaiB inhibits the activity of KaiA (22, 24). This phosphorylation/dephosphorylation process of the KaiABC proteins constitutes a circadian rhythm. Here, we simplify the process, to focus on the temperature compensation of the period. We reduce the two phosphorylation residues to just one, because abundance of singly phosphorylated KaiC is strongly correlated with that of doubly phosphorylated KaiC (25) so that the phosphorylation of the two residues are equilibrated on a rather short time scale. Next, we do not include KaiB explicitly in our model, because changes in the concentration of KaiB affect the period only slightly (26). Note that although KaiB is necessary to generate circadian oscillations, the effect can be accounted for by introducing a parameter value for KaiA activity. Here, we adopt a slightly simplified version of the model introduced by van Zon et al. (17) (see also refs. 27–31).

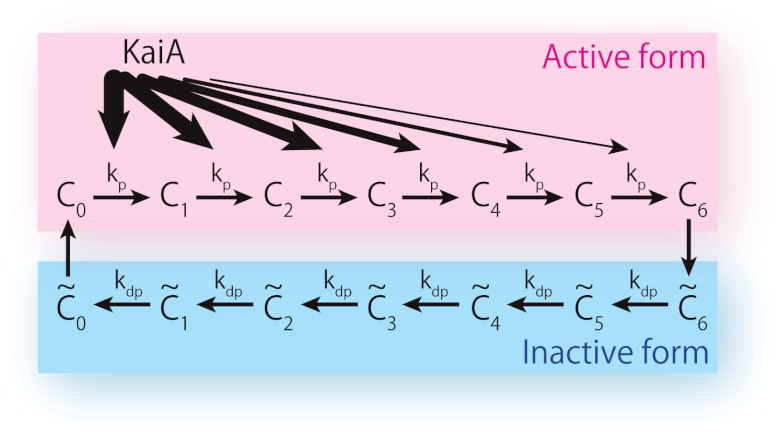
First, each KaiC monomer has two states—active and inactive. Second, allosterically regulated KaiC hexamers in the active state can be phosphorylated, whereas those in the inactive state can be dephosphorylated. A phosphorylated KaiC monomer energetically prefers the inactive state, whereas a dephosphorylated KaiC has the opposite tendency. Here the flip-flop transition between active and inactive states occurs only from the fully phosphorylated or fully dephosphorylated states, as assumed in the concerted MWC model (32). No intermediate states are assumed. Hence, the reaction process exhibits a cyclic structure as in Fig. 1.

Fig. 1.

Simplified model of circadian clock involving KaiAC proteins based on van Zon et al. (17). A KaiC hexamer, with six phosphorylation sites, can also take an active or inactive state. In the active state, KaiC phosphorylation is catalyzed by KaiA at the rate k_p, whereas in the inactive state, dephosphorylation progresses without any enzymes at the rate k_dp. Affinity between active KaiC and KaiA reduces as the number of phosphorylated sites of KaiC increases.

Next, KaiA facilitates phosphorylation of active KaiC with an affinity that depends on the number of phosphorylated residues of each KaiC hexamer. KaiCs with a smaller phosphorylation number have stronger affinity to KaiA. This assumption is necessary for generating stable oscillations (17). Then, the reactions are given by

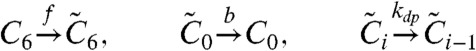[1]

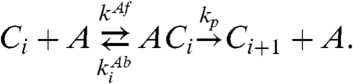[2]

Here C_i and 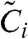denote the concentrations of active KaiC and inactive KaiC, respectively, with i phosphorylated sites; A denotes the concentration of free KaiA dimer. To study the temperature compensation of the period, we must also account for the temperature dependence of the reaction rate. Here, the rates of phosphorylation and dephosphorylation are governed by the Arrhenius equation. Then the rate constants k_dp and k_p are as follows:

[3]

with inverse temperature β(β = 1/T) by taking the unit of Boltzmann constant as unity. We could include the temperature dependence of the rates f and b in a similar manner, but as the reaction between active and inactive states progresses faster and does not influence the period (17), this dependence is neglected. Even if f and b are temperature-dependent, the conclusion below does not change, because the corresponding process in (1) is faster than others. Here, the formation and dissociation of KaiAC complexes occur at much faster rates than other reactions and so are eliminated adiabatically. Thus, the change in the concentration A is given by

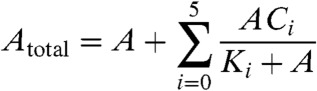[4]

where 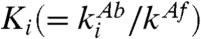are the dissociation constants. Considering the decrease in affinity for KaiA with the number of phosphorylated sites, we set K_i = K₀αⁱ(α > 1.0). We adopted the deterministic rate equation given by the mass-action kinetics, and it is simulated by using the fourth-order Runge-Kutta method.

van Zon et al. demonstrated that temperature compensation occurs when the speed of phosphorylation and dephosphorylation is completely temperature-compensated at the level of elementary reaction process. However, it cannot explain why the amplitude of oscillation depends on temperature or why entrainment to temperature cycles occurs. A compensation mechanism that works at the system level is necessary.

Results

Oscillation at Varied Temperature.

As mentioned, a KaiC allosteric model was analyzed. Specifically, we studied the case in which the activation energy for phosphorylation, E_p, is larger than that of dephosphorylation, E_dp. See the supporting information for other cases.

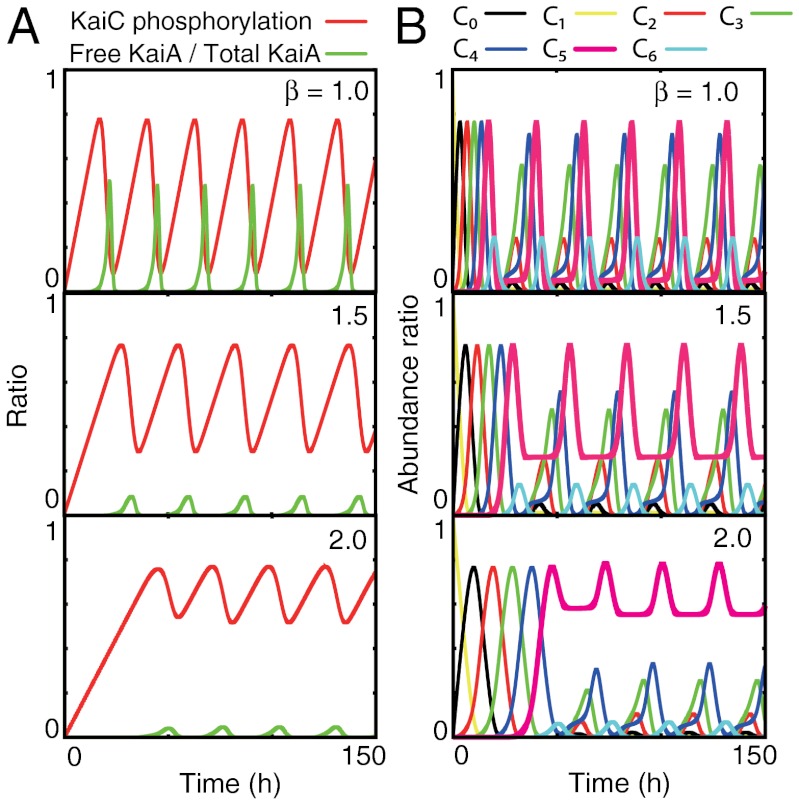
For a certain range of parameter values, we found periodic oscillation in the KaiC phosphorylation level and free KaiA abundance, as shown in the time series in Fig. 2A. The oscillation is described by a limit-cycle attractor, as represented in the orbit in a two-dimensional plane representing KaiC phosphorylation level and free KaiA abundance (SI Appendix, Fig. S1). As the temperature increases, the amplitude of the limit-cycle increases (Fig. 2A). Lowering the temperature causes a decrease in the maximum amount of free KaiA and an increase in the minimum level of KaiC phosphorylation. Further lowering it, however, results in the limit-cycle changing into a stable fixed point via Hopf bifurcation. The time series of C_i(i = 0,1,2, ..,6) and the temperature dependence are shown in Fig. 2B. With a decrease in temperature, we see an increase in C₅—that is, the abundance of KaiC with five phosphorylated residues (5P-KaiC), which leads to an increase in the minimum KaiC phosophorylation level, as shown in Fig. 2B.

Fig. 2.

Oscillations in KaiC phosphorylation at various temperatures (β = 1.0,1.5,2.0). (A) Red line indicates the time series of the mean phosphorylation level defined by 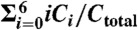, whereas the green line indicates that of the fraction of free KaiA, A/A_total. A decrease in temperature causes a decrease in the amplitude of the phosphorylation level. (B) Time course of the abundance of each form of KaiC, C_i. At low temperature, the basal amount of C₅ (magenta line) is remarkably high.

Transition to Temperature Compensation.

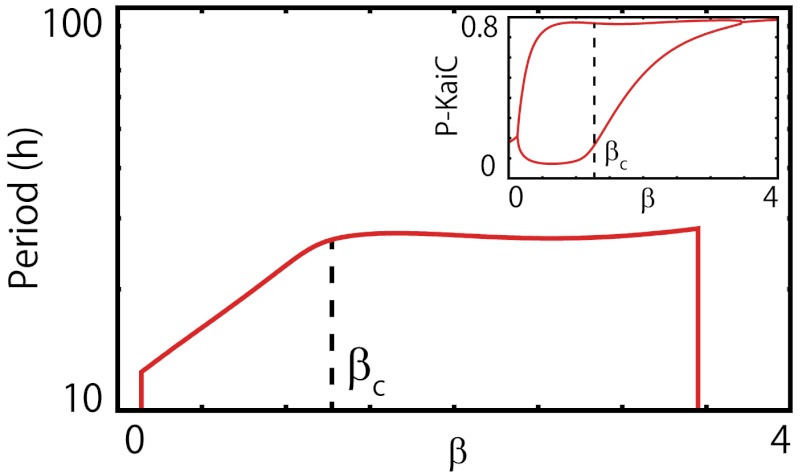
The transition at β ≃ β_c = 1/T_c ≈ 1.2 is also reflected in the temperature dependence of the period. We plotted the period of oscillation as a function of (inverse) temperature, together with the maximum and minimum KaiC phosphorylation levels (see Fig. 3). Above T_c, the temperature dependence of the period follows exp(βE_p), as can be naturally expected from a reaction process with a jump beyond the energy barrier. However, at lower temperature, the period is no longer prolonged exponentially and is nearly constant. Thus, the temperature compensation of the circadian period appears at lower temperature. There is also a clear difference in the amplitude of oscillation below and above T_c. At higher temperature (without temperature compensation), the amplitude of oscillation is almost constant over a large interval of temperatures. However, at lower temperature (with temperature compensation), the amplitude decreases with lower temperature; eventually, the oscillation disappears via Hopf bifurcation. This decrease in amplitude is due to the increase in the minimum value of the KaiC phosphorylation level, caused by the increase in the minimum abundances of C₅. The temperature dependences of the abundance of each KaiC and free KaiA also show distinct behaviors below and above T_c (see Fig. 4 and SI Appendix, Fig. S3). The average and minimum abundances of C₅ increase remarkably with a decrease in temperature below T_c, whereas the maximum hardly changes with temperature (Fig. 4A). Because the reaction from C₅ to C₆ becomes a bottleneck at lower temperature, the accumulation of C₅ occurs. However, the amplitude of the oscillation of C_i(0 ≤ i ≤ 4) has a peak at around T_c, and the minimum value increases as the temperature decreases. The minimum value of free KaiA increase when the temperature is decreased. The minimum inactive KaiC abundance (independent of the number of phosphorylated subunits on the KaiC hexamer) and C₆ showed behaviors similar to those of C_i(0 ≤ i ≤ 4), whereas the average followed exp(-β(E_p - E_dp)) dependence throughout the temperature range. Considering that the total amount of all KaiCs is conserved and the difference in activation energy, this dependence itself is rather natural.

Fig. 3.

Dependence of period of oscillation on the inverse temperature β = 1/T. At high temperature (low β), the period changes exponentially with β, whereas above β_c = 1/T_c ≈ 1.2—i.e., at temperatures below the critical temperature T_c—the period is nearly constant against changes in temperature. (Inset: Maximum and minimum values of mean phosphorylation level over a cycle. The maximum value is nearly constant against temperature changes, whereas the minimum value increases with β above β_c. The oscillation disappears via Hopf bifurcation at β ≈ 3.5).

Fig. 4.

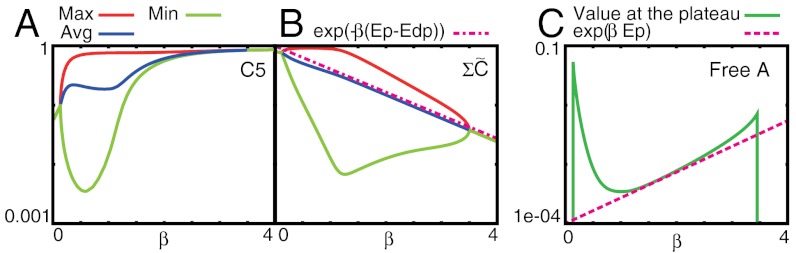
Normalized concentration of each component, C₅/C_total (A), 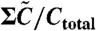(B), A/A_total (C) plotted against the inverse temperature β. (A and B) Maximum (red), minimum (green), and average (blue) over a cycle. (A) Note that the maximum value of C₅ is nearly constant, whereas its minimum and average increase with β beyond β_c (i.e., at lower temperature). (B) The average value of 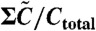is fitted well by the value of the unstable fixed point of the equation (magenta line), which is proportional to exp(-β(E_p - E_dp). (C) The concentration of free KaiA in the plateau region of C₅ is plotted, as estimated from the time where C₃ reaches a peak. This free KaiA concentration closely follows exp(βE_p) (magenta line), for β > β_c—i.e., below the critical temperature.

Proportion of Free-Energy of Phosphorylation to that of Dephosphorylation Is Critical for Temperature Compensation.

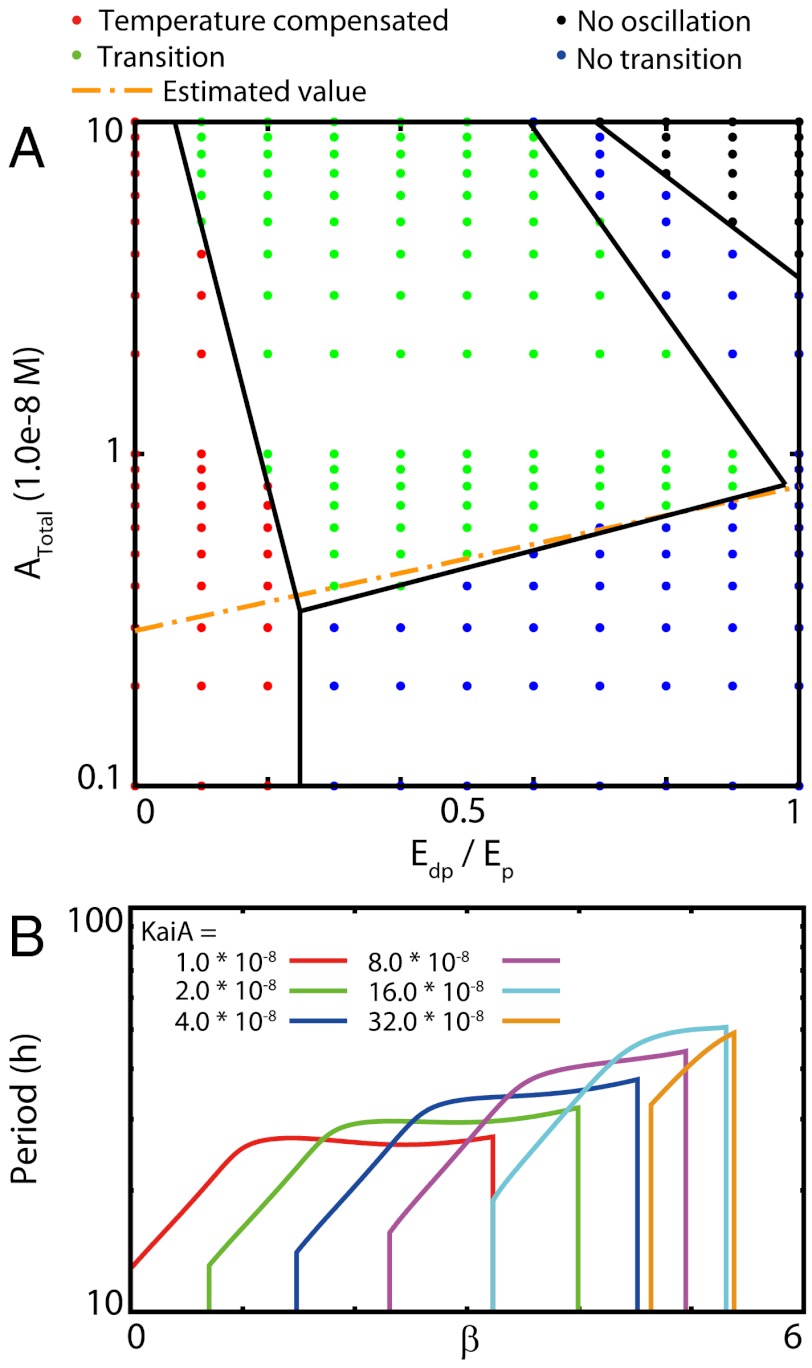
Thus, the transition in the oscillation and temperature compensation behavior at low temperature is the salient feature of the present system. Next, we analyzed the conditions for E_p and E_dp, the activation energies for phosphorylation and dephosphorylation, respectively, to elucidate the temperature compensation. SI Appendix, Fig. S4 shows a plot for the region where temperature compensation appears in the parameter space of E_p and E_dp. From SI Appendix, Fig. S4, we observe that temperature compensation appears in the regime E_p ≳ 5E_dp. The overall periodic behavior is determined mainly by E_dp/E_p, rather than the individual magnitudes. When 0.2 < E_dp/E_p < 1, there still exists a transition to a regime with weaker temperature dependence on lowering the temperature, but this effect is not sufficient to produce the temperature compensation (see also Fig. 5A). (See supporting information for the case with E_p < E_dp.)

Fig. 5.

Influence of activation energy difference and the KaiA abundance on the temperature dependence of the period. (A) Diagram of the temperature dependence of the cycle against activation energy ratio (E_dp/E_p) and abundance of total KaiA (A_total). Red: temperature-compensated oscillation with ∂τ/∂β ∼ 0 (τ: the period) below the critical temperature. Green: oscillation showing transition at the critical temperature. Blue: oscillation without transition, with a simple increase with temperature following the Arrhenius form. Black: no oscillations at all. Orange dotted line: transition line theoretically estimated from the condition at which the speeds of phosphorylation and dephosphorylation are equal. As E_dp/E_p increases from 0 to 1, we successively see temperature compensation, transition, and disappearance of oscillation. (For the case with E_p < E_dp, see SI Appendix.) As A_total increases, the width of the temperature compensation region decreases. (B) Effect of KaiA increase on the period. An increase in KaiA leads to narrowing of the range of the periodic solution and also the range of temperatures at which temperature compensation occurs.

Temperature Compensation Depends on Amounts of KaiA and KaiC.

As already mentioned by von Zon et al., oscillation of KaiC abundance requires that the amount of KaiA is less than that of KaiC (17). An increase in KaiA abundance leads to a decrease in the period, finally leading to no oscillations. The range of temperatures where oscillations exist narrows as KaiA abundance increases, and the oscillation disappears at higher temperatures. Here, the transition temperature T_c shifts to lower temperatures (see Fig. 5B). Furthermore, the temperature compensation at T < T_c is lost as KaiA abundance is increased. Although the temperature dependence of the period is weaker at T < T_c, the dependence exp(βΔE^′) still exists with ΔE^′ smaller than E_p. We plotted the range where temperature compensation occurs at T < T_c in the two-dimensional plane comprising KaiA abundances and E_dp/E_p. We see that a low level of KaiA abundance is necessary for temperature compensation. Note that when A_total is too small and E_p - E_dp is too large, temperature compensation is achieved without transition, because the phosphorylation process is rate limiting throughout the temperature region of interest. Note that temperature compensation emerges for a sufficiently broad range of values for parameters E_p and E_dp. This is free for other parameter values.

Range of Temperatures Where Systems Are Temperature-Compensated Is Narrowed by a Reduction in Phosphorylation Sites.

Because KaiC is a hexamer, we adopted six phosphorylation sites in our model. However, to understand the biological significance of this number of sites, we examine models with a reduced number of phosphorylation sites (SI Appendix, Fig. S6). We find that the reduction in the number of phosphorylation sites when moving from hexamer to pentamer, and then to tetramer, narrows the temperature range where oscillations exist and temperature compensation occurs. For the tetramer, temperature compensation is not observed even at T < T_c.

KaiC Phosphorylation Cycle Is Entrained by Temperature Cycles.

It has been demonstrated that KaiC’s phosphorylation cycle is entrained to external temperature cycle (10). To examine such entrainment, we cycle the temperature between β = 1.5 and 1.7 (i.e., within the temperature compensation region) periodically in time with a period close to that of the Kai system (27 h). Within about 10 cycles, the period of oscillation of the KaiC system is entrained with that of temperature, independently of the initial period of oscillation. Thus, entrainment to the temperature cycle is achieved (see SI Appendix, Fig. S7).

Discussion

Here we discuss how temperature compensation is achieved. As presented in Results, there are two stages: transition in the temperature dependence of the period, and complete temperature compensation of the period at lower temperature. As seen in Fig. 5A, the former requires that E_p is sufficiently larger than E_dp, which, as will be shown, means that the phosphorylation process is rate limiting. For the latter, the abundance of KaiA should be sufficiently small so that there is limited free KaiA that can be used for phosphorylation (i.e., competition for free KaiA). As will be shown below, the abundance of free KaiA decreases as the temperature increases, which compensates for the increase in the rate constant of the reaction.

1. Transition.

When there is a difference between the energy barriers for phosphorylation and dephosphorylation, the temperature dependence of the rate of each process is different. Roughly speaking, the time scale for the phosphorylation process changes in proportion to A exp(βE_p), whereas dephosphorylation has exp(βE_dp), where A is the concentration of free KaiA. Thus, there exists a critical temperature at which the two rates are comparable; the rate-limited reaction switches at this temperature, where the transition to temperature dependence occurs. Thus, β_c ≃ log A/(E_p - E_dp) where A, the concentration of free KaiA, is estimated from the steady-state solution of our model to afford A ≃ K₅A_total/(K₅ + C₅) if A_total ≪ K₅ and A ≃ A_total if A_total≫K₅.

Thus, a sufficient difference in activation energy is necessary for the transition-like behavior because the critical temperature will diverge as E_p ≃ E_dp. If the difference is small, the critical temperature goes below the temperature for the onset of oscillation and the transition never occurs. If A_total is too large or too small, the critical temperature is lower or higher than the range where the oscillation exists, and thus for both the cases, the transition disappears. These estimates are consistent with Fig. 5A.

2. Temperature Compensation by Autonomous Regulation of the KaiA Concentration.

As mentioned, the reaction from C₅ to C₆ becomes a bottleneck at lower temperature, and the amount of active and inactive KaiC is mainly determined via C₅ and 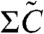. When the temperature is lower than the transition temperature, the phosphorylation process takes more time, and C₅ accumulates before dephosphorylation from C₆ progresses, as already discussed (see Fig. 2B). The increase in the abundance of active KaiC leads to competition for KaiA and thus a decrease in free KaiA. If the total KaiA abundance is limited, the system reaches a stage where phosphorylation almost stops. This leads to the plateau in the time course of C₅, as observed in Fig. 2B. This drastic slowdown of the phosphorylation process occurs when A is decreased to the level at K_pA ≲ 1. Thus, during the plateau in C₅, this approximate estimate gives A ∝ 1/K_p ∝ exp(βE_p). Thus, the temperature dependence of the phosphorylation rate K_pA is compensated for by the decrease in A. This plateau region is rate-limited in the circadian cycle, making the whole period independent of temperature.

In more detail, this compensation is also estimated as follows. The abundances of the inactive forms of KaiC decrease with an increase in C₅. Considering the differences in speed between phosphorylation and dephosphorylation, the total inactive KaiC abundance (at the fixed point) is estimated as

[5]

which is consistent with Fig. 4. The flow from inactive KaiC is thus estimated by .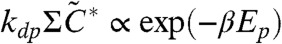

This flow starts the phosphorylation processes from C₀ but is slowed down at some number of phosphorylated subunits on the KaiC hexamer, m. In the present model, this slowdown starts at m ≈ 2 ∼ 3 due to the paucity of free KaiA. Following the above estimate of flow, the maximum C_m is estimated to be proportional to exp(-βE_p). Now from Eq. 4 and K_m ≪ K_i (i > m) and C_j ≪ C_m (j < m) at this time, the abundance of free KaiA can be estimated approximately as A ≃ A_total - (AC_m)/(K_m + A). When A_total is small enough, the minimum free KaiA abundance is smaller than K_m, thus A ≃ A_total - (AC_m)/(K_m).

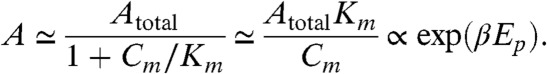[6]

Therefore, when A_total is small enough and E_p is sufficiently greater than E_dp, the time scale of the phosphorylation process is k_pA, and the period of the cycle is temperature-compensated. Indeed, as shown in SI Appendix, Fig. S3, the maximum C₁ (and C₂) values show exp(-βE_p) dependence, whereas free KaiA shows approximately exp(βE_p) dependence when phosphorylation is slowed down.

Below T_c, the process stops for a long time at the limited process, phosphorylation from C₅ to C₆. Hence, accumulation of C₅ occurs, which leads to a qualitative change in the amplitude.

In essence, the temperature compensation mechanism requires two properties: difference in activation energy between phosphorylation and dephosphorylation processes, and a limited abundance of enzyme KaiA. The former is essential to the transition, and the latter to the compensation for the Arrhenius-type temperature dependence of the individual reactions. As long as these conditions are met, the period is temperature-compensated at low temperature, without the need for fine tuning of the parameters of the system. This enzyme-limited competiton (ELC) mechanism is important for understanding temperature compensation.

These two properties generally appear if there are two types of processes with different activation energy, with one type catalyzed by a common enzyme and the other not being catalyzed by the common enzyme or at all. If the enzyme abundance is limited, the competition for the enzyme will lead to temperature compensation in cyclic reaction systems. In particular, if the main component of the chemical reactions has allosteric structure like KaiC, the competition for enzymes will occur naturally.

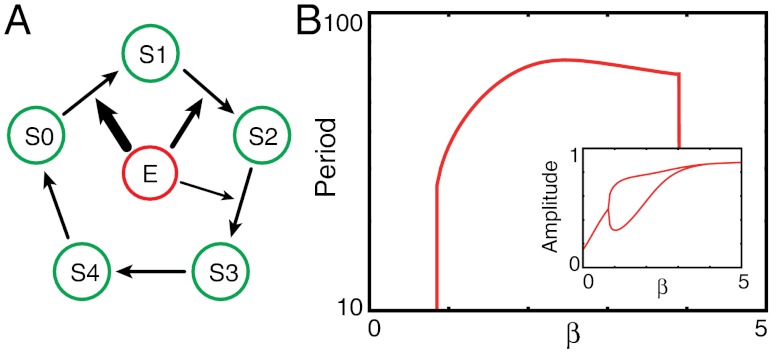
As an example, we consider the cyclic process shown in Fig. 6, where a cyclic change in five substrates occurs. Three processes, S₀ → S₁ → S₂ → S₃, have a high activation energy barrier and are catalyzed by the common enzyme E. In this case, the period of the oscillation in the concentration of each substrate is temperature-compensated at low temperature. If the number of reactions with the common enzyme is decreased to two, compensation still appears, but it is weaker, as shown in SI Appendix, Fig. S8. This example demonstrates the generality of the ELC mechanism and opens the possibility of applications to temperature compensation in other biochemical oscillations as well.

Fig. 6.

Temperature compensation of period in a simpler model with enzyme competition. (A) Scheme of the simpler model. The substrate has five forms, and reactions S₀ → S₁, S₁ → S₂, S₂ → S₃, S₃ → S₄ are catalyzed by the same enzyme E, but the other reactions are not. The affinity between S_i and E weaken as i increases. (B) The period, plotted against the inverse temperature β. The oscillation is temperature-compensated over a specific range of temperatures, although the transition is not as sharp as in the Kai model. (Inset: maximum and minimum values of S₂ over a cycle.)

Regulation of reaction speed by limitation of catalysts, as proposed here, should be important, not only for the temperature compensation of circadian clocks in general but also for other biological processes. For example, we expect that the ELC mechanism could work even for steady-state fluxes in an open flow system instead of a closed oscillation circuit, if a common enzyme is shared and competed for among several reactions (33, 34).

Recall that as a consequence of our mechanism, the temperature dependence of the rate of the reactions of interest is compensated for by the change in the concentration of the available enzyme. Hence, when our mechanism works, it may be observed that some “balance” also occurs. In this regard, in some systems that are so far regarded as being examples of the “balance mechanism,” it may in fact be the ELC mechanism that underlies the balance. By studying, in more detail, the dynamics of enzyme concentrations, our mechanism may be unveiled therein.

The regulation of reaction process by autonomous changes in enzyme concentration, as proposed here, was previously pointed out by Awazu and Kaneko, who reported that relaxation to equilibrium slows down when the concentrations of substrate and enzymes are negatively correlated (35). Excess substrate hinders the enzymatic reaction, leading to a plateau in relaxation dynamics. In the present model, the total concentration of KaiA as an enzyme is a conserved quantity but the fraction of free KaiA available is reduced when there is abundant active KaiC so that the speed of phosphorylation slows down dramatically. In this sense, several other Kai models that adopt competition for KaiA as a driving force for synchronization of each KaiC hexamer should fit well with our scheme. For example, our mechanism may work in the model by Mehra et al (28).

Now we briefly discuss the relevance of the present results to experiments on the Kai protein circadian system. In our model, it is assumed that KaiC’s affinity to KaiA depends on the phosphorylation levels. This assumption is necessary not only for the emergence of temperature compensation but also for the existence of the oscillation itself.

In the actual circadian clock comprising Kai proteins, KaiB is also involved besides KaiA and KaiC. However, as mentioned, an increase in KaiB abundance has minor influence on the clock (26). Earlier it was suggested that KaiB binds to KaiAC complexes strongly and restricts the concentration of free KaiA (17). Thus, the inclusion of KaiB is expected to not alter the present temperature compensation mechanism but to facilitate it by strengthening the limitation of enzyme availability. Note that previously reported temperature compensation at the element level—KaiC’s ATPase activity (4) and auto-dephosphorylation activity (19)—is also relevant to our model; the former to achieve fast equilibration between KaiA and the KaiA complex used for Eq. 4, and the latter to provide E_dp ≪ E_p.

It is known that the amplitude of KaiC oscillation decreases as the temperature is lowered (8), which agrees well with our results (Fig. 2A). Indeed, as described already, this decrease in amplitude is tightly coupled with the temperature compensation mechanism. It is also interesting to note that in many circadian clocks, the period does not depend on the temperature, although the amplitude decreases with temperature (8). If every elementary step of the circadian clock were temperature-compensated at the single-molecule level, this temperature dependence of the amplitude would not be possible. Furthermore, the entrainment of the KaiC oscillation to imposed temperature cycles, as observed in a recent experiment naturally appears without further tuning the model (10).

Our mechanism for temperature compensation depends on the paucity of KaiA-increasing the KaiA concentration leads to loss of compensation. We expect that this prediction will be directly confirmed in a future experiment.