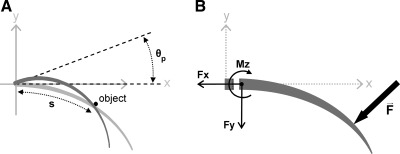
Fig. 3.
Key variables used to describe vibrissa mechanics. A: schematic of a vibrissa rotating against a point object. The arc length at which the vibrissa makes contact with the object, s, is represented as a fraction of the total arc length of the vibrissa. Rotations of the vibrissa against the object in the plane of rotation (in this example, the x-y plane) are indicated with theta push (θp). θp equals 0° at the angle at which the vibrissa first makes contact with the object. B: in the most general case, there will be 3 reaction forces and 3 reaction moments at the base of the vibrissa resulting from an applied force. If we assume that the intrinsic curvature of the vibrissa always lies in the plane of rotation, then this reduces to 2 reaction forces (axial force Fx and transverse force Fy) and 1 reaction moment (Mz) at the base. All variables are negative in the directions shown.