Abstract
Human color constancy has been studied for over one hundred years, and there is extensive experimental data for the case where a spatially diffuse light source illuminates a set of flat matte surfaces. In natural viewing, however, three-dimensional objects are viewed in three-dimensional scenes. Little is known about color constancy for three-dimensional objects. We used a forced-choice task to measure the achromatic chromaticity of matte disks, matte spheres, and glossy spheres. In all cases, the test stimuli were viewed in the context of stereoscopically viewed graphics simulations of three-dimensional scenes, and we varied the scene illuminant. We studied conditions both where all cues were consistent with the simulated illuminant change (consistent-cue conditions) and where local contrast was silenced as a cue (reduced-cue conditions). We computed constancy indices from the achromatic chromaticities. To first order, constancy was similar for the three test object types. There was, however, a reliable interaction between test object type and cue condition. In the consistent-cue conditions, constancy tended to be best for the matte disks, while in the reduced-cue conditions constancy was best for the spheres. The presence of this interaction presents an important challenge for theorists who seek to generalize models that account for constancy for flat tests to the more general case of three-dimensional objects.
Introduction
Color constancy is classically conceived as the ability to perceive stable object colors, despite variation of illumination and scene context. Such constancy is difficult to achieve because the light reflected from objects varies with the illumination. Given that there is considerable variation in the spectral and spatial properties of natural illuminants, constancy helps object color to be a useful guide to object identity.
Many studies of color constancy have examined the color appearance of diffusely-illuminated flat matte surfaces (e.g., Helson & Jeffers, 1940; Helson & Michels, 1948; McCann, McKee, & Taylor, 1976; Arend & Reeves, 1986; Brainard & Wandell, 1992; Brainard, Brunt, & Speigle, 1997; Brainard, 1998; Kraft & Brainard, 1999; Delahunt & Brainard, 2004; Granzier, Brenner, Cornelissen, & Smeets, 2005; Olkkonen, Hansen, & Gegenfurtner, 2009). Taken as a whole these studies reveal that under many conditions the human visual system exhibits considerable constancy, and some of the computations and mechanisms that support such constancy have been delineated (reviews in Brainard, 2004; Brainard & Maloney, 2011; Foster, 2011).
Constancy has also been studied for flat matte surfaces viewed in spatially rich three-dimensional scenes. Embedding stimuli in three-dimensional scenes allows one to study the effect of three-dimensional surface pose on perceived surface lightness and color (Bloj, Kersten, & Hurlbert, 1999; Boyaci, Maloney, & Hersh, 2003; Ripamonti et al., 2004; Boyaci, Doerschner, & Maloney, 2004; Werner, 2006; see also Hochberg & Beck, 1954; Gilchrist, 1977; Gilchrist, 1980), as well as the effect of cues to the illuminant (e.g. specular highlights on surrounding objects, mutual illumination between surfaces) that are not available when all surfaces in the scene are flat, co-planar, and matte (Yang & Maloney, 2001; Yang & Shevell, 2003; Kraft, Maloney, & Brainard, 2002; Doerschner, Boyaci, & Maloney, 2004; see also Lee, 1986; Tominaga & Wandell, 1989; Funt & Drew, 1988). Some theoretical approaches to understanding the effects of three-dimensional geometry for flat test surfaces are available (Gilchrist et al., 1999; Gilchrist, 2006; Brainard & Maloney, 2011).
In natural scenes, however, only a small fraction of objects are flat and matte. Indeed, the reflectance of most real objects must be characterized as a function of the direction of incident and reflected light rays. Such a characterization is called the object’s bidirectional reflectance distribution function (BRDF). Object BRDFs vary according to what the object is made from: different materials such as plastic, metal, wax, and fabric have different BRDFs. How the material properties of three-dimensional objects interact with their perceived lightness and color, as well as how we perceive the material properties of objects, is receiving increased attention (Blake & Bülthoff, 1990; Pessoa, Mingolla, & Arend, 1996; Nishida & Shinya, 1998; Fleming, Dror, & Adelson, 2003; Todd, Norman, & Mingolla, 2004; Fleming & Bülthoff, 2005; Motoyoshi, Nishida, Sharan, & Adelson, 2007; Xiao & Brainard, 2008; Sharon, Li, Motoyoshi, Nishida, & Adelson, 2008; Olkkonen & Brainard, 2010; Olkkonen & Brainard, 2011; Marlow, Kim, & Anderson, 2011; Kim, Marlow, & Anderson, 2011).
Little is known about the color constancy of three-dimensional objects, particularly those made of non-matte materials (but see Hedrich, Bloj, & Ruppertsberg, 2009; de Almeida, Fiadeiro, & Nascimento, 2010; Olkkonen & Brainard, 2010; Olkkonen & Brainard, 2011). Here we report experiments that address this issue. We used a forced-choice procedure to determine the chromaticities at which matte and glossy spheres, embedded in three-dimensional scenes, appeared achromatic. We also determined such achromatic chromaticities for flat matte disks embedded in the same scenes. We varied the scene illuminant and the reflectance of the surface immediately behind the tests, and used the results to determine constancy indices.
A focus of the experiments is the question of whether the constancy found for three-dimensional spheres bears a simple relation to the constancy found for flat matte tests. More specifically, we asked whether there is an interaction between the test object’s three-dimensional shape and spectral changes in the contextual scene. Answering this question is key to determining whether extant theories of constancy, developed for flat matte tests, may be easily generalized to handle three-dimensional objects.
Experiment 1
Methods
Apparatus
Stimuli were presented to observers stereoscopically using two CRT monitors (Hewlett-Packard, Palo Alto, CA, Model p1230). The monitors were driven at a 75 Hz refresh rate at 1152 by 870 spatial resolution, and with a color lookup table providing 14-bit (pseudo-color) resolution for each color channel (BITS++, Cambridge Research Systems, Rochester, England). Two small mirrors were placed directly before the observers. The mirrors reflected the images displayed on the left and right monitors to the left and right eyes. Observers viewed the monitors through two square apertures, one for each eye. Black posterboard and black cloth were used liberally to minimize stray light reaching the observer.
We used custom software to align the images from the two monitors. The mirrors in the display were temporarily replaced by beam splitters, allowing a common reference grid to be visually superimposed with each monitor. An observer manually positioned a dot displayed on each monitor to align with each grid intersection. We used the positions of the aligned dots to determine transformations between image and monitor coordinates, so that during the experiment each displayed image was mapped to the grid-aligned coordinate system. The distance from the cyclopean eye to the alignment grid was 76.4 cm. This was also the approximate optical distance of each monitor to the corresponding eye.
Stimulus Scenes
The stimuli consisted of graphics simulations of illuminated scenes. The geometry of the scenes was created using the Maya software tools (Alias, Inc., San Rafael, CA). They were rendered using the Radiance package (Ward, 1994; http://radsite.lbl.gov/radiance/HOME.html), augmented by custom Matlab tools (Render Toolbox; http://rendertoolbox.org) that allowed us to specify spectral surface reflectance functions and illuminant spectral power distributions (400-700 nm at 10 nm intervals) as well as to render on a wavelength-by-wavelength basis. This process resulted in a 31-plane hyperspectral image of each scene. The hyperspectral images were converted to three-plane LMS representations by computing at each pixel the excitations that would be produced in the human L-, M- and S- cones. We used Stockman-Sharpe cone fundamentals for this calculation (Stockman & Sharpe, 2000; CIE, 2007).
Scenes were rendered from two viewpoints, corresponding to the positions of the observer’s two eyes (6 cm horizontal separation). Each eye received the image rendered from the corresponding viewpoint.
Each scene contained a test object whose color appearance was judged by observers. The test object could be a flat matte disk, a matte sphere, or a glossy sphere. These three test objects are illustrated by the images shown in the top row of Figure 1.
Figure 1.
Examples of experimental images. The three images in the top row show the experimental scene rendered using the Neutral illuminant. Across these three images, the test object varies. Left: matte disk; center: matte sphere; right: glossy sphere. The three images in the bottom row show the rendered scene for the Yellow illuminant consistent-cue condition (left), Blue illuminant consistent-cue condition (center), and Blue illuminant reduced-cue condition (right). The images shown in the figure were converted from the LMS cone representation to the sRGB color space for display. They were also tone mapped using an automated procedure that scaled each image so that its maximum luminance value was five times the image mean and then clipped out-of-range pixels. This tone mapping procedure differs from that applied to the experimental images and was used here for convenience.
The rest of the scene provided the context in which the test object was viewed. The immediate surround of the test object consisted of a spatially uniform background on the back wall of the rendered scene. The global surround was provided by a checkered pattern on the remainder of the back wall and floor of the scene, as well as by four contextual spheres (see Figure 1). A summary of key scene parameters is provided below.
We specify xyz scene coordinates in cm relative to an origin defined by the position of the cyclopean eye of the observer. The x coordinate decreases to the observer’s left and increases to the right; the y coordinate decreases in the down direction and increases in the up direction; the z coordinate increases with increasing distance from the observer. In this coordinate system, the center of the test objects was located at (0.2, 2.3, 72.1) cm and the diameters of the test objects were 3.3 cm (disks) and 3.2 cm (spheres).
The center of the spatially uniform region background behind the test object was located at (0.4, 2.1, 76.3) cm and had xy dimensions of 10.8 by 11.7 cm. The floor was located at a y coordinate of −6 cm. The four contextual spheres all had diameter 3.2 cm and had centers located at (clockwise from upper left) (−4.7, 6.7, 74.7), (5.7, 6.5, 66.4), (4.8, −3.8, 74.2), and (−4.1, −4.4, 67.3) cm. The front wall of the scene was at a z coordinate of 55.4 cm. It contained an aperture through which the scene was visible. The xy center position of the aperture was (0.0, 0.0) cm and its xy size was 15.2 by 13.5 cm. Not visible through the aperture were side walls at x positions of −16.6 and 16.9 cm and a ceiling at a y position of 27.8 cm. The interior of the front wall, the side walls, and the ceiling all had the same spatially uniform reflectance.
The geometric surface reflectance properties of all objects in the scenes were specified with respect the isotropic Ward reflection model (Ward, 1992), as implemented in Radiance using its plastic material type. The RenderToolbox allowed us to vary the diffuse reflectance component of objects as a function of wavelength; the non-diffuse (specular) reflectance component was constant as a function of wavelength. In Experiment 1, all surfaces were matte (diffuse reflectance only), except for the glossy test sphere. The Ward model parameters for non-diffuse reflectance component of this sphere were 0.02 (gloss parameter) and 0.00 (roughness parameter) at all wavelengths. No correction was made for the fact that before rendering, Radiance applies a normalization to the magnitude of the specified diffuse reflectance component of glossy objects, so that the diffuse component of the matte and glossy test objects varied slightly in overall magnitude. The diffuse spectral reflectance functions of the contextual surfaces in the scene are provided in the supplemental material.1 These were held fixed across conditions, with the exception of the uniform surface that provided the immediate background for the test object. This was varied according to condition as described in more detail below.
Each scene was illuminated by four area light sources and one diffuse light source. The area lights were parallel to the floor of the scene and each had xz extents of 4 cm by 4 cm. The center coordinates of the four area lights were (7.0, 26.0, 77.4), (−7.0, 26.0, 77.4), (7.0, 26.0, 57.9), (−7.0, 26.0, 57.9) cm. For each illuminant condition, all light sources shared the same spectrum. Three illuminant spectra were used. The Neutral illuminant was CIE daylight D65 (CIE, 2004). The Blue and Yellow illuminants were constructed from the CIE linear model for daylights (Judd, MacAdam, & Wyszecki, 1964; CIE, 2004). The Blue illuminant had a correlated color temperature of 15000K and the Yellow illuminant had a correlated color temperature of 3500K. The spectra of these illuminants are provided in the supplemental material. Scenes rendered under the Yellow and Blue illuminants are shown in the bottom row of Figure 1 (left and center images).
The illuminant intensities were specified in arbitrary units. The resulting images were then scaled by a common (across conditions) factor to bring them into the general intensity range of our monitors. To characterize the overall intensity of each scene, we measured the mean pixel luminance values of the uniform background surface behind the test object. These values are provided in the supplemental material, as part of the data tabulated for each individual observer.
To examine the role of local contrast on constancy, we studied both consistent-cue and reduced-cue conditions. In the consistent-cue conditions, only the illuminant was varied, while the contextual surfaces in the scene remained fixed. In the reduced-cue conditions, we co-varied the simulated reflectance of the central patch of the background wall with the illuminant, so as to hold the light reflected from that part of the wall constant. This manipulation tends to reduce constancy (Brainard, 1998; Kraft & Brainard, 1999; Delahunt & Brainard, 2004) and can provide data diagnostic for testing models of constancy (Brainard et al., 2006; Brainard & Maloney, 2011). We refer to the immediate background of the test object in the consistent-cue conditions as the normal background; we refer to the immediate background of the test object in the reduced-cue condition as the equated background. The reflectance functions used for the background central patch for each condition are provided in the supplemental material. The center and right images in the bottom row of Figure 1 illustrate the difference between consistent-cue and reduced-cue conditions.
Because some of the rendered images had a high-dynamic range, it was necessary to tone-map the images after the overall scaling described above had been applied. We used a simple tone-mapping procedure that truncated pixel luminance to 25 cd/m2 while holding the chromaticity of each truncated pixel constant.
The scaled and tone-mapped LMS images were converted for display using standard methods that accounted for the spectral power distributions of the monitor’s phosphors and for the monitor’s gamma functions (Brainard, Pelli, & Robson, 2002).
Due to a bug in the experimental software, the images were displayed on the experimental monitors at 80% of their intended size. (This bug was corrected for Experiment 2.)
Manipulation of test object color
To vary the cone coordinates of the test objects without full re-rendering of the scene, we pre-rendered each test object with eight basis surface reflectances. We could then recombine the pre-rendered images at run time to produce test objects with any desired colorimetric coordinates (see Xiao & Brainard, 2008; also Griffin, 1999). The reported xy chromaticities and luminances of test objects were obtained by taking the spatial average of the Judd-Vos (Vos, 1978) XYZ tristimulus coordinates of the pixels in the image of the object.
Summary of Conditions
There were two shapes for the test object (sphere and disk). For the spheres, there were two materials, matte and glossy. For each test object, there were five contextual conditions (Neutral, consistent-cue Blue, consistent-cue Yellow, reduced-cue Blue and reduced-cue Yellow).
Task
A single condition was studied in each experimental session, with multiple sessions typically run on each day with short breaks between sessions. Observers ran in at least one practice session to become familiar with the experimental procedures before starting on experimental sessions.
We used a forced choice procedure to determine the LMS coordinates of test objects that appeared achromatic (Chichilnisky & Wandell, 1999). At the start of an experimental session, observers were presented with a scene of an empty room and initiated a block of trials by pressing a button. On each trial a test object appeared for 0.75 seconds in the scene and then disappeared, and observers performed one of two forced choice tasks. On red-green trials, observers pressed one button if the test object appeared reddish, and another if it appeared greenish. On blue-yellow trials, observers pressed one button if the test appeared bluish and another if it appeared yellowish. The two types of trials were interleaved in blocks of seven trials each. At the beginning of each block, a speech synthesizer announced the trial type for the next seven trials. We discarded the first trial after each staircase-type switch to minimize contamination caused by observer confusion about which judgment was being performed. An experimental session consisted of 15 blocks of each trial type (180 non-discarded trials per session).
Across blocks, the trials were organized into red-green and blue-yellow staircase pairs that sought the achromatic point for the test object. Three staircases pairs were run in each session, each with a different randomly chosen starting point (see below). Each member of a staircase pair consisted of 30 trials, for a total of 180 non-discarded trials per session. Within each block, two trials were run for the corresponding member of each of the three staircase pairs. The order of trials for the three staircase pairs was randomized in subblocks of three trials each.
The procedure for each staircase pair is most easily understood by reference to Figure 2A, which shows data from one staircase pair in an r,b chromaticity space defined with respect to the monitor primaries. Let R, G, and B represent the linear weights of each monitor primary required to produce the average LMS coordinates of the test object. Then
Specification of the r,b coordinates of the test object, together with its luminance, is sufficient to reconstruct the average LMS coordinates of the test object and vice-versa. The average luminance of the test objects was held constant at 5 cd/m2.
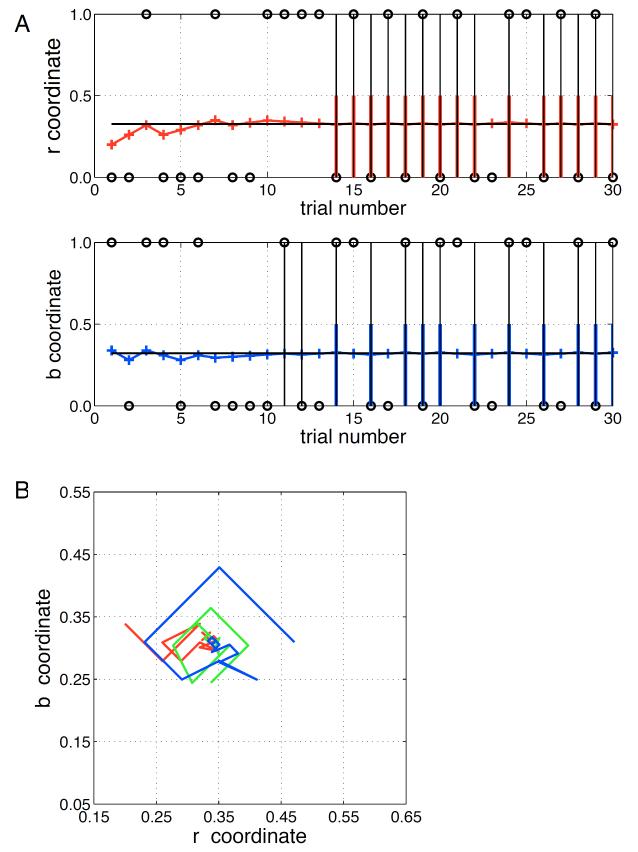
Figure 2.
A) Data from one staircase pair (observer SXT, matte disk, Neutral illuminant). The top plot shows the test object r value on every red-green trial while the bottom plot shows the test object b value on every blue-yellow trial. Open circles indicate the observer’s response on each trial (a circle plotted at 0 indicates green and yellow responses, while a circled plotted at 1 indicates red and blue responses). Vertical black lines extending between 0 and 1 indicate reversals at the smallest step size. Vertical colored lines extending between 0 and 0.5 indicate reversals averaged in computation of achromatic point for this staircase pair. Both staircases had to have reached the smallest step size before reversals for either staircase were averaged. In applying this criterion, we neglected effects of trial-type blocking and took as concurrent trials from each staircase type that had the same trial number within their respective staircases. B) Trajectory of the three staircase pairs from one session. Same session as for staircase pair shown in A. Each colored line indicates the trajectory of r,b chromaticities for one staircase pair. The b value for each trial of the b staircase is plotted against the r value for the corresponding trial of the r staircase. Because the two trial-types were interleaved in blocks, these are not the exact r,b chromaticities shown on any particular trial; the trajectories shown, however, provide a visual sense of the progression of each staircase pair. The closed circles indicate the r,b chromaticity of the achromatic locus determined from each staircase pair, and the black square shows the average taken over the three staircases.
To initialize each staircase pair, r,b coordinates were chosen according to a uniform pseudorandom distribution within the range [0,1]. If the result corresponded to RGB coordinates for the test object that were within the monitor gamut, the chosen r,b coordinates were used as the starting point for the staircase pair. If not, new r,b coordinates were drawn and the process repeated until a within-gamut starting point was found. Once initialized, the observer’s responses were used to modify the r and b values of the test object. On red-green trials, a reddish response led to a decrease of the r chromaticity of the test object while the b value was left unchanged; a greenish response led to an increase of the r value, again with the b value unchanged. On blue-yellow trials a blue response led to a decrease of the b value with the r value unchanged and a yellowish response led to an increase of the b value with the r value unchanged. The initial step size of the adjustments was 0.06 for both r and b. After the second reversal, the step size decreased to 0.03. After the fourth reversal, it decreased again to 0.014. A final decrease to 0.006 occurred after the fifth reversal. Thereafter, the adjustment step size was held constant. For each staircase pair, the r and b coordinates of the achromatic point were obtained from the corresponding staircase of the pair. These were taken as the mean of all reversals when both staircases had reached the smallest step size. We took the r/b value for a reversal to be the average of the value on the reversal trial and on the preceding trial.
Figure 2A shows the data for one staircase pair from one session. Note the decrease of step size at several of the reversal points, and that the staircases converge well before the 30th trial. Figure 2B plots the trajectories of all three staircase pairs from this session. Note that although the staircases begin at different points in the r,b chromaticity space, they converge to a common point.
Although the staircases generally converged well, we implemented procedures to exclude bad staircase pairs and sessions. First, to verify that a staircase pair had converged we required that both staircases in a pair had reversed at least once after each had reached its smallest step size. Staircase pairs that did not meet this convergence criterion were dropped. To include data from a session we required that at least two of the staircase pairs within that session converged by the above criterion. For such sessions, we took the r and b values of the achromatic point to be the mean r and b values from the staircase pairs that had converged. If the within session standard deviation for either the r or b values from the staircase pairs that had converged exceeded 0.02, we excluded the data from that session from further analysis.
Observers
Three naïve observers (TYD, female, age 18 years; YRT male, 19 years; SXT female, 22 years; FJK female, 20 years) completed the experiment. Each had corrected Snellen acuity of 20/30 or better in both eyes, normal color vision as assessed by the Ishihara plates (Ishihara, 1977; no more than 2 plates incorrect), and normal stereo vision as assessed by the Keystone VS-II Model 1135A vision screening system (no more than 1 incorrect response). For observer FJK, however, we discovered at the end of the experiment that the latter 2/3 of her sessions failed to meet our inclusion criteria. This observer’s data are not included in the analyses presented in the paper, but for completeness are available in the supplemental material. Two additional observers started the experiment. One was discontinued after running in three experimental sessions because his staircases did not reliably converge. The other was discontinued after running in nine experimental sessions for failing to reliably appear for scheduled experimental sessions. Data from these two observers was not analyzed further.
Each observer completed three sessions for each experimental condition (test object, illuminant, and cue-condition), with one exception. Due to experimenter error, observer SXT completed four sessions for the matte disk/blue illuminant/equated background condition and two sessions for the matte sphere/blue illuminant/equated background condition. After application of our exclusion criteria, data from at least two sessions were available for all conditions for all observers.
Prior to experimental sessions for which data were recorded, each observer ran in one practice session (matte disk, neutral illuminant). Data from this session were not analyzed.
The experimental procedures conformed to the tenets of the Declaration of Helsinki.
Instructions
Observers were instructed as to the experimental procedures and the perceptual judgments they would be asked to make. The instructions emphasized that we wanted observers to judge the surface properties of the test objects, along the lines of the ‘paper instructions’ used by Arend and Reeves (1986). The full instructions provided to observers are available as part of the supplemental material.
In order to familiarize observers with the type of appearance judgment we wanted them to make, observers went through an induction procedure (Doerschner, Boyaci, & Maloney, 2007; Allred & Brainard, 2009) prior to receiving the experimental instructions. Here observers viewed a grayscale test cube placed in an illuminated chamber. Subjects were asked to match the paint of the test surface on the cube to that of a patch on a grayscale palette seen in an adjoining chamber. Observers were asked to make such matches for two additional cubes, with two other grayscale surface colors. After the matches were done, observers were allowed to handle three test blocks for up to two minutes. They then performed an additional short series of grayscale paint matches. The induction procedure was used to familiarize the observer with judging the appearance of object surfaces, and the responses were not analyzed. Additional details about the induction procedure are available as part of the supplemental material.
Results
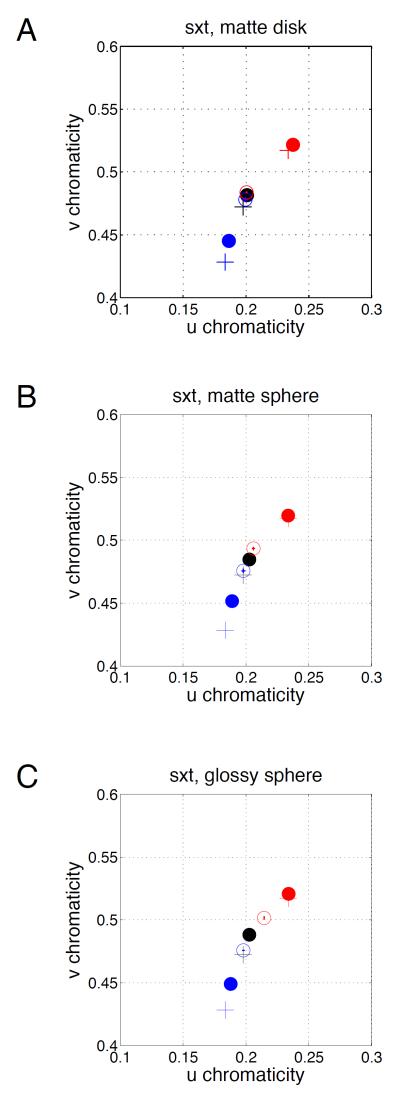
For all three test objects, constancy was good for the consistent cue condition. This is shown for Observer SXT by the filled circles in each panel of Figure 3, which show the achromatic chromaticities for the consistent-cue conditions (the three panels show data for the disk, matte sphere, and glossy sphere respectively.) Between the Neutral condition and the consistent-cue Blue and Yellow conditions, the achromatic chromaticities approximately track the changes in illuminant chromaticities (shown in the figure by the crosses). This is the pattern we expect in the data for a color constant visual system (Brainard, 1998; Delahunt & Brainard, 2004).
Figure 3. Achromatic chromaticies, Experiment 1, Observer SXT.
A) Matte disk. Plus symbols represent illuminant chromaticities. Solid circles represent consistent-cue condition achromatic chromaticities. Open circles represent reduced-cue achromatic chromaticities. Error bars are +/1 one SEM. Black symbols are for Neutral illuminant, blue symbols are for Blue illuminant and red symbols are for the Yellow illuminant. B, C) Matte sphere and glossy sphere respectively. Same format as A). Plots in the same format for the other observers, as well as tabulated individual observer data, are provided in the supplemental material.
In the reduced-cue conditions, constancy was much reduced. This is shown for Observer SXT by the open circles in each panel of Figure 3, which show the achromatic chromaticities for the reduced-cue Blue and Yellow conditions. These chromaticities lie much nearer to that of the Neutral illuminant than for the corresponding consistent-cue data and indicate a smaller degree of constancy. This observation is in accord with previous studies (Brainard, 1998; Kraft & Brainard, 1999; Delahunt & Brainard, 2004).
We used the achromatic chromaticities to compute a constancy index for each illuminant change and condition (see Delahunt & Brainard, 2004). The index takes on a value of 1 for perfect constancy and a value of 0 for no constancy, and is computed as follows. First, we used the achromatic chromaticity for the Neutral condition together with the spectral power distribution of the Neutral illuminant to compute an equivalent achromatic surface reflectance function. This is a surface reflectance function whose chromaticity under the Neutral illuminant matches the achromatic chromaticity. We then used the equivalent achromatic surface reflectance function to compute an equivalent illuminant spectral power distribution for each additional condition, so that the chromaticity of the equivalent achromatic surface reflectance function under the equivalent illuminant matched the measured achromatic chromaticity for each condition. We then found the uv chromaticity of the equivalent illuminant and computed the constancy index as:
where uveq is a vector specifying the CIE u’v’ chromaticity of the equivalent illuminant, uvillum is a vector specifying the chromaticity of the changed (i.e. either Blue or Yellow) illuminant, and uvneutral is a vector specifying the chromaticity of the Neutral illuminant. In computing the equivalent achromatic surface reflectance function and equivalent illuminants, we used three-dimensional linear models for surface and illuminant spectral power distributions. The surface linear model was computed from measured surface reflectance functions of the Munsell papers (Newhall, Nickerson, & Judd, 1943; Nickerson, 1957) and the illuminant linear model was the CIE daylight model (CIE, 2004). Because they are computed from the equivalent illuminants, our constancy indices are largely insensitive to any overall shifts in appearance with test object shape that occur within the Neutral illuminant condition and thus allow us to focus our attention on constancy with respect to our contextual manipulations.
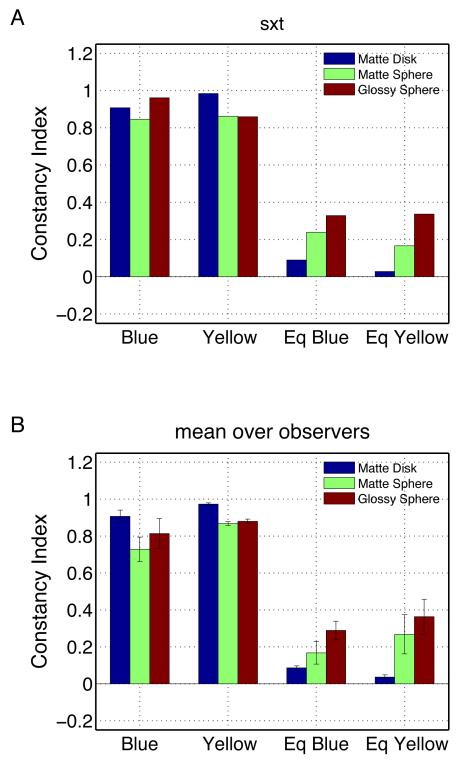
Figure 4A shows the constancy indices for Observer SXT, computed from the achromatic chromaticities shown in Figure 3. Figure 4B shows the mean constancy indices for all three observers. Several features of the data emerge from the constancy indices. First, the indices capture the good constancy for the consistent-cue conditions and decreased constancy for the reduced-conditions that was apparent in the achromatic chromaticities shown in Figure 3.
Figure 4. Constancy indices, Experiment 1.
A) Constancy indices for Observer SXT. Each group provides indices for one condition. Within group, the three bars provide indices for the matte disk, matte sphere, and glossy sphere. Blue: Blue illuminant change, consistent-cue; Yellow: Yellow illuminant change; consistent-cue; Eq Blue: Blue illuminant change, reduced-cue; Eq Yellow: Yellow illuminant change, reduced-cue. Constancy index plots for the other observers are available as part of the supplemental material. B) Mean constancy indices. Same format as A). Error bars show +/− 1 SEM.
Second, there is an interaction between test object type and constancy. For the consistent-cue conditions constancy is best for the matte disk, while for the reduced-cue conditions constancy is worst for the matte disk. While modest in size, the effects of test object are statistically significant (see Table 1). Examination of the pattern of variation in the indices suggests that the change from matte disk to matte sphere interacts with cue condition and that there is an improvement of constancy with change from matte sphere to glossy sphere. The improvement of constancy with the addition of specular highlights is consistent with previous reports (Yang & Maloney, 2001; Yang & Shevell, 2003).
Table 1. ANOVA for Experiment 1.
Observers were coded as a random variable. The main effect of each variable and the two-way interactions between all variables except observer were modeled.
| Source | VarType | SumSq | df | MeanSq | F | p |
|---|---|---|---|---|---|---|
| Observer | random | 0.04 | 2 | 0.02 | 2.52 | n.s. (0.10) |
| Test Object | fixed | 0.05 | 2 | 0.03 | 3.26 | n.s. (0.06) |
| Cue-Condition | fixed | 3.93 | 1 | 3.93 | 469.3 | < 0.001 |
| Illuminant | fixed | 0.04 | 1 | 0.04 | 4.68 | < 0.05 |
| Test Object*Cue-Condition | fixed | 0.22 | 2 | 0.11 | 13.25 | < 0.001 |
| Test Object*Illuminant | fixed | 0.02 | 2 | 0.01 | 1.13 | n.s. (0.34) |
| Cue-Condition*Illuminant | fixed | 0.01 | 1 | 0.01 | 0.65 | n.s. (0.43) |
| Error | random | 0.2 | 24 | 0.01 | ||
| Total | 4.51 | 35 |
Experiment 2
Purpose
The interaction between cue-condition and test object found in Experiment 1 is important, since such an interaction means that generalizing results obtained with flat tests to constancy for three-dimensional objects cannot be accomplished simply by measuring the effect of object shape on color appearance under a single illuminant. The main purpose of Experiment 2 was to determine whether this effect replicated with a new set of observers, and to explore the effect of other stimulus manipulations. In particular, an important difference between the disk and matte sphere is that the disk was essentially homogeneous in its luminance, while there was luminance variation across the sphere. In addition, the test luminance used in Experiment 1 was very close to that of the immediate surround which reduced the visibility of the border dividing the background from the matte disk. We manipulated test luminance in Experiment 2 to determine whether the effect of shape could be mimicked by overall test luminance variation and to include a condition where the background-disk border was not close to isoluminant. We also explored the effect of adding specular highlights to the contextual spheres. Since in Experiment 1 the effect of illuminant change was small and since there were no interactions with the illuminant (Table 1), in Experiment 2 we studied only the Blue illuminant change.
Methods
The methods for Experiment 2 were the same as those for Experiment 1 with the following changes.
Only the Blue illuminant change was studied.
Test luminances of both 3 cd/m2 and 5 cd/m2 were used.
A condition in which the contextual spheres were glossy rather than matte was added. The Ward parameters for these spheres matched those of the glossy test sphere: glossiness 0.02, roughness 0.00. This condition was run only for the 5 cd/m2 tests.
The software bug noted in the methods for Experiment 1 was fixed, so that the rendered images were displayed at their intended size.
Five new naïve observers participated (VJC, female, age 23 years; DYW, male, age 30 years; JOP, male, age 24 years; HBP, female, 24 years; UOS, female, age 18 years). Each had corrected Snellen acuity of 20/40 or better in both eyes, normal color vision as assessed by the Ishihara plates (Ishihara, 1977; no more than 2 plates incorrect), and functional stereo vision as assessed either by the Keystone VS-II Model 1135A vision screening system (no more than 1 incorrect response) or by a custom program run on our apparatus, in which they discriminated whether a square defined by binocular disparity appeared in front of or behind a spatially uniform background. One additional observer ran in six experimental sessions but was discontinued because her staircase data did not reliably converge. Data from this observer were not analyzed further.
The number of trials per staircase was reduced to 20, and the number of target sessions per condition reduced from 3 to 2. The experimenter examined the staircase convergence after each session, and re-ran a session if she judged that the within-session staircases had not converged to approximately the same achromatic point. We subsequently implemented our session exclusion criteria (see Methods for Experiment 1), and applied these to all sessions run. As a result of the exclusion, there were some conditions where only a single session of data were available for an observer. In addition, there were no good sessions for Observer JOP for the matte disk test at 3 cd/m2 for either the consistent-cue or reduced-cue conditions.
Results
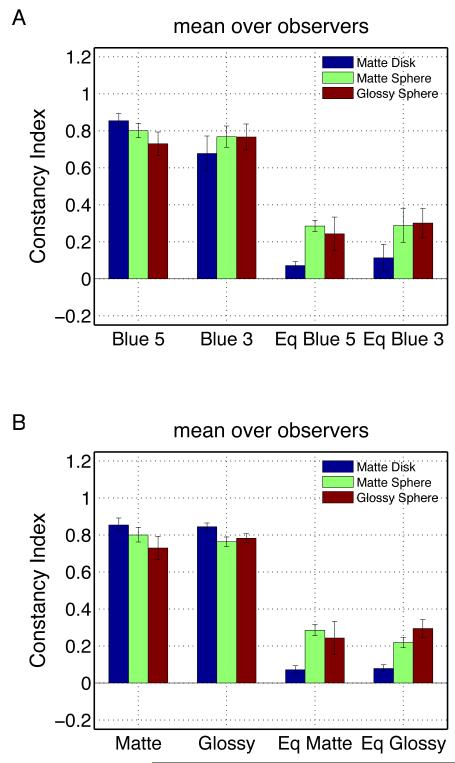
Figure 5A shows the constancy indices for both test luminances from Experiment 2 for the case where the contextual spheres were matte (as they were in Experiment 1). There was no significant effect of test luminance, nor did test luminance interact with the effect of test object or background (Table 2). For the 5 cd/m2 tests the pattern of results for the matte disk and matte sphere replicate what was found from Experiment 1 (see Figure 4). For the 3 cd/m2 tests, however, constancy for the matte disk was not better than that for the spheres in the consistent-cue condition. In addition, for both test luminances, there was no improvement in constancy between the matte and glossy spheres. What is robust across the two experiments is the improvement in constancy for the reduced-cue conditions between the matte disk and the spheres, and the data for Experiment 2 taken as a whole reveal a significant interaction between test object shape and cue condition (Table 2).
Figure 5. Constancy indices, Experiment 2.
A) Mean across observer constancy indices for Experiment 2 for conditions with matte contextual spheres for both test luminances. Within group, the three bars provide indices for the matte disk, matte sphere, and glossy sphere. Blue 5: Blue illuminant change, consistent-cue, 5 cd/m2 test. Blue 3: Blue illuminant change, consistent-cue, 3 cd/m2 test. Eq Blue 5: Blue illuminant change, reduced-cue, 5 cd/m2 test; Eq Blue 3: Blue illuminant change, reduced-cue, 3 cd/m2 test. B) Mean constancy indices for Experiment 2 with 5 cd/m2 tests for both matte and glossy contextual spheres. Within group, the three bars provide indices for the matte disk, matte sphere, and glossy sphere. Matte: Blue illuminant change, consistent-cue, matte contextual spheres. Glossy: Blue illuminant change, consistent-cue, glossy contextual spheres. Eq Matte: Blue illuminant change, reduced-cue, matte contextual spheres. Eq Glossy: Blue illuminant change, reduced-cue, glossy contextual spheres. Note that the data plotted for Matte and Eq Matte in B) are the same data plotted for Blue 5 and Eq Blue 5 in A. Error bars in both panels show +/− 1 SEM. The supplemental materials provide tabulated data for the individual observers, achromatic chromaticity plots for each observer, and constancy index plots for each observer.
Table 2. ANOVA for Experiment 2, matte contextual spheres, both test luminances.
Observers were coded as a random variable. The main effect of each variable and the two-way interactions between all variables except observer were modeled. Data are for the two test luminances and the matte contextual spheres.
| Source | VarType | SumSq | df | MeanSq | F | p |
|---|---|---|---|---|---|---|
| Observer | random | 0.39 | 4 | 0.1 | 7.09 | < 0.001 |
| Test Object | fixed | 0.1 | 2 | 0.05 | 3.74 | < 0.05 |
| Cue-Condition | fixed | 4.4 | 1 | 4.4 | 322.6 | < 0.001 |
| Target Lum | fixed | 0 | 1 | 0 | 0.08 | n.s. (0.79) |
| Test Object*Cue-Condition | fixed | 0.12 | 2 | 0.06 | 4.34 | < 0.05 |
| Test Object*Target Lum | fixed | 0.03 | 2 | 0.01 | 0.96 | n.s. (0.39) |
| Cue-Condition*Target Lum | fixed | 0.03 | 1 | 0.03 | 2.02 | n.s. (0.16) |
| Error | random | 0.6 | 44 | 0.01 | ||
| Total | 5.64 | 57 |
Figure 5B shows the constancy indices for both matte and glossy contextual spheres from Experiment 2, where the tests were 5 cd/m2. There was no significant effect of contextual sphere material, nor did contextual sphere material interact with the effect of test object or background (Table 3). The same interaction between matte disk and spheres is seen for the glossy contextual spheres as was observed for the matte contextual spheres. Note that the data for the matte contextual spheres in 5B are re-plotted from 5A and do not represent additional measurements.
Table 3. ANOVA for Experiment 2, 5 cd/m2 tests, both matte and glossy contextual spheres.
Observers were coded as a random variable. The main effect of each variable and the two-way interactions between all variables except observer were modeled. Data are for the 5 cd/m2 test luminance and both the matte and glossy contextual spheres. Note that the matte contextual sphere 5 cd/m2 data are the same as analyzed in Table 2.
| Source | VarType | SumSq | df | MeanSq | F | p |
|---|---|---|---|---|---|---|
| Observer | random | 0.08 | 4 | 0.02 | 2.71 | < 0.05 |
| Shape | fixed | 0.04 | 1 | 0.04 | 4.72 | < 0.05 |
| Context | fixed | 0 | 1 | 0 | 0 | n.s. (0.98) |
| Cue-Condition | fixed | 5.5 | 1 | 5.5 | 705.7 | < 0.001 |
| Shape*Context | fixed | 0 | 1 | 0 | 0 | n.s. (0.98) |
| Shape*Cue-Condition | fixed | 0.24 | 1 | 0.24 | 30.38 | < 0.001 |
| Context*Cue-Condition | fixed | 0 | 1 | 0 | 0.01 | n.s. (0.92) |
| Error | random | 0.38 | 49 | 0.01 | ||
| Total | 6.1 | 59 |
Discussion
We measured the color constancy of three-dimensional objects viewed in three-dimensional scenes, and compared this to constancy for a flat matte test embedded in the same scenes. We found that when we changed only the illuminant (consistent-cue conditions) constancy was very good for all of our test objects. In aggregate, however, constancy was slightly better for the flat matte disk than for the test spheres in the consistent-cue conditions (see Figures 4B, 5A, 5B; constancy better for disk except for 3 cd/m2 test luminance in 5A). Our consistent-cue conditions are similar to the manipulations studied in most experiments that assess constancy. In addition, we studied reduced-cue conditions. These silence local contrast as a cue to the illuminant change, and by studying them we separate the effect of local contrast from other processes that mediate constancy. As expected, constancy is much reduced in the reduced-cue conditions. Moreover, and most interesting, we found that constancy was systematically worse for the matte disk than for the test spheres (again Figures 4B, 5A, 5B). Although the effects of object shape are not huge, they are easily visible. To provide a sense for the interested reader the online supplement includes, for each observer for the 3 cd/m2 test conditions of Experiment 2, images that render the equivalent illuminant chromaticities for each object shape and cue condition. Our other manipulations (matte versus glossy sphere, matte versus glossy contextual spheres, test luminance) had little if any effect.
Our data present a fundamental challenge for generalizing theories of constancy developed for two-dimensional scenes to explain constancy for three-dimensional viewing. This challenge arises because there is no obvious intrinsic component of two-dimensional models that can explain an interaction between object shape and cue condition. Thus additional theory must be added before our current understanding of constancy for two-dimensional scenes can be applied to natural viewing. We return to this point below.
In Experiment 1, we found that constancy for a glossy test sphere was better than for a matte sphere, qualitatively consistent with earlier reports that adding specular highlights to a scene improves constancy (Yang & Maloney, 2001; Yang & Shevell, 2003). This effect did not replicate in Experiment 2, however. In addition, when we performed a manipulation more directly comparable to the earlier work by introducing glossy contextual spheres, we did not find improved constancy. We do not have an explanation for the difference in results between our current experiments and the earlier work.
There have been very few other studies of constancy for three-dimensional objects. Hedrich et al. (2009) used a memory-based paradigm and found that constancy with respect to spectral illumination changes for consistent-cue conditions was better for three-dimensional objects embedded in three-dimensional scenes than for two-dimensional objects embedded in two-dimensional scenes. De Almeida et al. (2010) carried out a similar comparison using a different experimental paradigm and reached a different conclusion: they found that constancy was similar across a switch between two-dimensional and three-dimensional viewing. Our data do not speak directly to the issues addressed by these papers, since in all of our conditions the test object was viewed in a three-dimensional scene. We do note that in our hands, the relative degree of constancy for two-dimensional versus three-dimensional tests depends on cue-conditions. There may be other cases where non-geometric aspects of the stimulus manipulations interact with the shape of the test, which could explain why different labs reach different conclusions.
Recent work from our lab examined constancy of perceived lightness and glossiness for three-dimensional objects rendered under spatially complex illumination fields (Olkkonen & Brainard, 2010; Olkkonen & Brainard, 2011). This work does not compare constancy for two- and three-dimensional objects, but does reveal striking interactions between object shape, illumination field, and perceived glossiness. While different in many details from the experiments presented here, these interactions have similar conceptual implications to those of the present results, namely that it may not be straightforward to use results obtained using one object shape to predict constancy for other object shapes.
An additional point of contact in the literature is that interactions similar to the ones we found have been observed when a flat test is moved in depth relative to a background; in that case consistent-cue constancy is best when the test is co-planar with the background, while the opposite was found for reduced-cue conditions (Werner, 2006; see also Radonjić, Todorović, & Gilchrist, 2010).
How might we think about the interaction between test object shape and the nature of the spectral changes in the contextual image? In natural scenes, the illuminant typically varies both with the position of an object in the scene and with the direction of the incident light (Debevec, 1998; Dror, Willsky, & Adelson, 2004; Koenderink, Pont, van Doorn, Kappers, & Todd, 2007). This means that that the light reflected from each location on an object depends on the three-dimensional orientation of the surface normal at that location, so that the visual processing required for constancy can vary across locations within a single object. Brainard and Maloney (2011) review a theory of how the visual system takes surface normal into account, based on studies of how the pose of matte planar surfaces affects their appearance (Boyaci, Maloney, & Hersh, 2003; Ripamonti et al., 2004; Bloj et al., 2004; Boyaci, Doerschner, & Maloney, 2004). Whether similar ideas can be applied to understand how individual locations within a single object are perceived is an open question, as is the question of whether it is fruitful to conceive of object color appearance as resulting from an integration of appearance computed at individual locations across the object’s surface (but see Xiao & Brainard, 2008; Olkkonen, Hansen, & Gegenfurtner, 2008; Ling, Vurro, & Hurlbert, 2008). Investigation of these questions strikes us as a promising direction to pursue as we seek to understand the interaction between shape and constancy.
A second important observation, developed most fully in the literature on lightness perception, is that the relative influence of different locations in a contextual image on the appearance of a test patch varies with the position and pose of that patch (Gilchrist et al., 1999; Adelson, 2000; Gilchrist, 2006). Given this, it may also be the case that variation in the shape of an object has a similar influence, and this could in turn produce an interaction between shape and constancy.
Supplementary Material
Acknowledgments
Supported by NIH RO1 EY10016 and P30 EY001583. We thank J. Andrews-Labenski, C. Broussard, & M. Suplick, for technical assistance. A. Radonjić provided helpful comments on the manuscript.
Footnotes
The supplemental material is available at http://color.psych.upenn.edu/supplements/constancy3Dobjects/.
References
- Adelson EH. Lightness perception and lightness illusions. In: Gazzaniga M, editor. The New Cognitive Neurosciences. 2nd ed MIT Press; Cambridge, MA: 2000. pp. 339–351. [Google Scholar]
- Allred SR, Brainard DH. Contrast, constancy, and measurements of perceived lightness under parametric manipulation of surface slant and surface reflectance. Journal of the Optical Society of America A. 2009;26(4):949–961. doi: 10.1364/josaa.26.000949. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arend LE, Reeves A. Simultaneous color constancy. Journal of the Optical Society of America A. 1986;3:1743–1751. doi: 10.1364/josaa.3.001743. [DOI] [PubMed] [Google Scholar]
- Blake A, Bülthoff H. Does the brain know the physics of specular reflection. Nature. 1990;343(6254):165–168. doi: 10.1038/343165a0. [DOI] [PubMed] [Google Scholar]
- Bloj M, Kersten D, Hurlbert AC. Perception of three-dimensional shape influences colour perception through mutual illumination. Nature. 1999;402:877–879. doi: 10.1038/47245. [DOI] [PubMed] [Google Scholar]
- Bloj M, Ripamonti C, Mitha K, Greenwald S, Hauck R, Brainard DH. An equivalent illuminant model for the effect of surface slant on perceived lightness. Journal of Vision. 2004;4:735–746. doi: 10.1167/4.9.6. [DOI] [PubMed] [Google Scholar]
- Boyaci H, Doerschner K, Maloney LT. Perceived surface color in binocularly viewed scenes with two light sources differing in chromaticity. Journal of Vision. 2004;4:664–679. doi: 10.1167/4.9.1. [DOI] [PubMed] [Google Scholar]
- Boyaci H, Maloney LT, Hersh S. The effect of perceived surface orientation on perceived surface albedo in binocularly viewed scenes. Journal of Vision. 2003;3:541–553. doi: 10.1167/3.8.2. http://journalofvision.org/3/8/2. [DOI] [PubMed] [Google Scholar]
- Brainard DH. Color constancy in the nearly natural image. 2. achromatic loci. Journal of the Optical Society of America A. 1998;15:307–325. doi: 10.1364/josaa.15.000307. [DOI] [PubMed] [Google Scholar]
- Brainard DH. Color constancy. In: Chalupa LM, Werner JS, editors. The Visual Neurosciences. MIT Press; Cambridge, MA: 2004. pp. 948–961. [Google Scholar]
- Brainard DH, Brunt WA, Speigle JM. Color constancy in the nearly natural image. 1. asymmetric matches. Journal of the Optical Society of America A. 1997;14:2091–2110. doi: 10.1364/josaa.14.002091. [DOI] [PubMed] [Google Scholar]
- Brainard DH, Longere P, Delahunt PB, Freeman WT, Kraft JM, Xiao B. Bayesian model of human color constancy. Journal of Vision. 2006;6:1267–1281. doi: 10.1167/6.11.10. http://journalofvision.org/6/11/10/ [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brainard DH, Maloney LT. Surface color perception and equivalent illumination models. Journal of Vision. 2011;11(5:1):1–18. doi: 10.1167/11.5.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brainard DH, Pelli DG, Robson T. Encyclopedia of Imaging Science and Technology. Wiley; 2002. Display characterization; pp. 72–188. [Google Scholar]
- Brainard DH, Wandell BA. Asymmetric color-matching: how color appearance depends on the illuminant. Journal of the Optical Society of America A. 1992;9(9):1433–1448. doi: 10.1364/josaa.9.001433. [DOI] [PubMed] [Google Scholar]
- Chichilnisky EJ, Wandell BA. Trichromatic opponent color classification. Vision Research. 1999;39:3444–3458. doi: 10.1016/s0042-6989(99)00033-4. [DOI] [PubMed] [Google Scholar]
- CIE . Colorimetry. third edition. Bureau Central de la CIE; Vienna: 2004. (No. 15.2004) [Google Scholar]
- CIE . Fundamental chromaticity diagram with physiological axes – Parts 1 and 2. Technical Report 170-1. Central Bureau of the Commission Internationale de l’ Éclairage; Vienna: 2007. [Google Scholar]
- de Almeida VMN, Fiadeiro PT, Nascimento SM. Effect of scene dimensionality on color constancy with real three-dimensional scenes and objects. Perception. 2010;39:770–779. doi: 10.1068/p6485. [DOI] [PubMed] [Google Scholar]
- Debevec P. Rendering synthetic objects into real scenes: bridging traditional and image-based graphics with global illumination and high dynamic range photography. Paper presented at SIGGRAPH; Orlando, FL. 1998. pp. 189–198. [Google Scholar]
- Delahunt PB, Brainard DH. Does human color constancy incorporate the statistical regularity of natural daylight? Journal of Vision. 2004;4(2):57–81. doi: 10.1167/4.2.1. http://www.journalofvision.org/4/2/1/ [DOI] [PubMed] [Google Scholar]
- Doerschner K, Boyaci H, Maloney LT. Human observers compensate for secondary illumination originating in nearby chromatic surfaces. Journal of Vision. 2004;4:92–105. doi: 10.1167/4.2.3. [DOI] [PubMed] [Google Scholar]
- Doerschner K, Boyaci H, Maloney LT. Testing limits on matte surface color perception in three-dimensional scenes with complex light fields. Vision Res. 2007;47(28):3409–3423. doi: 10.1016/j.visres.2007.09.020. http://www.ncbi.nlm.nih.gov/entrez/query.fcgi?cmd=Retrieve&db=PubMed&dopt=Citatio n&list_uids=18053846. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dror RO, Willsky AS, Adelson EH. Statistical characterization of real-world illumination. Journal of Vision. 2004;4:821–837. doi: 10.1167/4.9.11. [DOI] [PubMed] [Google Scholar]
- Fleming RW, Bülthoff HH. Low-level image cues in the perception of transluscent materials. ACM Transactions on Applied Perception. 2005;2:346–382. [Google Scholar]
- Fleming RW, Dror RO, Adelson EH. Real-world illumination and the perception of surface reflectance properties. Journal of Vision. 2003;3(5):347–368. doi: 10.1167/3.5.3. [DOI] [PubMed] [Google Scholar]
- Foster DH. Color constancy. Vision Research. 2011;51:674–700. doi: 10.1016/j.visres.2010.09.006. [DOI] [PubMed] [Google Scholar]
- Funt BV, Drew MS. Color constancy computation in near-Mondrian scenes using a finite dimensional linear model. Ann Arbor, MI: 1988. [Google Scholar]
- Gilchrist A. Seeing Black and White. Oxford University Press; Oxford: 2006. [Google Scholar]
- Gilchrist A, Kossyfidis C, Bonato F, Agostini T, Cataliotti J, Li X, Spehar B, Annan V, Economou E. An anchoring theory of lightness perception. Psychological Review. 1999;106:795–834. doi: 10.1037/0033-295x.106.4.795. [DOI] [PubMed] [Google Scholar]
- Gilchrist AL. Perceived lightness depends on perceived spatial arrangement. Science. 1977;195:185. doi: 10.1126/science.831266. [DOI] [PubMed] [Google Scholar]
- Gilchrist AL. When does perceived lightness depend on perceived spatial arrangement? Perception and Psychophysics. 1980;28:527–538. doi: 10.3758/bf03198821. [DOI] [PubMed] [Google Scholar]
- Granzier JJM, Brenner E, Cornelissen FW, Smeets JBJ. Luminance-color correlation is not used to estimate the color of the illumination. Journal of Vision. 2005;5(1):20–27. doi: 10.1167/5.1.2. [DOI] [PubMed] [Google Scholar]
- Griffin LD. Partitive mixing of images: A tool for investigating pictoria perception. Journal of the Optical Society of America A. 1999;16:2825–2835. [Google Scholar]
- Hedrich M, Bloj M, Ruppertsberg AI. Color constancy improves for real 3D objects. Journal of Vision. 2009;16(9:4):1–16. doi: 10.1167/9.4.16. [DOI] [PubMed] [Google Scholar]
- Helson H, Jeffers VB. Fundamental problems in color vision. II. Hue, lightness, and saturation of selective samples in chromatic illumination. Journal of Experimental Psychology. 1940;26:1–27. [Google Scholar]
- Helson H, Michels WC. The effect of chromatic adaptation on achromaticity. Journal of the Optical Society of America. 1948;38:1025–1032. doi: 10.1364/josa.38.001025. [DOI] [PubMed] [Google Scholar]
- Hochberg JE, Beck J. Apparent spatial arrangement and perceived brightness. Journal of Experimental Psychology. 1954;47:263–266. doi: 10.1037/h0056283. [DOI] [PubMed] [Google Scholar]
- Ishihara S. Tests for Colour-Blindness. Kanehara Shuppen Company, Ltd; Tokyo: 1977. [Google Scholar]
- Judd DB, MacAdam DL, Wyszecki GW. Spectral distribution of typical daylight as a function of correlated color temperature. Journal of the Optical Society of America. 1964;54:1031–1040. [Google Scholar]
- Kim J, Marlow P, Anderson BL. The perception of gloss depends on highlight congruence with surface shading. Journal of Vision. 2011;11(9:4) doi: 10.1167/11.9.4. [DOI] [PubMed] [Google Scholar]
- Koenderink JJ, Pont SC, van Doorn AJ, Kappers AM, Todd JT. The visual light field. Perception. 2007;36(11):1595–1610. doi: 10.1068/p5672. http://www.ncbi.nlm.nih.gov/entrez/query.fcgi?cmd=Retrieve&db=PubMed&dopt=Citatio n&list_uids=18265841. [DOI] [PubMed] [Google Scholar]
- Kraft JM, Brainard DH. Mechanisms of color constancy under nearly natural viewing. Proceedings of the National Academy of Sciences USA. 1999;96(1):307–312. doi: 10.1073/pnas.96.1.307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kraft JM, Maloney SI, Brainard DH. Surface-illuminant ambiguity and color constancy: effects of scene complexity and depth cues. Perception. 2002;31:247–263. doi: 10.1068/p08sp. [DOI] [PubMed] [Google Scholar]
- Lee HC. Method for computing the scene-illuminant chromaticity from specular highlights. Journal Of The Optical Society Of America A. 1986;3(10):1694–1699. doi: 10.1364/josaa.3.001694. [DOI] [PubMed] [Google Scholar]
- Ling Y, Vurro M, Hurlbert A. Surface chromaticity distributions of natural objects under changing illumination. Paper presented at 4th European Conference on Colour in Graphics, Imaging and Vision.2008. pp. 263–267. [Google Scholar]
- Marlow P, Kim J, Anderson BL. The role of brightness and orientation congurence in the perception of surface gloss. Journal of Vision. 2011;11(9:16) doi: 10.1167/11.9.16. [DOI] [PubMed] [Google Scholar]
- McCann JJ, McKee SP, Taylor TH. Quantitative studies in retinex theory: A comparison between theoretical predictions and observer responses to the ’Color Mondrian’ experiments. Vision Research. 1976;16:445–458. doi: 10.1016/0042-6989(76)90020-1. [DOI] [PubMed] [Google Scholar]
- Motoyoshi I, Nishida S, Sharan L, Adelson EH. Image statistics and the perception of surface qualities. Nature. 2007;447:206–209. doi: 10.1038/nature05724. [DOI] [PubMed] [Google Scholar]
- Newhall SM, Nickerson D, Judd DB. Final report of the O.S.A. subcommittee on the spacing of Munsell Colors. Journal of the Optical Society of America. 1943;33:385–412. [Google Scholar]
- Nickerson D. Spectrophotometric data for a collection of Munsell samples. U.S. Department of Agriculture; 1957. [Google Scholar]
- Nishida S, Shinya M. Use of image-based information in judgments of surface-reflectance properties. Journal of the Optical Society of America A. 1998;15(12):2951–2965. doi: 10.1364/josaa.15.002951. [DOI] [PubMed] [Google Scholar]
- Olkkonen M, Brainard DH. Perceived glossiness and lightness under real-world illumination. Journal of Vision. 2010;10(9:5) doi: 10.1167/10.9.5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olkkonen M, Brainard DH. Joint effects of illumination geometry and object shape in the perception of surface reflectance. i-Perception. 2011;2(9):1014–1034. doi: 10.1068/i0480. http://i-perception.perceptionweb.com/journal/I/volume/2/article/i0480. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olkkonen M, Hansen T, Gegenfurtner KR. Color appearance of familiar objects: effects of object shape, texture, and illumination changes. Journal of Vision. 2008;8(5):1–16. doi: 10.1167/8.5.13. [DOI] [PubMed] [Google Scholar]
- Olkkonen M, Hansen T, Gegenfurtner KR. Categorical color constancy for simulated surfaces. J Vis. 2009;9(12):1–18. doi: 10.1167/9.12.6. http://www.ncbi.nlm.nih.gov/entrez/query.fcgi?cmd=Retrieve&db=PubMed&dopt=Citatio n&list_uids=20053097. [DOI] [PubMed] [Google Scholar]
- Pessoa L, Mingolla E, Arend LE. The perception of lightness in 3-D curved objects. Perception & Psychophysics. 1996;58(8):1293–1305. doi: 10.3758/bf03207560. [DOI] [PubMed] [Google Scholar]
- Radonjić A, Todorović D, Gilchrist A. Adjacency and surroundedness in the depth effect on lightness. Journal of Vision. 2010;10(9:12):1–16. doi: 10.1167/10.9.12. [DOI] [PubMed] [Google Scholar]
- Ripamonti C, Bloj M, Hauck R, Mitha K, Greenwald S, Maloney SI, Brainard DH. Measurements of the effect of surface slant on perceived lightness. Journal of Vision. 2004;4:747–763. doi: 10.1167/4.9.7. http://journalofvision.org/4/9/7. [DOI] [PubMed] [Google Scholar]
- Sharon L, Li Y, Motoyoshi I, Nishida S, Adelson EH. Image statistics for surface reflectance perception. Journal of the Optical Society of America A. 2008;25:846–865. doi: 10.1364/josaa.25.000846. [DOI] [PubMed] [Google Scholar]
- Stockman A, Sharpe LT. Spectral sensitivities of the middle- and long-wavelength sensitive cones derived from measurements in observers of known genotype. Vision Research. 2000;40:1711–1737. doi: 10.1016/s0042-6989(00)00021-3. [DOI] [PubMed] [Google Scholar]
- Todd JT, Norman JF, Mingolla E. Lightness constancy in the presence of specular highlights. Psychological Science. 2004;15:33–39. doi: 10.1111/j.0963-7214.2004.01501006.x. [DOI] [PubMed] [Google Scholar]
- Tominaga S, Wandell BA. The standard surface reflectance model and illuminant estimation. Journal of the Optical Society of America A. 1989;6(4):576–584. [Google Scholar]
- Vos JJ. Colorimetric and photometric properties of a 2 degree fundamental observer. Color Research and Application. 1978;3:125–128. [Google Scholar]
- Ward GJ. Measuring and modeling anisotropic reflection. Paper presented at SIGGRAPH ’92: Proceedings of the 19th annual conference on computer graphics and interactive techniques.1992. pp. 265–272. [Google Scholar]
- Ward GJ. The RADIANCE lighting simulation and rendering system. Paper presented at Proceedings of ACM SIGGRAPH; July 24-29, 1994.1994. pp. 459–472. [Google Scholar]
- Werner A. The influence of depth segregation on colour constancy. Perception. 2006;35:1171–1184. doi: 10.1068/p5476. [DOI] [PubMed] [Google Scholar]
- Xiao B, Brainard DH. Surface gloss and color perception of 3D objects. Visual Neuroscience. 2008;25:371–385. doi: 10.1017/S0952523808080267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang JN, Maloney LT. Illuminant cues in surface color perception: tests of three candidate cues. Vision Research. 2001;41:2581–2600. doi: 10.1016/s0042-6989(01)00143-2. [DOI] [PubMed] [Google Scholar]
- Yang JN, Shevell SK. Surface color perception under two illuminants: the second illuminant reduces color constancy. Journal of Vision. 2003;3:369–379. doi: 10.1167/3.5.4. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.