Temperature dependence of fast carbonyl backbone dynamics in chicken villin headpiece subdomain

Abstract

Temperature-dependence of protein dynamics can provide information on details of the free energy landscape by probing the characteristics of the potential responsible for the fluctuations. We have investigated the temperature-dependence of picosecond to nanosecond backbone dynamics at carbonyl carbon sites in chicken villin headpiece subdomain protein using a combination of three NMR relaxation rates: ¹³C′ longitudinal rate, and two cross-correlated rates involving dipolar and chemical shift anisotropy (CSA) relaxation mechanisms, 13C′/¹³C′−¹³C^α CSA/dipolar and 13C′/¹³C′−¹⁵N CSA/dipolar. Order parameters have been extracted using the Lipari-Szabo model-free approach assuming a separation of the time scales of internal and molecular motions in the 2–16°C temperature range. There is a gradual deviation from this assumption from lower to higher temperatures, such that above 16°C the separation of the time scales is inconsistent with the experimental data and, thus, the Lipari-Szabo formalism can not be applied. While there are variations among the residues, on the average the order parameters indicate a markedly steeper temperature dependence at backbone carbonyl carbons compared to that probed at amide nitrogens in an earlier study. This strongly advocates for probing sites other than amide nitrogen for accurate characterization of the potential and other thermodynamics characteristics of protein backbone.

Introduction

Temperature-dependence of protein dynamics can provide information on the details of the free energy landscape by probing the characteristics of the potential responsible for the fluctuations. (Cavanagh and Akke 2000; Wand 2001) This, in turn, provides means of determining various thermodynamics parameters such as configurational entropy and heat capacity, which play an important role in ligand-binding (Bracken et al. 1999), protein–protein interactions, and protein stability(Jaenicke 2000; Schuler et al. 2002). NMR has an advantage of probing selective contributions from various parts of the protein depending on chosen isotopical labeling patterns and pulse sequences employed. Most of temperature-dependent NMR studies of backbone dynamics at picosecond-to-nanosecond time scale have been performed on amide nitrogens (Mandel et al. 1996; Yang et al. 1997; Seewald et al. 2000; Spyracopoulos et al. 2001; Vugmeyster et al. 2002; Idiyatullin et al. 2003; Massi and Palmer 2003; Krizova et al. 2004; Johnson et al. 2007).

NMR relaxation studies focused on amide nitrogen nuclei primarily probe fast picosecond motions of the N–H bond vector. However, they miss on other modes of motions of the peptide plane, particularly those that occur around an imaginary axis which is parallel to the N–H bond vector. (Wang et al. 2003b) Carbon nuclei at backbone carbonyl sites provide complimentary probes in this regard as they report on a different subset of motions, which is supported by studies on several proteins such as ubiquitin, ribonuclease binase, calmodulin, ribonuclease T1, and dematin headpiece C-terminal domain (Engelke and Ruterjans 1997; Pang et al. 2002; Wang et al. 2003b, 2005, 2006; Chang and Tjandra 2005; Vugmeyster et al. 2010) This implies a different local potential governing fast fluctuations of the N–H bond vectors versus the fluctuations of other atoms of peptide planes and reinforces the need for temperature-dependence studies at nuclei other than nitrogen in order to fully characterize the thermodynamic contribution of protein backbone to configurational entropy and heat capacity. The results of the study by Wang et al. (2003b) on ubiquitin and binase using ¹³C′/¹³C′−¹³C^α cross-correlated rate measurements indicated a remarkably strong temperature dependence of the carbonyl dynamics compared to dynamics at amide nitrogen sites. It is important to investigate whether these conclusions are applicable to other proteins and are supported by more refined methodologies.

To extract dynamical information from the NMR relaxation rates one needs a theoretical framework which relates the experimental rates to motional parameters. The most popular analysis of solution NMR relaxation studies is based on the model-free formalism of Lipari and Szabo and its extension by Clore et al. (Lipari and Szabo 1982; Clore et al. 1990) This treatment does not employ a specific model of motions and assumes an independence of internal fluctuations and overall tumbling of a molecule. This methodology has yielded many invaluable results and, importantly, has been applied to a large variety of proteins. As a result it allows for comparison among many different proteins and facilitates investigations of general principles governing backbone dynamics. The popularity of the approach is supported by its simplicity and the availability of standard pulse sequences for the measurements of laboratory frame relaxation rates at amide sites and computational tools for data analysis (Farrow et al. 1994; Orekhov et al. 1994; Mandel et al. 1995; Cole and Loria 2003). Limits of the validity of the model-free formalism, as well as alternative treatments and discussions have been recently presented (Vugmeyster et al. 2003; Frederick et al. 2008; Halle 2009; Meirovitch et al. 2009, 2010).

In this work we will investigate the temperature dependence of backbone dynamics at carbonyl sites in chicken villin headpiece subdomain(HP36). HP36 is a 36-amino acid helical thermostable protein that has been a subject of numerous experimental and theoretical studies due to its small size and fast folding rate (McKnight et al. 1996; Vugmeyster et al. 2002; Wang et al. 2003a; Brewer et al. 2005; Havlin and Tycko 2005; Kubelka et al. 2006; Tang et al. 2006; Wickstrom et al. 2006, 2007; Thurber and Tycko 2008; Vugmeyster and McKnight 2008; Vugmeyster et al. 2009; Xiao et al. 2009) Experimental temperature-dependence of the dynamics at amide nitrogen sites has been measured in an earlier study (Vugmeyster et al. 2002) and in the work by Massi and Palmer (2003) molecular dynamics simulations were used to obtain the temperature-dependent potential of mean force.

We will employ the experimental methodology similar to the one developed by Wang et al. (2006), which is based on the measurement of three relaxation rates: ¹³C′ longitudinal NMR relaxation rate R₁ and two cross-correlated rates involving dipolar and chemical shift anisotropy (CSA) relaxation mechanisms, ¹³C′/¹³C′−¹³C^a CSA/dipolar and ¹³C′/¹³C′−¹⁵N CSA/dipolar, denoted by R_{C′/C′−Cα} and R_{C′/C′−N}, respectively. All three ¹³C′ relaxation rates are least sensitive to rotational fluctuations about an imaginary C^α–C^α axis, a so-called crank-shaft motions(Bremi and Bruschweiler 1997), and most sensitive to rotational fluctuations about an imaginary axis parallel to the N–H bond direction, a so-called α-axis. This methodology is superior to the measurements based on the R_{C′/C′−Cα} rates only, in particular because the order parameters extracted from this approach do not rely on the assumption of infinitely fast internal motions.

Our analysis will assume the separation of time scales of internal motions and overall tumbling and will demonstrate a remarkably stronger temperature-dependence of fast carbonyl dynamics compared to the one probed at the backbone nitrogen sites. We will also sho that our data provide an interesting example on the similarity of the time scales of the overall and internal motions for HP36 protein at temperature above ~16°C and, thus, illustrates the limit of the applicability of the Lipari-Szabo approach for the analysis of NMR relaxation rates.

Materials and methods

Sample preparation

¹⁵N/¹³C labeled chicken villin headpiece subdomain sample was prepared according to the procedure described in Bi et al. (2006) The essence of the procedure consists of linking HP36 via a factor Xa cleavage sequence to the C-terminus of the N-terminal domain of the ribosomal protein L9. The following modifications were used: the protein was expressed in minimal media with 0.8 g/l ¹⁵N NH₄Cl and 3 g/l ¹³C-glucose. A G50 column (size 2 cm × 100 cm) with 20 mM Tris, 100 mM NaCl, 5 mM CaCl₂, and 0.01% azide buffer at pH 7.5 was used for a first purification step, followed by a cleavage by factor Xa. The cleavage was performed at room temperature with 8 units of factor Xa per mg of protein. The product was lyophilized and purified by Reverse-Phase HPLC. The identity and purity of the sample was confirmed by mass spectroscopy, N-terminal sequencing, ¹⁵N NMR HSQC, and Reverse-Phase HPLC.

The protein was dissolved in 350 μl of 90% H₂O/10% D₂O to a concentration of 1.4 mM with 50 mM sodium acetate-D₃ buffer and the pH was adjusted to 5.4. A Shigemi tube made of susceptibility-matched glass was used.

NMR spectroscopy

As mentioned in the introduction, the strategy of Wang et al. (2006) used in our studies is based on the measurement of three relaxation rates: ¹³C′R₁, R_{C′/C′−Cα} and R_{C′/C′−N}. All data were acquired on a 500 MHz Bruker NMR spectrometer equipped with triple resonance triple-gradient TXI probe. The measurement were taken at five temperatures, 2, 6, 12, 16, and 22°C with the temperature calibration performed using a deuterated methanol sample (Findeisen et al. 2007). For all three rates 512 × 40 complex points were acquired with the spectral width of 12 and 25 ppm in ¹H and ¹⁵N dimensions, respectively. Recycle delay of 1.5 s was used. The data were processed by the NmrPipe/NmrDraw/NlinLS package (Delaglio et al. 1995). Each dimension was apodized by a 90° phase-shifted sine-bell window function and zero-filled once.

¹³C′ R₁ longitudinal relaxation rates were measured by a two-dimensional HN(CO) type pulse sequence(Kay et al. 1990) taking care to suppress cross-correlated mechanisms involving N, H, and C^α nuclei with 180° pulses. Data with six relaxation delays between 0.01 and 1.4 s were recorded. The number of scans used was 24. The relaxation rates were obtained by fitting signal intensities to a mono-exponential decay. The uncertainties in rates were obtained by jack-knife simulations (Mosteller and Tukey 1977). R_{C′/C′−Cα} and R_{C′/C′−N} cross-correlated rates were measured using HN(CO) type pulse sequences described in Loth et al. (2005). The experiments are based on the principle of symmetrical reconversions (Pelupessy et al. 2003, 2007), which results in a more accurate measurements of cross-correlated relaxation rates than earlier techniques. Cross-correlation causes inter-conversions between two operators, in general denoted by P and Q. They are given by $C_y^{\prime }$ and $2C_y^{\prime }{C}_z^{\alpha }$ operators for the R_{C′/C′−Cα} experiment and $C_y^{\prime }$ and $2C_y^{\prime }$ N_z operators for the R_{C′/C′−N} experiment. Four measurements, denoted by I, II, III, and IV, are acquired in order to determine each cross-correlated rate. Experiment I measures the decay of P, IV the decay of Q, II the conversion P → Q, and III the conversion Q → P. The cross-correlated rate is extracted from the peak volumes of the four interleaved experiments as $\mid R\mid =\frac{1}{T}{\text{tanh}}^{-1}\sqrt{\frac{A_{II}{A}_{III}}{A_I{A}_{IV}}}$, where T is the relaxation delay time. The sign of the rate is determined by comparing the sign of intensities in the four experiments. The errors in the cross-correlated rates were estimated by assuming that errors in the intensity for each experiment are given by noise level in corresponding spectra. Data with the relaxation delay of 80 ms were acquired at all temperatures. An additional R_{C′/C′−N} data set with the relaxation delay of 60 ms was collected for 22°C. 32 scans were used for experiments I and IV, and either 64 (R_{C′/C′−Cα}) or 128 (R_{C′/C′−N}) for experiments II and III.

The following residues had inherently lower intensities and, as a result, a reliable value for at least one of the cross-correlated rates could not be obtained at all temperatures: D44, D46, G52, M53, N60.

Determination of 13C′ order parameters

The experimental rates are fitted to corresponding spectral densities expressions to obtain effective ¹³C′ order parameters, local correlation times and directions of ¹³C′ CSA tensors. The expressions for the rates in terms of the spectral densities are given in references (Goldman 1984; Boyd et al. 1991; Brutscher et al. 1998; Fischer et al. 1998; Wang et al. 2006).

To parameterize the experimental rates we used the following model-free spectral density expression which assumes identical order parameters S² for all pairs of interactions a and b (Wang et al. 2006):

$$J^{ab}=\frac{2}{5}\left(\frac{S^2{\tau }_c}{1+{\left(\omega {\tau }_c\right)}^2}+\frac{(1-S^2)\tau }{1+{\left(\omega \tau \right)}^2}\right)P_2\left(\text{cos}{\theta }^{ab}\right).$$ (1)

For auto-correlated terms a = b. P₂ is the second order Legendre polynomial and θ^ab is the angle between chosen components of the two interactions.$\tau =\frac{{\tau }_c{\tau }_e}{{\tau }_c+{\tau }_e}$,, where τ^e reflects an average of local motions affecting a and b simultaneously. The interaction angles relevant to R_C′/_C′−Cα differ from angles relevant to the R_C′/_C′−N by the C^α−C′−N bond angle of 117°. Note that S² is related to the standard notation of the cross-correlated order parameter as S^ab = S²P₂(cosθ^ab).

In addition to the relaxation rates, a list of isotropic ¹³C′ chemical shifts is required in order to estimate the components of carbonyl CSA tensor using the rules described in Loth et al. (Loth et al. 2005). It is also necessary to have the values of the overall tumbling time.

¹³C′ assignments necessary for chemical shift estimates were previously obtained at 20°C (Vugmeyster and McKnight 2008). We have repeated the assignments at 8°C. The 8°C assignments were used for 2, 6, and 12°C temperatures, whereas the 20°C assignments were used for 16 and 22°C temperatures.

The values of S², τ_e, θ and h, the angle representing the orientation of σ₁₁ axis (least shielded component) of ¹³C′ CSA tensor with respect to C′−C^α bond were obtained by a constrained (bounded) minimization of x² function in Matlab. Boundaries for the fitting parameters were as follows: 0 < S² < 1, τ_c/1,000 < τ_e < τ_e,max, 100° < θ < 200°. τ_e,max, was selected as τ_c/2 to obtain the main results of the paper, but varied for checks and validations. The standard Matlab routine for bounded minimization fminbnd only allows for a one-dimensional minimization (Brent 1973; Forsythe et al. 1976). For several dimensions the specific order of minimizations has to be chosen. We have used the following sequence: min_τe min_S² min_θ x² (τ_e,S²,θ). In practice, the specific order did not matter. Several other orderings led to results coinciding with the initial one within the accuracy of the algorithm. For practical purposes, actual minimization was done over ln(τ_e). The possibility of another minimum of x² was ruled out by inspection of x²(τ_e) with fixed values of τ_e while minimizing with respect to S² and θ. This choice was made based on the observation of Wang et al. (2006) that when there are two minima their positions vary substantially in τ_e values. A second minimum in x²(τ_e) was not observed for any residue.

The validity of the fitting procedure was confirmed by constructing synthetic data sets of rates from a range of S², τ_e, and τ_c values using the spectral density of the form specified by Eq. 1 and confirming that the algorithm returns the original values of these parameters. The parameters were taken as S² = 0.95, 0.9, 0.8, 0.7; τ_e = τ_c/2, τ_c/3, τ_c/5, τ_c/10, τ_c/50 for τ_c of either 3 or 5 ns; C_iso = 175 ppm and θ = 155°. “Experimental errors” were specified as 3, 5, and 7% of the average values to the synthetic R₁, R_C′/_C′−Cα and R_C′/_C′−N, respectively; these percentages are close to the average of actual experimental errors. x² minimization led to the exact reproduction of initial S² values with simulated errors in 0.03–0.05 range.

The following residues had to be excluded due to large x² values: K65 at 2°C, F47 and V50 at 6°C, and A59, K73 at 16°C. In addition, residues with data available for less than three temperature points were excluded from the analysis of the temperature dependence. A total of 26 residues were used in the analysis.

Results and discussion

Temperature dependence of carbonyl order parameters is much stronger compared to its backbone nitrogen counterpart.

Generalized order parameters at amide nitrogen sites have been previously obtained in the range of temperatures between 2 and 32°C for HP36 (Vugmeyster et al. 2002), at which the protein is at least 99% folded (McKnight et al. 1996). HP36 has been previously shown to tumble isotropically and the molecular tumbling times were determined on a ¹⁵N labeled sample. The latter were shown to be consistent with the Stokes-Einstein relationship if 1.5 layers of hydration is included. Thus, we can use this approach to adjust the molecular tumbling times for the ¹³C/¹⁵N sample, which yields the values of 4.97, 4.36, 3.64, 3.11, and 2.65 ns for 2, 6, 12, 16, and 22°C, respectively.

Our initial goal was to investigate backbone carbonyl dynamics over the whole 2–32°C range, however, due to the small tumbling times the values of the smallest relaxation rate, R_C′/_C′−N, could not be measured reliably above about 22°C. In addition, as will be shown and discussed in detail in the next section, the separation of time scales of the overall and internal motions, and, thus, the validity of the Lipari-Szabo approach could not be assumed for the data at 22°C. We have therefore obtained the order parameters at four temperatures, 2, 6, 12, and 16°C.

As elaborated in Materials and Methods Section, the values of effective order parameters S² at carbonyl sites, as well as internal correlation times τ_e and the angles θ representing the orientation of σ₁₁ axis (least shielded component) of ¹³C′ CSA tensor with respect to C′−C^α bond vector are obtained by fitting three experimental relaxation rates to the spectral density of the form of Eq. 1, according to the approach developed by Zuiderweg and coworkers (Wang et al. 2006). The amplitude of local fluctuations for all interactions contributing to the three experimental rates at each site is assumed to be the same, and is thus reflected in a single effective value of the ¹³C′ order parameter. The fits were constrained by τ_e < τ_c=2 under the assumption of the separation of the time scale of the molecular and internal motions. This constraint is somewhat arbitrary and its significance will be discussed in the following section.

The values of effective order parameters obtained from the experimental rates are shown in Fig. 1 for 2, 6, 12, and 16°C. A much stronger temperature dependence is observed compared to the amide nitrogen data. The average difference in carbonyl order parameters between 2 and 16°C is 0.18 ± 0.05, while it is 0.029 ± 0.015 for the nitrogen order parameters in the same temperature range.

Fig. 1.

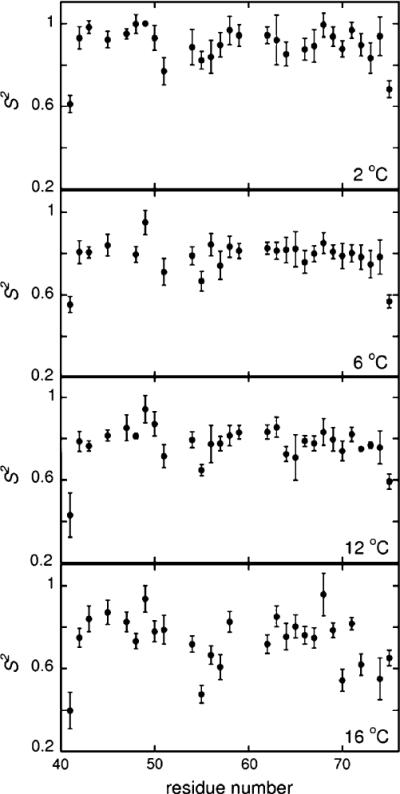
Plots of order parameters versus residue number. The numbering of residues in HP36 starts with #41

To quantify the temperature dependence of order parameters we look at the slopes of plots of 1-S versus T. The meaning of the slope is easiest to see if we consider motions which are restricted to small excursions within an axially symmetric parabolic potential. In this case (Mandel et al. 1996), $\frac{d(1-S)}{dT}=\frac{3}{2}\frac{d<{\alpha }^2>}{dT}$, where α is the fluctuating angle. For other types of potentials the slopes 1 - S versus T provide a measure of temperature dependence in a selected temperature interval. The results are presented in Fig. 2 and Table 1. The resulting weighted average value is 4.9 × 10⁻³ ± 2 × 10⁻⁴ 1/K, which is over 2.5 times larger than the value obtained from the backbone nitrogen data, 1.81 × 10⁻³ ± 6 × 10⁻⁵ 1/K. Note that there are substantial variations among the residues (see SI5 for 1 - S versus T plots for all amino acids) and for six residues, F51, A59, L63, K65, N68, and L75 the temperature-dependence is not discernible within the error limits. The quality of the data is not sufficient to judge whether this is due to actual physical differences or insufficient precision.

Fig. 2.

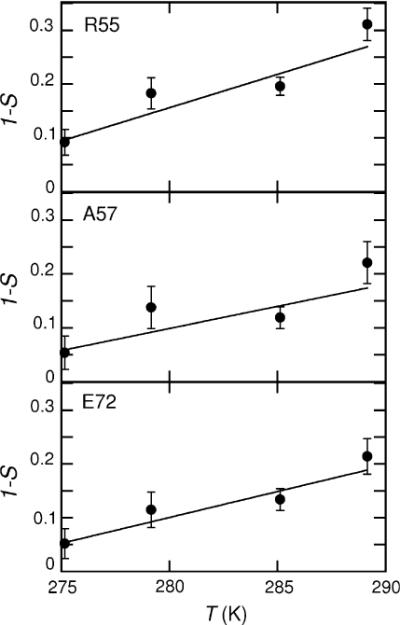
Sample plots of 1 – S versus T

Table 1.

The values of slopes of 1-S versus T plots

Residue	Slope (1/K) × 103	Residue	Slope (1/K) × 103
41	11.1 ± 1.0	62	6.6 ± 3.0
42	6.4 ± 1.9	63	−1.6 ± 1.8
43	8.3 ± 4.7	64	6.1 ± 1.9
45	3.7 ± 2.4	65	0.7 ± 5.1
47	4.8 ± 0.2	66	3.4 ± 2.2
48	7.2 ± 3.7	67	4.1 ± 1.5
49	2.7 ± 0.7	68	3.8 ± 5.0
50	5.5 ± 2.0	69	4.5 ± 2.6
51	−0.3 ± 2.6	70	11.7 ± 3.1
54	4.7 ± 2.2	71	4.8 ± 3.0
55	12.3 ± 3.9	72	8.3 ± 2.8
56	8.4 ± 1.9	73	2.9 ± 2.2
57	8.3 ± 4.4	74	12.8 ± 4.1
58	4.2 ± 2.7	75	0.5 ± 3.9
59	4.2 ± 5.3

Our results support the conclusion reached by Zuiderweg and coworkers (Wang et al. 2003b) regarding the temperature-dependence of carbonyl backbone motions in ubiquitin and binase on the basis of R_{C′/C′−Cα} rates measurements. A substantially larger temperature dependence of backbone carbonyl order parameters indicates the necessity of probing multiple nuclei of the peptide plane in order to calculate the potential and other thermodynamic characteristics of protein backbone.

The deviation from the decoupling approximation gradually increases and the assumption of time scale separation is not valid for the rates above ~16°C.

The commonly used Lipari-Szabo model (1982) for the analysis of relaxation data in macromolecules and its extension by Clore and coworkers (1990) represent a macroscopic phenomenological approach in which the correlation function describing NMR relaxation is parameterized by model-independent parameters, such as order parameters describing the amplitudes of motions and correlation times describing the time scales of motions. This approach uses a well-known decoupling approximation in which molecular and internal motions give independent contributions into the correlation function. The decoupling assumption is likely to break down when the ratio of correlation times for internal and overall motions, τ_e/τ_c; is not considerably smaller than 1. Several approaches have been developed that take into account correlations between the overall and internal motions (Meirovitch et al. 2009) and it has been shown that the Lipari-Szabo approach overestimates the values of the order parameters. This result has been obtained in a microscopic Slowly Relaxing Local Structure model by Tugarinov and coworkers (2001), as well as in a macroscopic phenomenological description by Vugmeyster et al. (2003) The latter approach estimates the upper limit of the correction to the order parameters is given by the factor of τ_c/(τ_c – τ_e); note, that this approach still requires a separation of the time scales of the overall and internal motions.

Correlation times at backbone nitrogen sites are usually short, as a result in order to see the deviations from the Lipari-Szabo assumption a sophisticated analysis of the data would be necessary. In contrast, as have been seen in a number of works, internal correlation times at backbone carbonyl sites tend to be much longer, on the order of 500–1,000 ps or larger, and thus the deviations for the decoupling assumption should be more significant. If the size of the protein under consideration is about 5 kDa, the separation of the time scales of the molecular and internal motions can approach the limit at which the model-free approach is not valid.

The small size of HP36 with the correlation time for overall tumbling of about 2.7 ns at 22°C makes it a good candidate for a direct observation of the limit of applicability of the decoupling approximation. As we will show below, the separation of the time scales is no longer valid for carbonyl motions at temperatures above 16°C.

The most straightforward assessment of the separation of the time scales would be based on reliable values of τ_e. Yet for the majority of the residues the fit of the relaxation rates to the spectral densities of Eq. 1 have not yielded reliable τ_e values, as indicated by very large uncertainties and the values falling on the upper boundary given by τ_c/2. For lower temperatures this is likely due to the fact that for most residues the values of the order parameters are close to unity, and thus the fits to Eq. 1 are not sensitive to the values of τ_e. For higher temperatures, this is due to the fact that the fits can not fix the value of τ_e for a large ratio of τ_e/τ_c. To analyze this issue in detail we have generated a synthetic data set for the τ_c value of 3.65 ns, corresponding to the tumbling time of HP36 at 12°C, S² values in the range of 0.6–0.9, and with τ_e varied from 0.1 to 0.5 multiples of τ_c. The synthetic data were then re-fitted to Eq. 1. The results indicate that no reliable values can be expected for τ_e values when the ratio τ_e/τ_c reaches a certain threshold: τ_e/τ_c<0:3 for S² = 0.6, τ_e/τ_c < 0:2 for S² = 0.8, and τ_e/τ_c < 0:1 for S² = 0.9. However, the values of the order parameters can be determined with a reasonable accuracy even for large τ_e/τ_c ratios. The analysis, presented in detail in Supporting Information SI1, suggests that for the majority of residues at temperatures above 6°C the values of τ_e are larger than 0.2τ_c.

We think that the fact that the time scale of carbonyl motions is so much longer than that of N–H vectors for the whole temperature range points to the conclusion that the motions of the N–H bond vectors are dominated by fast proton fluctuations, either inside or outside the peptide plane, in which the rest of the nuclei of the peptide plane are not involved. In contrast, the motions of the carbonyl carbons contributing to the relaxation rates are likely to coincide with the motion of the peptide plane as a whole.

We have done the following check to further assess the stability of the fitted order parameters and the validity of the assumption of the separation of the time scales: we looked at the changes in S² values when the upper boundary constraining the allowable values of τ_e was varied from τ_c/3 to τ_c/2, as well as at the changes in corresponding χ² values. There is a trend from the lower to upper temperatures to make S² values more and more sensitive to the chosen τ_e upper boundary (first row of Table 2). Though χ² values are acceptable for all temperatures for τ_e <τ_c/2 boundary (second row of Table 2), they rise more sharply for higher temperatures when the boundary is lowered (third row of Table 2). This suggests that τ_e is approaching τ_c/2 and the decoupling approximation becomes questionable. This trend also implies that the temperature dependence of τ_e is much less than that of τ_c. At 22°C the molecular tumbling time is 2.7 ns and the τ_e/τ_c ratio must be large enough to render the correlation function sensitive to the details of molecular motion and, thus, the Lipari-Szabo approach can no longer be applied.

Table 2.

Analysis of the sensitivity of the fits to τ_e boundary

	2°C	6°C	12°C	16°C	22°C
Average (|S2 (τc/2) – S2 (τc/3)|)	0.0038	0.0036	0.011	0.022	0.060
Median χ2 (τc/2)	0.98	0.058	0.54	1.1	1.8
Median (χ2 (τc/3) – χ2 (τc/2))	0.020	0.15	1.2	3.8	10

The values in brackets represent the upper limit of constraints imposed on the values of τ_e in the fitting procedure

We note that the values of θ are robust to variations in τ_e boundary. Fitted values of θ (SI3) do not differ across 2–16°C temperature range within the experimental errors, as expected for the folded state. Also the changes in the values of the order parameters are negligible if the angles θ are fixed as the average values reported in Table SI3. This is in part due to the fact that the rates R₁ do not depend on θ and, being the rates with the smallest experimental errors, they impose the most stringent constraints on the values of S² and τ_e.

One could argue that there are a number of assumptions inherent in Eq. 1, the most prominent being the assumption of the same order parameters for all interactions contributing to the carbonyl relaxation rates, which, in turn, implies isotropic local motions. Due to the fact that this approach has worked relatively well for several other proteins (Wang et al. 2006; Vugmeyster et al. 2010) at room temperature with similar amplitudes of fast motions to the ones seen for HP36 at 16°C, it is unlikely that the assumption plays an important role in the temperature-dependent trend that we observe.

Importantly, the correction to the decoupling approximation, discussed above, would make the temperature dependence of the carbonyl order parameters in the 2–16°C temperature range even larger, as the values of the order parameters are expected to be overestimated by a larger extent at higher temperatures. Even though we can not calculate these corrections quantitatively due to large uncertainties in the values of τ_e, the corrections would increase the values of the slopes of 1 – S versus T slopes, thus strengthening the main conclusion regarding the temperature dependence of the carbonyl dynamics.

One of the alternative approaches to the analysis of the experimental rates would be not to constraint the fits to Eq. 1 by the condition τ_e<τ_c/2: This would allow for a wider range of possibilities for both the order parameters and internal correlation times. Figure 3 displays a representative plot showing a range of allowable values of the order parameters and internal correlation times without any constraint on τ_e. We observe that for large values of τ_e there is a range of values of the order parameters and correlation times that fit the experimental data, which is consistent with a general behavior of the Lipari-Szabo type spectral densities. While this approach may yield statistically better fits, the meaning of the fitted parameters will not be the same as in the conventional model-free approach and its interpretation will require a consideration of a coupling between the internal and the overall motions. We, therefore, decided to constraint our analysis with the assumption of the separation of the time scales for the overall and molecular motions.

Fig. 3.

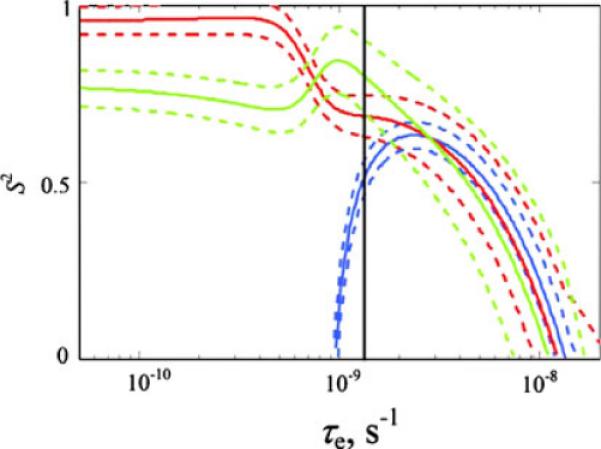
A representative plot showing the range of S² and τ_e values consistent with the experimental rates. The data are shown for T54 at 22°C. Solid lines represent S² and τ_e values that fit R₁ (blue), R_{C′/C′-Cα} (green) and R_C′/C′-N (red) relaxation rates. Dotted lines mark the area of the parameters that fit the rates within the limits of the experimental errors. The black vertical line represents the boundary τ_e = τ_c2: The angle θ was fixed by the following procedure: for each value of τ_e, the χ² function was minimized with the respect to S² and θ. The resulting value of θ was then used to calculate S² which reproduces the experimental values of R_{C′/C′-Cα} and R_C′/C′-N rates for a given τ_e

Conclusion

We have looked at the temperature dependence of the order parameters of fast motions at carbonyl carbon backbone sites in HP36 protein and compared it to an earlier study of amide nitrogen order parameters. The order parameters were obtained in 2−16°C temperature range using the model-free spectral density and assuming (a) that the amplitudes of local fluctuations for all interactions contributing to the three experimental rates are the same and (b) the separation of the time scales of molecular and internal motions, reflected in imposing the constraint on the fitting procedure as τ_e<sτ_c/2

While there are variations among the residues, on the average the carbonyl sites show a markedly steeper temperature dependence. The values of slopes in 1 – S versus T plots are on the average ~2.5 larger compared to the values obtained for the nitrogen sites. The results emphasize the need to probe nuclei other than nitrogen for accurate determination of the protein backbone potential and thermodynamic characteristics.

The small size of HP36 protein coupled to relatively long and weakly temperature-dependent values of internal correlation times led to an observation of the limit of the applicability of the decoupling approximation in the Lipari-Szabo model-free approach. As the temperature is raised and the molecular tumbling time decreases, the analysis of the data indicates a gradual deviation from the decoupling approximation. Above ~16°C the separation of time scales can no longer be assumed, at which point the model-free formalism can not be applied. While the importance of the separation of the time scales for the Lipari-Szabo approach has been discussed in a number of works, to our knowledge this work is the first to present the experimental evidence that the separation can fail for fast motions of the backbone.