Analytical Tools To Distinguish the Effects of Localization Error, Confinement, and Medium Elasticity on the Velocity Autocorrelation Function

Abstract

Single particle tracking is a powerful technique for investigating the dynamic behavior of biological molecules. However, many of the analytical tools are prone to generate results that can lead to mistaken interpretations of the underlying transport process. Here, we explore the effects of localization error and confinement on the velocity autocorrelation function, C_υ. We show that calculation of C_υ across a range of discretizations can distinguish the effects of localization error, confinement, and medium elasticity. Thus, under certain regimes, C_υ can be used as a diagnostic tool to identify the underlying mechanism of anomalous diffusion. Finally, we apply our analysis to experimental data sets of chromosomal loci and RNA-protein particles in Escherichia coli.

Introduction

The cytoplasm is a crowded and heterogeneous medium (1). To understand how this complex and dynamic environment affects biological processes, single particle tracking (SPT) can be used to characterize the motion of molecules inside the cell (2,3). In a typical experiment, the position $\overrightarrow{R}\left(t\right)$ of a fluorescently labeled molecule is determined in each frame of a time-lapse movie. From these positions, the ensemble-averaged mean-square displacement (MSD)

$$\langle {\left(\overrightarrow{R}\left(\tau \right)-\overrightarrow{R}\left(0\right)\right)}^2\rangle$$

can be calculated and used to classify the behavior as normal diffusion (when the MSD scales linearly with time interval τ) or anomalous diffusion (when the MSD scales nonlinearly) (4–6). Anomalous subdiffusion is characterized by a power-law scaling: MSD ∼τ^α, where 0 < α < 1. This type of motion has been observed for endogenous granules and chromosomal loci in many different cell types (7–16).

Although identifying anomalous behavior is an important step, the challenge now lies in determining the underlying mechanism. Several possible biological mechanisms, including binding interactions (17), cytoskeletal obstacles (18,19), and cytoplasmic viscoelasticity (20), can give rise to anomalous subdiffusion in the cell. These physiological scenarios, which are not mutually exclusive, can have various kinetic consequences on molecular motion. Thus, in addition to biological perturbations, one approach to investigate the origin of anomalous subdiffusion is to identify mathematical models that describe a molecule's kinetic behavior. Three distinct models—continuous time random walk (CTRW), obstructed diffusion, and fractional Langevin motion (fLm)—have been developed to explore different sources of anomalous diffusion (4,5).

We note that these models do not necessarily correspond to unique biological mechanisms. In a CTRW, a particle moves anomalously due to a broad distribution in waiting times between jumps (21). Obstructed diffusion occurs in spatially disordered media, where a particle encounters obstacles (22). Finally, a particle undergoing fLm exhibits long-range temporal correlations in its trajectory. This “memory” leads to anomalous diffusion (23). Despite distinct statistical properties, each of these models predicts the same long-time ensemble-averaged behavior. Therefore, the ensemble-averaged MSD alone cannot distinguish between these models. Recently, there has been much effort to develop additional metrics that can identify the kinetic origin of anomalous subdiffusion (15,21,24–28).

Previously, we identified the velocity autocorrelation function (C_υ),

$$C_v^{\left(\delta \right)}\left(\tau \right)=\langle \overrightarrow{v}\left(t+\tau \right)·\overrightarrow{v}\left(t\right)\rangle ,$$ (1)

where

$$\overrightarrow{v}\left(t\right)=\frac{1}{\delta }\left[\overrightarrow{R}\left(t+\delta \right)-\overrightarrow{R}\left(t\right)\right]$$

is the molecule's velocity, as a diagnostic tool that can distinguish among distinct mechanisms for anomalous subdiffusion (15,20). Specifically, a negative peak in C_υ is indicative of an fLm process because the elastic properties of the medium induce antipersistent behavior in a molecule's trajectory. However, a negative C_υ can also arise in other contexts. For example, large errors in localization (29), which are common for biological samples with poor signal-to-noise (S/N) ratios, and extreme spatial confinement (30) can each generate a negative peak in C_υ. If not properly identified, these alternative sources of an fLm-like signature can lead one to incorrectly conclude that a molecule behaves subdiffusively due to a viscoelastic medium. Here we discuss how localization error and confinement affect C_υ and suggest criteria for determining when these effects are (or are not) responsible for generating a negative peak in C_υ from experimental data sets.

Methods

Tracking of chromosomal loci and RNA-protein particles was performed as described in Weber et al. (15). Briefly, live bacterial cells containing fluorescently tagged loci or particles were imaged with a 200-ms exposure time (t_E) at frame intervals (t_F) ranging from 1 s to 10 min. The position of a fluorescent focus was determined by nonlinear least-squares fitting to a two-dimensional Gaussian function. Calculations of the ensemble-averaged mean-square displacement and velocity autocorrelation function were done using custom-written software in MATLAB (The MathWorks, Natick, MA). Brownian dynamics simulations were performed as described in Weber et al. (20).

Results and Discussion

Effect of localization error on C_υ

SPT experiments are inherently limited by the accuracy with which a particle's position can be determined. Many techniques have been developed to find the position of a diffraction-limited molecule in a fluorescence image (31). Regardless of the method used, there will be some error in the measured position such that

$$\overrightarrow{R}\left(t\right)={\overrightarrow{R}}_{true}\left(t\right)+{\overrightarrow{ϵ}}_t,$$

where ${\overrightarrow{R}}_{true}\left(t\right)$ is the true position of the molecule at time t and ${\overrightarrow{\mathit{ϵ}}}_t$ is the localization error at that time. This measurement uncertainty is equivalent to adding Gaussian noise of mean zero and variance $\langle {\overrightarrow{\mathit{ϵ}}}^2\rangle$ to each true position (32,33). The magnitude of the localization error depends on the S/N of the image (34,35). Bright molecules against a low background will have a smaller localization error than dim molecules with high background. When $\overrightarrow{\mathit{ϵ}}$ is comparable to the root mean-square displacement, then the molecule's MSD will appear subdiffusive at short times when plotted on log-log axes, even for a diffusive process (36).

Just as localization error can lead to apparent subdiffusion in the MSD (36), it can also generate misleading artifacts in C_υ. Specifically, large localization errors will increase the correlation at zero time-lag and decrease the correlation when the time-lag τ equals the time over which the velocity is calculated, δ. Note that δ is typically equal to t_F, the time between successive frames in a movie, but we define it more generally, because varying this value is useful in distinguishing the effects of localization error, confinement, and medium elasticity on C_υ (see below). The effects of localization error can be seen by writing C_υ in terms of true positions and localization errors, rather than the measured positions, and expanding the averaged quantity:

$$C_v^{\left(\delta \right)}\left(\tau \right)=\frac{1}{{\delta }^2}\langle \left(\overrightarrow{R}\left(\tau +\delta \right)-\overrightarrow{R}\left(\tau \right)\right)·\left(\overrightarrow{R}\left(\delta \right)-\overrightarrow{R}\left(0\right)\right)\rangle ,$$ (2)

$$=\frac{1}{{\delta }^2}\langle \left[{\overrightarrow{R}}_{true}\left(\tau +\delta \right)+{\overrightarrow{\mathit{ϵ}}}_{\tau +\delta }-\left({\overrightarrow{R}}_{true}\left(\tau \right)+{\overrightarrow{\mathit{ϵ}}}_{\tau }\right)\right]·\left[{\overrightarrow{R}}_{true}\left(\delta \right)+{\overrightarrow{\mathit{ϵ}}}_{\delta }-\left({\overrightarrow{R}}_{true}\left(0\right)+{\overrightarrow{\mathit{ϵ}}}_0\right)\right]\rangle ,$$ (3)

$$=\frac{1}{{\delta }^2}\langle \left({\overrightarrow{R}}_{true}\left(\tau +\delta \right)-{\overrightarrow{R}}_{true}\left(\tau \right)\right)·\left({\overrightarrow{R}}_{true}\left(\delta \right)-{\overrightarrow{R}}_{true}\left(0\right)\right)\rangle +\frac{1}{{\delta }^2}\langle \left({\overrightarrow{R}}_{true}\left(\tau +\delta \right)-{\overrightarrow{R}}_{true}\left(\tau \right)\right)·\left({\overrightarrow{\mathit{ϵ}}}_{\delta }-{\overrightarrow{\mathit{ϵ}}}_0\right)\rangle +\frac{1}{{\delta }^2}\langle \left({\overrightarrow{\mathit{ϵ}}}_{\tau +\delta }-{\overrightarrow{\mathit{ϵ}}}_{\tau }\right)·\left({\overrightarrow{R}}_{true}\left(\delta \right)-{\overrightarrow{R}}_{true}\left(0\right)\right)\rangle +\frac{1}{{\delta }^2}\langle \left({\overrightarrow{\mathit{ϵ}}}_{\tau +\delta }-{\overrightarrow{\mathit{ϵ}}}_{\tau }\right)·\left({\overrightarrow{\mathit{ϵ}}}_{\delta }-{\overrightarrow{\mathit{ϵ}}}_0\right)\rangle .$$ (4)

For a diffusive process, the second and third terms in the expansion (Eq. 4) are equal to zero. Because the true positions and localization errors are uncorrelated and both have a mean of zero, i.e., $\langle {\overrightarrow{R}}_{true}\left(t\right)\rangle =0$ and $\langle {\overrightarrow{\mathit{ϵ}}}_t\rangle =0$, then $\langle {\overrightarrow{R}}_{true}\left(t\right)·{\overrightarrow{\mathit{ϵ}}}_t\rangle =0$. Removing these terms, we can reduce our expression to

$$C_{\upsilon }^{\left(\delta \right)}\left(\tau \right)=\frac{1}{{\delta }^2}\langle \left({\overrightarrow{R}}_{true}\left(\tau +\delta \right)-{\overrightarrow{R}}_{true}\left(\tau \right)\right)·\left({\overrightarrow{R}}_{true}\left(\delta \right)-{\overrightarrow{R}}_{true}\left(0\right)\right)\rangle +\frac{1}{{\delta }^2}\left({\overrightarrow{\mathit{ϵ}}}_{\tau +\delta }+{\overrightarrow{\mathit{ϵ}}}_{\tau }\right)·\left({\overrightarrow{\mathit{ϵ}}}_{\delta }+{\overrightarrow{\mathit{ϵ}}}_0\right).$$ (5)

At zero time-lag,

$$C_{\upsilon }^{\left(\delta \right)}\left(\tau =0\right)=\frac{1}{{\delta }^2}\left[\langle {\left({\overrightarrow{R}}_{true}\left(\delta \right)-{\overrightarrow{R}}_{true}\left(0\right)\right)}^2\rangle +2\langle {\overrightarrow{\mathit{ϵ}}}^2\rangle \right],$$ (6)

$$=\frac{1}{{\delta }^2}\left[4D\left(\delta -\frac{1}{3}{t}_E\right)+2\langle {\overrightarrow{\mathit{ϵ}}}^2\rangle \right],$$ (7)

where

$${\langle \left({\overrightarrow{R}}_{true}\left(\delta \right)-{\overrightarrow{R}}_{true}\left(0\right)\right)}^2\rangle =4D\left(\delta -\frac{1}{3}{t}_E\right)$$

is the MSD in two dimensions at time-lag δ with diffusion coefficient D and finite exposure time t_E (29,35,37,38). Localization error causes the apparent correlation at τ = 0 to be greater than the true value. This deviation can lead to an overestimation of D. At the fast acquisition limit, when t_E → 0, this result is equivalent to that already described by Martin et al. (36) for the MSD.

The more problematic consequence of localization error occurs when τ = δ, where

$$C_v^{\left(\delta \right)}\left(\tau =\delta \right)=\frac{1}{{\delta }^2}\left[\langle \left({\overrightarrow{R}}_{true}\left(2\delta \right)-{\overrightarrow{R}}_{true}\left(\delta \right)\right)·\left({\overrightarrow{R}}_{true}\left(\delta \right)-{\overrightarrow{R}}_{true}\left(0\right)\right)\rangle -\langle {\overrightarrow{\mathit{ϵ}}}^2\rangle \right],$$ (8)

$$=\frac{1}{{\delta }^2}\left[\frac{1}{3}D{t}_E-\langle {\overrightarrow{\mathit{ϵ}}}^2\rangle \right].$$ (9)

The positive correlation (1/3 Dt_E) arises from averaging the positions of a particle as it moves during the finite exposure time (29,37,38). When t_E is small compared to δ, the first term is negligible. Thus, a large localization error can produce a negative value for C_υ when the time-lag equals the temporal resolution of the experiment, even for a diffusive process. This artifact raises questions as to the usefulness of C_υ as a diagnostic tool. If a negative peak in C_υ does not unambiguously correspond to a viscoelastic medium, as was originally proposed (15), then C_υ cannot reliably distinguish among distinct anomalous mechanisms.

Nevertheless, if the negative peak in C_υ arises from localization error rather than memory, then the magnitude of $C_{\upsilon }^{\left(\delta \right)}\left(\tau =\delta \right)$ should decrease as δ increases because the localization error in the numerator of Eq. 9 is independent of time. For experimental data sets, velocity measurements can be resampled such that δ becomes any integer multiple of the frame interval, t_F: δ = n × t_F, where 1 ≤ n ≤ N/2 and N is the total number of frames in the movie. To facilitate comparisons between simulations and experimental data using different probes, we normalize our calculations by $C_{\upsilon }^{\left(\delta \right)}\left(\tau =0\right)$ (Eq. 7). Thus, the negative peak due to localization error in our normalized C_υ will decay more slowly than 1/δ² but should still approach zero as δ → ∞.

We confirmed this prediction by simulations. We simulated movies of diffusing particles with varying S/N, as described in Weber et al. (15), and calculated C_υ for integer values of δ. As shown in Fig. 1 A, C_υ ≈ 0 for all time-lags τ ≥ δ when S/N is large. However, a sharp negative peak is observed for short τ at small S/N (Fig. 1 D). Importantly, this negative peak decays as δ increases. This δ-dependent decay is characteristic of the artifactual negative autocorrelation caused by localization error.

Figure 1.

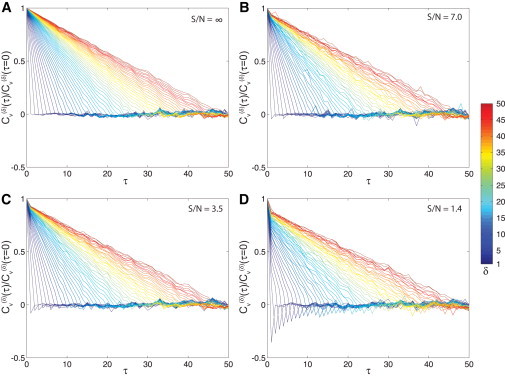
Simulation results for $C_{\upsilon }^{\left(\delta \right)}\left(\tau \right)/C_{\upsilon }^{\left(\delta \right)}\left(\tau =0\right)$ versus τ for particles undergoing normal diffusion with a S/N of (A) ∞, (B) 7.0, (C) 3.5, or (D) 1.4, where S/N $\approx \sqrt{\text{MSD}(\tau =0)}/\left|\overrightarrow{\mathit{ϵ}}\right|$ and $t_E=0$. The term $C_{\upsilon }^{\left(\delta \right)}\left(\tau \right)$ was calculated for integer values of δ from 1 to 50 (blue to red).

In contrast, the negative peak in C_υ of chromosomal loci in Escherichia coli persists for all δ (Fig. 2 A). This observation is consistent with the ensemble-averaged MSD, which exhibits robust subdiffusive scaling for all timescales examined (15). Therefore, the negative value of C_υ observed in our experiments is not caused by localization error. RNA-protein particles also exhibit a negative peak in C_υ that does not appear to decay systematically, although the exact δ-dependence is difficult to assess due to the statistical noise inherent in this smaller dataset (n = 323 vs. n = 7903 for chromosomal loci; see Fig. 2 B).

Figure 2.

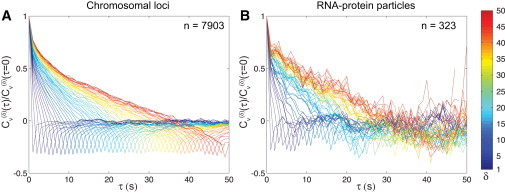
Experimental measurements of $C_{\upsilon }^{\left(\delta \right)}\left(\tau \right)/C_{\upsilon }^{\left(\delta \right)}\left(\tau =0\right)$ versus τ for (A) chromosomal loci and (B) RNA-protein particles, calculated for integer values of δ from 1 to 50 s (blue to red).

In conclusion, the velocity autocorrelation function can serve as a diagnostic tool to distinguish localization error from other causes of apparent anomalous subdiffusion. The artifactual negative peak in C_υ that arises due to localization error occurs in the same noise range that causes the MSD to appear subdiffusive (36), even for truly diffusive processes. Thus, this problem should not arise when the S/N is high and localization error is low. To experimentally determine whether the S/N is sufficiently high, the ensemble-averaged MSD of a live, dynamic sample can be compared to a fixed, stationary sample. Any apparent motion in the fixed sample will be due to measurement errors. We note that measurement errors can arise not only from localization error, but also stage drift. Drift can be corrected either by subtracting the motion of bright fiduciary markers (39) or by correlation analysis of fixed samples (33). If the apparent motion of the fixed sample is small compared to the motion in the live sample, then C_υ can be used reliably to identify fLm anticorrelations.

We showed previously that the error in our experimental measurements (which includes both localization error and stage drift) was more than an order-of-magnitude smaller than the motion of chromosomal loci (15). Thus, the subdiffusive scaling and negative C_υ that we observe arises from an fLm mechanism and is not simply an experimental artifact. Furthermore, we have shown here that varying the velocity discretization δ can also be used to identify the true source of a negative value of C_υ.

Effect of confinement on C_υ

Burov et al. (30) recently reported that a continuous time random walk (CTRW) process can exhibit a negative peak in C_υ when confined to a finite space. From this observation, the authors concluded that C_υ could not distinguish between CTRW and fLm mechanisms under confinement. Indeed, confinement and memory can both generate negative peaks. However, the shape of $C_{\upsilon }^{\left(\delta \right)}\left(\tau \right)$ versus τ is different in each case. In this section, we demonstrate that examination of C_υ across a range of discretizations δ can distinguish between confinement and memory as physical mechanisms generating a negative peak in C_υ.

Consider a particle moving diffusively inside a box. At short timescales, it will move freely inside the box, only rarely encountering the boundaries. Its motion will appear diffusive, with the ensemble-averaged MSD increasing linearly with time, as if the box were not present (see Fig. 3 A, inset). At intermediate timescales, when the distance traveled is comparable to the size of the box, the particle will begin to experience correlations as it reflects off the boundaries. Here, its MSD will cross over from diffusive to subdiffusive scaling and its velocity autocorrelation function will exhibit negative peaks. Finally, at long timescales, the particle will bounce off the walls back-and-forth many times, and so its motion will become uncorrelated again. However, the confining boundary prevents the particle from moving outside the box, so the MSD plateaus to a constant value.

Figure 3.

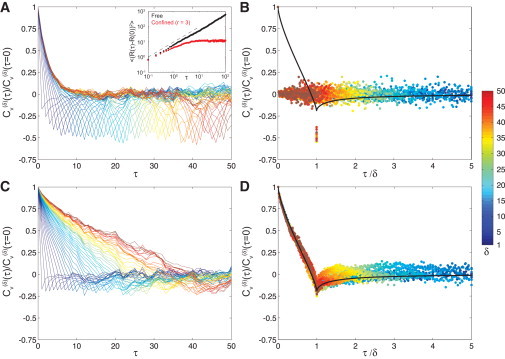
Simulation results for $C_{\upsilon }^{\left(\delta \right)}\left(\tau \right)/C_{\upsilon }^{\left(\delta \right)}\left(\tau =0\right)$ for (A and B) a confined particle undergoing normal diffusion and (C and D) a free particle undergoing fLm, with δ ranging from 1 to 50 (blue to red). Panels A and C display $C_{\upsilon }^{\left(\delta \right)}\left(\tau \right)/C_{\upsilon }^{\left(\delta \right)}\left(\tau =0\right)$ versus τ. In panels B and D, $C_{\upsilon }^{\left(\delta \right)}\left(\tau \right)/C_{\upsilon }^{\left(\delta \right)}\left(\tau =0\right)$ is plotted against the rescaled time-lag, τ/δ. (Solid black lines in panels B and D are the analytical theory for an fLm process with α = 0.7; see Weber et al. (20)). (Inset) Ensemble-averaged MSD for a particle undergoing normal diffusion either free (black) or confined within a sphere of radius 3 (red).

At these long timescales, $C_{\upsilon }^{\left(\delta \right)}\left(\tau \right)$ quickly decays from 1 at τ = 0 to 0 for all τ ≠ δ (Fig. 3 A). When τ = δ, a sharp peak of −0.5 occurs due to the confined geometry. Because the particle explores the entire box, the average position of the particle at any time t is in the middle of the box,

$$\langle \overrightarrow{R}\left(t\right)\rangle =\frac{L}{2},$$

where L is the length of the box. Furthermore, its position at time t will be uncorrelated from its position at time t′, such that

$$\langle \overrightarrow{R}\left(t\right)·\overrightarrow{R}\left(t^{\prime }\right)\rangle =\langle \overrightarrow{R}\left(t\right)\rangle \langle \overrightarrow{R}\left(t^{\prime }\right)\rangle =\frac{L^2}{4},$$

and finally, because

$${\int }_0^L{x}^{2}dx=\frac{L^3}{3},$$

then $\langle \overrightarrow{R}\left(t\right)·\overrightarrow{R}\left(t\right)\rangle =L^3/3$.

Thus, we can calculate $C_{\upsilon }^{\left(\delta \right)}\left(\tau =\delta \right)/C_{\upsilon }^{\left(\delta \right)}\left(\tau =0\right)$ as follows. In the numerator,

$$C_{\upsilon }^{\left(\delta \right)}\left(\tau =\delta \right)=\frac{1}{{\delta }^2}\langle \left(\overrightarrow{R}\left(2\delta \right)-\overrightarrow{R}\left(\delta \right)\right)·\left(\overrightarrow{R}\left(\delta \right)-\overrightarrow{R}\left(0\right)\right)\rangle ,$$ (10)

$$=\frac{1}{{\delta }^2}\langle \overrightarrow{R}\left(2\delta \right)·\overrightarrow{R}\left(\delta \right)\rangle -\frac{1}{{\delta }^2}\langle \overrightarrow{R}\left(2\delta \right)·\overrightarrow{R}\left(0\right)\rangle -\frac{1}{{\delta }^2}\langle \overrightarrow{R}\left(\delta \right)·\overrightarrow{R}\left(\delta \right)\rangle +\frac{1}{{\delta }^2}\langle \overrightarrow{R}\left(\delta \right)·(\overrightarrow{R}\left(0\right)\rangle ,$$ (11)

$$=\frac{1}{{\delta }^2}\left[\frac{L^2}{4}-\frac{L^2}{4}-\frac{L^3}{3}+\frac{L^2}{4}\right],$$ (12)

$$=\frac{3L^2-4L^3}{12{\delta }^2}.$$ (13)

In the denominator,

$$C_{\upsilon }^{\left(\delta \right)}\left(\tau =0\right)=\frac{1}{{\delta }^2}\langle \left(\overrightarrow{R}\left(\delta \right)-\overrightarrow{R}\left(0\right)\right)·\left(\overrightarrow{R}\left(\delta \right)-\overrightarrow{R}\left(0\right)\right)\rangle ,$$ (14)

$$=\frac{1}{{\delta }^2}\langle \overrightarrow{R}\left(\delta \right)·\overrightarrow{R}\left(\delta \right)\rangle -\frac{1}{{\delta }^2}\langle \overrightarrow{R}\left(\delta \right)·\overrightarrow{R}\left(0\right)\rangle -\frac{1}{{\delta }^2}\langle \overrightarrow{R}\left(0\right)·\overrightarrow{R}\left(\delta \right)\rangle +\frac{1}{{\delta }^2}\langle \overrightarrow{R}\left(0\right)·(\overrightarrow{R}\left(0\right))\rangle ,$$ (15)

$$=\frac{1}{{\delta }^2}\left[\frac{L^3}{3}-\frac{L^2}{4}-\frac{L^2}{4}+\frac{L^3}{3}\right],$$ (16)

$$=\frac{4L^3-3L^2}{6{\delta }^2}.$$ (17)

Finally,

$$\frac{C_{\upsilon }^{\left(\delta \right)}\left(\tau =\delta \right)}{C_{\upsilon }^{\left(\delta \right)}\left(\tau =0\right)}=-\frac{1}{2}.$$ (18)

This negative correlation arises regardless of the mechanism of motion, and will appear for diffusive and subdiffusive processes alike. In Fig. 3 A, we plot $C_{\upsilon }^{\left(\delta \right)}\left(\tau \right)/C_{\upsilon }^{\left(\delta \right)}\left(\tau =0\right)$ against τ for integer values of δ from Brownian dynamics simulations of a diffusive particle moving in a confinement sphere with radius r = 3. The ensemble-averaged MSD is shown in the inset, compared with a free (unconfined) particle. In Fig. 3 B, we rescale the x axis by δ to collapse the individual curves. We plot these data as points, rather than lines, to avoid the false appearance of continuity. Finally, we plot the analytical form of C_υ for an fLm mechanism (see Eq. 1 in Weber et al. (15)) where α = 0.7, demonstrating that the shape of the confined C_υ falls below the fLm C_υ for time-lags τ /δ < 1.

We contrast these results for a confined diffusive particle with the same analysis of a free (unconfined) particle moving via fLm. As shown in Fig. 3 C, $C_{\upsilon }^{\left(\delta \right)}\left(\tau \right)/C_{\upsilon }^{\left(\delta \right)}\left(\tau =0\right)$ decays slowly from 1 and reaches a negative value that depends on α (see Eq. 1 in Weber et al. (15)). When fLm C_υ is plotted against a rescaled time-lag, τ /δ, the individual curves collapse onto a universal curve that matches our analytical result (Fig. 3 D). Thus, comparison of the shape of C_υ for different values of δ to the analytical expression for C_υ of an fLm process can distinguish between confinement and memory.

Now we repeat this analysis on experimental data from chromosomal loci in E. coli. At timescales of ∼1–100 s, loci move distances smaller than the size of the cell, such that their motion is not affected by the cell wall/membrane. This can be seen from the constant power-law scaling of the ensemble-averaged MSD (Fig. 4). The difference in magnitude of motion along the length and width axes of the cell has been observed before in E. coli (12) and Vibrio cholerae (11) and may reflect an underlying structural anisotropy in the bacterial chromosome. At longer times, τ > 100 s, the MSD scaling changes as locus motion extends to lengthscales comparable to cell size. In untreated cells, the MSD becomes superdiffusive in the length direction due to cell elongation. In the width direction, the MSD reaches a plateau because the cell-width remains constant over the cell cycle. However, when cell growth is inhibited by the antibiotic rifampin, the MSD reaches a plateau in both directions after ∼1000 s. Rifampin also increases the apparent diffusion coefficient D_app, as shown previously (15). Thus, we can observe locus motion in three different regimes: 1) preconfined, from 1 to 100 s; 2) crossover, from 20 to 2000 s; and 3) confined, from 600 to 28,000 s.

Figure 4.

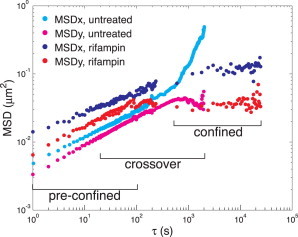
Ensemble-averaged MSD for chromosomal loci in untreated and rifampin-treated cells. The MSD was calculated separately along the length (x) and width (y) axes of the cell.

In Fig. 5, we plot $C_v^{\left(\delta \right)}\left(\tau \right)/C_v^{\left(\delta \right)}\left(\tau =0\right)$ for the 84′ locus in E. coli cells against τ for a range of δ. At short times, when loci are not yet confined, C_υ decays slowly to a negative peak of −0.31 ± 0.19 (Fig. 5 A). When the time-lag is rescaled, individual C_υ curves collapse onto a universal curve, showing excellent agreement with our analytical result for fLm with α = 0.4 (Fig. 5 B). These results are indistinguishable from those for loci in rifampin-treated cells at the same timescales (data not shown).

Figure 5.

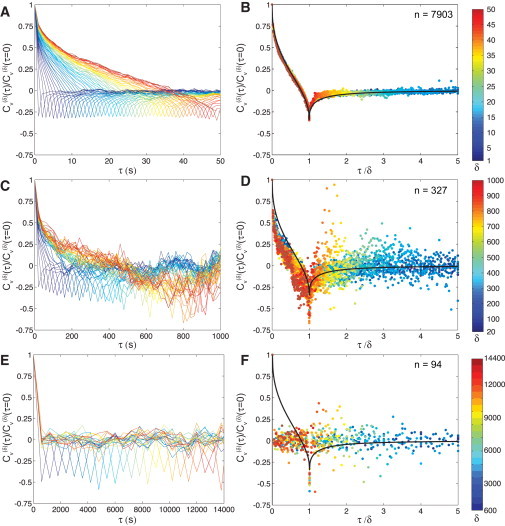
Experimental measurements of $C_{\upsilon }^{\left(\delta \right)}\left(\tau \right)/C_{\upsilon }^{\left(\delta \right)}\left(\tau =0\right)$ for chromosomal loci in the (A and B) preconfined (C and D) crossover and (E and F) confined regimes. In panels A, C, and E, $C_{\upsilon }^{\left(\delta \right)}\left(\tau \right)/C_{\upsilon }^{\left(\delta \right)}\left(\tau =0\right)$ is plotted against time-lag τ. In panels B, D, and F, the time-lag has been rescaled by δ. Colors (blue to red) represent different values of δ: (A and B) 1–50 s, at 1 s intervals; (C and D) 20–1000 s, at 20 s intervals; and (E and F) 600–13,800 s, at 600 s intervals. (Solid black lines in B, D, and F are the analytical theory for an fLm process with α = 0.4.) C_υ in panels A and B was calculated along both axes of untreated cells; in panels C–F, it was calculated along the width (y) axis of untreated (C and D) or rifampin-treated (E and F) cells.

At intermediate timescales, when the MSD in the width axis crosses over from a subdiffusive power-law to a plateau (Fig. 4), the peak of C_υ becomes more negative as the curve decays more rapidly (Fig. 5 C). Here we plot $C_{\upsilon }^{\left(\delta \right)}\left(\tau \right)/C_{\upsilon }^{\left(\delta \right)}\left(\tau =0\right)$ along the width axis for untreated cells. These results are analogous to those presented in Fig. 3 A for a confined diffusive particle, except that the value of $C_{\upsilon }^{\left(\delta \right)}\left(\tau =\delta \right)$ for short τ is initially negative, and not zero, because of memory. The collapsed curves (Fig. 5 D) show poorer agreement with the theory, particularly at time-lags τ /δ < 1.

Finally, at long timescales, when the MSD plateaus in rifampin-treated cells (Fig. 4), C_υ decays rapidly to 0 and reaches a peak of ∼−0.5 when τ = δ (Fig. 5 E). The rescaled curves do not overlap and are significantly lower than predicted by fLm for τ = δ < 1 (Fig. 5 F). Thus, at long timescales, confinement can mask the correlations due to memory. Indeed, as Burov et al. (30) conclude, C_υ cannot distinguish between subdiffusive (or diffusive) mechanisms at timescales for which the MSD is plateaued due to confinement. However, if shorter timescales are accessible, then C_υ can serve as a diagnostic tool. If C_υ exhibits negative peaks at timescales where the MSD has a power-law scaling, then these correlations arise from memory due to fLm and not confinement. A CTRW in this preconfined regime would produce $C_{\upsilon }^{\left(\delta \right)}\left(\tau =\delta \right)=0$.

Furthermore, our analysis demonstrates the importance of examining $C_{\upsilon }^{\left(\delta \right)}\left(\tau \right)$ over a range of discretizations. A single curve with a negative peak can be difficult to attribute to localization error, confinement, or memory. However, the collapse of many curves when the time-lag is rescaled to τ/δ is distinct for each case and can be distinguished experimentally, as shown in Fig. 5.

Conclusion

As new methods are developed to analyze SPT data, it is important to understand the regimes within which these metrics are valid and how experimental uncertainties or additional biological processes may affect the measurement. Here, we have explored three phenomena—localization error, confinement, and subdiffusion by fLm—that each produce a negative peak in C_υ. Given only a single C_υ curve, it is difficult to interpret what the underlying cause of anticorrelation is. However, this ambiguity can be resolved by examining the shape of C_υ across a range of discretizations δ. Furthermore, the behavior of the ensemble-averaged MSD can also be used to identify the source of a negative peak in C_υ.

Fig. 6 depicts the ensemble-averaged MSD and C_υ in three different regimes: 1) noise-limited; 2) subdiffusive; and 3) confined. In the noise-limited regime, the slope of the ensemble-averaged MSD is shallow but increases at longer times. C_υ has a sharp negative peak at short time-lags that decays as δ increases. In the subdiffusive regime, the ensemble-averaged MSD follows a power-law and C_υ has a stable negative peak independent of δ. Finally, in the confinement regime, the ensemble-averaged MSD has reached a plateau and is constant with τ. C_υ decays quickly to zero except for a −0.5 value at τ = δ.

Figure 6.

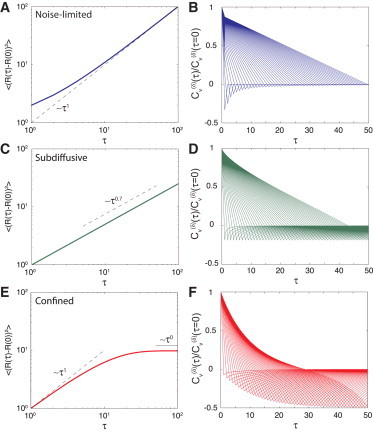
Ensemble-averaged MSD and $C_{\upsilon }^{\left(\delta \right)}\left(\tau \right)/C_{\upsilon }^{\left(\delta \right)}\left(\tau =0\right)$ for a population of molecules in three different regimes: noise-limited, subdiffusive, and confined. (A) Ensemble-averaged MSD versus τ and (B) C_υ in the noise-limited regime, where $\overrightarrow{\mathit{\epsilon }}=1$. (C) Ensemble-averaged MSD versus τ and (D) C_υ in the subdiffusive regime, where α = 0.7. (E) Ensemble-averaged MSD versus τ and (F) C_υ in the confined regime, where L = 60.

In conclusion, the velocity autocorrelation function can serve as a diagnostic tool. The effects of localization error, confinement, and medium elasticity can be distinguished by analyzing the shape of C_υ as a function of δ. Applying this analysis to experimental data, we can unambiguously conclude that chromosomal loci in E. coli move subdiffusively by an fLm mechanism at timescales of 1–100 s, and become confined at timescales longer than 1000 s. Calculation of C_υ across a range of values of δ should be a useful tool in identifying the source of anticorrelations in the trajectories of molecules inside living cells.