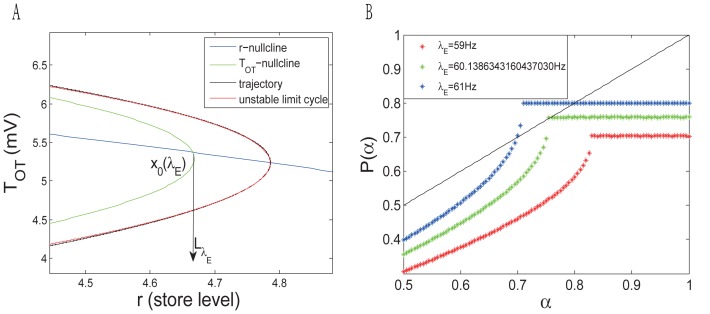
Figure 6.
(A) Establishment of a coordinate system on the half line 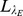 with the origin
with the origin 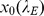 . Here,
. Here, 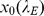 is the equilibrium point and
is the equilibrium point and 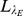 is transversal to the vector field in the neighborhood of
is transversal to the vector field in the neighborhood of 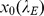 . Note that both
. Note that both 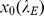 and
and 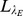 depend continuously on
depend continuously on 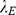 ; (B) Curves of the Poincaré map
; (B) Curves of the Poincaré map 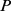 . Each intersection between the curves and the black line
. Each intersection between the curves and the black line 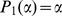 corresponds to a fixed point of
corresponds to a fixed point of 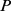 as well as to a limit cycle of the system (8). For
as well as to a limit cycle of the system (8). For 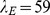 Hz, the curve has no intersection with the black line, so that there is no limit cycle. At higher values of
Hz, the curve has no intersection with the black line, so that there is no limit cycle. At higher values of 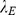 , the curve moves upward; it first intersects with the black line at
, the curve moves upward; it first intersects with the black line at 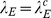 , where a single semi-stable limit cycle emerges. As
, where a single semi-stable limit cycle emerges. As 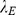 increases to
increases to 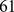 Hz, two bifurcated limit cycles appears. Here, one cycle is stable characterized by the quantity
Hz, two bifurcated limit cycles appears. Here, one cycle is stable characterized by the quantity 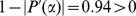 at one fixed point, and the other cycle is unstable with the quantity
at one fixed point, and the other cycle is unstable with the quantity 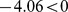 at the other fixed point.
at the other fixed point.