Abstract
Progress in understanding protein folding relies heavily upon an interplay between experiment and theory. In particular, readily interpretable experimental data are required that can be meaningfully compared to simulations. According to standard mutational φ analysis, the transition state for Protein L contains only a single hairpin. However, we demonstrate here using ψ analysis with engineered metal ion binding sites that the transition state is extensive, containing the entire four-stranded β sheet. Underreporting of the structural content of the transition state by φ analysis also occurs for acyl phosphatase1, ubiquitin2 and BdpA3. The carboxy terminal hairpin in the transition state of Protein L is found to be non-native, a significant result that agrees with our PDB-based backbone sampling and all-atom simulations. The non-native character partially explains the failure of accepted experimental and native-centric computational approaches to adequately describe the transition state. Hence, caution is required even when an apparent agreement exists between experiment and theory, thus highlighting the importance of having alternative methods for characterizing transition states.
Keywords: Phi analysis, Psi analysis, metal binding, bi-histidine, protein folding
Introduction
The IgG binding domain of protein L (Protein L) contains two hairpins and a central helix and has been a test bed for many experimental and theoretical studies of folding 4; 5; 6; 7; 8; 9; 10; 11; 12; 13; 14. Mutational φ analysis experiments indicate that the folding transition state ensemble (TSE) contains only the amino terminal hairpin4; 5; 6; 7 (Fig 1). The TSE of a protein with the same α/β fold, Protein G, also is assigned by φ analysis to have a single hairpin, but this hairpin is located at the carboxy terminus15, a behavior attributed to different properties of the turn sequences16; 17. The difference between the TSEs of these two proteins is cited as an example where the specific sequence, rather than just the protein’s topology, influences the folding pathway. A variety of computational studies support this view 8; 9; 10; 11; 12; 14.
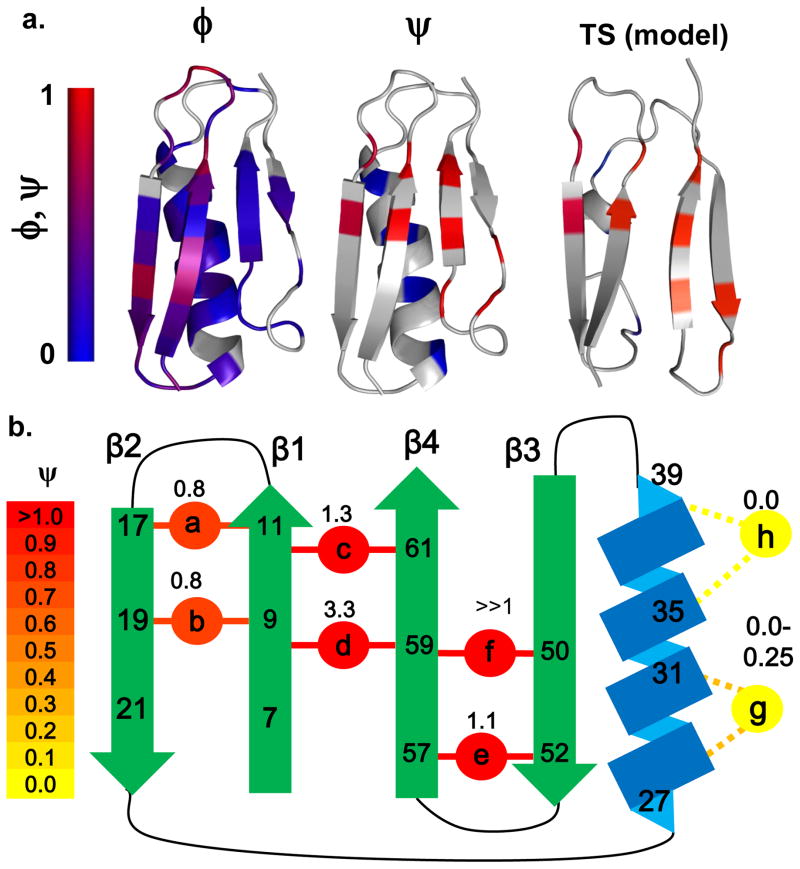
Fig. 1. BiHis sites, ψ and φ values, and TSE for Protein L.
a. φ and ψ values mapped onto Protein L. The ψ are obtained from the present study, while the φ are from ref. 7. When multiple mutations are studied at a particular site, more emphasis is placed on the X-to-Ala and Ala-to-Gly comparisons for core and helical mutations, respectively. The model of the TSE is created by docking the two hairpins using the ItFix protocols. b. The locations of the biHis sites and ψ values are shown (each site is studied individually). Renderings created in PyMol.
Despite this broad consensus, we decided to reexamine the folding behavior of Protein L because a TSE with only a single hairpin seems inordinately small. A hairpin scarcely defines Protein L’s topology, yet this protein obeys the well-known correlation between folding rate and topology (relative contact order, RCO)18; 19. Our studies of three other proteins with disparate RCOs, indicate that their TSEs acquire a similar level of native topology, RCOTSE ≈ 0.7·RCONative 3; 20; 21; 22; 23. If this relationship is generally applicable, it would provide a simple rationalization for the kf-RCO correlation, as well as a constraint for possible TSE structures of other proteins.
In the case of Protein L, the presence of only a single hairpin in the TSE equates to a RCO fraction of only 25%, and even the inclusion of the helix would increase the RCO only to 40%. In order to achieve an RCO fraction close to 70%, the TSE must minimally include long-range contacts between the amino and carboxy terminal strands. Furthermore, whereas a 1:1 relationship between hydrogen bond content and surface burial is found in the TSEs of other proteins24; 25, the hydrogen bond content of a single hairpin is grossly inadequate to match the surface burial of the highly collapsed TSE of Protein L as determined by the denaturant dependence of the folding rates.
Here we employ ψ analysis26 to characterize the TSE structure of Protein L. ψ is well suited for determining the structure because the methodology directly identifies pairwise residue-residue contacts. The methodology employs biHistidine (biHis) metal ion binding sites on the surface of protein which are stabilized by the addition of metal ions. The ion-induced stabilization of the TSE relative to the native state is represented by the ψ value which is high if the biHis site is present in the TSE. Data for a multitude of biHis sites (individually introduced) can be used to generate structural models of the TSE analogous to the use of NOE distance constraints in NMR-based structure determination.
These experiments demonstrate that Protein L’s TSE contains the entire four stranded β sheet. Although the amino terminal hairpin is native-like, the carboxy hairpin and the long-range interactions between the two hairpins have non-native properties. We conduct simulations of the individual hairpins using our ItFix folding algorithm where the side chains are represented by single Cβ atoms 27; 28, as well as all-atom, explicit solvent molecular dynamics (MD) simulations. Without invoking any knowledge of the native state, both methods indicate the carboxy terminal hairpin forms rapidly, but with a non-native turn. We discuss the implications of our findings with regards to TSE topology, the accuracy of φ analysis, and its ability to validate theoretical studies.
Results
ψ analysis 2; 3; 21; 22; 26; 29 proceeds by introducing biHis metal ion binding sites at positions across the protein’s surface. A total of eight sites are individually introduced into Protein L to probe the formation of the three native strand-strand pairings and the helix (Fig. 1). Upon addition of metal ions, the biHis sites stabilize strand-strand pairings or the helix because an increase in metal ion concentration stabilizes the interaction between the two histidine partners. The changes in protein’s equilibrium stability and folding activation free energy, ΔΔGeq and ΔΔGf respectively, arise from the difference in metal ion binding disassociation constants, KU, KN, and KTSE, of the biHis site in the unfolded (U) state, native (N) state, and TSE, as given by
| (1a) |
| (1b) |
These ion-induced changes in free energies are used to define the ψ value, a parameter analogous to the standard mutational φ value, although ψ is the instantaneous change as a function of metal ion,
| (2a) |
| (2b) |
To remove any potential artifacts related to the alteration of the folding behavior by the metal ion binding, a “ψ0” value is obtained by evaluating ψ in the limit of [Me2+] → 0. The ψ0 thus reflects the intrinsic degree of contact formation in the TSE when metal ions are absent. Hence, ψ analysis provides information on the conformation of the TSE prior to any ion-induced perturbation. In particular, ψ analysis probes the metal ion binding affinity of the two histidines in the TSE; e.g., if the two residues are pre-positioned to bind ions tighter in the TSE than in the native-state, this stabilization arises because the TSE adopts a non-native conformation, not because the ions induce a conformational change. This ability to identify the intrinsic folding behavior in the absence of the metal ion perturbation lacks a direct counterpart with φ analysis, which typically does not address the possible consequences of even sizable substitutions on altering the properties of the TSE.
ψ0 values of zero or unity indicate that the biHis site has the ion binding affinity found in the unfolded or native site, respectively. These values are interpreted as implying that the biHis site is absent or native-like in the TS, respectively. A fractional ψ value indicates that the biHis site either is native-like in a subpopulation of the TSE, or the site contains non-native binding affinity in the entire TSE (e.g., a distorted site with less favorable binding geometry or a flexible site that must be restricted prior to ion binding), or some combination thereof 2; 20. A more thorough description of ψ analysis is provided in the appendix.
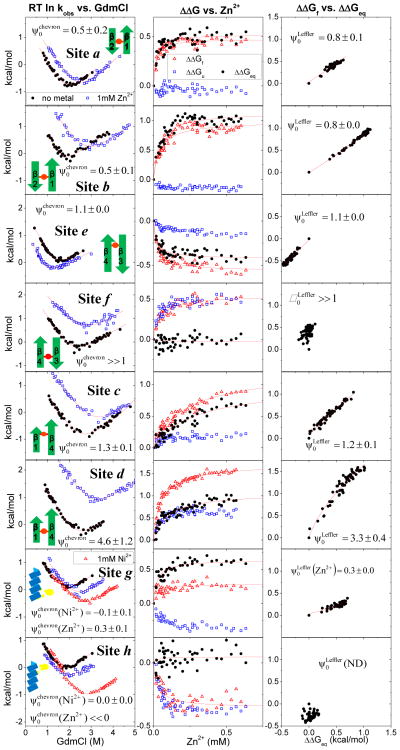
The folding properties and ψ0 value of each biHis variant are measured using two independent approaches. First, the dependence of the folding and unfolding rates on the concentration of guanidinium chloride (GdmCl) (“chevron analysis” with plots RT ln (kobserved) versus [denaturant]) are obtained in the absence and presence of 1 mM zinc or nickel ions at 22°C, pH 7.5 (Fig. 2, left panels). Second, kinetic data are taken at dozens of different metal concentrations (Fig. 2, center and right panels) under strongly folding (~0.6 M GdmCl) and strongly unfolding conditions (~ 3.5–5 M GdmCl, depending upon variant).
Fig. 2. Metal-dependent kinetic data. Left.
The denaturant chevrons in the absence of metal ions (black solid circle), in the presence of 1 mM Zn2+ (blue open square), and with Ni2+ (red open triangle). Center. Kinetics as a function of Zn2+ at fixed [GdmCl]. The changes in stability ΔΔGeq (black solid circle), folding activation energy ΔΔGf (red open triangle), and unfolding activation energy ΔΔGu (blue open square) plotted against Zn2+ concentration. Values are calculated by measuring the folding and unfolding rates at fixed low (~0.6 M) and high (~3.5–5 M) GdmCl concentrations, respectively (Table 2). The binding affinities are obtained from fitting to the Eq. 1. Right. Corresponding Leffler plots.
Using each of the two classes of data, the ψ0 value for each site is evaluated using an equation derived from Eqs. 1 & 2,
| (3) |
A value is evaluated from the changes in the folding and unfolding rates (i.e., the shift in the arms of the chevron plots) arising from the addition of 1 mM metal ion. The magnitude of the shifts generates a single (ΔΔGeq, ΔΔGf) pair. This pair is sufficient to determine ψ0 using Eq. 3. This procedure is analogous to the method for calculating φ by comparing the chevrons for the wild-type and mutant proteins.
The second, independent determination of ψ0, termed , is obtained from the fit of the ΔΔGeq versus ΔΔGf data, as presented in the Leffler plot (Fig. 2, right panel). Here, the multitude of (ΔΔGeq, ΔΔGf) points obtained using the kinetic data taken at dozens of metal ion concentrations are fit using a re-arranged form of Eq. 3, ΔΔGf = RT 1n ((1−ψ0) + ψ0eΔΔGeqRT) In addition, the metal ion dependence of ΔΔGeq and ΔΔGf (Fig. 2, central panels) and Eq. 1 are used to individually determine each of the dissociation constants, KU, KN, and KTSE (Table 1).
Table 1.
ψ values and Zn2+ dissociation constants
| Site | Mutation | KU (μM) | KN (μM) | KTSE (μM) | KU/KN | KTSE/KN | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| a | I11H T17H (β1-β2) |
0.77 ±0.07 | 0.51 ± 0.17 | 26.5 ± 3.3 | 10.8 ± 1.2 | 11.7 ± 1.3 | 2.44 ± 0.42 | 1.08 ± 0.18 | ||
| b | N9H T19H (β1-β2) |
0.75 ±0.03 | 0.48 ± 0.07 | 105 ± 11 | 14.9 ± 1.1 | 19.3 ± 1.5 | 7.02 ± 0.90 | 1.29 ± 0.14 | ||
| c | I11H K61H (β1-β4) |
1.24 ±0.07 | 1.28 ± 0.10 | 697 ± 107 | 122 ± 9 | 79.3 ± 4.8 | 5.69 ± 0.96 | 0.65 ± 0.06 | ||
| d | N9H N59H (β1-β4) |
3.33 ±0.40 | 4.64 ± 1.24 | 232 ± 21 | 36.8 ± 2.0 | 11.8 ± 0.6 | 6.30 ± 0.66 | 0.32 ± 0.02 | ||
| e | A52H T57H (β3-β4) |
1.13 ±0.03 | 1.13 ± 0.02 | 15.2 ± 1.4 | 31.4 ± 3.3 | 39.7 ± 4.3 | 0.48 ± 0.07 | 1.26 ± 0.19 | ||
| f | D50H N59H (β3-β4) |
≫1 1 | ≫1 1 | 71.5 ± 12.0 | 75.3 ± 12.9 | 28.6 ± 4.0 | 0.95 ± 0.23 | 0.38 ± 0.08 | ||
| g | K28H E32H (helix) |
0.26 ± 0.03 | 0.25 ± 0.09 (−0.05 ± 0.05)2 | 43.1 ± 6.5 | 14.5 ± 1.9 | 26.3 ± 3.7 | 2.97 ± 0.59 | 1.81 ± 0.35 | ||
| h | A35H T39H (helix) |
≪0 1 | (0.02 ± 0.004)2 | 23.3 ± 5.6 | 21.4 ± 5.1 | 42.6 ± 11.4 | 1.09 ± 0.37 | 1.99 ± 0.71 |
The metal-induced stabilization is too small to provide a well-defined ψ value.
Values in parentheses are obtained using Ni2+ ions.
Structure in Protein L’s TSE
Six biHis sites are located on the sheets, and two sites are situated along the helix. Sites a & b and e & f are located on the amino and carboxy hairpins, respectively. Sites c & d lie between the amino and carboxy strands and connect the two hairpins. Sites g and h are located in i, i+4 positions along the sole helix.
The sensitivity of folding rates to metal ion concentration indicated that Protein L’s TSE had all six biHis sites on the β sheet at least partially formed, while the helix was largely absent (Fig. 2, Tables 1,2). For Sites a and b on the amino hairpin, the histidines pairs had a near-native binding affinity with and 0.75±0.03, while was slightly lower, 0.51 ± 0.17 and 0.48 ± 0.07, respectively. These data indicated that the hairpin was formed in the TSE, although with the biHis site having slightly weaker ion binding affinity in the TSE than in the native state. This interpretation is consistent with the high values of φ measured for mutations throughout the hairpin7.
Table 2.
Equilibrium and kinetic parameters for divalent metal ion binding1
| Site | Mutation (location) | ΔΔGmut |
|
m0 ( ) | mf/m0 ( ) |
|
Metal | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| WT | NA | NA | NA | NA (1.51 ± 0.06) | 1.97 ± 0.08 (NA) | 0.73 ± 0.05 (NA) | NA | NA | |||
| a | I11H T17H (β1-β2) |
0.14 ± 0.02 | 0.88 ± 0.034 (0.70 ± 0.18) | 0.46 ± 0.17 (0.79 ± 0.05) | 2.11 ± 0.11 (1.92 ± 0.06) | 0.67 ± 0.05 (0.63 ± 0.03) | 0.77 ± 0.07 (0.51 ± 0.17) | Zn | |||
| b | N9H T19H (β1–β2) |
−0.32 ± 0.02 | 1.31 ± 0.13 (1.11 ±0.24) | 0.77 ± 0.22 (1.64 ± 0.16) | 2.38 ± 0.22 (1.68 ± 0.12) | 0.76 ± 0.11 (0.67 ± 0.08) | 0.75 ± 0.03 (0.48 ± 0.07) | Zn | |||
| c | I11H K61H (β1-β4) |
−0.45 ± 0.03 | ND (0.92 ± 0.10) | 1.03± 0.10 (1.18 ± 0.06) | 1.81 ± 0.07 (1.58 ± 0.06) | 0.65 ± 0.04 (0.68 ± 0.04) | 1.24 ± 0.07 (1.28 ± 0.10) | Zn | |||
| d | N9H N59H (β1-β4) |
0.53 ± 0.02 | 1.03 ± 0.15 (0.85 ± 0.16) | 1.63 ± 0.25 (1.88 ± 0.05) | 1.87 ± 0.11 (1.70 ± 0.07) | 0.73 ± 0.06 (0.69 ± 0.04) | 3.33 ± 0.40 (4.64 ± 1.24) | Zn | |||
| e | A52H T57H (β3-β4) |
−0.88 ± 0.02 | −0.60 ± 0.075 (−0.60 ± 0.03) | −0.76 ± 0.05 (1.11 ± 0.02) | 2.22 ± 0.07 (2.38 ± 0.11) | 0.81 ± 0.04 (0.82 ± 0.06) | 1.13 ± 0.03 (1.13 ± 0.02) 6 | Zn | |||
| f | D50H N59H (β3-β4) |
0.64 ± 0.02 | 0.21 ± 0.17 (0.03 ± 0.12) | 0.66 ± 2.47 (1.79 ± 0.10) | 1.96 ± 0.13 (1.54 ± 0.11) | 0.73 ± 0.08 (0.65 ± 0.08) | ND 7 | Zn | |||
| g | K28H E32H (helix) |
−0.46 ± 0.02 | 1.10 ± 0.04 (0.76 ± 0.24) | 0.29 ± 0.16 (1.37 ± 0.05) | 1.92 ± 0.14 (1.81 ± 0.11) | 0.69 ± 0.08 (0.66 ± 0.06) | 0.26 ± 0.03 (0.25 ± 0.09) | Zn | |||
| 1.20 ± 0.12 (0.92 ± 0.22) | −0.13 ± 0.16 (1.37 ± 0.05) | 1.92 ± 0.14 (1.57 ± 0.09) | 0.69 ± 0.08 (0.61 ± 0.06) | NA 8 (−0.05 ± 0.05) | Ni | ||||||
| h | A35H T39H (helix) |
0.30 ± 0.01 | 0.48 ± 0.11 (0.33 ± 0.20) | −0.38 ± 0.65 (1.32 ± 0.05) | 2.14 ± 0.12 (1.78 ± 0.13) | 0.71 ± 0.06 (0.73 ± 0.08) | ND 7 | Zn | |||
| 1.75 ± 0.07 (2.01 ± 0.16) | 0.28 ± 0.08 (1.32 ± 0.05) | 2.14 ± 0.12 (1.98 ± 0.06) | 0.71 ± 0.06 (0.75 ± 0.04) | NA 8 (0.02 ± 0.004) | Ni |
Units are kcal · mol−1 (free energies) or kcal · mol−1 ·M−1 (m values). NA, not applicable. ND, not determined.
is the metal-induced stabilization determined by 280nm fluorescence versus GdmCl concentration curve from equilibrium denaturation measurement unless mentioned otherwise. is the metal-induced stabilization obtained from the simultaneous fit of double chevrons. To minimize extrapolation errors, changes in stabilities were calculated at 0.5 and 4.5M GdmCl, and are obtained by simultaneously fitting two chevrons in the absence and presence of 1 mM metal ion, with the parameter of interest being one of the fitting parameters.
and are the ψ0values obtained from double chevron analysis and the fit of a Leffler plot, respectively.
is determined by where ΔCm is the metal-induced change in mid-point, which is the GdmCl concentration where the folded and unfolded populations are the same. is the m0 obtained in the absence of metal ion.
is determined by equilibrium denaturation using circular dichroism measurements at λ = 222nm instead of florescence measurement. The m0 value was shared when equilibrium denaturation data in the absence and presence of metal ion were fitted simultaneously.
The slope of unfolding arm mu was shared when two chevrons were simultaneously fitted.
Chevron shifts vertically upon addition of metal ion. The metal-induced stabilization is too small to provide a well-defined value.
Unfolding arm has two phases of which the fast and slow phase exchange their relative amplitudes as the nickel ion concentration increases while the rates themselves are constant over nickel ion concentration. The ψ0 value could not be obtained from the Leffler plot because ΔΔGeq cannot be determined at the intermediate nickel ion concentration where the relative amplitude of the two phases is poorly determined.
However, the folding behavior for sites e & f and c & d on the carboxy hairpin and between the two hairpins, respectively, were indicative of a non-native arrangement of the strands. The equilibrium stability for the site e and f variants decreased and remained unchanged, respectively. Relaxation rates were Zn2+ dependent for both positions. This unusual behavior indicated that the metal ion binding affinity in the native state was weaker than or comparable to that in the unfolded state. The relative binding affinities were KTSE/KN =0.48±0.07 and 0.95±0.23 for sites e and f, respectively. The stronger metal ion binding affinity in the unfolded state for site e, which is positioned closer to the turn, can be explained by the presence of structure in the denatured state having a biHis arrangement that binds zinc ions stronger than the biHis site in the native state.
The folding rate of site e, and to a much smaller degree, the unfolding rate were decelerated upon addition of zinc ions. The resulting ψ was near unity, , indicating that the carboxy-terminal hairpin is formed in the TSE.
Site f, located at the distal end of the carboxy hairpin, presented folding and unfolding rates that were equally accelerated upon addition of zinc ions (Fig. 2). The metal ion binding affinity in the TSE was 2.6-fold stronger than in the native or unfolded state. The denaturant chevron was shifted upward with the vertex at the same GdmCl concentration. Hence, only the relative barrier height decreased upon addition of metal ions, while the relative depth of the unfolded and native state wells on either side remained unchanged.
ψ0 itself was ill-determined because the change in equilibrium stability was near zero. Nevertheless, the stronger metal ion binding affinity in the TSE than in either the U or N states indicated that in the TSE, the two histidines formed a binding site with a preferred orientation or distance. Hence, the carboxy-terminal hairpin also was present in the TSE.
Upon addition of metal ions for sites c and d that connect the two hairpins, the activation energy for folding was affected more than the equilibrium stability (Fig. 2). Consequently, ψ0 greatly exceeded unity, with and 3.33 ± 0.40 for sites c and d, respectively. The metal ion binding affinities in the TSE were 1.5-fold and 3-fold tighter than in the native state, respectively. Hence, the two hairpins were in close proximity in the TSE, but the two histidines resided in a configuration where they could bind metal ions tighter than the native orientation. We reiterate that because ψ0 was calculated the limit of zero metal ion concentration (e.g., as the single free parameter in a fit to the data in the Leffler plot), the non-native biHis geometry was not induced by the metal binding.
The application of ψ analysis to the helical sites g and h indicated that the helix was largely absent in the TSE, consistent with deductions from φ analysis6; 7. Ni2+ titration only affected the unfolding chevron arm, and vanished for both sites (Fig. 2). Titrating the site g variant with Zn2+ ions yielded . The origin of the minor difference between the ψ values obtained with the two metals ions for site g was unclear. The greater change in stability with Ni2+ (the chevron plot shifted farther to the right) suggested that the Ni2+ data were more reliable.
For the site h variant in Zn2+, both the folding and unfolding rates mildly decreased, and the change in stability was near zero, ΔΔGeq = 0.33±0.20 kcal mol−1. This unexpected downward shift in the chevron plot rendered the ill-determined. Although the Ni2+ data implied the lack of the helix in the TSE, the Zn2+ data for the site h variant indicated that the TSE bound metal ions more weakly than either the unfolded or folded states, e.g., KTSE/KN = 1.99±0.71. Potentially, this part of the chain adopted a non-helical arrangement in the TSE with an extended backbone geometry in which the histidines were located farther apart and with weaker ion binding affinity than in either the unfolded state (where transient helix formation could occur) and the native state (which is helical).
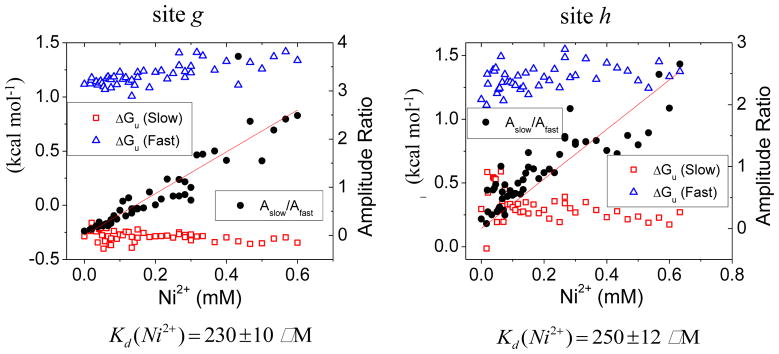
The kinetics of the two helical sites g and h yielded biphasic unfolding traces in Ni2+, with one phase being ~10-fold slower (Fig. 3). Both rates depended on the GdmCl concentration, with the same slope as the unfolding arm of the chevron plots observed for Protein L. The amplitudes of the fast and slow phases, however, depended on metal ion concentration. The faster unfolding rate matched the unfolding rate in the absence of metal ions, while the amplitude of the slower phase increased with the nickel ion concentration.
Fig. 3. Unfolding rates and amplitude dependence on metal concentration for helical sites g and h.
Red line is a fit to the ratio of the two amplitudes [Afast]/[Aslow]= [Me2+]/Kd.
This behavior suggested that the metal ion binding equilibrium at low metal concentration was established slower than the unfolding time constant. The amplitudes of the slower and faster unfolding phases represented the fractions of the metal ion-bound and ion-unbound populations, respectively, present at the initiation of the unfolding reaction. Their relative populations reflected the ion binding affinity in the native state, [bound]/[unbound]=[Me2+]/KN. Regardless, the 10-fold slower unfolding rate for the metal ion bound form was consistent with the loss of helical structure in the route from the native to the TSE.
Hairpin simulations and TSE modeling
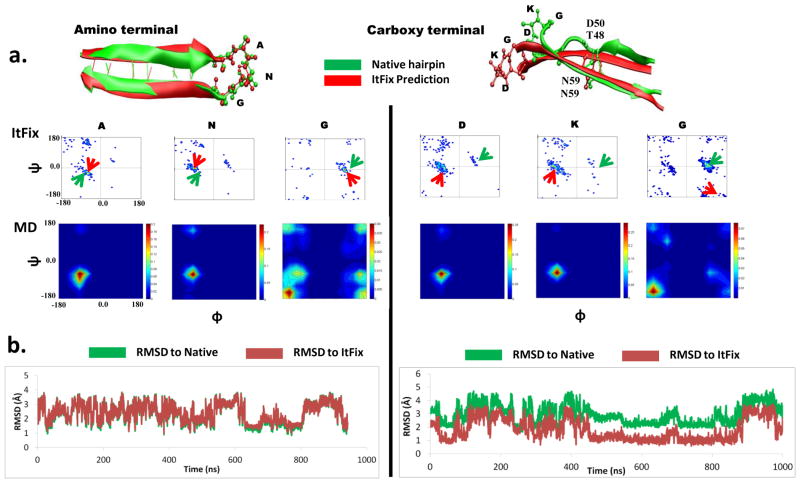
To gain further insight into the non-native ψ values, we conducted simulations of the individual hairpins using both our homology-free ItFix folding algorithm 27; 28 and standard, explicit solvent MD simulations. Both methods do not invoke any knowledge of the native state, and they concurred that the carboxy terminal hairpin forms with a non-native turn geometry. This result was a consequence of the native turn having three consecutive residues with positive backbone φ dihedral angles (Fig. 4a).
Fig. 4. Simulations of the β hairpins.
a. ItFix predictions overlaid on the native hairpins. Ramachandran distributions during the simulations displayed for both ItFix and all-atom MD simulations. The native (green arrow) and predicted (red arrow) torsional angles are depicted. (b) The RMSDs of the six turn residues in the MD simulations to the native and to the ItFix predicted turns.
The ItFix Monte Carlo simulated annealing (MCSA) simulations represent each side chain with a single Cβ atom. The conformational search space is restricted by iteratively fixing 2° structure assignments of certain portions of the sequence after incorporating the influence of 3° context, thereby coupling secondary and tertiary structure determinations. This rapid algorithm can generate accurate predictions of both secondary and tertiary structures without relying on known structures, templates, or fragments27; 28. The method has been validated in CASP8 & CASP9 and was ranked as one of the best groups in the CASP9 refinement category that involves improving template-based models so that they can function as molecular replacement models to solve the phase problem for crystallographic structure determination30.
The ItFix move set involves changes only in a single residue’s φ, ψ backbone dihedral angles (i.e., not a fragment insertion method). The dihedral angles are derived from a PDB-based coil library lacking helices and sheets, and the angles depend on the amino acid type of the residue and each flanking residue. The energy function is the sum of our orientational-dependent DOPE-PW statistical potential28 plus a burial term based on the number of heavy atoms in an 11 Å hemisphere in the direction of the Cα-Cβ vector for each amino acid type31.
Energy minimization in each successive round proceeds with an energy function that also includes the distance constraints derived from the average residue-residue contact and hydrogen bond maps of the structures with the 25% lowest energies from the previous round. Hence, information concerning both 2° and 3° structure learned in prior rounds is carried over to the next round. This iterative fixing protocol mimics the sequential stabilization process observed in the folding of real proteins wherein steps represent the building of new portions on top of existing structures 20; 32.
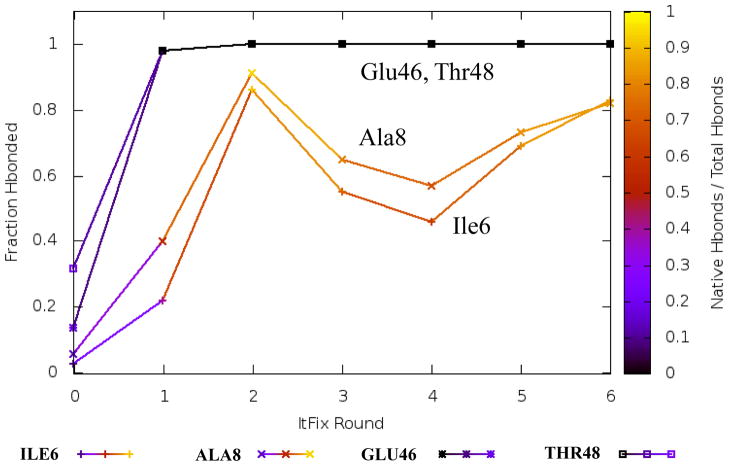
The ItFix algorithm predicted that the amino hairpin adopts a near-native conformation (Figs. 4,5). However, the carboxy hairpin folded into a non-native hairpin with a two-residue registry shift in the hydrogen bonding partners. This hairpin folded in a single ItFix round, with 98% of the structures containing hydrogen bonds between the three non-native residues. In contrast, the amino terminal hairpin required two rounds of folding to obtain a native hairpin conformation. After the first and second rounds, 19% and 81% of the native hydrogen bonds were formed, respectively. Both predicted hairpins were Type 1 β turns, which have dihedral angles that correspond to the dominant dihedral angles in the PBD-based sampling library. The non-native character of the carboxy hairpin emerged because the native φ angles are positive and unfavorable for turn residues D53 and K54, and thus wer only infrequently sampled during the ItFix simulations.
Over the course of the microsecond all-atom MD simulations, both hairpins sampled a variety of conformations, with an RMSD from the native state for the six turn residues fluctuating between 1–5 Å (Fig. 4b). However, the amino hairpin had similar RMSDs to the native and the ItFix-predicted turns, consistent with their joint RMSD being only 1 Å. Further, the MD simulation found the amino turn within 1 Å of the native turn for about 20% of the trajectory. In contrast, the RMSD of the carboxy hairpin to the native turn remained above 2 Å. For half of the MD trajectory, the RMSD relative to the ItFix prediction was closer, ~1 Å. Moreover, the dihedral angles of the turn residues from the MD simulation lie in the same basins as the ItFix predictions. In summary, both computational methods were consistent with the experimental findings of a native-like geometry for the amino hairpin but a non-native geometry for the carboxy hairpin.
Models of the TSE were generated using the ItFix algorithm by docking the native-like amino terminal hairpin against the non-native carboxy hairpin (Fig. 6). Docking was achieved by introducing an additional interaction term between the terminal strands and employing single φi,ψi pivot moves of the unstructured residues between the two hairpins. Ten such structures were selected and further refined in a second MCSA round using our “double crank” local move set that features compensating ψi-1,φi counter-rotations of the neighboring residues31; 33 (Fig. 1).
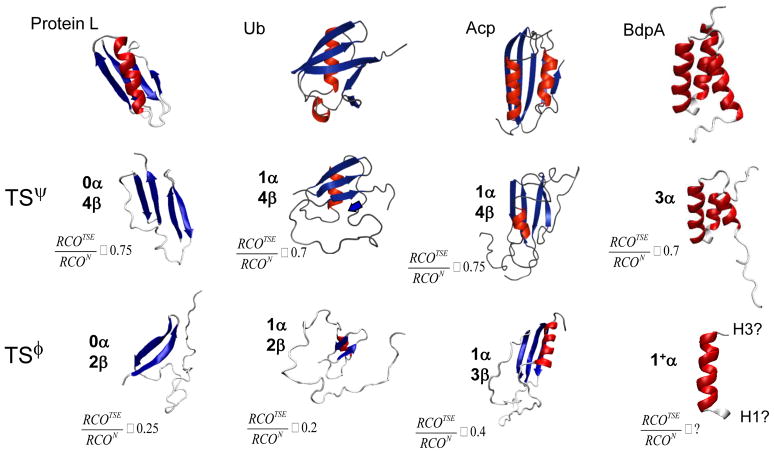
Fig. 6. TSEs determined by ψ analysis are more ordered than those identified by φ analysis.
Although the φ-determined TSE depicted for Acp includes three β strands, only the presence of a hydrophobic core is indicated, and the presence of native-like strand-strand interactions is indeterminate52. Further, the model shown accounts for the remeasured near-zero φ value on F94 that indicates that β5 is absent in Acp’s TSE1. For BdpA, the level of the participation of helices H1 and H3 in the TSE is unclear according to φ analysis63; the model depicted reflects a combination of data from ψ & φ analysis and H/D kinetic isotope effects3.
A considerable extent of Protein L’s native state topology is formed in these TSE models. After insertion of side chains using SCWRL34, their RCO is 73±5% of the native value. The fraction of buried surface in the TSE models, relative to the native state and normalized to an unfolded state ensemble35, is close to the fraction of hydrogen bonds formed in the TSE, approximately 55% and 50%, respectively.
Discussion
The present study is motivated by the belief that a TSE for Protein L containing only a single hairpin, as suggested by φ analysis4; 5; 6; 7, is unreasonably small because it scarcely defines the protein’s topology or has enough hydrogen bonded structure to be commensurate with the observed degree of surface burial. We have applied ψ analysis and demonstrated that the TSE is extensive, containing the entire β sheet network along with some non-native structure associated with the carboxy hairpin. According to our simulations, this hairpin adopts a non-native registry by virtue of the highly unfavorable dihedral angles in the native turn. The same non-native registry is observed both the PDB-based backbone sampling ItFix algorithm and the all-atom simulations. These two methods also concur on the native-like geometry of the amino hairpin, consistent with the experimental ψ data.
These findings have extensive implications concerning the role of non-native structure, the relationship between TSE topology and folding rates, the malleability and multiplicity of TSs, and whether mutational φ analysis, which has been the primary method for comparing experiment and theory, is sufficiently reliable that agreement between the two is an adequate validation of both approaches.
We observe six values of ψ0 equal to unity or larger for biHis sites extending across the four β strands and two near zero ψ0 values on the helical sites. This pattern indicates that the TSE contains the entire β sheet network but minimal helical structure. The ψ0 values greatly exceed unity for sites situated across strands β1–β4 and β3–β4 (ψ0site d = 3.3 ± 0.4 and ψ0site f ≫ 1), a behavior indicating that in the TS, the biHis site has a geometry with tighter metal ion affinity than the site experiences in the native state. Taking further advantage of ψ analysis’ ability to individually determine the metal ion binding affinities in the unfolded, transition and native states, we identified the presence of residual structure in the denatured state for the turn region of the carboxy terminal hairpin. We emphasize that ψ0 is the limiting ψ value in the absence of metal ions. Therefore, these properties are intrinsic to the folding behavior of Protein L and are not artifacts induced by metal ion binding.
The absence of the large helix in the TSE is attributable to its sequence having a low average intrinsic helicity, <2% 36. In addition, all three hydrophobic residues on the buried helical face, which docks against the β sheet, are alanines rather than larger hydrophobic residues. The alanines’ low hydrophobicity reduces the driving force for helix-sheet association.
Evidence that the amino acid sequence, rather than topology, can control the structure of the TSE has been found in experimental φ analysis and computational studies comparing the folding behavior of Protein L and Protein G, two proteins with the same α/β fold4; 5; 6; 7; 8; 9; 10; 11; 12; 13; 14; 15; 16; 17. The possibility of different sequences having alternative TSEs with one hairpin or the other formed implies that a hybrid sequence could fold with significant flux going through two structurally disjoint TSE. However, our present finding that Protein L’s TSE contains both hairpins currently precludes using the Protein L/Protein G comparison as evidence either for sequence altering the TSE structure or for the possibility of structurally disjoint TSEs.
Our ψ-based models of the TSE (Fig. 6) are parsimonious with prior data. The fraction of the surface buried in the TSE models is close to the fraction of hydrogen bonds formed in the TSE. These findings are consistent with kinetic isotope studies that indicate the presence of a commensurate level of surface burial and hydrogen bond formation in the TSE24; 25. The underlying principle is that hydrophobic association leads to partial backbone desolvation that can be offset by protein-protein hydrogen bonding.
A considerable extent of Protein L’s topology is formed in the TSE. Our TSE models have RCOTSE ≈ 0.7·RCON, in agreement with our prior ψ studies for ubiquitin20; 22, acyl phosphatase3; 21 and the B domain of Protein A3. Because these four proteins have native RCO values that span the range observed for two state proteins, the 70% value is likely to be generalizable to other proteins that obey the well known RCO-kf trend18.
Similar relationships emerge from other studies37 with certain G3-based models producing a CO at the 60–80% level38; 39. However, their TSE structures generally correspond to a uniformly “expanded version” of the native structure38, a finding that is inconsistent with ψ data (many ψ values are either zero or near unity). The use of data from φ analysis produces a RCOTSE fraction closer to 50%40, supporting the contention that φ analysis can underreport the structural content of the TSE.
The φ values predicted by Gō models exhibit mixed agreement with experimental φ values for Protein L8 and some other proteins41; 42; 43; 44; 45. The TSE structures for Protein L from the Gō models typically contain just the amino hairpin and the helix 8; 9; 10; 12; 13; 14, but none correctly reproduces the ψ-determined TSE containing only the four strands. The closer agreement between the Gō models and φ analysis may partially be a consequence of their shared native-like biases.
The inability of the Gō-type simulations to correctly predict the four stands in the TSE of Protein L is likely due to both the presence of non-native interactions and the inherent difficulty of correctly balancing the energies associated with different sets of contacts and backbone geometries. Small errors in the energy function, or the lack of explicit hydrogen bonds and backbone φ,ψ dihedral angles can greatly impact the order in which structure forms and the location of the TSE on the reaction surface. These issues contribute to the inability of nearly all methods to accurately describe the TSE structure of a Protein L, as well as of the B domain of Protein A3.
Comparison to φ analysis
Mutational φ analysis is the most accepted method for characterizing TSEs, developing models for folding, and validating theoretical approaches 8; 41; 42; 43; 45. However, the present ψ analysis findings of an extensive TSE in Protein L significantly differ with that generated based on φ analysis. The φ analysis method indicates that Protein L’s TSE contains only the amino hairpin 4; 5; 6; 7; 16 (Fig 1). Seven sites on this hairpin yield φ > 0.6 (although another five positions have φ below 0.31). Six positions on the carboxy terminal hairpin produce much lower average φ of 0.13, while the values at two other positions are slightly higher, φT48A = 0.26 and φV49A = 0.31. Similarly low φ are found on the helical sites.
The primary differences between ψ and φ analyses arise because the former directly probes residue-residue contacts between two known partners, whereas the latter reflects energetic perturbations upon mutation. These perturbations may be the consequence of a combination of factors, including changes in the local side chain environment and backbone dihedral propensities. In ψ analysis, the binding of increasing concentrations of ions to the biHis site produces a nearly continuous increase in the stability of TSE structures that contain the binding site. Hence, the stability is perturbed, yet accomplished in an isosteric and isochemical manner. The resulting series of data can be justifiably combined, and the ψ0 value can be extracted as devoid of any perturbation due to ion binding. The ability of eliminating the influence of perturbations may be inaccessible to traditional mutation studies where the perturbation can arise from multiple sources, including changes in backbone propensities as well as indeterminate non-local interactions.
These differences become critical for Protein L for two reasons, the non-native character of the carboxy hairpin and the exposure of the β sheet’s hydrophobic face in the TSE. The two amino acid register shift in the carboxy hairpin indicated by the simulations results in non-native contacts along this hairpin and non-native dihedral angles in the turn. Consequently, the energetic perturbation realized in the TSE likely is smaller than in the less accommodating native state, and φ therefore becomes small and mistakenly identifies this hairpin as being absent in the TSE.
The second issue arises because the otherwise buried side chains on the hydrophobic face of the sheet are solvent exposed in the TSE due to the absence of the helix. Consequently, the energetic penalty for the truncation of the side chain for the residues on the inner face of hairpins, for example, imparted by an alanine substitution, is diminished in the TSE relative to the native state, even though the residue is in a hydrogen bonded β structure. This analysis provides an explanation for the low to moderate φ values for the native-like amino hairpin 4; 5; 6; 7; 16. The issue is generally relevant whenever φ analysis is applied at any position that is more exposed in the TSE than in the native state.
Overall, these considerations support the contention that φ analysis can underestimate or misrepresent the structural content of the TSE 2; 20; 26; 29; 46 due to chain relaxation and accommodation or to non-native interactions 47; 48. For example, a residue in fyn SH3 with a helical conformation in the native state adopts a β conformation in the TSE despite having a high canonical φ value of 0.749. A similarly positioned residue in src SH3 also contains a productive non-native conformation in the TSE50. Likewise, in non-native regions of the cytochrome b562 intermediate, seven high φ values are observed (0.4≤φ≤1.0)48. Conversely, low φ values are found in regions of native-like structure in BPTI intermediates46.
In addition to Protein L, significant underreporting of the TSE’s structural content by φ analysis also occurs with acyl phosphatase1; 51; 52, ubiquitin2; 29 and the B domain of Protein A3 (Fig. 6). The ψ-determined TSEs for these proteins are extensive and contain persistent native-like tertiary interactions. Unambiguous sites where ψ is unity indicate that the TSEs of acyl phosphatase and ubiquitin contain a four-stranded β sheet and an α helix. For these two α/β proteins, ψ analysis detects the presence of one and two additional long-range β strands than φ analysis identifies, respectively. We suspect underreporting occurs with proteins having a TSE characterized by φ analysis as polarized, such as cold shock protein53, src SH354 and Protein G15.
Conclusion
We demonstrate that the highly studied TSE state of Protein L is extensive and has non-native properties that likely arise due to the presence in the native state of backbone dihedral angles that are not highly populated at the earliest stage of folding. The TSE is significantly larger than the one identified by φ analysis, a result found in the three other proteins probed by ψ analysis (Fig. 6). The difference arises because ψ directly identifies inter-residue contacts between known partners, while φ is native-centric and the TSE can be less sensitive to energetic perturbations than the native state even for structured regions. These observations suggest that identification of a TSE as being diffuse, polarized or an expanded version of the native state based on φ analysis alone should be reconsidered.
Our results also emphasize that apparent agreement between the φ values and Gō-based models45 can produce an overly optimistic view of these methods’ ability to accurately determine TSE structures. Accurate modeling of protein folding remains an ongoing challenge, requiring the proper balancing of numerous factors in a changing contextual environment as the chain folds. ψ analysis should be applied to other proteins to address these outstanding issues, search for other non-native TSE structures, and provide a robust test set for benchmarking simulation, which may lead to better agreement between theory and experiment.
Materials and Methods
Folding measurements
The pseudo wild-type sequence used has 64 amino acids, MEEVTIKANL IFANGSTQTA EFKGTFEKAT SEAYAYADTL KKDNGEWTVD VADKGYTLNI KFAG, which contains a Y47W mutation to enable fluorescence monitored folding and unfolding. All variants are verified by DNA sequencing prior to expression. Purification uses either reverse-phase HPLC (C8 and C18 columns), or ion-exchange (Amersham Biosciences Q Sepharose® Fast Flow) followed by gel filtration HPLC (GE Healthcare HiPrep™ 16/60 Sephacryl™ S-100) in series. Protein samples are extracted in powder form following lyophilization. The purity of some mutants is verified by mass spectroscopy.
All measurements are taken in 100 mM NaCl, 50 mM Tris·HCl or HEPES, pH 7.5 buffer at 22 °C. Equilibrium folded and unfolded populations are measured via changes in circular dichroism using a Jasco 715 spectropolarimeter with a 1-cm path length. Kinetic data are collected using a Biologic SFM-400 stopped-flow apparatus and a PTI A101 arc lamp. Fluorescence spectroscopy uses λexcite=285 nm, and emission is observed at λ =310–400 nm. Stock metal solutions of 250 mM ZnCl2 and NiCl2 are individually prepared in 10 mM HCl, as a concentrated source of metal cations, and are diluted to desired concentration prior to every experiment.
Data analysis
The kinetic data are analyzed using the “chevron analysis” of the denaturant dependence of folding rate constants 55 where ΔGf, ΔGu, and ΔGeq are linearly dependent on denaturant concentration
| (4a) |
| (4b) |
| (4c) |
where R is the universal gas constant, T is the temperature. The dependence on denaturant concentration [den], the m-values, report on the degree of surface area burial during the folding process. The equilibrium values can be calculated from the kinetic measurements according to ΔGeq ([Me2+]) = ΔGf ([Me2+]) − ΔGu ([Me2+]) and mo=mu+mf. To minimize extrapolation errors, ΔGf and ΔGu are calculated for strongly folding and unfolding conditions, respectively. ψ0 values are determined from a simultaneous fit to the zero and high Me2+ chevrons, with ψ0 being one of the fitting parameters and using Eq. 3. Parameters are fit using non-linear least-squares algorithms implemented in the Microcal Origin software package.
All-atom MD simulations
Following similar protocols as in our previous studies 56; 57, we have simulated both the amino and carboxy hairpins of Protein L with all-atom MD simulations, starting with non-native, random coil conformations. The hairpin length is 24 aa and 21 aa for amino terminal hairpin and carboxy hairpin, respectively. The hairpin fragments are solvated in a 54.5 Å × 48.0 Å × 45.0 Å water box, and then sodium ions and chloride ions are added to neutralize and mimic the experimental environment (100 mM NaCl concentration). Both solvated systems contain approximately 12,000 atoms each. The IBM BlueGene-optimized NAMD2 58 package is utilized for the MD simulations with the NPT ensemble at 1 atm and 295 K. The CHARMM (parameter set c32b1) force field is used for the protein 59, and TIP3P water provides the model used as the explicit solvent 60; 61. The Particle Mesh Ewald (PME) method has been applied to treat the long-range electrostatic interactions, and a 12 Å cutoff employed for the van der Waals interactions. The systems is first minimized and then followed by a 500,000 step equilibration. A snapshot taken during the equilibration is randomly selected as the starting point for the subsequent micro-seconds production runs. The time step for the production runs is 2 fs, and the SHAKE/RATTLE algorithm is applied 62. The aggregate MD simulation time exceeds 4 μs.
Fig. 5. Rate of β hairpin formation.
The carboxy terminal hairpin forms in fewer rounds than the amino terminal hairpin. The carboxy hairpin folds in a single round, with 98% of the structures containing hydrogen bonds between the three non-native amino acid partners. In contrast, the amino terminal hairpin requires two rounds of folding to obtain a native hairpin conformation. After the first and second rounds, 19% and 81% of the native hydrogen bonds are formed, respectively. The y-axis presents the fraction of the maximum number of hydrogen bonds for the hairpins. The color intensity reflects the native character (0=non-native, 1= all native).
Acknowledgments
We thank members of the Freed and Sosnick groups for helpful discussions, and C. Antoniou for assistance in protein production. This work was supported, in part, by NIH grant GM55694 (TRS), NSF Grant CHE-1111918 (KF) and The University of Chicago-Argonne National Laboratory Seed Grant Program (TRS, Mike Wilde).
Abbreviations
- biHis
bi-histidine
- GdmCl
guanidinium chloride
- KD, KN, KTSE
metal ion binding affinity of denatured, native and transition states, respectively
- MD
molecular dynamics
- MCSA
Monte Carlo simulated annealing
- Protein L
62 residue α/β IgG binding domain of protein L
- RCO
relative contact order
- TSE
transition state ensemble
- ΔΔGeq
change in equilibrium stability
- ΔΔGf and ΔΔGu
change in folding and unfolding activation free energy
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Pandit AD, Jha A, Freed KF, Sosnick TR. Small Proteins Fold Through Transition States With Native-like Topologies. J Mol Biol. 2006;361:755–70. doi: 10.1016/j.jmb.2006.06.041. [DOI] [PubMed] [Google Scholar]
- 2.Sosnick TR, Dothager RS, Krantz BA. Differences in the folding transition state of ubiquitin indicated by phi and psi analyses. Proc Natl Acad Sci U S A. 2004;101:17377–82. doi: 10.1073/pnas.0407683101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Baxa M, Freed KF, Sosnick TR. Quantifying the Structural Requirements of the Folding Transition State of Protein A and Other Systems. J Mol Biol. 2008;381:1362–1381. doi: 10.1016/j.jmb.2008.06.067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Scalley ML, Yi Q, Gu H, McCormack A, Yates JR, 3rd, Baker D. Kinetics of folding of the IgG binding domain of peptostreptococcal protein L. Biochemistry. 1997;36:3373–82. doi: 10.1021/bi9625758. [DOI] [PubMed] [Google Scholar]
- 5.Gu H, Kim D, Baker D. Contrasting roles for symmetrically disposed beta-turns in the folding of a small protein. J Mol Biol. 1997;274:588–96. doi: 10.1006/jmbi.1997.1374. [DOI] [PubMed] [Google Scholar]
- 6.Kim DE, Yi Q, Gladwin ST, Goldberg JM, Baker D. The single helix in protein L is largely disrupted at the rate-limiting step in folding. J Mol Biol. 1998;284:807–15. doi: 10.1006/jmbi.1998.2200. [DOI] [PubMed] [Google Scholar]
- 7.Kim DE, Fisher C, Baker D. A Breakdown of Symmetry in the Folding Transition State of Protein L. J Mol Biol. 2000;298:971–984. doi: 10.1006/jmbi.2000.3701. [DOI] [PubMed] [Google Scholar]
- 8.Clementi C, Garcia AE, Onuchic JN. Interplay among tertiary contacts, secondary structure formation and side-chain packing in the protein folding mechanism: all-atom representation study of protein L. J Mol Biol. 2003;326:933–54. doi: 10.1016/s0022-2836(02)01379-7. [DOI] [PubMed] [Google Scholar]
- 9.Karanicolas J, Brooks CL., 3rd The origins of asymmetry in the folding transition states of protein L and protein G. Protein Sci. 2002;11:2351–61. doi: 10.1110/ps.0205402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Brown S, Head-Gordon T. Intermediates and the folding of proteins L and G. Protein Sci. 2004;13:958–70. doi: 10.1110/ps.03316004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Yang Q, Sze SH. Predicting protein folding pathways at the mesoscopic level based on native interactions between secondary structure elements. BMC bioinformatics. 2008;9:320. doi: 10.1186/1471-2105-9-320. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Zhao L, Wang J, Dou X, Cao Z. Studying the unfolding process of protein G and protein L under physical property space. BMC bioinformatics. 2009;10(Suppl 1):S44. doi: 10.1186/1471-2105-10-S1-S44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Ejtehadi MR, Avall SP, Plotkin SS. Three-body interactions improve the prediction of rate and mechanism in protein folding models. Proc Natl Acad Sci U S A. 2004;101:15088–93. doi: 10.1073/pnas.0403486101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Koga N, Takada S. Roles of native topology and chain-length scaling in protein folding: a simulation study with a Go-like model. J Mol Biol. 2001;313:171–80. doi: 10.1006/jmbi.2001.5037. [DOI] [PubMed] [Google Scholar]
- 15.McCallister EL, Alm E, Baker D. Critical role of beta-hairpin formation in protein G folding. Nature Struct Biol. 2000;7:669–673. doi: 10.1038/77971. [DOI] [PubMed] [Google Scholar]
- 16.Nauli S, Kuhlman B, Baker D. Computer-based redesign of a protein folding pathway. Nature Struct Biol. 2001;8:602–605. doi: 10.1038/89638. [DOI] [PubMed] [Google Scholar]
- 17.Kuhlman B, O’Neill JW, Kim DE, Zhang KY, Baker D. Accurate computer-based design of a new backbone conformation in the second turn of protein L. J Mol Biol. 2002;315:471–7. doi: 10.1006/jmbi.2001.5229. [DOI] [PubMed] [Google Scholar]
- 18.Plaxco KW, Simons KT, Baker D. Contact order, transition state placement and the refolding rates of single domain proteins. J Mol Biol. 1998;277:985–994. doi: 10.1006/jmbi.1998.1645. [DOI] [PubMed] [Google Scholar]
- 19.Plaxco KW, Simons KT, Ruczinski I, Baker D. Topology, stability, sequence, and length: defining the determinants of two-state protein folding kinetics. Biochemistry. 2000;39:11177–11183. doi: 10.1021/bi000200n. [DOI] [PubMed] [Google Scholar]
- 20.Krantz BA, Dothager RS, Sosnick TR. Discerning the structure and energy of multiple transition states in protein folding using psi-analysis. J Mol Biol. 2004;337:463–75. doi: 10.1016/j.jmb.2004.01.018. [DOI] [PubMed] [Google Scholar]
- 21.Pandit AD, Krantz BA, Dothager RS, Sosnick TR. Characterizing protein folding transition states using Psi-analysis. Methods Mol Biol. 2007;350:83–104. doi: 10.1385/1-59745-189-4:83. [DOI] [PubMed] [Google Scholar]
- 22.Sosnick TR, Krantz BA, Dothager RS, Baxa M. Characterizing the Protein Folding Transition State Using psi Analysis. Chem Rev. 2006;106:1862–76. doi: 10.1021/cr040431q. [DOI] [PubMed] [Google Scholar]
- 23.Sosnick TR. Kinetic barriers and the role of topology in protein and RNA folding. Protein Sci. 2008;17:1308–1318. doi: 10.1110/ps.036319.108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Krantz BA, Srivastava AK, Nauli S, Baker D, Sauer RT, Sosnick TR. Understanding protein hydrogen bond formation with kinetic H/D amide isotope effects. Nature Struct Biol. 2002;9:458–63. doi: 10.1038/nsb794. [DOI] [PubMed] [Google Scholar]
- 25.Krantz BA, Moran LB, Kentsis A, Sosnick TR. D/H amide kinetic isotope effects reveal when hydrogen bonds form during protein folding. Nature Struct Biol. 2000;7:62–71. doi: 10.1038/71265. [DOI] [PubMed] [Google Scholar]
- 26.Krantz BA, Sosnick TR. Engineered metal binding sites map the heterogeneous folding landscape of a coiled coil. Nature Struct Biol. 2001;8:1042–1047. doi: 10.1038/nsb723. [DOI] [PubMed] [Google Scholar]
- 27.DeBartolo J, Hocky G, Wilde M, Xu J, Freed KF, Sosnick TR. Protein structure prediction enhanced with evolutionary diversity: SPEED. Protein Sci. 2010;19:520–34. doi: 10.1002/pro.330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.DeBartolo J, Colubri A, Jha AK, Fitzgerald JE, Freed KF, Sosnick TR. Mimicking the folding pathway to improve homology-free protein structure prediction. Proc Natl Acad Sci U S A. 2009;106:3734–9. doi: 10.1073/pnas.0811363106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Baxa MC, Freed KF, Sosnick TR. Psi-constrained simulations of protein folding transition states: implications for calculating Phi values. J Mol Biol. 2009;386:920–8. doi: 10.1016/j.jmb.2009.01.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Adhikari AN, Peng J, Wilde M, Xu J, Freed KF, Sosnick TR. Modeling large regions in proteins: Applications to loops, termini, and folding. Protein Sci. 2012;21:107–21. doi: 10.1002/pro.767. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Adhikari AN, Peng J, Wilde M, Xu J, Freed KF, Sosnick TR. A fragment free approach to ab initio local protein structure prediction. Protein Sci (in press) [Google Scholar]
- 32.Maity H, Maity M, Krishna MM, Mayne L, Englander SW. Protein folding: The stepwise assembly of foldon units. Proc Natl Acad Sci U S A. 2005;102:4741–6. doi: 10.1073/pnas.0501043102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Haddadian EJ, Gong H, Jha AK, Yang X, Debartolo J, Hinshaw JR, Rice PA, Sosnick TR, Freed KF. Automated real-space refinement of protein structures using a realistic backbone move set. Biophys J. 2011;101:899–909. doi: 10.1016/j.bpj.2011.06.063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Krivov GG, Shapovalov MV, Dunbrack RL., Jr Improved prediction of protein side-chain conformations with SCWRL4. Proteins. 2009;77:778–95. doi: 10.1002/prot.22488. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Jha AK, Colubri A, Freed KF, Sosnick TR. Statistical coil model of the unfolded state: Resolving the reconciliation problem. Proc Natl Acad Sci U S A. 2005;102:13099–104. doi: 10.1073/pnas.0506078102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Lacroix E, Viguera AR, Serrano L. Elucidating the folding problem of alpha-helices: local motifs, long-range electrostatics, ionic-strength dependence and prediction of NMR parameters. J Mol Biol. 1998;284:173–91. doi: 10.1006/jmbi.1998.2145. [DOI] [PubMed] [Google Scholar]
- 37.Bai Y, Zhou H, Zhou Y. Critical nucleation size in the folding of small apparently two-state proteins. Protein Sci. 2004;13:1173–81. doi: 10.1110/ps.03587604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Wallin S, Chan HS. Conformational entropic barriers in topology-dependent protein folding: perspectives from a simple native-centric polymer model. J Phys: Condens Matter. 2006;18:S307–S328. [Google Scholar]
- 39.Ferguson A, Liu Z, Chan HS. Desolvation barrier effects are a likely contributor to the remarkable diversity in the folding rates of small proteins. J Mol Biol. 2009;389:619–36. doi: 10.1016/j.jmb.2009.04.011. [DOI] [PubMed] [Google Scholar]
- 40.Paci E, Lindorff-Larsen K, Dobson CM, Karplus M, Vendruscolo M. Transition state contact orders correlate with protein folding rates. J Mol Biol. 2005;352:495–500. doi: 10.1016/j.jmb.2005.06.081. [DOI] [PubMed] [Google Scholar]
- 41.Munoz V, Eaton WA. A simple model for calculating the kinetics of protein folding from three-dimensional structures. Proc Natl Acad Sci U S A. 1999;96:11311–6. doi: 10.1073/pnas.96.20.11311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Shoemaker BA, Wang J, Wolynes PG. Exploring structures in protein folding funnels with free energy functionals: the transition state ensemble. J Mol Biol. 1999;287:675–94. doi: 10.1006/jmbi.1999.2613. [DOI] [PubMed] [Google Scholar]
- 43.Alm E, Baker D. Prediction of protein-folding mechanisms from free-energy landscapes derived from native structures. Proc Natl Acad Sci U S A. 1999;96:11305–10. doi: 10.1073/pnas.96.20.11305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Galzitskaya OV, Finkelstein AV. A theoretical search for folding/unfolding nuclei in three-dimensional protein structures. Proc Natl Acad Sci U S A. 1999;96:11299–304. doi: 10.1073/pnas.96.20.11299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Takada S. Go-ing for the prediction of protein folding mechanisms. Proc Natl Acad Sci U S A. 1999;96:11698–700. doi: 10.1073/pnas.96.21.11698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Bulaj G, Goldenberg DP. Phi-values for BPTI folding intermediates and implications for transition state analysis. Nature Struct Biol. 2001;8:326–330. doi: 10.1038/86200. [DOI] [PubMed] [Google Scholar]
- 47.Neudecker P, Zarrine-Afsar A, Choy WY, Muhandiram DR, Davidson AR, Kay LE. Identification of a Collapsed Intermediate with Non-native Long-range Interactions on the Folding Pathway of a Pair of Fyn SH3 Domain Mutants by NMR Relaxation Dispersion Spectroscopy. J Mol Biol. 2006;363:958–976. doi: 10.1016/j.jmb.2006.08.047. [DOI] [PubMed] [Google Scholar]
- 48.Feng H, Vu ND, Zhou Z, Bai Y. Structural examination of Phi-value analysis in protein folding. Biochemistry. 2004;43:14325–31. doi: 10.1021/bi048126m. [DOI] [PubMed] [Google Scholar]
- 49.Zarrine-Afsar A, Dahesh S, Davidson AR. A residue in helical conformation in the native state adopts a beta- strand conformation in the folding transition state despite its high and canonical Phi-value. Proteins. 2012 doi: 10.1002/prot.24030. [DOI] [PubMed] [Google Scholar]
- 50.Di Nardo AA, Korzhnev DM, Stogios PJ, Zarrine-Afsar A, Kay LE, Davidson AR. Dramatic acceleration of protein folding by stabilization of a nonnative backbone conformation. Proc Natl Acad Sci U S A. 2004;101:7954–9. doi: 10.1073/pnas.0400550101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Chiti F, Taddei N, White PM, Bucciantini M, Magherini F, Stefani M, Dobson CM. Mutational analysis of acylphosphatase suggests the importance of topology and contact order in protein folding. Nature Struct Biol. 1999;6:1005–9. doi: 10.1038/14890. [DOI] [PubMed] [Google Scholar]
- 52.Taddei N, Chiti F, Fiaschi T, Bucciantini M, Capanni C, Stefani M, Serrano L, Dobson CM, Ramponi G. Stabilisation of alpha-helices by site-directed mutagenesis reveals the importance of secondary structure in the transition state for acylphosphatase folding. J Mol Biol. 2000;300:633–647. doi: 10.1006/jmbi.2000.3870. [DOI] [PubMed] [Google Scholar]
- 53.Garcia-Mira MM, Boehringer D, Schmid FX. The folding transition state of the cold shock protein is strongly polarized. J Mol Biol. 2004;339:555–69. doi: 10.1016/j.jmb.2004.04.011. [DOI] [PubMed] [Google Scholar]
- 54.Grantcharova VP, Riddle DS, Santiago JV, Baker D. Important role of hydrogen bonds in the structurally polarized transition state for folding of the src SH3 domain. Nature Struct Biol. 1998;5:714–720. doi: 10.1038/1412. [DOI] [PubMed] [Google Scholar]
- 55.Matthews CR. Effects of point mutations on the folding of globular proteins. Methods Enzymol. 1987;154:498–511. doi: 10.1016/0076-6879(87)54092-7. [DOI] [PubMed] [Google Scholar]
- 56.Das P, King JA, Zhou R. Aggregation of gamma-crystallins associated with human cataracts via domain swapping at the C-terminal beta-strands. Proc Natl Acad Sci USA. 2011;108:10514–9. doi: 10.1073/pnas.1019152108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Zhou R, Berne BJ, Germain R. The free energy landscape for beta hairpin folding in explicit water. Proc Natl Acad Sci USA. 2001;98:14931–6. doi: 10.1073/pnas.201543998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Kumar SHC, Zheng G, Bohm E, Bhatele A, Phillips JC, Yu H, Kale LV. Scalable molecular dynamics with NAMD on the IBM Blue Gene/L system. IBM J Res Dev. 2008;52:177–188. [Google Scholar]
- 59.Brooks BR, Brooks CL, 3rd, Mackerell AD, Jr, Nilsson L, Petrella RJ, Roux B, Won Y, Archontis G, Bartels C, Boresch S, Caflisch A, Caves L, Cui Q, Dinner AR, Feig M, Fischer S, Gao J, Hodoscek M, Im W, Kuczera K, Lazaridis T, Ma J, Ovchinnikov V, Paci E, Pastor RW, Post CB, Pu JZ, Schaefer M, Tidor B, Venable RM, Woodcock HL, Wu X, Yang W, York DM, Karplus M. CHARMM: the biomolecular simulation program. J Comp Chem. 2009;30:1545–614. doi: 10.1002/jcc.21287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML. Comparison of simple potential functions for simulating liquid water. J Comp Chem. 1983;79:926–935. [Google Scholar]
- 61.Neria E, Karplus M. A position dependent friction model for solution reactions in the high friction regime: Proton transfer in triosephosphate isomerase (TIM) J Chem Phys. 1996;105:10812–10818. [Google Scholar]
- 62.Ryckaert JP, CG, Berendsen HJC. Numerical integration of the cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes. J Comp Phys. 1977;23:327–341. [Google Scholar]
- 63.Sato S, Fersht AR. Searching for multiple folding pathways of a nearly symmetrical protein: temperature dependent phi-value analysis of the B domain of protein A. J Mol Biol. 2007;372:254–67. doi: 10.1016/j.jmb.2007.06.043. [DOI] [PubMed] [Google Scholar]