Population pharmacokinetics and maximum a posteriori probability Bayesian estimator of abacavir: application of individualized therapy in HIV-infected infants and toddlers

Abstract

AIMS

To develop a population pharmacokinetic model for abacavir in HIV-infected infants and toddlers, which will be used to describe both once and twice daily pharmacokinetic profiles, identify covariates that explain variability and propose optimal time points to optimize the area under the concentration–time curve (AUC) targeted dosage and individualize therapy.

METHODS

The pharmacokinetics of abacavir was described with plasma concentrations from 23 patients using nonlinear mixed-effects modelling (NONMEM) software. A two-compartment model with first-order absorption and elimination was developed. The final model was validated using bootstrap, visual predictive check and normalized prediction distribution errors. The Bayesian estimator was validated using the cross-validation and simulation–estimation method.

RESULTS

The typical population pharmacokinetic parameters and relative standard errors (RSE) were apparent systemic clearance (CL) 13.4 l h⁻¹ (RSE 6.3%), apparent central volume of distribution 4.94 l (RSE 28.7%), apparent peripheral volume of distribution 8.12 l (RSE14.2%), apparent intercompartment clearance 1.25 l h⁻¹ (RSE 16.9%) and absorption rate constant 0.758 h⁻¹ (RSE 5.8%). The covariate analysis identified weight as the individual factor influencing the apparent oral clearance: CL = 13.4 × (weight/12)^1.14. The maximum a posteriori probability Bayesian estimator, based on three concentrations measured at 0, 1 or 2, and 3 h after drug intake allowed predicting individual AUC_0–t.

CONCLUSIONS

The population pharmacokinetic model developed for abacavir in HIV-infected infants and toddlers accurately described both once and twice daily pharmacokinetic profiles. The maximum a posteriori probability Bayesian estimator of AUC_0–t was developed from the final model and can be used routinely to optimize individual dosing.

WHAT IS ALREADY KNOWN ABOUT THIS SUBJECT

• Abacavir is used to treat HIV infection in both adults and children. The recommended paediatric dose is 8 mg kg⁻¹ twice daily up to a maximum of 300 mg twice daily.

• Weight was identified as the central covariate influencing pharmacokinetics of abacavir in children.

WHAT THIS STUDY ADDS

• A population pharmacokinetic model was developed to describe both once and twice daily pharmacokinetic profiles of abacavir in infants and toddlers.

• Standard dosage regimen is associated with large interindividual variability in abacavir concentrations.

• A maximum a posteriori probability Bayesian estimator of AUC_0–t based on three time points (0, 1 or 2, and 3 h) is proposed to support area under the concentration–time curve (AUC) targeted individualized therapy in infants and toddlers.

Introduction

Abacavir is a nucleoside reverse transcriptase inhibitor, administered in combination antiretroviral therapy for both paediatric and adult patients with human immunodeficiency (HIV) virus infection [1].

Abacavir is well absorbed following oral administration and is distributed into body tissues, including the central nervous system. It is extensively metabolized by the liver, and less than 2% is excreted as unchanged drug in the urine. The two major catabolic pathways include alcohol dehydrogenase and conjugation by uridine diphosphate glucuronyltransferase (UGT), resulting in inactive carboxylate and glucuronide metabolites [2, 3]. The antiviral activity of abacavir results from its intracellular activation to carbovir triphosphate, which competes with the endogenous nucleotide 2′-deoxyguanosine triphosphate for incorporation into the nucleic acid chain and terminates the DNA chain by preventing addition of new bases [4]. The most common adverse reactions to abacavir are nausea, vomiting, fatigue, headache and diarrhoea. Their frequency drops dramatically with continued treatment. Life-threatening hypersensitivity reactions have also been reported in 2–3% of paediatric patients, usually within the first month of treatment [1, 3].

Abacavir has been licensed for paediatric patients over 3 months of age with the recommended dosage regimen of 8 mg kg⁻¹ (up to a maximum of 300 mg) twice daily. In clinical practice, abacavir therapy was initiated in children with this weight-normalized dosage regimen. Indeed, weight is currently taken as a significant developmental variable. However, there are still challenges for individual patient management, because interindividual pharmacokinetic variability is large. Weight changes may not reflect the impact of additional physiological factors related to developmental growth. Therefore, the standard dose may not be suitable for all the infants and toddlers, whatever their age, if only adapted to weight.

Therapeutic drug monitoring (TDM) guided individualized antiretroviral therapy aims to measure predefined antiretroviral concentrations in a single patient for the purpose of optimizing the dose to maximize the likelihood of achieving desired therapeutic goals [5]. Numerous papers have suggested children as a target population for antiretrovirals [6–8]. For abacavir, a pharmacokinetic–pharmacodynamic study in adults demonstrated that the endpoint for efficacy, as indicated by the change from baseline in viral load (plasma HIV-1 RNA) and rise in CD4+ T cell count, was significantly correlated with area under the concentration–time curve (AUC) [9]. Given the mechanism of action of abacavir, the exposure–effect relationship can be assumed to be independent of age. The adult AUC_0–12 target value of 6.02 µg h ml⁻¹ can be set as the target exposure for effective and safe treatment in children [10]. These findings provide the rationale for AUC guided abacavir dosing adjustment, but implementation in clinical practice is missing. A full AUC, which involves a minimum of six to eight blood samples over 12 or 24 h, is not a viable option due to practical and cost issues, in particular for young children. The present study was conducted to overcome this problem with the following aims: (i) to develop a population pharmacokinetic model, which will be used to describe pharmacokinetic profiles of both once and twice daily use; and (ii) to propose a maximum a posteriori probability (MAP) Bayesian estimator based on a limited number of samples to predict AUC_0–t and to be used for TDM of abacavir.

Patients and methods

Pharmacokinetic data

The data were obtained from the PENTA 15 study, run by Pediatric European Network for the Treatment of AIDS (PENTA) [11]. Briefly, this open-label, crossover, multicentre study was undertaken to compare once and twice daily dosing of abacavir and lamivudine in HIV type-1-infected children aged 3–36 months. Intensive plasma pharmacokinetic sampling was performed while children were on twice daily abacavir (8 mg kg⁻¹) ± lamivudine (4 mg kg⁻¹), after which children changed to once daily abacavir (16 mg kg⁻¹) ± lamivudine (8 mg kg⁻¹) and pharmacokinetic sampling was repeated 4 weeks later. Abacavir plasma concentrations were measured by high-pressure liquid chromatography with ultraviolet detection at the department of Pediatric Pharmacology and Pharmacogenetics, Hôpital Robert Debré, Paris, France. Analytical methods were cross-validated with the Department of Clinical Pharmacy of the Radboud University Nijmegen Medical Center, The Netherlands, where the assay was developed [11]. The assay was validated over the concentration range of 0.015–5 mg l⁻¹. The average accuracies were 92–102%, inter- and intraday coefficients of variation were <2.5%, extraction recoveries were higher than 97% and the lower limit of quantification (LLQ) was 0.015 mg l⁻¹.

Samples were obtained at steady-state at time T0 (immediately before administration) and T1, T2, T3, T4, T6, T8 and T12 h after administration in the twice daily regimen and an additional sample at T24 h in the once daily regimen. The protocol was approved by the Ethics Committee for each centre participating in the study within PENTA. All parents or guardians provided written informed consent.

Pharmacokinetic analysis

Pharmacokinetic analysis was carried out using the nonlinear mixed-effects modelling program NONMEM VI (V2.0; ICON development solutions, Ellicott City, MD, USA). The first-order conditional estimation method with interaction option was used to estimate pharmacokinetic parameters and their variability.

The model was parameterized in terms of absorption rate constant (K_a), apparent oral clearance (CL/F), apparent central volume of distribution (V₁/F), apparent peripheral volume of distribution (V₂/F) and apparent intercompartment clearance (Q/F).

Interindividual variability of the pharmacokinetic parameters was estimated using an exponential model and could be expressed as follows:

where θ_A is the typical population value of pharmacokinetic parameter, η_j^θA is the difference between the log-transformed individual-specific parameter and the log-transformed typical individual's parameter, and represents the random effect for parameter θ in patient j. The η_j^θA values are independent, identically distributed random variables and normally distributed around 0 with variance ω², and j is the variable for jth individual.

Covariate analysis

The effects of weight, age, height, gender, body mass index, serum creatinine and drug administration frequency were investigated as potential variables on pharmacokinetic parameters. The systematic covariate analysis process [12] and likelihood ratio test was used to test the effect of each variable.

The selection of variables was determined using a forward and backward selection process. During forward selection, a covariate was selected only if a significant (P < 0.05, χ² distribution with one degree of freedom) decrease (reduction > 3.84) in the objective function value (OFV) from the basic model was obtained. Then all the variables found to be significant were added simultaneously into a ‘full’ model. The importance of each variable was re-evaluated by backward selection. Each variable was independently removed from the full model to confirm its relevance. An increase in the OFV of more than 6.635 (P < 0.01, χ² distribution) was required for confirmation. The resulting model was called the ‘final’ population pharmacokinetic model. which included all significant variables.

Model validation

Goodness-of-fit plots, including observed (OBS) vs. individual prediction (IPRED), OBS vs. population prediction (PRED), conditional weighted residuals (CWRES) vs. time and CWRES vs. PRED were used for diagnostic purposes [13].

The stability and performance of the final model were assessed by means of an internal validation method involving a nonparametric bootstrap with resampling and replacement stratified on weight. Resampling was repeated 1000 times, and the values of estimated parameters from the bootstrap procedure were compared with those estimated from the original data set. The entire procedure was performed in an automated fashion, using Perl-speaks-NONMEM [14].

The final model was also assessed by visual predictive check (VPC) and metric normalized prediction distribution errors (NPDE) [15]. One thousand data sets were simulated using the final population model parameters. For VPC, the 50th percentile concentration (as an estimator of the population-predicted concentration) and the 5th and 95th percentile concentrations were processed by R for NONMEM (v.20070911) and then plotted against elapsed time. A suitable model was defined as approximately 90% of data points within the 5th–95th prediction interval (approximately 5% above 95th and 5% below 5th). For NPDEs, the following graphs are plotted by NPDE R package (v1.2): (i) Q-Q (probability) plot of the NPDE; (ii) histogram of the NPDE; (iii) NPDE vs. time; and (iv) NPDE vs. predicted concentrations. The NPDE is expected to follow the normal distribution N(0, 1) [16].

Maximum a posteriori probability Bayesian estimator

From a practical point of view, we stated a priori that the best MAP Bayesian estimator should be selected within 3–4 h post dose (in order to limit outpatients' stay) and the number of samplings should not exceed three [17, 18]. The selection of the different time points was based on their respective prediction performance.

The predictive performance of MAP Bayesian estimation was evaluated by calculating the prediction error (PE) and absolute prediction error (APE) using the following equations: PE = (Bayesian estimated AUC_0–t– reference AUC_0–t)/reference AUC_0–t and APE = absolute value (Bayesian estimated AUC_0–t– reference AUC_0–t)/reference AUC_0–t. The PE and APE are expressed in the Results as a percentage by multiplying by 100.

Where the AUC_0–t was defined as dose/CL, the individual CL was calculated by MAP Bayesian estimation (‘MAXEVAL = 0’ and ‘Posthoc’ in the $ESTIMATION step of NONMEM software, first-order conditional estimation interaction option) using population pharmacokinetics parameters obtained from the developed model. For each patient, the reference and estimated values were determined by rich multiple time points pharmacokinetics (8 points for q12 and 9 points for q24) and MAP Bayesian estimators (combinations of selection time points 1–3, respectively).

Owing to the limited number of patients in this study, the cross-validation method was used to evaluate MAP Bayesian estimator [17]. The full data set was randomly divided into three subsets (each one contains one-third of the pharmacokinetic profiles). The population parameters obtained in each combination of two subsets (building group) were used as priors to calculate the individual pharmacokinetic parameters of the remaining subset (validation group), respectively. This procedure was repeated three times and the data were analysed by NONMEM software. Estimated AUC_0–t using MAP Bayesian estimator from cross-validation, repeated three times, was then compared with the reference AUC_0–t.

The performance of MAP Bayesian estimator was also evaluated by a simulation–estimation procedure. Firstly, 100 data sets were created using Monte Carlo simulation with the population pharmacokinetics parameters obtained from the developed model, where each simulation cohort consisted of virtual individuals with the same weight distribution as the original data set. Simulated pharmacokinetic profiles were then generated for each of the simulated children with rich multiple time points and Bayesian estimator according to the proposed sampling schedule. Finally, the new simulated data set was modelled in NONMEM utilizing Bayesian estimation as described above. Estimated AUC_0–t using MAP Bayesian estimator was compared with the reference AUC_0–t.

Results

Population pharmacokinetic modelling

Twenty-three children were included in this population pharmacokinetic analysis. Twelve boys and 11 girls, aged 1.8 years (mean, range 0.43–2.89 years) and weighing 11.6 kg (mean, range 7.4–15.9 kg), were enrolled. The characteristics of the patients are presented in Table 1.

Table 1.

Characteristics of the 23 HIV-infected children

	Number	Mean	Range
No. of patients	23
Male/female	12/11
Body weight (kg)*		11.6	7.4–15.9
Age (years)†		1.8	0.43–2.89
Height (cm) †§		81	62–98
Body mass index (kg m–2)†§		17.8	15.0–24.2
Serum creatinine (mg l−1)†‡		34.7	22.1–53.9

^*On the day of pharmacokinetic sampling.

^†Time of inclusion.

^‡Data available for 21 patients.

^§Data available for 22 patients.

Eighteen patients had a full pharmacokinetic profile and five had incomplete pharmacokinetic profile; 347 plasma abacavir concentrations were available for population modelling. The individual abacavir plasma concentrations plot is shown in Figure 1. Of the measured concentrations, 13.5% were below the LLQ, and half the LLQ value was used to handle these concentrations. Data fitted a two-compartment model with first-order absorption and elimination. In the diagnostic plot of CWRES vs. time, no trends were observed. Interindividual variability was best described by an exponential model and was then estimated for Q/F, V₂/F and CL/F. Interoccasion variability on CL/F was coupled to interindividual variability by an additive model. Residual variability was best described by a proportional model.

Figure 1.

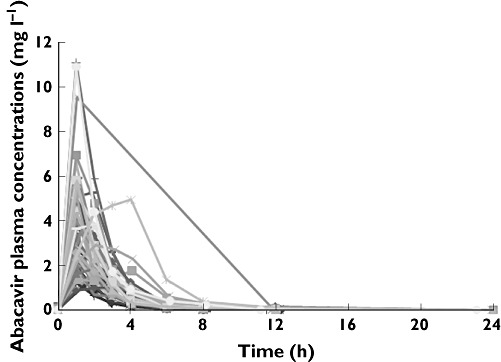
Plot individual abacavir plasma concentrations

The following potential variables were tested: age, gender, weight, height, body mass index, serum creatinine and drug administration frequency. In the covariate selection process, because many age-related covariates were highly correlated in this population, weight was included a priori as a descriptor into the model before confirming other age-related covariates (i.e. age and height). In forward selection processes, inclusion of height, age and weight on CL/F and V₂/F all separately produced a significant decrease in OFV. After preincorporating the weight into the model, age and height were not found to be significant. In the backward selection process, only removing weight from CL/F produced a significant increase of OFV (>6.635, P < 0.01, χ² distribution). Finally, the influence of weight on CL/F was retained in the model with the following equation, which caused 11.9 units decrease in OFV compared with the structure model. The covariates in the selection process are shown in Table 2. The interindividual variability of CL/F decreased from 32.2 to 19.9%.

Table 2.

Covariates selection process

	Pharmacokinetic parameters	Objective function value
Structure model without covariate		−1141.6
Weight	CL/F	−1153.5
Age	CL/F	−1151.0
Height	CL/F	−1151.9
Weight	V2/F	−1146.4
Age	V2/F	−1146.5
Height	V2/F	−1146.3
Weight, age and height	CL/F	−1153.9
Weight and age	CL/F	−1153.8
Weight and height	CL/F	−1153.7
Weight, age and height	V2/F	−1147.3
Weight and age	V2/F	−1147.3
Weight and height	V2/F	−1146.7
Weight	CL/F and V2/F	−1160.0
Weight	CL/F	−1153.5

where CL/F_j is the CL/F of the jth individual, WT_j the weight of the jth individual, WT_ref the reference weight and CL/F_ref the CL/F of an individual with a reference weight. In our study, the reference weight was the median value of our population, 12 kg. The PWR exponent was estimated to be 1.14.

The diagnostic plots indicate acceptable goodness of fit (Figure 2). The mean parameters estimates resulting from the bootstrap procedure very closely agreed with the respective values from the final population model, indicating that the estimates for the population pharmacokinetic parameters in the final model were accurate and that the model was stable. The results of 1000 bootstrap replicates are summarized in Table 3. The shrinkage values for Q/F, V₂/F and CL/F were 35.2, 12.3 and 25.8%, respectively.

Figure 2.

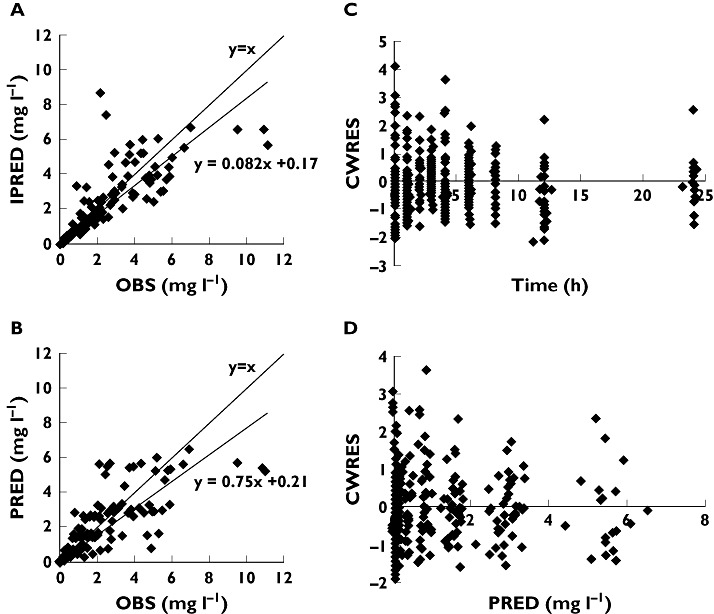
Diagnostic plots. (a) Observed (OBS) vs. individual prediction (IPRED). (b) OBS vs. population prediction (PRED). (c) Conditional weighted residuals (CWRES) vs. time. (d) CWRES vs. PRED

Table 3.

Population pharmacokinetic parameters of abacavir and bootstrap validation

	Final model		Bootstrap n = 1000
Parameters	Final estimate	RSE (%)	Mean	2.5th–97.5th percentile
Absorption rate constant (h−1) Ka	0.758	5.8	0.757	0.724–0.788
Apparent central volume of distribution (l) V1/F	4.94	28.7	4.91	4.09–5.74
Apparent peripheral volume of distribution (l) V2/F	8.12	14.2	8.04	7.22–8.85
Apparent inter-compartment clearance (l h−1) Q/F	1.25	16.9	1.25	1.19–1.30
Apparent systemic clearance (l h−1) CL/F
CL = θ4 × (WT/12)θ5
θ4	13.4	6.3	13.4	12.9–14.0
θ5	1.14	25.1	1.15	1.11–1.19
Residual proportional (%)	14.1	15.2	14.1	12.5–15.4
Interindividual variability (%)
Q/F	30.9	92.6	29.4	26.1–31.0
V2/F	40.2	34.6	42.1	39.7–44.5
CL/F	19.9	54.3	19.9	16.6–22.4
Interoccasion variability (%)
CL/F	21.6	30.8	21.8	19.4–24.3

The visual predictive check is presented in Figure 3. This visual internal validation of the model shows that approximately 90% of abacavir data fit well within the 5th–95th percentiles of simulation (exact binomial test, 6.3% out of limits observed, 95% confidence interval 4.0–9.4) and are symmetrically distributed (Pearson's χ² test, P = 0.2). The NPDEs are presented in Figure 4.

Figure 3.

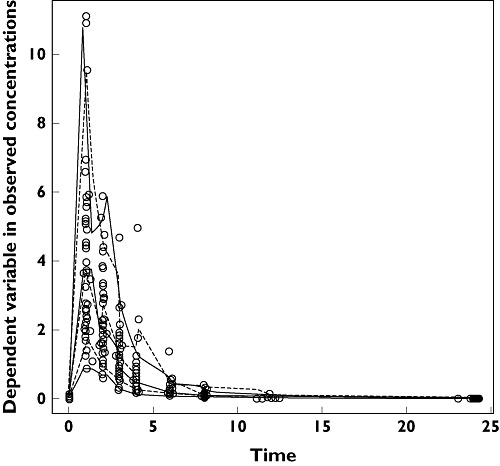
Visual predictive check (VPC). Fifth, 50th and 95th percentiles of observed concentrations; 5th, 50th and 95th percentiles of simulated concentrations

Figure 4.

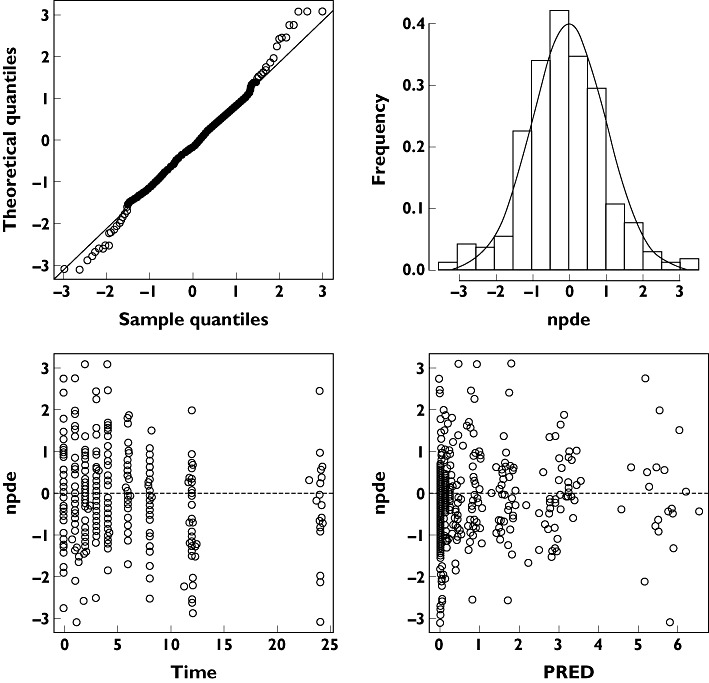
Normalized prediction distribution errors (NPDE)

The mean and variance of NPDE were −0.117 and 1.13, respectively. The NPDE distribution and histogram agrees well with the theoretical N(0, 1) distribution and density, indicating a good fit of the model to the individual data. In the diagnostic plots of NPDE vs. time and predicted concentrations, no trends were observed.

Maximum a posteriori probability Bayesian estimator

The 36 full pharmacokinetic profiles from 18 patients were used to determine the MAP Bayesian estimator. Firstly, the MAP Bayesian estimator was tested with our original data set using estimated pharmacokinetic parameters of the final population model. When one single sample was tested, T3 gave the smallest prediction error, but the APEs of seven pharmacokinetic profiles exceeded 20%. The combination of two samples did not improve the precision, while the combination of three samples T0, T1 or T2, and T3 gave both a satisfactory prediction error and good precision (mean percentage absolute prediction error < 3%, APEs of two pharmacokinetic profiles exceed 20%; percentage APE < 25%).

Further validation was conducted using the cross-validation method described above. Detailed results are presented in Table 4. The prediction errors of MAP Bayesian estimators using the simulation–estimation method are shown in Figure 5. Both methods indicate that the MAP Bayesian estimators of T0, T1 or T2, and T3 are satisfactory for predicting AUC_0–t.

Table 4.

Determination of maximum a posteriori probability Bayesian estimator of abacavir AUC_0–t

	Original data		Cross-validation
Limited sampling strategies	Prediction error (%)	Absolute prediction error (%)	Prediciton error (%)	Absolute prediction error (%)
	Mean ± SD	Mean ± SD	Mean ± SD	Mean ± SD
0 h	8.3 ± 21.3	18.9 ± 12.9
1 h	−5.5 ± 25.9	20.5 ± 16.4
2 h	−3.9 ± 20.7	16.0 ± 13.5
3 h	−0.1 ± 15.8	12.1 ± 10.0
0 h, 3 h	5.6 ± 11.5	10.3 ± 7.4
1 h, 3 h	−3.1 ± 15.8	13.6 ± 8.4
2 h, 3 h	−3.4 ± 15.2	12.4 ± 9.1
0 h, 1 h, 3 h	3.0 ± 11.0	9.7 ± 5.8	0.8 ± 13.5	10.5 ± 8.3
0 h, 2 h, 3 h	2.5 ± 10.6	9.1 ± 5.8	0.1 ± 13.9	11.7 ± 7.3

Figure 5.

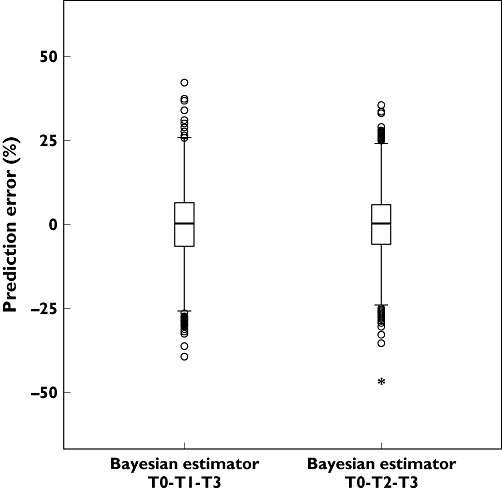
Prediction errors of Bayesian estimators T0-T1-T3 and T0-T2-T3 using simulation–estimation method

Discussion

In the present study, abacavir pharmacokinetics were well described by a two-compartment model with first-order absorption and elimination. Our results are consistent with the findings of a previous population pharmacokinetic study conducted in adults [19]. In contrast, a one-compartment model was reported in two other population pharmacokinetics studies [9, 20]. This discrepancy could be explained by differences in study design, as discussed by Julien et al. [19]. In fact, taking only a limited number of samples within the dosing interval does not allow precise modelling of the distribution and elimination phases.

Weight was incorporated into CL/F with a power model. The exponent coefficient was estimated at 1.14 and was not fixed by allometric scaling. There is still some controversy in the paediatric modelling community on choice of fixed power allometric scaling (0.75 for clearance, 1 for volume of distribution). The allometric scaling has the advantage of accounting for weight difference over a large age range of patients [21]. However, it does not account for maturation of individual processes, such as metabolic clearance via specific enzymatic pathways and it is no longer correlated to size via a standard fixed allometric scaling [22]. This restricts the choice of fixed power allometric scaling in our case, as there are no data available on the ontogeny of abacavir metabolic pathways. It is well known that the maturation rates are different among enzymes and isoforms within the same enzyme family responsible for the metabolism of abacavir [23]. The UGT isoform implicated in abacavir metabolism has not been identified. Hence, the exponential scaling was estimated by the model instead of fixing it. This approach is adapted to paediatric modelling within a narrow age range, especially for young children [24]. It has recently been applied to the pharmacokinetics of morphine in children aged <3 years, including preterm and term neonates, in which an estimated exponent of 1.44 adequately described clearance [25]. After incorporating weight, the age and height were not significant. Given the small number of patients and their narrow age range, this may simply indicate a lack of information about these covariates. Large data sets would be required to confirm the covariate–parameter relationship and to develop the abacavir maturation model across the entire paediatric age range.

The covariate analysis did not show a significant difference between once and twice daily dosing of abacavir. The VPC simulation also indicated that the model predicts well both the once and twice daily pharmacokinetic profiles. This supports the findings of the PENTA13 and PENTA15 trials [11, 26], which demonstrated the bioequivalence of daily doses of abacavir given once and twice daily in HIV-infected children.

Unlike the other nucleoside reverse transcriptase inhibitors, in which the relationship between plasma concentrations and efficacy and/or toxicity is unclear, the AUC of abacavir has been correlated significantly with efficacy [9]. The recommended dose is 8 mg kg⁻¹ twice daily (up to a maximum of 300 mg twice daily) in children aged from 3 months to 16 years, but as shown in the PENTA 15 trial, large interindividual variability in plasma drug concentrations is observed, with AUC_0–24 ranging from 4.93 to 22.03 µg h ml⁻¹[11]. These findings suggest that variability in small children may be higher than what is observed in older children and adults, and will result in high variability in drug concentrations if a standard dosage regimen is used in infants and toddlers. Further evaluation of the extent of variability in clearance due to factors other than weight should be considered, i.e. physiological variables and ontogeny of abacavir metabolic pathways. Indeed, ontogeny has been well documented for UGT. In vitro, Strassburg et al. demonstrated that children had lower hepatic glucuronidation activities than adults [23]. In vivo, low glucuronidation activities in children were characterized for morphine (UGT2B7), paracetamol (UGT1A6) and propofol (UGT1A9) [27]. The identification of the responsible UGT isoforms and genotype–phenotype studies should be evaluated in further research.

The correlation between blood/plasma drug concentrations and clinical outcomes is an important factor to support TDM in order to optimize therapeutic efficacy and minimize adverse events. Given the mechanism of action of abacavir, the pharmacokinetic–pharmacodynamic relationship can be assumed to be similar across all age groups, including infants and toddlers, and the AUC_0–12 target value of 6.02 µg h ml⁻¹ determined in adults can be set as TDM targeted exposure in children. However, measuring a full AUC profile is not a viable option for routine use, in particular for young children. The MAP Bayesian estimation of AUC is more feasible and is increasingly employed in AUC guided TDM for immunosuppressants, antibiotics and anticancer drugs in children [28]. Indeed, this methodology takes into account the pharmacokinetic characteristics of a typical population, individual data collected from studies of patients, such as drug concentrations and covariates, and also considers the variability of the pharmacokinetic parameters in the study population. The published abacavir population pharmacokinetic model in this population still has some limitations for clinical use, as it was developed using sparse sampling [20], which might introduce bias in individual prediction of AUC. In addition, the once daily abacavir pharmacokinetic profile, which gave higher maximum concentrations, was not incorporated in the developed model for the estimation of population pharmacokinetic parameters. This might also introduce bias in predicting the AUC of the once daily regimen. The present study was conducted to overcome these limitations by providing a clinically reliable MAP Bayesian estimator based on several pharmacokinetic samples and a validated population pharmacokinetic model. This a posteriori dosing adjustment tool will facilitate the abacavir dosage individualization in infants and toddlers, who have shown large interindividual variability in plasma concentrations with a standard dosing regimen.

After cross-validation and simulation–estimation, the combination of three samples (T0, T1 or T2, and T3) gave the best predictive performance for individual AUC_0–t of abacavir. The predictive precision decreased with a reduction in the number of combined samples.

In summary, as abacavir pharmacokinetics was highly variable in infants and toddlers, the present population pharmacokinetic model was developed in HIV type-1-infected children aged 3–36 months and adequately described both once and twice daily pharmacokinetic profiles. Weight was identified as a significant covariate influencing abacavir CL/F. We then developed a MAP Bayesian estimator of AUC_0–t from the final model, based on patients' weight and a limited number of abacavir concentrations (T0, T1 or T2, and T3). Although the clinical improvement of dosage adaptation following monitoring remains to be evaluated for all antiretroviral drugs [5, 29], AUC guided abacavir dosing adjustment should be recommended in infants and toddlers, as HIV treatment is expected to be lifelong and children undoubtedly need convenient and acceptable methods to optimize exposure [30, 31].

Competing Interests

There are no competing interests to declare.