Skip to main content
. 2012 Jun 18;7(6):e39059. doi: 10.1371/journal.pone.0039059

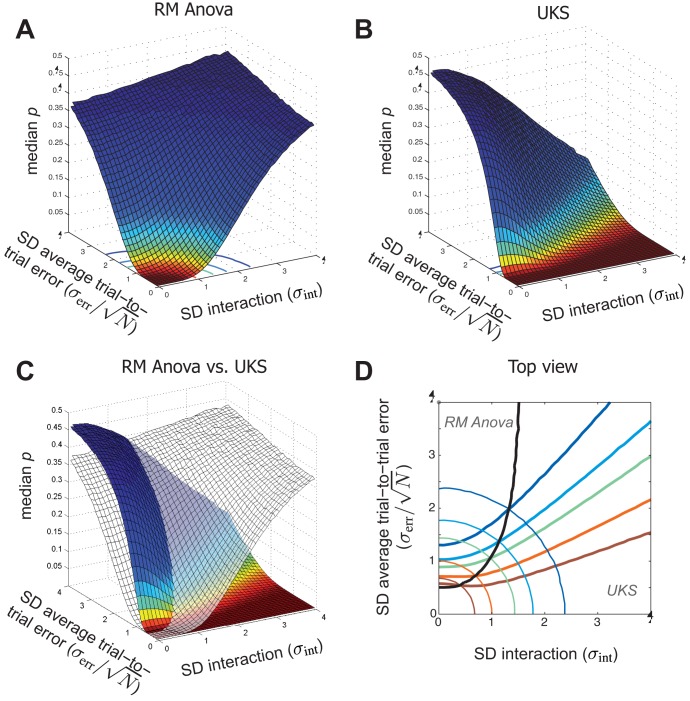
Figure 1. Comparison of type II error rates in UKS test and RM Anovas.

Figure 1

. Results of a simulation study based on over one billion datasets. Each dataset represents the data of 10 individuals performing 10 trials in each of the 2 levels of a factor. Each data point was obtained by adding to the fixed central value of the level (−1/√2 or +1/√2) two random Gaussian values representing individual idiosyncrasies and trial-to-trial errors (see Methods). Panel A: Median probability (Z-axis) yielded by RM Anovas as a function of the standard deviations of subject-factor interaction (X-axis, rightwards) and average of 10 trial-to-trial errors (Y-axis, leftwards). Panel B: Median probability yielded by the UKS test for the same random data. Panel C: superimposition of the surfaces displayed in panel A and B. Note that in conditions when UKS test is less powerful than ANOVA (larger median p), the difference in power is never dramatic; the converse is not true. Panel D: 2D-isolines of the surfaces in panel C for median probabilities. 001 (red), .01 (orange), .05 (green), .10 (light blue) and .20 (dark blue). Black line: projection of the intersection of the two surfaces; RM Anova is more powerful (smaller median probability) than the UKS test for points leftwards of the black line. Note that scaling the X-axis to the SD of within-level averages of trial-to-trial errors gives a symmetrical aspect to RM Anova surface and projection.