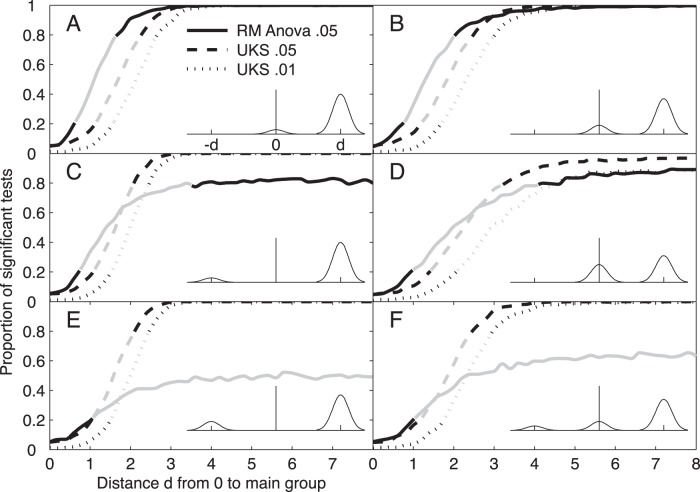
Figure 2. Type II errors and reproducibility with heterogeneous experimental effects.

. Each panel displays the proportion of significant hypothetical experiments as a function of the difference d between the constant values of experimental effect in 2 (panels A–E) or 3 sub-populations (panel F). The lines show the proportion of significant tests in 10000 hypothetical experiments for 41 values of d from 0 to 8 by .2 steps for RM Anovas (continuous line) and the UKS test at both the .05 (dashed line) and.01 threshold (dotted line). The gray part of lines indicates the 0.211–0.789 range of proportion of significant tests for which the probability that two subsequent experiments yield conflicting outcomes exceeds 1/3. Each experiment consists in 10 individuals performing 8 trials in a baseline condition and in an experimental condition. Trial errors are drawn from a Gaussian distribution with parameters 0 and √8, so that the average of the experimental condition has a Gaussian distribution centered on –d, 0 or +d (Insets) with unitary variance. The proportion and center of the subpopulations varied across studies. In the first study (panel A), the experimental effect was set to 0 for 10% of the population, and to d for the remaining 90%. In the other studies (Panels B–F), the effects and proportions were as follows: [0, 20%; d, 80%]; –d, 10%; d, 90%]; [0, 40%; d, 60%]; –d, 20%; d, 80%]; [–d, 10%; 0; 20%; d, 70%]. For each hypothetical experiment, the 10 individual effects were drawn with replacement from a set of –d, 0 and +d values in the above proportions (for d = 0, the proportion of significant tests is equal to the nominal type I error rate). We conclude that when factor effects vary across individuals as modeled by a mixture of Gaussians, UKS tests yield more reproducible outcomes than RM Anovas and have lower type II errors.