Dynamics of spatial frequency tuning in mouse visual cortex

Abstract

Neuronal spatial frequency tuning in primary visual cortex (V1) substantially changes over time. In both primates and cats, a shift of the neuron's preferred spatial frequency has been observed from low frequencies early in the response to higher frequencies later in the response. In most cases, this shift is accompanied by a decreased tuning bandwidth. Recently, the mouse has gained attention as a suitable animal model to study the basic mechanisms of visual information processing, demonstrating similarities in basic neuronal response properties between rodents and highly visual mammals. Here we report the results of extracellular single-unit recordings in the anesthetized mouse where we analyzed the dynamics of spatial frequency tuning in V1 and the lateromedial area LM within the lateral extrastriate area V2L. We used a reverse-correlation technique to demonstrate that, as in monkeys and cats, the preferred spatial frequency of mouse V1 neurons shifted from low to higher frequencies later in the response. However, this was not correlated with a clear selectivity increase or enhanced suppression of responses to low spatial frequencies. These results suggest that the neuronal connections responsible for the temporal shift in spatial frequency tuning may considerably differ between mice and monkeys.

the structural and functional layout of the rodent visual system is similar in many aspects to that of carnivores or primates. However, there are some significant differences. Besides the general absence of a gyrated cerebral surface and laterally placed eyes, the rodent primary visual cortex lacks ocular dominance columns and is subdivided into small binocular and larger monocular regions (Hubener 2003; Tagawa et al. 2005; van Brussel et al. 2009). Moreover, orientation-tuned cells in mouse and rat V1 are not clustered in columns of similar orientation preference, as in cats and monkeys, but are randomly dispersed throughout V1 in a “salt-and-pepper pattern” (Mrsic-Flogel et al. 2007; Ohki et al. 2005). The lack of a columnar organization in V1 is not confined to nocturnal rodents such as rats and mice that do not rely on vision as much as primates for gaining information about their environment. Squirrels intensely rely on vision for their arboreal lifestyle yet equally lack orientation columns (Van Hooser et al. 2006; Van Hooser et al. 2005).

Despite these differences, neurons in rodent V1, and mouse V1 in particular, are highly tuned to a narrow range of stimulus parameters. For example, mouse V1 neurons show relatively sharp tuning for orientation, spatial frequency, temporal frequency, contrast, as well as stimulus length or size (Gao et al. 2010; Niell and Stryker 2008; Van den Bergh et al. 2010). While some aspects of neuronal responses, e.g., much larger receptive fields (RFs) and lower visual acuity, and a substantially lower level of surround suppression in mouse V1, can be different from those in primates, other tuning parameters are remarkably similar. The bandwidth for spatial frequency of neurons in mouse V1 when measured in octaves is similar to the spatial frequency bandwidth recorded in macaque or cat V1 (Gao et al. 2010; Van den Bergh et al. 2010), suggesting that similar circuitry in the visual system of rodents could be responsible for generating neuronal selectivity for spatial frequency.

Previous studies in cats and monkeys have shown that the spatial frequency tuning of V1 neurons changes over short time spans. V1 neurons are at first selective to lower spatial frequencies but gradually develop selectivity for higher spatial frequencies (Bredfeldt and Ringach 2002; Mazer et al. 2002; Nishimoto et al. 2005). This temporal shift in preferred spatial frequency can be attributed to an increase in the spatial frequency selectivity over time, generated by the suppression of lower spatial frequencies (Bredfeldt and Ringach 2002). While these spatial frequency tuning dynamics are clearly observable in the primary visual cortex, they might partly originate in the lateral geniculate nucleus (LGN) (Allen and Freeman 2006). In the wulst of the burrowing owl, a V1 analog in birds, similar temporal changes in spatial frequency tuning were observed without a parallel shift in preferred spatial frequency (Pinto and Baron 2010).

In an attempt to determine whether the spatial frequency tuning of individual neurons in mouse visual cortex depends on similar neuronal connectivity to that in macaque monkeys or cats, we analyzed the dynamics of spatial frequency tuning in mouse V1 using a similar reverse-correlation method to that used in monkey V1 (Bredfeldt and Ringach 2002). We also compared the dynamics of spatial frequency tuning between V1 and the extrastriate lateromedial (LM) field, which is a part of the lateral V2 complex (V2L) (Andermann et al. 2011; Marshel et al. 2011; Wang and Burkhalter 2007; Wang et al. 2011). Our data show that, as in cats and monkeys, neurons in mouse visual cortex showed a clear shift in the preferred spatial frequency from low to high although this is not accompanied by an increase in tuning selectivity. There were no significant differences in the temporal spatial frequency tuning characteristics between V1 and LM in mice except for the strength of suppression.

MATERIALS AND METHODS

Subjects

Microelectrode recording experiments were conducted in anesthetized mice of the C57Bl/6 strain ranging in age from 3 to 5 mo (n = 9), housed under a conventional 13:11-h light-dark rhythm. All experiments were approved by the Ethical Committee of the university and were in strict accordance with the European Communities Council Directive of November 24th, 1986 (86/609/EEC).

Preparation

Mice were first given an intraperitoneal injection of the antipsychotic Chlorproxithene (5 μg/g body wt) to reduce the dose of urethane required to fully anesthetize the animals. Five minutes later, mice were anesthetized with urethane (1.2 mg/g body wt ip), the most common anesthesia used to study cortical physiology in mice, and, if necessary, additional doses of 0.2–0.3 mg/g body wt urethane were given to induce surgical anesthesia. A tracheotomy was performed, and a short plastic tube was inserted in the open end of the trachea, just below the larynx. A larger plastic tube blowing 95% oxygen-5% carbon dioxide was placed in front of the opening of the trachea tube enriching the inhaled room air with oxygen. The animal's core temperature was kept at 37.5°C. The animal was mounted in a custom-built stereotaxic frame with the head held in place by two ear bars with fine tips (1.5 mm) and a mouth bar that fixed the upper incisors. Two electrocardiograph leads were inserted subcutaneously at the left and right side of the thorax to continuously monitor the heart rate, enabling us to assess the depth of anesthesia and the physiological condition of the animal, which is crucial for obtaining good visual responsiveness. The animal's corneas were protected from drying out by regular application of silicon oil. With this procedure, we could maintain the reasonably good optical quality of the eyes. Because the nictitating membrane in mice does not block the cornea under anesthesia and the residual eye drift following urethane anesthesia (without paralysis) is negligible with respect to the large RF sizes in mice (Drager 1975; Gordon and Stryker 1996; Wagor et al. 1980; Wang and Burkhalter 2007), there was no need to employ special procedures to control these potential issues of their physiological optics. The ipsilateral eye was masked by a black cap over the eyeball, and responses were only recorded from the contralateral, right eye. A small (0.5 mm) craniotomy was performed over the central, binocular region of V1 of the left hemisphere. After the opening was made, the dura mater was locally removed using a sharp scalpel. The exposed brain was covered with a drop of mineral oil to prevent drying. Cardiac or respiratory pulsations of the brain surface could not be observed when making these small craniotomies.

Recording and Visual Stimulation

Tungsten-in-glass electrodes were used for isolating the activity of individual cortical neurons. The impedance of our electrode (tip impedance of ∼1 or 9 MΩ) was higher than that of the silicon electrodes employed by Niell and Stryker (2008). We found that, with our electrodes, we could obtain both good isolation and excellent stability in mouse primary and extrastriate visual areas (as reported by many investigators in the visual cortex of higher species). The angle of the penetration was about 45° to the surface because the vertically oriented electrode entered the surface that had a slope of about 45° around the border between V1 and the lateral visual areas (Van den Bergh et al. 2010). This location of electrode penetration with respect to visual areas was determined according to the published map of V1 and its adjacent visual areas, response properties of neurons, and histological examination of electrode tracks (Kalatsky and Stryker 2003; Wagor et al. 1980; Wang and Burkhalter 2007).

Action potentials were extracellularly recorded and amplified using conventional methods. We searched for well-isolated units, and, if we encountered multiple units, we discriminated responses from these units using appropriately placed time-voltage windows. Our recordings started from the brain surface and ended either when the electrode entered the white matter or the animal's deteriorated physiological situation precluded further recordings. Thus we typically sampled through all layers of cortex with intervals of at least 50 μm between subsequent cells. We determined RF positions as described earlier (Van den Bergh et al. 2010) by manually moving small circular optimized drifting gratings (10°) across the screen and locating the position where these gratings produced the strongest response. For mice, the center of the RF in the great majority of our units was located within 20° of the center of the visual field, with only a few units as far out as 60°. We did not dilate the pupil and did not determine the position of the optic disc to prevent a reduction in visual acuity. Because we could not use the optic disc as a reference point, we used the vertical plane through the midline of the animal as the vertical meridian, whereas the horizontal plane through the center of the eye was defined as the horizontal meridian. Recorded action potentials were digitized at 25 kHz, sampled at a rate of 60 Hz (16.7-ms bin widths for drifting grating experiments), and compiled into peristimulus time histograms that were equal in duration to and synchronized with the temporal cycle of the grating, by using data acquisition systems (System III; Tucker-Davis Technologies, Alachua, FL).

Visual stimuli were generated using custom-developed stimulation software using Matlab (The MathWorks, Natick, MA) and the Psychophysics Toolbox (Brainard 1997; Pelli 1997). Stimuli were presented on an LCD monitor (frame rate = 60 Hz, mean luminance = 27 cd/m², 1,280 × 800 pixels, 87° × 66°) at a distance of 25 cm from the eyes either perpendicular to the rostrocaudal axis of the animal for RFs at <30° from this axis, or at an angle of 45° for RFs at >30°. This limited distortion of the visual stimuli for RFs at higher azimuths.

RFs were first mapped on the tangent screen using moving dark edges. Optimal orientation and spatial frequency were quantitatively analyzed by showing drifting sinusoidal gratings that covered the entire monitor screen with a temporal frequency of 3 Hz and a contrast of 99%. Stimulus presentations were interleaved with blank gray screens of mean luminance to determine the spontaneous activity of the units. Spontaneous activity was subtracted from visually evoked responses before tuning curves were analyzed. In all tests, stimulus conditions were shown two times for 10 cycles (3 s at 3 Hz) in random order and interleaved with ≥3 s of gray background. For orientation tuning, 12 equally spaced orientations, 30° apart, were shown at near-optimal spatial frequency [generally around 0.02–0.06 cycles/degree (cpd)]. Spatial frequency was then analyzed at the optimal orientation by presenting drifting sinusoidal gratings with 11 different spatial frequencies ranging from 0.002 to 1.6 cpd. Stimuli were always presented monocularly to the eye contralateral of the hemisphere being sampled. Orientation and spatial frequency tuning were analyzed as described earlier (Van den Bergh et al. 2010).

Dynamics of Spatial Frequency Tuning

Dynamics of spatial frequency tuning were measured and analyzed using the reverse-correlation technique described by Bredfeldt and Ringach (2002). It is important to keep in mind that we employed the identical reverse-correlation method developed by Ringach et al. (1997) and extensively used in Bredfeld and Ringach (2002) to optimize the comparisons between macaque monkeys and mice with respect to dynamics of spatial frequency tuning in V1. Responses were recorded from individual cells of mice that were shown a rapid sequence (60 Hz) of luminance-modulated sinusoidal gratings with an orientation fixed at the optimal orientation of the cell, as measured using drifting sinusoidal gratings, and varying spatial frequencies and spatial phases. The luminance contrast (Michaelson contrast) was 99%. Spatial frequencies ranged from 0.0025 to 0.32 cpd in half-octave steps, encompassing most of the response ranges for spatial frequencies for all the cells we analyzed. Each of the spatial frequencies was shown for eight spatial phases, equally spaced and spanning 360°. Interleaved were blank gray images of uniform mean luminance that were shown to assess the cell's baseline response. The probability of showing a blank image was equal to that of showing any one spatial frequency, irrespective of spatial phase. Stimuli were shown across a full screen to enable the stimulation of both the RF center and surround. Each sequence consisted of 512 images drawn randomly from the image set of all spatial frequencies, spatial phases, and blanks and lasted ∼9 s. Ninety sequences were shown with an interval of about 1.5 s, for a total experiment time of 15 min.

For each action potential the cell fired during visual stimulation, we recorded its arrival time. For each time lag τ, with 1 ms resolution, we determined the probability that a spike was preceded by a particular grating with a spatial frequency f at a particular time delay τ, independent of spatial phase: Pr(f,τ). The probability that a blank image with uniform luminance preceded a spike at a specific delay time τ was called the baseline B(τ). Because the blank stimuli we used might drive the cells to a steady-state response that is above their spontaneous firing rates, this baseline response probability should more accurately reflect a maintained response level. The relative strength of the response to a given stimulus grating compared with the baseline (or maintained) response probability was then calculated:

$$R\left(f,\tau \right)={\log }_{10}\left\{\frac{Pr\left(f,\tau \right)}{B\left(\tau \right)}\right\}$$

We analyzed the spatial frequency tuning dynamics by calculating R(f,τ) at τ values ranging from 0 to 200 ms. R(f,τ) values of zero indicate that the cell's response to a test stimulus was equal to that of the blank stimulus. Positive values indicate response enhancement while negative values correspond with suppression of the response (Fig. 1). Before τ = 30 ms and after τ = 150 ms, R(f,τ) should be at zero, indicating that there is no increased response probability at these lag times, while between 30 and 150 ms increased or decreased response probabilities can occur.

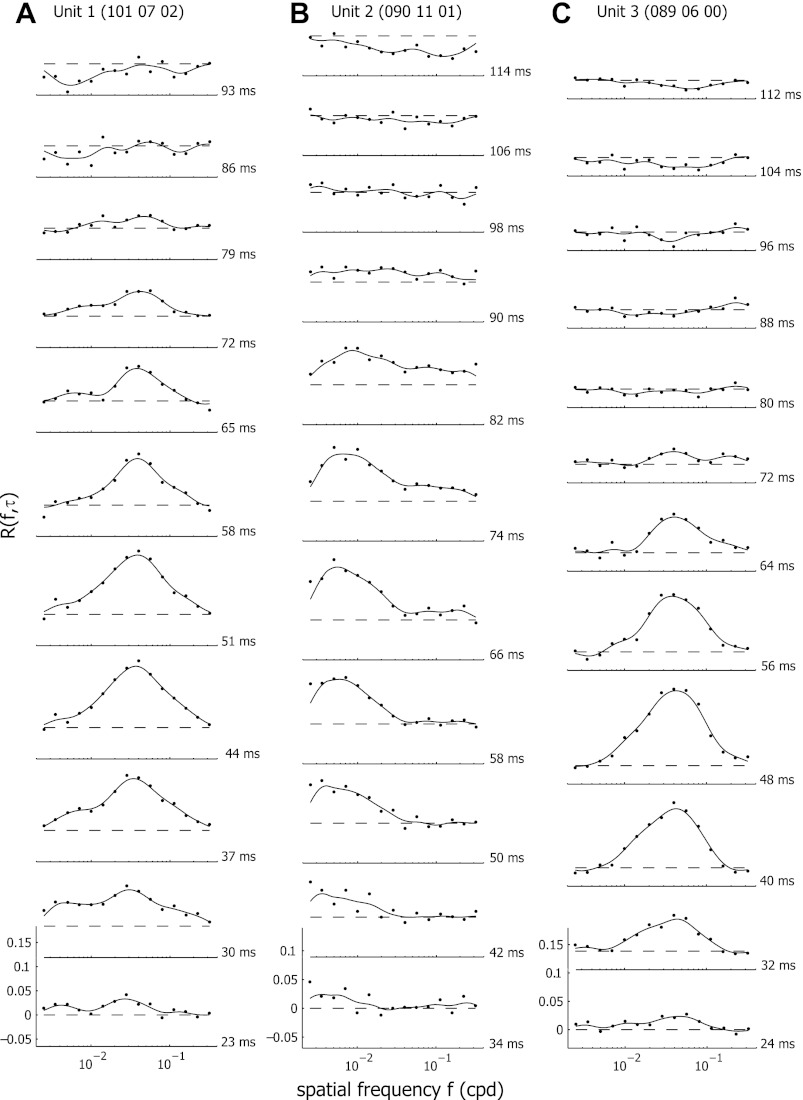
Fig. 1.

Examples of temporal dynamics of spatial frequency tuning for three representative neurons (A-C). The response tuning curves at different time delays are shown. The dashed lines indicate the baseline response level. Responses above this line are excitatory; responses below this level are suppressive.

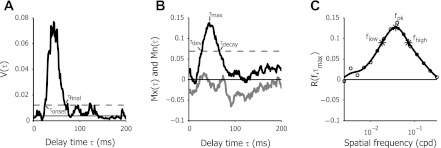
To determine the time of response onset (τ_onset) and decay (τ_final), we looked at the variance of the response over time (Fig. 2A). For short time delays, before the signal has reached the visual cortex, the deviation of the response from the zero baseline is due to measurement noise. When the cell responds to the stimulus, it responds by deviating strongly from the baseline. The magnitude of these deviations is reflected by the variance of the signal (across all spatial frequencies) at each time delay:

$$V\left(\tau \right)={\displaystyle \sum _{f}R{\left(f,\tau \right)}^2}$$

The mean of the variance of the response at the first 20 ms [V̄(τ ≤ 20)] was used to estimate the variance of the noise. For time delays with a stimulus-driven response, the variance increased significantly. We defined τ_onset and τ_final as the first and last time lags τ at which the variance of the response V(τ) crossed a threshold of 4 SD of the variance of the response at the first 20 ms above the mean variance of the noise (Bredfeldt and Ringach 2002).

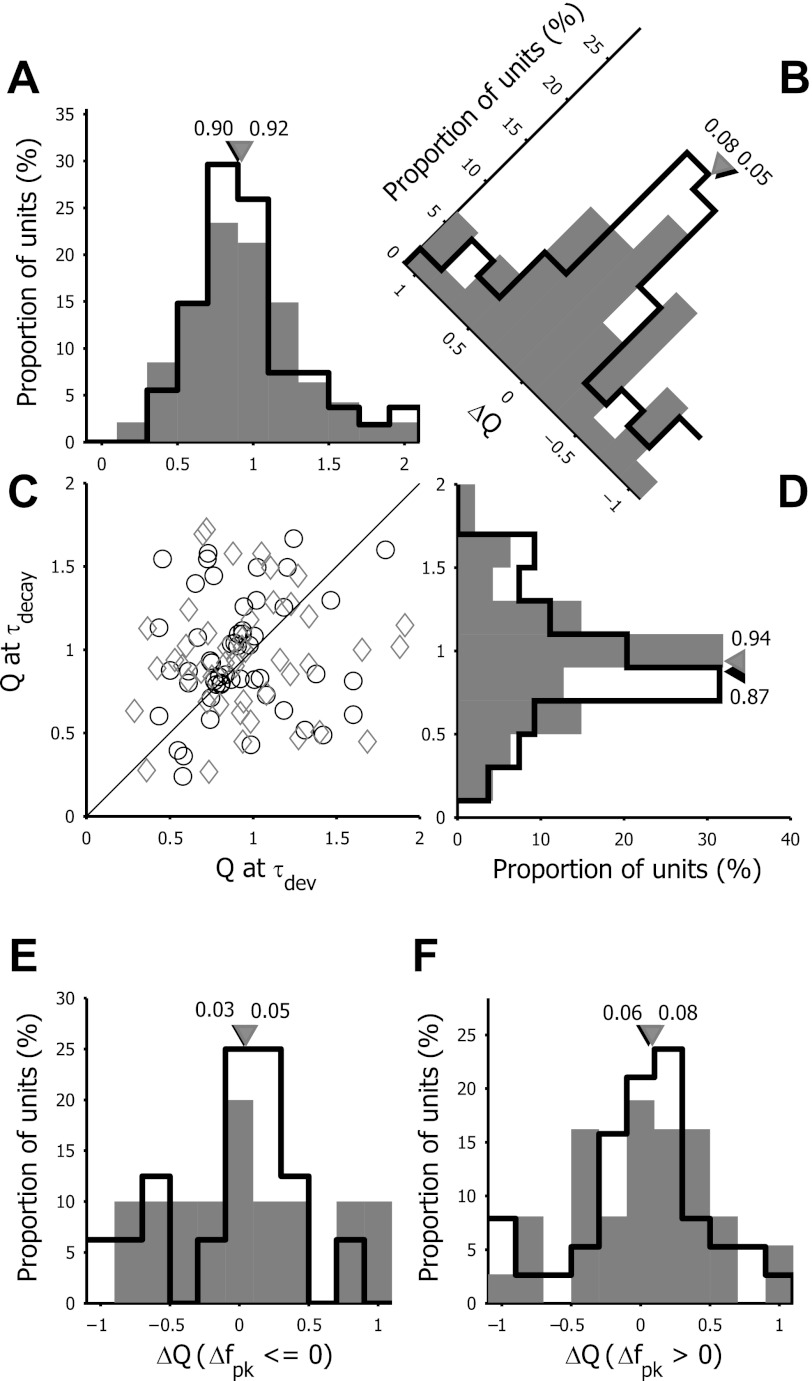
Fig. 2.

Analysis of spatial frequency tuning dynamics. A: variance (V) of the response to different spatial frequencies over different delay times (τ) for a representative neuron. The solid line indicates the mean variance over the first 20 ms. The dashed line indicates the criterion level of response significance. Where the variance crosses the criterion line defines τ_onset and τ_final. B: maximum [Mx(τ), black line] and minimum [Mn(τ), gray line] response level times as a function of τ. τ_max is the time delay where the response reached maximal levels. The dashed line corresponds to half the maximal response levels. τ_dev and τ_decay, respectively, are defined to the delay times where the maximal response levels crossed this level during development and decay of the response. C: response for different spatial frequencies at τ_max. Circles show the measured response levels for 15 different spatial frequencies relative to baseline response [R(f,τ_max) = 0]. Responses below 0 correspond with response suppression. The thick line is the smoothed response level, used to estimate f_pk, the spatial frequency that produced the highest response level. f_low and f_high mark the low and high spatial frequency cutoffs, respectively, and are used to calculate the quality (Q)-factor.

The maximum and minimum amplitudes of the response were defined as

$$\text{Mx}\left(\tau \right)={\max }_f\left[R\left(f,\tau \right)\right]\text{and}\text{Mn}\left(\tau \right)={\min }_f\left[R\left(f,\tau \right)\right]$$

respectively (Fig. 2B). Because these maximum and minimum amplitudes vary over time, τ_max and τ_min indicate the time lag that showed strongest response enhancement or response suppression, respectively. We also defined τ_dev and τ_decay as the time lag where Mx(τ) reached or decayed back to half its maximum amplitude R(f_pk,τ_max)/2.

For each time lag τ we analyzed the spatial frequency tuning curves. To reduce the effects of noise, we smoothed the raw data by interpolating to 300 log-spaced data points and convolving with a Gaussian curve with a σ of 0.4 log units. The peak of the spatial frequency tuning curve, the preferred spatial frequency f_pk at delay τ, was defined as the peak of the smoothed tuning curve.

To analyze the change of f_pk over time, we compared the peak spatial frequency f_pk over time by calculating the overall change in location of the preferred spatial frequency at τ_dev and τ_decay, in spatial frequency octaves:

$$\Delta f_{\text{pk}}={\log }_2\left[\frac{f_{\text{pk}}\left({\tau }_{\text{decay}}\right)}{f_{\text{pk}}\left({\tau }_{\text{dev}}\right)}\right]$$

We also estimated the preferred spatial frequency of the cell for the time-averaged tuning curve:

$$\overline{R}\left(f\right)=\frac{1}{\left({\tau }_{\text{final}}-{\tau }_{\text{onset}}\right)}{\displaystyle {\int }_{{\tau }_{\text{onset}}}^{{\tau }_{\text{final}}}R\left(f,\tau \right)d\tau }$$

This time-averaged peak spatial frequency will be referred to as f̄_pk.

To analyze spatial frequency tuning selectivity, we used the “quality factor” of the tuning curve (Bredfeldt and Ringach 2002), given by

$$\text{Q}\left(\tau \right)=\frac{f_{\text{pk}}\left(\tau \right)}{f_{\text{high}}\left(\tau \right)-f_{\text{low}}\left(\tau \right)}$$

with f_high(τ) and f_low(τ) the high and low spatial frequency cut-offs, the spatial frequencies where the tuning curve drops below R(f_pk,τ)/sqrt(2). f_pk(τ) is the preferred spatial frequency at time τ (Fig. 2C). Cells with sharp spatial frequency tuning have a larger Q-factor, whereas cells with broad tuning have a Q-factor close to zero. Using the Q-factor to determine selectivity is advantageous over traditional methods such as spatial frequency bandwidth, since it allows for the analysis of low-pass-tuned responses, whereas spatial frequency bandwidth is undefined in this case (Bredfeldt and Ringach 2002).

To analyze changes in tuning selectivity over time, we define the change in selectivity as

$$\Delta \text{Q}={\text{Q}}_{\tau \text{decay}}-{\text{Q}}_{\tau \text{dev}}$$

Positive values of ΔQ indicate increased selectivity over time, whereas negative values indicate the cell became less selective over time.

To examine the steepness of the high and low spatial frequency limbs in our data, we use two indexes that allow us to separately analyze the low- and high-frequency flanks of the tuning curves:

$$M_{\text{L}}=\frac{f_{\text{low}}}{f_{\text{pk}}}\text{and}{M}_{\text{H}}=\frac{f_{\text{pk}}}{f_{\text{high}}}.$$

An index close to zero indicates the spatial frequency limb has a shallow curve, whereas a steep curve is indicated by an index close to one.

In addition to the above selectivity measures that were used by Bredfeldt and Ringach (2002), we also computed an alternative and more global measure for tuning curve selectivity: low spatial frequency suppression (LSFS) (Xing et al. 2004) and analogously high spatial frequency suppression (HSFS). This corresponds, respectively, to the ratio between the response at the lowest spatial frequency tested and the response at the optimal spatial frequency (LSFS), and the ratio of the response at the highest spatial frequency tested and the response at the preferred spatial frequency (HSFS). The time-dependent changes in LSFS and HSFS were defined as follows:

$$\Delta \text{LSFS}=\text{LSFS}\left({\tau }_{\text{decay}}\right)-\text{LSFS}\left({\tau }_{\text{dev}}\right)\text{and}\Delta \text{HSFS}=\text{HSFS}\left({\tau }_{\text{decay}}\right)-\text{HSFS}\left({\tau }_{\text{dev}}\right)$$

Strength of response suppression was measured as the ratio of the area of suppression vs. the total area beneath the curve, including enhancement and suppression over τ delay values ranging from τ_dev and τ_decay, as well as from τ_decay to 150 ms:

$$\text{SupIndex}=\frac{{\displaystyle {\sum }_{\tau }{\text{A}}_{\text{S}}\left(\tau \right)}}{{\displaystyle {\sum }_{\tau }{\text{A}}_{\text{S}}\left(\tau \right)+{\text{A}}_{\text{E}}\left(\tau \right)}}$$

A_E(τ) and A_S(τ) are approximations of the excitatory and suppressive area under the curve.

The analysis of the phase dependence of the response enabled us to make a distinction between simple and complex cells, by calculating the F1-to-F0 ratio from the phase modulation at τ_max. We found only six cells with simple cell-like characteristics (F1/F0 > 1), which was not sufficient to make any reliable conclusions about possible differences in the spatial frequency tuning dynamics between simple and complex cells. Moreover, although we did not determine the optimal phase for simple cells but analyzed our data independent of spatial phase, this should not have affected our results because only six units were simple cells and our population thus primarily consisted of complex cells.

For neuronal response characteristics that showed normal distribution, we used standard parametric tests; otherwise, we used median values to evaluate these cellular properties and a Kruskal-Wallis rank test to test the significance of differences.

Histology

At the end of each penetration, two small electrolytic lesions (5 s, 10 μA, electrode negative) were made along the electrode track at intervals of ∼500 μm. The animals were given an overdose of pentobarbital sodium (Nembutal), intraperitoneally, and transcardially perfused with 1% paraformaldehyde in 0.15 M PBS (pH 7.4) followed by 4% paraformaldehyde in 0.15 M PBS (pH 7.4). Vibratome sections were cut and Nissl stained with thionine stain following standard procedures. Photographs of the histological patterns were obtained with a Zeiss Axio-Imager equipped with a Zeiss Axiocam. Brightness and contrast were adjusted using Adobe Photoshop CS2. Areal location and depth of the recording sites were reconstructed based on the positions of the electrolytic lesions and the recording depths along the electrode track as previously described (Van den Bergh et al. 2010). Because there appeared to be little layer-dependent differences in spatial frequency tuning dynamics and the variability of spatial frequency tuning properties within layers was generally as large as in the total cell population, we only placed our cells in subgroups based on areal location, but not based on depth or layers. Because the sample size for each layer was small, a larger sample would be required to make conclusive statements about layer differences.

All recording sites lateral of V1 were located in the lateral complex of visual areas, which is called lateral V2 (V2L) by Franklin and Paxinos (2008), recently described to comprise two different areas (Van der Gucht et al. 2007; Wang and Burkhalter 2007; Wang et al. 2011). The use of coronal Nissl-stained sections did not allow to exactly define the border between the two areas along the anterior-posterior axis in our histological analysis. Nevertheless, based on the position of the anterolateral (AL) and LM areas relative to V1 in cortical flat maps (Wang and Burkhalter 2007; Wang et al. 2011), the position of our electrode tracks along the anterior-posterior axis (between 2.0 and 3.6 mm posterior from bregma) and the fact that we were generally recording from the upper visual field in V1 before we crossed the V1/V2L complex border, we are confident that the recording sites outside V1 were all in LM and not in AL.

Data Selection

We recorded responses from 181 units from 9 mice. All cells in our analysis were stimulated with gratings oriented to within 30° of their preferred values. We excluded 66 units that did not show a significant response, i.e., where V(τ > 20) was less than 4 SD above the average variance of the noise [V̄(τ ≤ 20)]. Twelve cells were excluded because their responses for the highest spatial frequencies were not at baseline. For two more cells, we could not get histological verification of cortical layer and visual area. A total of 101 cells passed these criteria and were thus included in the dataset comprising this study. The percentage of cells that passed these criteria (56%) was only slightly lower than the percentage of cells passing similar criteria in monkeys (61%) (Bredfeldt and Ringach 2002).

RESULTS

The goal of this study was to determine whether the development of spatial frequency tuning of mouse visual cortex neurons at a fine time scale was comparable to that of monkeys and cats. To this end, we quantitatively analyzed the temporal dynamics of spatial frequency tuning of 181 neurons in nine mice using a reverse-correlation method in the spatial frequency domain. For 101 cells, we obtained a significant response to the stimulus, 54 cells from V1 and 47 from LM. All units came from the binocular region of these areas, with most neurons located within 30° of the vertical meridian. The stimuli used for reverse correlation consisted of short movies of sine wave gratings of optimal orientation with spatial frequency and phase randomly changing at 60 Hz. We showed 15 different spatial frequencies, each at 8 different spatial phases. We averaged the reverse-correlated responses across all spatial phases.

Figure 1 shows the dynamic response of three representative cells. The response rate relative to the maintained discharge level, R(f,τ), is plotted for delays ranging from 23 to 114 ms. A dashed line at R(f,τ) equal to 0 indicates the response level to a blank stimulus of mean luminance. Positive values signify response enhancement to a specific spatial frequency, whereas negative values point to suppression below the response level of the blank stimulus. All three units showed a first observable response R(f,τ) at a delay time τ of around 30–35 ms. This response gradually increased in strength, reaching a maximum after 48–66 ms, followed by a gradual decrease in response, returning to the baseline level after about 80–90 ms.

All neurons showed spatial frequency selectivity, responding selectively to either very low spatial frequencies, with preferred spatial frequencies below 0.01 cpd (e.g., Fig. 1B, unit 2) or, as for most units, to preferred spatial frequencies between 0.01 and 0.1 cpd (e.g., Fig. 1, A and C, units 1 and 3).

Nonetheless, these tuning curves changed substantially over time. For two of the representative cells [units 1 and 2 (Figs. 1A, 1B, 3A, and 3D)], the preferred spatial frequency was not constant, but increased over time. Figure 1B (unit 2) shows that the unit initially was tuned at τ = 34 ms to a very low spatial frequency (maximal response at an f_pk of 0.0025 cpd). Over time, the spatial frequency with maximal response strength f_pk shifted to 0.0085 cpd at τ = 82 ms.

Fig. 3.

A, D, and G: temporal analysis of the same units as those in Fig. 1, A–C: heat plot of the response to different spatial frequencies as a function of different delay times τ. Warmer colors indicate response enhancement; colder colors indicate response suppression. B, E, and H: preferred spatial frequency f_pk as a function of the time delay τ, between τ_dev and τ_decay. cpd, Cycles/degree. C, F, and I: quality factor Q in function of time delay τ, between τ_dev and τ_decay.

This shift in f_pk was more clearly illustrated in Fig. 3, D and E, where we plotted f_pk as a function of time delay τ between τ_dev and τ_decay (see Fig. 2 for definitions of these time points). The total shift of f_pk during this period was 2.87 octaves. Another unit (unit 1, Figs. 1A, 3A, and 3B) was tuned to a higher preferred spatial frequency, and the preferred frequency also shifted over time. However, the shift was less pronounced, with f_pk changing from 0.0278 to 0.0378 cpd between delay times τ of 24 and 64 ms, resulting in a shift of 0.56 octaves between τ_dev and τ_decay.

For both of these units, selectivity did not clearly increase over time (Fig. 3, A and D). The responses for spatial frequencies below f_pk visibly decreased at later delay times, but these responses were not obviously suppressed below baseline unlike in macaque monkeys (Bredfeldt and Ringach 2002). Some response suppression below baseline was present in these units, but, in general, this amounted to an overall decrease in response at all or most spatial frequencies. In addition, it only occurred after the excitatory response again had reached baseline levels for all spatial frequencies (Figs. 1 and 3). Another unit (unit 3, Figs. 1C, 3G, and 3H) was tuned to a similar preferred spatial frequency as unit 1, but the tuning curve for this cell remained stable at all delays, with no observable shift in f_pk over time. Also here, selectivity did not change over time, neither was there increased response suppression at low spatial frequencies, except at very late τ.

Population Data of Spatial Frequency Tuning

Preferred spatial frequency.

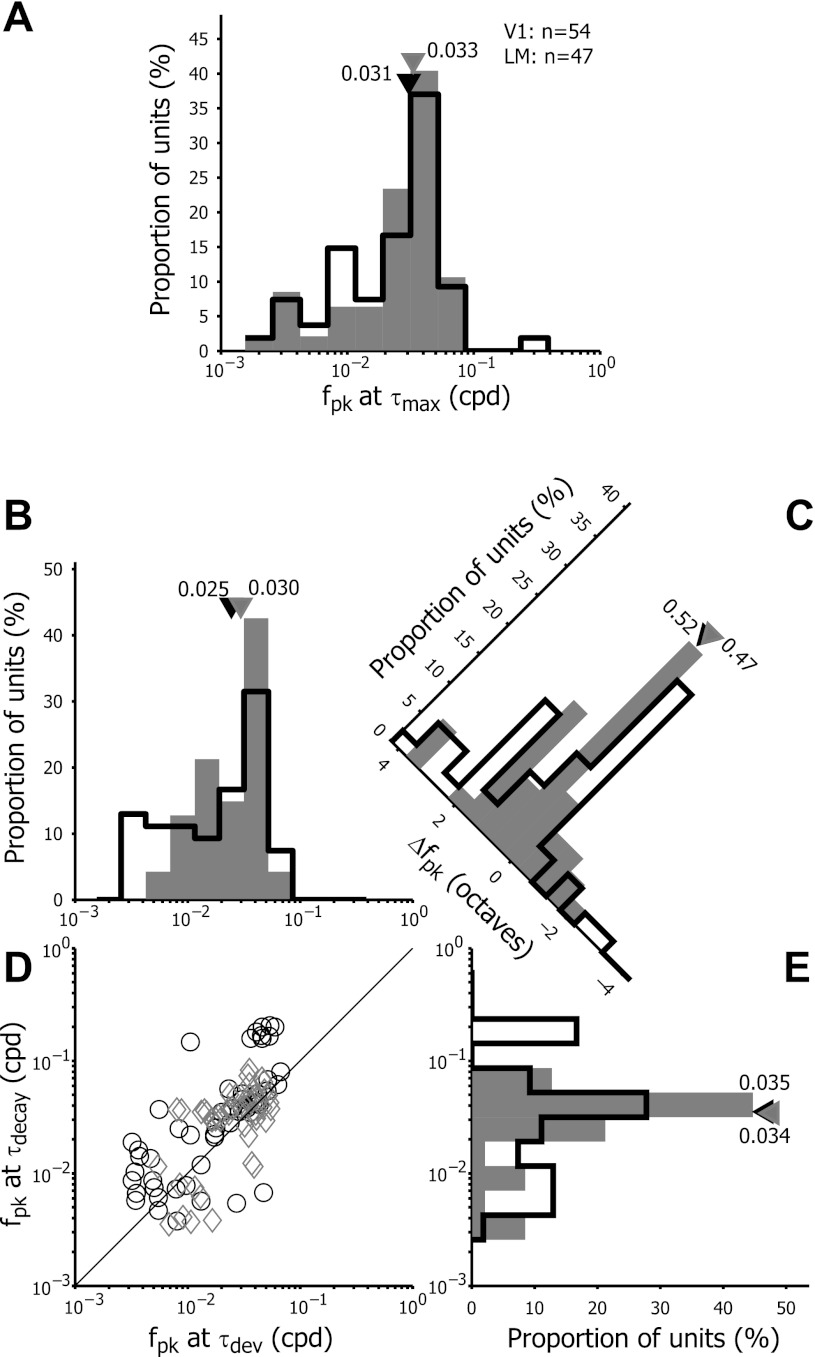
We measured the preferred spatial frequency (f_pk) from R(f,τ_max) for both V1 and LM neurons. The distribution of the f_pk at τ_max is shown in Fig. 4A. For most V1 and LM neurons, the f_pk ranged from 0.0025 to 0.06 cpd with some LM neurons reaching an f_pk at or above 0.1 cpd. The median f_pk at τ_max for V1 (0.031 cpd) was not significantly different from LM (0.033 cpd) (Wilcoxon sign rank test; P = 0.96).

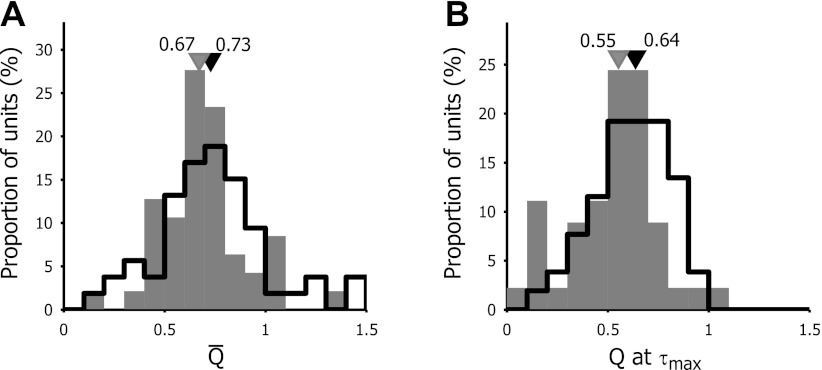
Fig. 4.

Frequency distribution of preferred spatial frequencies f_pk at τ_max (A). The distribution is given for both primary visual cortex (V1, open bars) and lateromedial (LM) neurons (filled bars). The black and gray triangles illustrate the median values of f_pk at τ_max for V1 and LM, respectively. Shift of f_pk over the response duration in V1 (open bars) and LM (filled bars) (B–E). B and E: frequency distributions of f_pk at τ_dev and τ_decay. D: scatter plot of f_pk measured at τ_dev vs. τ_decay. Black circles depict V1 neurons, and gray diamonds depict LM units. The solid line indicates the unit line, where f_pk at τ_dev is equal to f_pk at τ_decay. C: frequency distribution of the difference in f_pk between τ_decay and τ_dev (Δf_pk). Triangles indicate median values of the population data.

To characterize the temporal dynamics of f_pk, we measured the Δf_pk, the difference in f_pk at τ_decay and τ_dev. Figure 4, B–D, shows the distribution of Δf_pk for the V1 and LM cell populations. The scatter plot illustrates that the majority of the V1 and LM cells had higher preferred spatial frequencies at τ_decay than at τ_dev; they lie above the unity line. The histogram shows the distribution of Δf_pk across the population of neurons. Positive values of Δf_pk indicate that f_pk shifted from lower to higher spatial frequencies between τ_dev and τ_decay. Negative values correspond with decreased preferred spatial frequencies over the response delay. On average, f_pk changed positively (with average Δf_pk = 0.85 octaves in V1 and 0.61 octaves in LM), which is in the same range as the shifts observed in monkey V1 (Bredfeldt and Ringach 2002). The median values showed positive Δf_pk values as well (median Δf_pk = 0.52 octaves in V1, 0.47 octaves in LM), and most units had a higher preferred spatial frequency at τ_decay than at τ_dev (Paired Wilcoxon sign rank test, V1: P < 0.0001, LM: P = 0.02019). We did not observe statistically significant differences in the changes of f_pk over time between V1 and LM neurons (Wilcoxon sign rank test, P = 0.57).

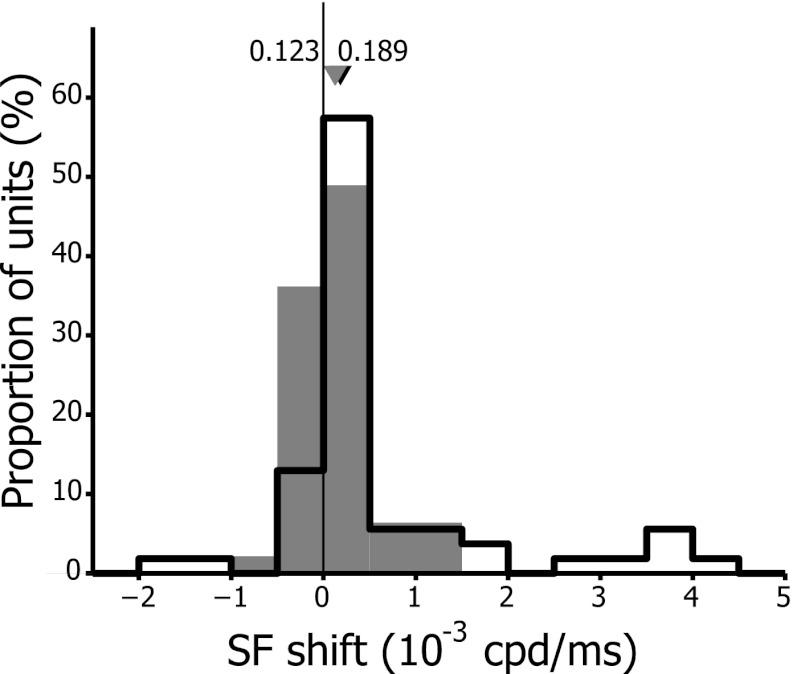
Because the observed changes in f_pk were subtle and based on only two time points, we also determined the rate of change of the preferred spatial frequency. For each neuron, we plotted f_pk vs. τ and fit a line to the f_pk values lying between τ_dev and τ_decay. The distribution of the slopes, which provides the rate and direction of change of f_pk in V1 and LM, is shown in Fig. 5. Eighty-three percent (45/54) of the cells in V1 and 62% (27/48) of those in LM displayed earlier response latencies to low spatial frequencies while response latencies for higher spatial frequencies occurred later. The median slope was significantly different from zero in V1 (Wilcoxon sign rank test, P < 0.0001) while, although the same trend was visible, it was only close to significance in LM (Wilcoxon sign rank test, P = 0.0704). In contrast to what we observed for Δf_pk, there was a significantly higher median rate of change in V1 than in LM (V1: 0.189 × 10⁻³ cpd/ms, LM: 0.123 × 10⁻³ cpd/ms, Wilcoxon rank sum test, P = 0.0401). Mean rates of change were 0.69 × 10⁻³ cpd/ms in V1 and 0.13 × 10⁻³ cpd/ms in LM.

Fig. 5.

Distribution of optimal spatial frequency (SF) rate of change in V1 (open bars) and LM (filled bars). Rates of change were obtained from the slope of the line fitted to the plot of f_pk vs. τ between τ_dev and τ_decay. Positive values indicate increasing f_pk over time, and negative values reflect decreasing f_pk. Black and gray triangles correspond to median values of the rate of change for the population of V1 and LM cells, respectively.

These results demonstrate that, as in V1 of macaque monkeys and cats and even the wulst of burrowing owl, there is an observable shift in optimal preferred spatial frequency over time, indicating that at least some level of spatiotemporal inseparability is present in mouse visual cortex, especially at the level of the primary visual cortex.

Spatial frequency selectivity.

In macaque monkey, the shift in preferred spatial frequency over time is accompanied by an increase in spatial frequency tuning selectivity (Bredfeldt and Ringach 2002). To analyze whether the origin of the temporal increase in f_pk of mouse visual cortex neurons is similar to that in macaque monkeys, we next analyzed the selectivity of spatial frequency tuning over time. To directly compare with the previously published data in macaque monkeys by Bredfeld and Ringach, we used the Q-factor, the ratio of the peak spatial frequency over the difference between low and high cut-off frequencies, as a measure to estimate the spatial frequency tuning selectivity.

We measured the Q-factor for both R(f,τ_max) and the time-averaged tuning curve R̄(f). The selectivity was significantly higher for the mean tuning curve than at τ_max, both in V1 and LM (Wilcoxon sign rank test, V1: P = 0.0130; LM: P = 0.0009). This was observed in monkey V1 as well (Bredfeldt and Ringach 2002). Figure 6 shows the distribution of the Q-factor of the time-averaged tuning curves and the tuning curve at τ_max for V1 and LM. For the mean tuning curve, the median selectivity was 0.73 for V1 neurons and 0.67 for LM neurons (Wilcoxon sign rank test: P = 0.3302), ranging from barely tuned (Q-factor of mean tuning curve = 0.11) to highly tuned [Q-factor R̄(f) = 2.03]. At τ_max, selectivity was significantly higher in V1 than in LM (Wilcoxon sign rank test: P = 0.0379, V1: median Q = 0.64; LM: median Q = 0.55).

Fig. 6.

Frequency distribution of the Q-factor for the average response tuning curve (A) and the response tuning curve at τ_max (B). The Q-factor, as a measure of selectivity, corresponds to the ratio of f_pk over the difference between f_high and f_low, at delay τ. Open bars represent V1 neurons, and filled bars represent LM neurons. Black and gray triangles indicate the median values of Q for the population of V1 and LM cells, respectively.

The representative cells shown in Figs. 1 and 3 demonstrated that, in these units, the Q-factor did not change much over time (Fig. 3, C, F, and I). Also, ΔQ (the difference between the Q-factor at τ_dev and τ_decay) were very close to zero. To determine if the selectivity was unchanged for the cell population, we plotted the Q-factor at τ_dev and τ_decay (Fig. 7, A–D) for each unit. There was no trend toward an increase in spatial frequency selectivity over time for these neurons unlike in monkey V1. To the contrary, in the scatter plot, cells were located both above and below the unity line, and ΔQ values were distributed around zero. Most of the units did not show a large time-dependent change in selectivity, and, for cells whose selectivity changed, this change could go both toward a decrease or an increase in selectivity, resulting in the absence of significant net changes in selectivity (Wilcoxon paired sign rank test: V1: P = 0.6115; LM: P = 0.6036). We also did not observe differences in the distribution of ΔQ between V1 and LM neurons.

Fig. 7.

Analysis of the temporal dynamics of selectivity Q in V1 (open bars) and LM (filled bars). A and D: frequency distributions of Q at τ_dev and τ_decay. C: scatter plot of Q measured at τ_dev vs. τ_decay. Black circles depict V1 neurons, and gray diamonds depict LM units. The solid line indicates the unit line, where Q at τ_dev is equal to Q at τ_decay. B: frequency distribution of the difference in Q between τ_decay and τ_dev (ΔQ). E and F: frequency distribution of the change in selectivity (ΔQ) over the time course of the response, separately plotted for units with a decrease in f_pk over time (Δf_pk ≤ 0; E) or for units with an increase in f_pk over time (Δf_pk > 0; F). Triangles indicate median values of the population data.

This apparent lack of a clear increase in tuning selectivity in mouse visual cortex neurons is contrary to what has been observed in macaque monkeys (e.g., Bredfeldt and Ringach 2002). In macaque monkeys, the increased preferred spatial frequency over time was shown to be related to an increase in tuning selectivity. Because there is also a minority of mouse units that showed a time-dependent decrease in f_pk (see Fig. 4C) and thus have negative Δf_pk values, we asked whether there is a correlation between the direction of changes in f_pk and the changes in selectivity. We separately plotted the distribution of ΔQ for units with a negative Δf_pk and for those with a positive Δf_pk (Fig. 7, E and F). We would expect that, if the increase in f_pk depended on increased selectivity, the ΔQ for units with a positive Δf_pk would be positive as well, whereas the ΔQ for units with a time-dependent decrease of f_pk would be negative. However, we found that both for units with negative as well as positive Δf_pk, the ΔQ was distributed around zero with an equal distribution to positive and negative ΔQ values. This was the case in both V1 and LM (Wilcoxon paired sign rank test: V1, Δf_pk ≤ 0: P = 0.8603; V1, Δf_pk > 0: P = 0.7416; LM, Δf_pk ≤ 0: P = 0.8457; LM, Δf_pk > 0: P = 0.5911).

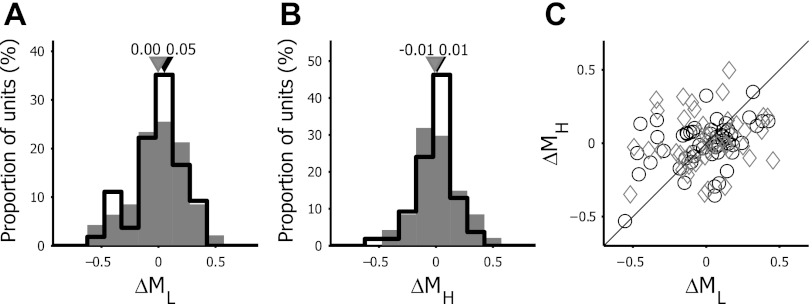
An alternative way to look at changes in selectivity is to analyze time-dependent changes in the steepness of the flanks of the tuning curves. Figure 8 illustrates the distribution of the changes in steepness between τ_dev and τ_decay for the limbs of the tuning curve below (ΔM_L) and above (ΔM_H) the f_pk. Both ΔM_L and ΔM_H were distributed around zero, and the shape of their distribution histogram was similar as well, indicating that there is no bias to changed tuning curve steepness at either side of f_pk. This was in contrast to the increased curve steepness below f_pk and the unchanged steepness above f_pk in monkey (Bredfeldt and Ringach 2002). This was not surprising given the lack of changes in selectivity in mouse neurons that would occur when the steepness of the tuning curve would change over time (e.g., Bredfeldt and Ringach 2002 and Fig. 4D). There were no statistical differences between V1 and LM for these parameters.

Fig. 8.

Temporal dynamics of steepness in tuning curves. A: frequency distribution of the change in steepness between τ_dev and τ_decay for the part of the tuning curve below f_pk [M_L = f_low/f_pk, ΔM_L = M_L(τ_decay) − M_L(τ_dev)]. B: frequency distribution of the change in steepness between τ_dev and τ_decay for the part of the tuning curve above f_pk [M_H = f_pk/f_high, ΔM_H = M_H(τ_decay) − M_H(τ_dev)]. Open bars indicate V1 neurons, and filled bars represent LM neurons. Black and gray triangles depict the median values of V1 and LM neurons, respectively. C: scatter plot of the temporal change in steepness of the low vs. high spatial frequency segment of the tuning curves. Black circles indicate V1 neurons, and gray diamonds correspond to LM neurons. The black line illustrates the unity line where ΔM_L and ΔM_H are equal. Positive values of ΔM_L and ΔM_H indicate that the corresponding side of the tuning curve becomes steeper over time, whereas negative values represent a decrease in steepness.

Both the Q-factor and the steepness of the tuning curve flanks provide a selectivity measure that is limited to the central part of the curve. To obtain a more global selectivity measure that also could act as a time-dependent measure for the suppression of the response to spatial frequencies below f_pk, we calculated the difference in low spatial frequency suppression between τ_decay and τ_dev (ΔLSFS). As a control, we also calculated the difference in high spatial frequency suppression (ΔHSFS) to analyze possible suppression of the response at spatial frequencies higher than f_pk. Figure 9, A and B, shows the distribution for both ΔLSFS and ΔHSFS for V1 and LM neurons. From the distribution of ΔLSFS, there was a marked reduction in the response to the lowest spatial frequency tested in this study compared with the response at f_pk. For V1, the median ΔLSFS was −0.08, with the LSFS at τ_decay and τ_dev significantly different (Wilcoxon paired sign rank test: P = 0.0036). In LM, ΔLSFS did not differ significantly from zero (median ΔLSFS = −0.03, Wilcoxon paired sign rank test for LSFS at τ_decay and τ_dev: P = 0.7491). This showed that, at least in V1, the response to the lowest extreme of tested spatial frequencies was markedly suppressed between τ_dev and τ_decay. In contrast, high spatial frequency responses were markedly less suppressed at τ_decay than at τ_dev in V1 (median ΔHSFS = 0.13, Wilcoxon paired sign rank test for HSFS at τ_decay and τ_dev: P < 0.0001). Again, in LM, there was no difference between HSFS at τ_decay and τ_dev (Wilcoxon paired sign rank test: P = 0.7973; median ΔHSFS = 0.002).

Fig. 9.

Frequency distributions of the temporal shift in low spatial frequency suppression (LSFS, the response for the lowest spatial frequency over the response to f_pk, A) and high spatial frequency suppression (HSFS, the response for the highest spatial frequency over the response to f_pk, B) between τ_dev and τ_decay for V1 (open bars) and LM (filled bars) neurons. C and D: frequency distribution of the change in LSFS (ΔLSFS) over the time course of the response, separately plotted for units with a decrease in f_pk over time (Δf_pk ≤ 0; C) or for units with an increase in f_pk over time (Δf_pk > 0; D). Triangles indicate median values of the population data (black: V1, gray: LM).

We separately plotted the ΔLSFS values for neurons with a decrease (Fig. 9C) and an increase (Fig. 9D) in the preferred spatial frequency over time. In V1, only for neurons with a positive Δf_pk value, we could detect a significant increase in response suppression to the lowest spatial frequency (median ΔLSFS = −0.11, Wilcoxon paired sign rank test for LSFS at τ_decay and τ_dev: P = 0.0030). For units with a negative Δf_pk, or all units in LM, there were no significant deviations of ΔLSFS from zero.

Suppression.

In monkeys, the increase in selectivity of the spatial frequency tuning curve over time was often accompanied by significant response suppression below the baseline for the spatial frequencies below the optimal (Bredfeldt and Ringach 2002). Indeed, Malone and Ringach (2008) demonstrated that inseparability was highest when enhancement and suppression were of roughly equivalent magnitude and that, when responses were dominated by enhancement without much suppression, the separability index was highest.

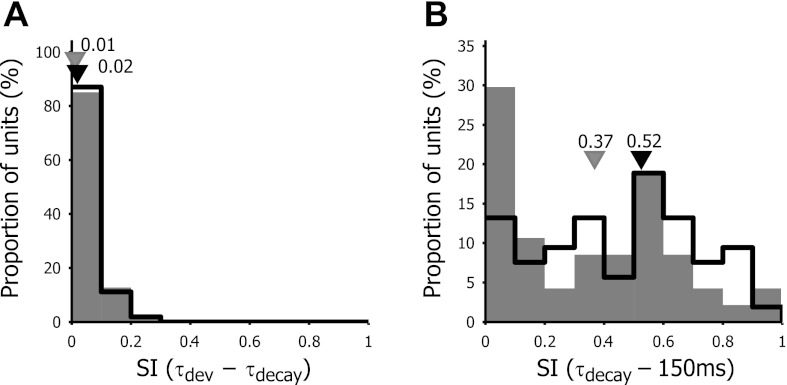
Response suppression below the baseline was therefore quantified by calculating the suppression index, the relative contribution of the suppression to the overall response. A value of 1.0 indicates that the response is purely suppressive; a value of 0 indicates complete absence of suppression; and a suppression index of 0.5 signifies that enhancement and suppression equally contribute to the response. While in monkey 69% of the units with significant suppression had a mean suppression index of 0.27 (Bredfeld and Ringach, 2002), we did not detect significant suppression during the response development between τ_dev and τ_decay. The mean suppression index in V1 was 0.02 ± 0.05 and amounted to 0.01 ± 0.06 in LM (Fig. 10A).

Fig. 10.

Frequency distribution of the suppression index (SI) for time delays τ_dev to τ_decay (A) and for delays from τ_decay to τ = 150 ms (B). V1 neurons are represented by open bars and LM neurons by filled bars. Black and gray triangles depict the median values of V1 and LM neurons, respectively.

Nevertheless, as shown by the representative cells in Fig. 1 as well as the minimum and maximum responses in Fig. 2B, about one-third of the units displayed suppression after the response had returned to baseline levels. Often, this suppressive phase encompassed all spatial frequencies tested. To quantify this general suppressive effect, we calculated the suppression index from τ_decay up to a delay of 150 ms (Fig. 10B). We observed strong suppression, with a mean suppression index for V1 of 0.46 ± 0.25 and 0.35 ± 28 in LM. There was a significant difference in suppression index between V1 and LM (Wilcoxon sign rank test: P = 0.0491).

DISCUSSION

The main finding of this study was that the spatial frequency tuning in mouse visual cortex was dynamic in the temporal domain. For the majority of neurons, the preferred spatial frequency was shifted toward higher spatial frequencies over the duration of their response. This shift in the preferred spatial frequency was not accompanied by an increase in tuning curve selectivity over time. Nevertheless, the response to the lowest spatial frequencies decreased over a short period of time relative to the response of the preferred spatial frequency. Also, there was no suppression below baseline levels. Instead, suppression only emerged after the tuning curve had returned to baseline levels. Another key finding was that there were no clear differences in inseparability of spatial frequency and time for the tuning curves for neurons in V1 and extrastriate region LM.

Temporal Shift of Preferred Spatial Frequency

The preferred spatial frequency measured in mice using the dynamic gratings and reverse-correlation method was rather low (around 0.031 cpd at τ_max) compared with that of cat and monkey. However, it is very much in line with the preferred spatial frequency of mouse V1 neurons that was determined with drifting sinusoidal gratings. Recent studies established the median optimal spatial frequency in mouse V1 as being in the range from 0.03 cpd (Gao et al. 2010) and 0.032 cpd (Niell and Stryker 2008) to 0.04 cpd (Van den Bergh et al. 2010). Also in LM this corresponds with the data found in the literature [0.033 vs. 0.04 cpd in V2L (Van den Bergh et al. 2010) and 0.028 cpd in LM (Marshel et al. 2011)].

As in cats and monkeys, the majority of V1 and LM neurons developed a time-dependent increase in the optimal spatial frequency. This shift in the peak spatial frequency of the tuning curves was qualitatively similar to that observed in earlier studies in monkeys (Bredfeldt and Ringach 2002; Frazor et al. 2004; Mazer et al. 2002) and cats (Frazor et al. 2004; Nishimoto et al. 2005). Importantly, the time-dependent shift in mice was comparable when quantified in octaves, which compensates for the much lower quality of vision in mice.

We were able to compare the magnitude of the shift in preferred spatial frequency with that estimated in Bredfeldt and Ringach (2002), since we employed essentially the same experimental paradigm and analysis methods as in their study. The only difference between the two studies was that we defined the delays of beginning and end of the response as τ_dev and τ_decay, respectively, instead of τ_onset and τ_offset. We decided on these delay times since τ_onset and τ_offset, which are based on temporal variation in the tuning curve, were not clearly defined for several of the cells in our database, which had somewhat more variable responses for τ < 30 ms. Because τ_dev and τ_decay are by definition the delays where the response reaches half-maximal values in contrast to τ_onset and τ_offset that delimit the beginning and end of the visual response, the total response time over which Δf_pk was calculated was somewhat smaller than reported by Bredfeldt and Ringach (2002). Therefore, our procedure could result in a modest underestimation of the magnitude of change in f_pk compared with that reported in monkeys. Nevertheless, the average shift in f_pk of 0.85 octaves we observed in mouse V1 was similar but slightly higher than the value reported for monkeys (0.62 octaves).

Using a similar method, Mazer et al. (2002) detected only a small but significant shift in f_pk in monkeys, which they did not quantify. They found that most cells had a positive rate of change of preferred spatial frequency over the response. Because they reported this rate of change as absolute values, we cannot make direct comparisons between mouse and monkey partly because of much lower acuity in mice. Nevertheless, the relative rate of the spatial frequency shift was similar in mouse V1, but less so compared with LM. Frazor et al. (2004), on the other hand, found a similar shift in f_pk in cats (0.88 octaves) and monkeys (0.97 octaves), although they employed a markedly distinct method; 200-ms static gratings were shown with short interstimulus intervals, and then they analyzed the peristimulus time histograms across different spatial frequencies. This procedure eliminated potential overlap in the response across different stimuli. In another study with a reverse-correlation method to perform subspace mapping of the RFs in cats, the spatial frequency shift was visible (Nishimoto et al. 2005). The shift in f_pk was analyzed both in area 17 and area 18, and the magnitude of the shift was somewhat smaller than in mouse: 0.22 and 0.24 octaves, respectively.

As in monkeys and cats, neurons in mouse visual cortex prefer coarser stimuli early during their response while finer stimuli preferentially elicit responses at a later time (Marr and Poggio 1979; Menz and Freeman 2004). As such, this temporal shift in spatial frequency preference (coarse-to-fine processing) might be a common property of visual cortex neurons of many mammals, even in those lacking orientation columns or having “low-quality” vision.

Putative Mechanisms for Spatial Frequency Dynamics

One of the most obvious differences between our results and those from monkeys was that we did not observe a time-dependent increase in the selectivity of the tuning curves in mouse. In monkeys, the change in the local selectivity measure over the response time (as estimated by ΔQ) was positive for nearly all units, indicating a temporal increase in the sharpness of the tuning curves (Bredfeldt and Ringach 2002). Moreover, these investigators observed a rising steepness of the tuning curve over time below the peak spatial frequency and a time-dependent increase in suppression of the responses to lower spatial frequencies below baseline levels. These investigators concluded that the lagged suppression to low spatial frequency first sharpens the tuning curve and that, when the magnitude of the suppression increases relative to the magnitude of excitation, the increasing overlap of excitation and inhibition pushes the peak of the spatial frequency tuning curve toward higher frequencies (Bredfeldt and Ringach 2002). The absence of a local selectivity increase and a rise in the steepness of the tuning curve for the low spatial frequencies close to the preferred frequency in mice suggest that different mechanisms could be operating in mice for the observed dynamics of spatial frequency tuning.

An alternative explanation for the observed shift in peak spatial frequency in V1 considers the differences in the response properties of magnocellular (M) and parvocellular (P) neurons in the LGN. This feedforward model states that convergent input from M cells that fire faster than P cells but have RFs with twice the size than those of P cells could account for the latency differences as a function of spatial frequency in V1 (Frazor et al. 2004; Mazer et al. 2002). Because slow-conducting X and fast-conducting Y cells within cat LGN also provide inputs to area 17 differing in response latency that covaries with spatial frequency, this model could explain the observed dynamics of spatial frequency tuning in cat as well (Nishimoto et al. 2005). Although in mice no distinction between M and P, or X and Y LGN neurons has yet been established (Grubb and Thompson 2003; Huberman and Niell 2011), there are V1 neurons in mice with low spatial resolutions that prefer higher temporal frequencies while cells with high spatial resolutions prefer slowly moving stimuli, supporting the notion of “parallel” input channels into V1 (Gao et al. 2010). In one highly visual rodent, the squirrel, such parallel processing in LGN has been observed, with short-latency neurons having lower spatial resolution than longer-latency neurons (Van Hooser et al. 2003). This suggests that such parallel input into V1 might be a general feature of the visual system of rodents, and that of mice.

The key observation in our study that supports the above feedforward model comes from our analysis of tuning curve selectivity with a global selectivity measure, i.e., the LSFS (Xing et al. 2004). Here, we found, at least in V1, a small but significant increase in tuning curve selectivity due to a substantial reduction in response rates to the lowest spatial frequencies (Fig. 9). In the burrowing owl wulst, this shift in LSFS was also observed although it was accompanied by a decrease in tuning bandwidth but not by a change in the preferred spatial frequency (Pinto and Baron 2010). We did not analyze tuning bandwidth, since we knew from earlier studies that up to 30% of mouse units showed low pass tuning for spatial frequency (Van den Bergh et al. 2010) and would thus provide no useful metric for this property.

Another explanation for the shift in optimal spatial frequency in V1 was suggested by Allen and Freeman (2006). They demonstrated that spatial frequency tuning dynamics are present in the LGN and that a feedforward model could explain the observed dynamics at the cortical level. Because similar dynamics of spatial frequency tunings have not been studied in the mouse LGN, it is not possible to determine how much of what we observed in mouse V1 and LM can be explained by similar retinogeniculate mechanisms in the mouse visual system. However, despite similar shifts in optimal spatial frequency, the rate of change was lower in LM than in V1, suggesting that, apart from direct LGN input, at least some additional processing within cortex is required to observe these differences between cortical areas.

Suppression and Differences Between V1 and LM

It is unclear why we did not observe strong suppression for the lower spatial frequencies as reported in monkeys (Bredfeldt and Ringach 2002). We used a nearly identical reverse-correlation method where interleaved blank gray frames of average luminance were used to assess baseline responses. This allowed us to observe suppression of responses below the baseline after the excitatory responses had disappeared (Fig. 10B). However, we could not demonstrate strong suppressive effects while the excitatory response was still present (Fig. 10A) although we sporadically found neurons with weak suppression of spatial frequencies below the peak, concomitant with the excitatory response.

One possible explanation for the apparent lack of the “tuned suppression” in mouse V1 could be the use of urethane as an anesthetic/analgesic. Urethane tends to depress spontaneous and visually evoked cortical responses in rodents (e.g., Girman et al. 1999; Sceniak and Maciver 2006) although it is known to have little or no effect on the neurons' excitatory or inhibitory synaptic inputs (Sceniak and Maciver 2006). Because the general loss of cell's excitability occurs to the same degree in GABAergic and glutamatergic neurons, the use of urethane is unlikely to influence the excitation/inhibition balance. On the other hand, one of the significant consequences of reduced excitability, whether urethane induced or not, is an impoverished signal-to-noise ratio (SNR) of responses in mouse V1 neurons. If SNR in mouse V1 is substantially lower than that in macaque V1, the suppression for low spatial frequency could be “masked” or not readily “visible.” The visually evoked responses in mice V1 tend to be lower than those in macaque V1 while the maintained discharge is higher in mice (Niell and Stryker 2008; Van den Bergh et al. 2010). This means that “suppression” could be more easily demonstrated in mice, and the variability of visually evoked spiking (fano factor) should be less in mice. Therefore, a potentially lower SNR in mouse V1 may not adequately explain the apparent absence of tuned suppression for low-spatial-frequency stimuli.

In this regard, the question remains as to why there is a global suppressive effect in mouse V1 only beyond the decay of the excitatory response with no local suppression of low spatial frequencies. One possibility is that, in mouse visual cortex, the response level for low spatial frequencies can still decrease due to weaker suppression, potentially giving rise to a small increase in preferred spatial frequency, but without reducing responses below baseline levels. Moreover, suppression of responses below the baseline might be “unmasked” only when the excitatory responses have already returned close to baseline levels. As a result, more global suppression at the end of the excitatory response emerges (Fig. 2). The broad tuning of the suppression at late time can arise from the broad tuning for spatial frequency found in mouse GABAergic neurons (Kerlin et al. 2010).

Related to these observations, we found differences in the strength of the late suppressive effect following the disappearance of the excitatory response between V1 and LM. In fact, this was one of the few clear-cut differences between the two visual areas in the diverse temporal properties of spatial frequency tuning we investigated. Our results did not show differences in the magnitude of the shift in preferred spatial frequency between V1 and LM. Similarly, Nishimoto et al. (2005) did not detect differences in the dynamics of the preferred spatial frequency between cat area 17 and 18.

An important question here would be why the delayed suppression we observed is stronger in V1 than in LM. We have previously found that RF surround suppression is stronger in V1 than in V2L. Moreover, the surround suppression in mouse V1 is significantly weaker than that observed in macaque V1 (Van den Bergh et al. 2010). Because surround suppression and the suppressive effects observed in the dynamics of spatial frequency tuning are likely to be supported by inhibitory cortical neurons (Angelucci et al. 2002; Bair et al. 2003; Bredfeldt and Ringach 2002), our data suggest that the general level of inhibition, either intracortical or as feedback from higher visual areas, is likely to be lower in LM than in V1. A relatively lower level of inhibition in mice vs. monkeys might be closely associated with the observed differences in the dynamics of spatial frequency tuning between the two species. Also, the difference between the “delayed” suppression in mouse V1 and LM suggests that the mechanism for this suppression occurs within these respective visual areas and does not originate from brain regions earlier in the visual pathway, such as the geniculate nucleus (e.g., Allen and Freeman 2006).

In this study, we demonstrated that, in mouse visual cortex, neurons display a time-dependent increase in preferred spatial frequency. The observed dynamics of spatial frequency tuning did not result from a significant increase of selectivity due to strong suppression of responses for low spatial frequencies as in macaque monkeys (Bredfeldt and Ringach 2002) but rather by a more subtle decrease in the response for low spatial frequencies. This temporal spatial frequency change in mice appears to be closely associated with weak suppression tuned to lower spatial frequency and/or the parallel feedforward input streams from the LGN that have shorter latencies for cells tuned toward lower spatial frequencies and longer latencies for neurons tuned to higher spatial frequencies. Taken together, our results suggest that there are subtle but significant differences between mice and macaque monkeys with respect to the cortical mechanisms underlying the dynamics of spatial frequency tuning of individual neurons.

GRANTS

This work was supported by grants of the Fund for Scientific Research-Flanders (FWO-Vlaanderen) (G.0434.08N to G. Van den Bergh and L. Arckens), the Research Council of the K.U.Leuven (OT 09/22 to L. Arckens), and the National Eye Institute (R01 EY-008128 and P30 EY-007551 to Y. M. Chino).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

Author contributions: S.V., B.Z., Y.M.C., and G.V.d.B. conception and design of research; S.V. and G.V.d.B. performed experiments; S.V. and G.V.d.B. analyzed data; S.V., B.Z., Y.M.C., L.A., and G.V.d.B. interpreted results of experiments; S.V. and G.V.d.B. prepared figures; S.V., B.Z., L.A., and G.V.d.B. drafted manuscript; S.V., B.Z., Y.M.C., L.A., and G.V.d.B. approved final version of manuscript; B.Z., Y.M.C., L.A., and G.V.d.B. edited and revised manuscript.