TwinMARM: Two-stage Multiscale Adaptive Regression Methods for Twin Neuroimaging Data

Abstract

Twin imaging studies have been valuable for understanding the relative contribution of the environment and genes on brain structures and their functions. Conventional analyses of twin imaging data include three sequential steps: spatially smoothing imaging data, independently fitting a structural equation model at each voxel, and finally correcting for multiple comparisons. However, conventional analyses are limited due to the same amount of smoothing throughout the whole image, the arbitrary choice of smoothing extent, and the decreased power in detecting environmental and genetic effects introduced by smoothing raw images. The goal of this article is to develop a two-stage multiscale adaptive regression method (TwinMARM) for spatial and adaptive analysis of twin neuroimaging and behavioral data. The first stage is to establish the relationship between twin imaging data and a set of covariates of interest, such as age and gender. The second stage is to disentangle the environmental and genetic influences on brain structures and their functions. In each stage, TwinMARM employs hierarchically nested spheres with increasing radii at each location and then captures spatial dependence among imaging observations via consecutively connected spheres across all voxels. Simulation studies show that our TwinMARM significantly outperforms conventional analyses of twin imaging data. Finally, we use our method to detect statistically significant effects of genetic and environmental variations on white matter structures in a neonatal twin study.

1 Introduction

The typical design of a twin study compares the similarity of monozygotic twins (MZ), who share the same genetic polymorphisms, to that of dizygotic twins (DZ), who share an average of 50% of their genetic polymorphisms. Under the equal environment assumption across zygosities, the known differences in genetic similarity allows us to dissect the effects of genes and environment on a known phenotype, such as total brain volume and volumes of subcortical structures. Thus, twin neuroimaging studies have been a valuable source of information for evaluating the inheritance of brain structure and function by disentangling genetic factors from environment [1, 2, 3, 4, 5, 6, 7, 8]. For instance, high heritability was found in different brain volumes including intracranial volume, total brain volume, and global gray and white matter volumes [9, 3, 10]. Moreover, cortical thickness in the sensorimotor cortex, middle frontal cortex, and anterior temporal cortex were found to be influenced by genetic factors [5, 11].

The voxel-wise methods for analyzing twin neuroimaging data on a two-dimensional (2D) surface (or in a three-dimensional (3D) volume) are sequentially executed in three steps. The first step is to use standard smoothing methods to spatially smooth the imaging data [5, 6, 7]. These smoothing methods are commonly independent of the imaging data and apply the same amount of smoothing throughout the whole image. See, for example, [12] for overviews of some smoothing methods in the neuroimaging literature. The second step involves fitting statistical models to imaging measures from all twin pairs at each voxel or surface location separately to generate a parametric map of test statistics (or p–values) [13, 14]. The most commonly used models are structural equation models, which primarily decompose the observed phenotypic variance into additive genetic, dominant genetic, common environmental components, and random noise [15, 16]. The third step is to compute adjusted p-values in order to correct for testing multiple hypotheses across thousands to millions of locations using multiple comparison correction methods (e.g., random field theory (RFT), false discovery rate (FDR), or permutation methods)[17, 18, 19, 20, 21, 22].

The existing voxel-wise methods based on Gaussian kernel smoothing and structural equation models have two major limitations for analyzing twin neuroimaging data, which underscore the great need for further methodological development. It is well known that the commonly used Gaussian kernel for smoothing imaging data usually blurs the image data near the edges of the significant regions, which can dramatically increase the numbers of false positives and negatives. As shown in [23, 24], the existing voxel-wise methods can suffer from the arbitrary choice of smoothing extent in the initial smoothing step, which leads to the large number of false positive and false negative results. An overview of different smoothing methods that are used in the neuroimaging literature can be found in [12]. Generally, most methods for smoothing raw twin imaging data take a weighted average of the imaging data at voxels in the neighborhood of each voxel, thus are primarily associated with the mean structure of imaging data. Such a way of smoothing raw twin imaging data can change the variance structure of imaging data, which is primarily associated with genetic and environmental factors [25, 16, 15, 13, 14]. Thus, directly smoothing twin imaging data can introduce substantial bias in estimating these factors and lead to a dramatic increase of the numbers of false positives and negatives. We will investigate the consequence of smoothing twin imaging data by theoretical arguments in the Appendix and using simulated data in Section 3. Recently, [26] examined how the overall significance of voxel-wise effects varied with respect to full width at half maximum(FWHM) of the Gaussian smoothing applied to the fractional anisotropy (FA) images. Their results have shown that raw FAmaps with no smoothing yielded the greatest sensitivity to detect gene effects. Our results give a theoretical justification for their results. In general, directly smoothing raw twin imaging data by using Gaussian kernel should be avoided in practice.

As pointed out by [20] and many others, these voxel-wise methods essentially treat all voxels as independent units in the modeling stage, and they explicitly model the spatial coherence and incorporate the information that spatially contiguous regions of effect with rather sharp edges may exist in neuroimaging data. At least two groups of statistical methods have been developed to characterize spatial dependence in neuroimaging data. The first group of methods is to explicitly incorporate the spatial non-independence in the p-value or testing statistic images. These methods usually combine strength from both the magnitude of testing statistic and cluster extent, where the cluster is defined as the number of contiguous signiificant voxels above a specific threshold [20, 21, 22].

Instead of solely utilizing information in the p-value or testing statistic images, the other group of methods explicitly incorporates the spatial dependence in their models. It is common to use conditional autoregressive (CAR), Markov random field (MRF), and other spatial correlation priors to characterize spatial dependence among spatially connected voxels [27, 28, 29, 30, 31, 32]. In addition, a wealth of image denoising and restoration methods has been developed for pre-processing a single image in the literature. An overview of image denoising and restoration methods has been given in [33, 34] and references therein. For instance, Polzehl et al.[35, 36] developed a propagation separation(PS) approach to adaptively and spatially smooth images from a single image without detecting edge curves/surfaces explicitly. In Qiu et al.[37, 38], novel three-dimensional (3D) denoising procedures were proposed to nonparametrically estimate a 3-D jump surface from noisy data. In Tabelow et al. [39, 40, 41], the original PS idea was adapted to develop a multiscale adaptive linear model to adaptively and spatially denoise functional magnetic resonance imaging (fMRI) and diffusion tensor images (DTI) from a single subject. Under the linear model for fMRI, In Polzehl et al.[42], a structural adaptive segmentation algorithm was developed to integrate the signal detection with noise detection in one procedure. In Li et al.[43], a multiscale adaptive regression model(MARM) was proposed to integrate the PS approach [35, 36] with general statistical modeling at each voxel for spatial and adaptive analysis of neuroimaging data from multiple subjects in various study designs.

The aim of this article is to develop a pipeline, called TwinMARM, for the spatial and adaptive analysis of twin neuroimaging data. TwinMARM integrates adaptive estimation and testing in a single framework. TwinMARM consists of two stages of multiscale adaptive regression models (MARM). Each stage of TwinMARM constructs hierarchical nested neighborhoods with increasing radii at all voxels, adaptively generates weighted quasi-likelihood functions, and efficiently utilizes available information to estimate parameters. Particularly, in the first stage, weighted quasi-likelihood functions are constructed to capture the mean structure of imaging data in order to establish the relationship between twin imaging data and a set of covariates of interest, such as age and gender. Subsequently, in the second stage, a set of new weighted quasi-likelihood functions is built that utilizes the variance structure of imaging data to disentangle relative contributions of environment and genes on brain structures and their functions.

Compared to all existing methods including MARM and PS, we make several major contributions. TwinMARM represents a novel generalization of MARM and PS. Specifically, PS has been primarily used to solely average imaging intensity, which improves the accuracy in estimating the mean structure of imaging data [42, 39, 40, 41], but we are more interested in variance structure of imaging data in Twin studies. One may directly apply MARM to the structural equation model (SEM) described in Section 2, but we have found that it is computationally difficult to directly optimize the weight likelihood function for SEM. Moreover, the existing MARM and PS methods can only smooth all unknown parameters (or a subset of parameters) simultaneously, since the weights used in MARM and PS depend the weighted distance of the whole parameter vectors. However, we cannot estimate the mean and variance structure of twin imaging data simultaneously. At the same time, extending MARM and PS to smoothing individual parameters is an unsolved problem, since it is very difficult to approximate the covariance matrix of the smoothed parameter estimates obtained from MARM and PS. Fortunately, due to the special model structure for twin data, we are able to find a novel approach, which allows us to apply MARM twice to independently smooth the mean and variance structure of twin imaging data. Theoretically, we have shown in the Appendix that our approach is valid asymptotically. TwinMARM slightly increases the amount of computational time in computing parameter estimates and test statistics, whereas it substantially outperforms the voxel-wise approach in increasing the accuracy of parameter estimates and the power of test statistics. Practically, TwinMARM developed here is applicable to different imaging modalities including DTI, fMRI, and MRI among many others. Particularly, TwinMARM gives a solution to the issue raised in [26]. Due to the importance and popularity of twin imaging studies, TwinMARM will have wide and important applications in the analysis of imaging, genetic, and clinical data collected from twin studies.

2 Methods

2.1 Structural Equation Model

Suppose we observe imaging measures and clinical variables from n₁ MZ twin pairs and n₂ = n − n₁ DZ twin pairs. Imaging measures can be volumes of anatomical regions, the shape representation of the surfaces of cortical or subcortical structures, fMRI signals, diffusion tensors, and tensor-derived measures [44, 45, 46, 47, 48, 49, 50, 5, 6, 7, 8]. Clinical variables may include demographic and environmental variables. Specifically, for the j-th subject in the i-th twin pair, we observe an N_V × 1 vector of imaging measures, denoted by Y_ij = {y_ij(v) : v ∈ }, and a k × 1 vector of clinical variables x_ij = (x_ij1, ···, x_ijk)^T for i = 1, ·, n and j = 1, 2, where x_ij1 is commonly set as 1 and and v, respectively, represent a specific brain region and a voxel in 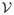. For notational simplicity, we only consider univariate measure.

At a specific voxel v, we consider the structural equation model

$$y_{ij}(v)=x_{ij}^T\mathit{\beta }(v)+a_{ij}(v)+d_{ij}(v)+c_i(v)+e_{ij}(v)$$ (1)

for j = 1, 2 and i = 1, ···, n = n₁ + n₂, where β(v) = (β₁(v), ···, β_k(v))^T is a k × 1 vector representing unknown regression coefficients, a_ij(v), d_ij(v), c_i(v) and e_ij(v) are, respectively, the additive genetic, dominance genetic, common environmental, and residual effects on the i-th twin pair. It is common to assume that a_ij(v), d_ij(v), c_i(v) and e_ij(v) are independently normally distributed with means 0 and variances ${\sigma }_a^2(v),{\sigma }_d^2(v),{\sigma }_c^2(v)$, and ${\sigma }_e^2(v)$, respectively [16, 15, 13, 14, 51]. Moreover, Cov(a_i1(v), a_i2(v)) equals ${\sigma }_a^2(v)$ for MZ twins and ${\sigma }_a^2(v)/2$ for DZ twins, while Cov(d_i1(v), d_i2(v)) equals ${\sigma }_d^2(v)$ for MZ twins and ${\sigma }_d^2(v)/4$ for DZ twins [52]. See a path diagram of model (1) in Figure 1. Due to an identifiability issue, we may not be able to dissect the additive genetic effect, the dominance genetic effect, and the common environmental effect from the residual environmental effect [16, 15, 13, 14]. It is common to consider two simpler models. One is the ACE model, which only includes additive genetic, common environmental, and residual effects. The other is the ADE model, which includes additive and dominance genetic, and residual effects.

Fig. 1.

Diagram for the structural equation model for twin data. The correlation of additive effects (a1, a2) is 1 for MZ twin and 0.5 for DZ twin. The correlation of dominant effects (d1, d2) is 1 for MZ twin and 0.25 for DZ twin. The twin share the same common environmental effect (c). Residual effects (e1, e2) for twin are not correlated.

Without loss of generality, we focus on the ACE model and drop the assumption of normality for a_ij(v), d_ij(v), c_i(v) and e_ij(v) from now on, since TwinMARM is independent of such assumption. For the ACE model, if we are able to estimate all variances $\mathit{\eta }(v)=({\sigma }_a^2(v),{\sigma }_c^2(v),{\sigma }_e^2(v))$, we can disentangle relative contribution of environment and genetic polymorphisms. Specifically, the genetic heritability at voxel v, denoted by g(v), is defined as the ratio of the genetic variance to the total variance of y_ij(v) given by

$$g(v)=\frac{{\sigma }_a^2(v)}{{\sigma }_a^2(v)+{\sigma }_e^2(v)+{\sigma }_c^2(v)}.$$

2.2 TwinMARM

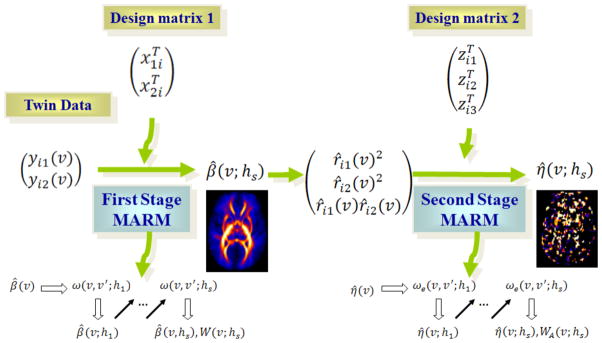
We propose the two-stage multiscale adaptive regression method (TwinMARM) for the analysis of twin imaging data and behavioral data as follows. The first stage is to estimate β = {β(v) : v ∈ }, while the second stage is to estimate η = {η(v) : v ∈ }. In each stage, we reformulate the problem of estimating β (or η) as a regression model and then apply the multiscale adaptive regression model (MARM) in [43], which can be regarded as a generalization of the propogation-seperation (PS) procedure in multiple subjects [35, 53, 36, 39, 40, 41]. The key ideas of MARM and PS are to construct hierarchical nested neighborhoods with increasing radii at all voxels, to adaptively construct weighted quasi-likelihood functions to estimate parameter estimates, and to increase the power of test statistics in detecting subtle changes of brain structures and their functions. A path diagram of TwinMARM is presented in Figure 2.

Fig. 2.

Diagram for the TwinMARM method for twin data. The first stage is to estimate β = {β(v) : v ∈ 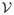}, while the second stage is to estimate η = {η(v) : v ∈ V}. In each stage, we reformulate the problem of estimating β (or η) as a regression model and then apply the multiscale adaptive regression method (MARM) to spatially and adaptively calculate β̂(v;h_s) and η̂(v; h_s) and their associated test statistics. Moreover, y_ij denote imaging measures for twin pairs, x_ij is a vector of clinical variables, β is the vector of unknown regression parameters, r_ij are residuals obtained from first stage, η include the variances of additive genetic, common environmental and residual effects, and z_ij is the design matrix for the second stage. ω(v, v′; h_s) is the weight of the first stage, whereas ω_e(v, v′; h_s) is the weight of the second stage.

2.2.1 TwinMARM: Stage I

The first stage is to estimate β(v) and carry out statistical inference on β(v). Specifically, we consider a bivariate regression model given by

$$Y_i(v)=\left(\begin{array}{c}{y}_{i1}(v)\\ y_{i2}(v)\end{array}\right)={\mathbf{x}}_i^T\mathit{\beta }(v)+{\mathbf{f}}_i(v)=\left(\begin{array}{c}{\mathbf{x}}_i^T\\ {\mathbf{x}}_{i2}^T\end{array}\right)\mathit{\beta }(v)+\left(\begin{array}{c}{f}_{i1}(v)\\ f_{i2}(v)\end{array}\right),$$ (2)

where ${\mathbf{x}}_i=[\begin{array}{cc}{\mathbf{x}}_{i1}& {\mathbf{x}}_{i2}\end{array}]$ and f_i(v) = (f_i1(v), f_i2(v))^T, in which f_ij(v) = a_ij(v) + c_i(v) + e_ij(v) for the ACE model. Although f_i(v) has different covariance structures for MZ and DZ, respectively, we assume that f_i(v) has mean zero and covariance Σ_f (v) for all i to avoid estimating variance components ( ${\sigma }_a^2(v),{\sigma }_c^2(v),{\sigma }_e^2(v)$) in Stage I, which leads a simple procedure for estimating β. We will appropriately account for the misspecification of covariance of f_i(v) in our statistical inference on β(v).

Since all components of β(v) are the parameters of interest and Σ_f (v) can be regarded as nuisance parameters, we first estimate Σ_f (v) across all voxels and then fix them at their estimated values. Specifically, let ℓ(Y_i(v)|x_i, β(v), Σ_f (v)) be the pseudo-likelihood of Y_i(v) given by

$$-0.5log\mid {\mathrm{\Sigma }}_f(v)\mid -0.5{\{Y_i(v)-{\mathbf{x}}_i^T\mathit{\beta }(v)\}}^T{\mathrm{\Sigma }}_f^{-1}(v)\{Y_i(v)-{\mathbf{x}}_i^T\mathit{\beta }(v)\}.$$ (3)

We calculate the maximum pseudo-likelihood estimate of (β(v), Σ_f (v)) given by

$$(\widehat{\mathit{\beta }}(v),{\widehat{\mathrm{\Sigma }}}_f(\widehat{v}))=\underset{(\mathit{\beta }(v),{\mathrm{\Sigma }}_f(v))}{argmax}\ell (Y_i(v)\mid {\mathbf{x}}_i,\mathit{\beta }(v),{\mathrm{\Sigma }}_f(v)).$$ (4)

Let a^⊗2 = aa^T for any vector a and (β̂(v)^(t), Σ̂_f (v)^(t)) be the estimate of (β(v), Σ_f (v)) at the t-th iteration. Computationally, at each voxel v, by setting Σ̂_f (v)⁽⁰⁾ = I₂, a 2 × 2 identity matrix, we iteratively update

$$\begin{array}{l}\widehat{\mathit{\beta }}{(v)}^{(t+1)}={\left\{\sum _{i=1}^n{\mathbf{x}}_i{\widehat{\mathrm{\Sigma }}}_f^{-1}{(v)}^{(t)}{\mathbf{x}}_i^T\right\}}^{-1}\sum _{i=1}^n{\mathbf{x}}_i{\widehat{\mathrm{\Sigma }}}_f^{-1}{(v)}^{(t)}{Y}_i(v),\\ {\widehat{\mathrm{\Sigma }}}_f{(v)}^{(t+1)}={(n-2)}^{-1}\sum _{i=1}^n{\{Y_i(v)-{\mathbf{x}}_i^T\widehat{\mathit{\beta }}{(v)}^{(t+1)}\}}^{\otimes 2}\end{array}$$ (5)

until that the difference between (β̂(v)^(t+1), Σ̂_f (v)^(t+1)) and (β̂(v)^(t), Σ̂_f (v)^(t)) is smaller than a prefixed constant, say 10⁻⁶. From now on, Σ_f (v) will be fixed at Σ̂_f (v) across all voxels v. Statistically, it can be shown that such a substitution has a negligible effect on statistical inference of β.

To estimate β(v) at voxel v, we construct a weighted quasi-likelihood function by utilizing all imaging data in a sphere with radius h at voxel v, denoted by B(v, h). Let ω(v, v′; h) ∈ [0, 1] be a weight function of two voxels and a radius h, which characterizes the similarity between the data in voxels v and v′ such that ∑_{v′∈B(v,h)} ω(v, v′; h) = 1 for all h > 0. If ω(v, v′; h) ≫ 0, it represents that the data in voxels v and v′ are similar to each other, whereas ω(v, v′; h) ≈ 0 indicates that the data in voxel v′ do not contain too much information on β(v). The adaptive weights ω(v, v′; h) play an important role in preventing oversmoothing the estimates of β(v) as well as preserving the edges of significant regions. We utilize all the data {Y_i(v′) : v′ ∈ B(v, h)} to construct the weighted log-likelihood function at voxel v at scale h, which is given by

$${\ell }_{\mathit{obs}}(\mathit{\beta }(v);h)=-0.5\sum _{i=1}^n\sum _{v^{\prime }\in B(v,h)}w(v,v^{\prime };h){\{Y_i(v)-{\mathbf{x}}_i^T\mathit{\beta }(v)\}}^T{\widehat{\mathrm{\Sigma }}}_f^{-1}(v^{\prime })\{Y_i(v)-{\mathbf{x}}_i^T\mathit{\beta }(v)\}.$$ (6)

By directly maximizing ℓ_obs(β(v); h), we can obtain the maximum pseudo-likelihood estimate of β(v), denoted by β̂(v; h), which is given by

$$\widehat{\mathit{\beta }}(v;h)={\mathrm{\Sigma }}_{n,1}^{-1}(v;h)\sum _{v^{\prime }\in B(v,h)}\omega (v,v^{\prime };h)\sum _{i=1}^n{\mathbf{x}}_i{\widehat{\mathrm{\Sigma }}}_f^{-1}(v^{\prime })Y_i(v^{\prime }),$$ (7)

where ${\mathrm{\Sigma }}_{n,1}(v;h)={\sum }_{v^{\prime }\in B(v,h)}\omega (v,v^{\prime };h){\sum }_{i=1}^n{\mathbf{x}}_i{\widehat{\mathrm{\Sigma }}}_f^{-1}(v^{\prime }){\mathbf{x}}_i^T$. The covariance matrix of β̂(v; h) can be approximated by

$$\text{Cov}(\widehat{\mathit{\beta }}(v;h))\approx {\mathrm{\Sigma }}_n(\widehat{\mathit{\beta }}(v;h))={\mathrm{\Sigma }}_{n,1}^{-1}(v;h){\mathrm{\Sigma }}_{n,2}(v;h){\mathrm{\Sigma }}_{n,1}^{-1}(v;h),$$ (8)

where ${\mathrm{\Sigma }}_{n,2}(v;h)={\sum }_{i=1}^n{[{\sum }_{v^{\prime }\in B(v,h)}\omega (v,v^{\prime };h){\mathbf{x}}_i{\widehat{\mathrm{\Sigma }}}_f^{-1}(v^{\prime })\{Y_i(v)-{\mathbf{x}}_i^T\widehat{\mathit{\beta }}(v;h)\}]}^{\otimes 2}$. Although [39] have obtained the same β̂(v; h) as in expression (7), the covariance estimate of β̂(v; h) in expression (8) has a simple form compared to the corresponding one in [39] with an additional spatial correlation assumption. We have found that such spatial correlation assumption is unnecessary since Σ_n,2(v; h) has implicitly incorporated the spatial correlation in the data.

Based on β̂(v; h), we can further construct test statistics to examine scientific questions about β(v). For instance, such questions may compare brain structure across different groups (MZ versus DZ) or detect change in brain structure across time [3, 4, 5, 6, 7, 8]. These questions can be formulated as the linear hypotheses about β(v)

$$H_{0,\mu }:R_1\mathit{\beta }(v)=b_0\text{vs}.H_{1,\mu }:R_1\mathit{\beta }(v)\ne b_0,$$ (9)

where μ = R₁β(v), R₁ is a r × k matrix of full row rank and b₀ is a r × 1 specified vector. We test the null hypothesis H_0,μ : R₁β(v) = b₀ using the Wald test statistic

$$W_{\mu }(v;h)={\{R_1\widehat{\mathit{\beta }}(v;h)-{\mathbf{b}}_0\}}^T{\{R_1{\mathrm{\Sigma }}_n(\widehat{\mathit{\beta }}(v;h))R_1^T\}}^{-1}\{R_1\widehat{\mathit{\beta }}(v;h)-{\mathbf{b}}_0\}.$$ (10)

Under H_0,μ, W_μ(v; h) is asymptotically distributed as χ²(r) [43].

2.2.2 Propagation-Seperation procedure

Following the propagation-seperation (PS) procedure proposed in [35, 53, 36], [39, 40, 41] and [43], we adaptively determine {ω(v, v′; h) : v, v′ ∈ 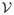} and then calculate β̂(v; h) and W_μ(v; h) as h increases from 0 to a preset value r₀. Since PS and the choice of its associated parameters have been described in details in [35, 53, 36] and [43], we briefly disscuss them here for the sake of simplicity.

The key idea of PS is to build a sequence of nested spheres with increasing radii h₀ = 0 < h₁ < ··· < h_S = r₀ at each voxel v ∈ 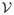. When h = h₁, we extract features from the imaging data as well as {β̂(v) : v ∈ 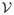} and compute weights ω(v, v′; h₁) at scale h₁ for all v, v′ ∈ 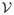. Then, we adaptively determine ω(v, v′; h_s) and update β̂(v; h_s) from h₁ to h_S = r₀. A path diagram of the multiscale strategy is given below:

$$\begin{array}{ccccccc}\{\widehat{\mathit{\beta }}(v):v\in \mathcal{V}\}& \Rightarrow & \omega (v,v^{\prime };h_1)& & \cdots & & \omega (v,v^{\prime };h_S=r_0)\\ & & \Downarrow & \nearrow & \cdots & \nearrow & \Downarrow \\ & & \{\widehat{\mathit{\beta }}(v;h_1):v\in \mathcal{V}\}& & \cdots & & \{(\widehat{\mathit{\beta }}(v;h_S),W_{\mu }(v;h_S)):v\in \mathcal{V}\}.\end{array}$$

The four key steps of PS including weights adaptation, estimation, stop checking, and inference are presented as follows.

• In the weights adaptation step (i), we prefix a series{ $h_s=c_h^s:s=1,\cdots ,S$} of radii with c_h ∈ (1, 2), say c_h = 1.15. We then set s = 1 and h₁ = c_h. The adaptive weights are given by

  $$\omega (v,v^{\prime };h_s)=K_{\mathit{loc}}({\left|\right|v-v^{\prime }\left|\right|}_2/h_s)K_{st}(D_{\beta }(v,v^{\prime };h_{s-1})/C_n),$$ (11)
  where K_loc(u) = (1−u)₊ and K_st(u) = min(1, 2(1−u²))₊ according to our experience and previous literature [39, 43], and || · ||₂ denotes the Euclidean norm of a vector. Moreover, D_β(v, v′; h_s−1) is set as

  $$D_{\beta }(v,v^{\prime };h_{s-1})={\{\widehat{\mathit{\beta }}(v;h_{s-1})-\widehat{\mathit{\beta }}(v^{\prime };h_{s-1})\}}^T{\mathrm{\Sigma }}_n^{-1}(\widehat{\mathit{\beta }}(v;h_{s-1}))\{\widehat{\mathit{\beta }}(v;h_{s-1})-\widehat{\mathit{\beta }}(v^{\prime };h_{s-1})\}.$$ (12)

  Following Li et al (2010), we choose C_n = n^1/3χ²(k)^0.95 for D_β(v, v′; h_s−1) defined in (12), where χ²(k)^0.95 is the upper 0.05-percentile of the χ²(k) distribution. The adaptive weight K_st(D_β(v, v′; h_s−1)/C_n) downweights the role of a voxel v′ ∈ B(v; h_s) in ℓ_obs(β(v); h_s) if the value of D_β(v, v′; h_s−1) is large. The weight K_loc(||v − v′||₂/h_s) gives less weight to a voxel v′ ∈ B(v; h_s) whose location is far from the voxel v. Since the theoretical justification for choosing various parameters in ω(v, v′; h_s) has been discussed in [35, 53, 36] and [43], we omit them here for the sake of simplicity.

• In the estimation step (ii), for the radius h_s, we calculate β̂(v; h_s) given in (7) at each voxel v ∈ .

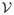• In the stop checking step (iii), after the S₀–th iteration, we calculate a stopping criterion based on a normalized distance between β̂(v; h_S0) and β̂(v; h_s) given by

  $$D(\widehat{\mathit{\beta }}(v;h_{S_0}),\widehat{\mathit{\beta }}(v;h_s))={\{\widehat{\mathit{\beta }}(v;h_{S_0})-\widehat{\mathit{\beta }}(v;h_s)\}}^T{\mathrm{\Sigma }}_n^{-1}(\widehat{\mathit{\beta }}(v;h_{S_0}))\{\widehat{\mathit{\beta }}(v;h_{S_0})-\widehat{\mathit{\beta }}(v;h_s)\}.$$ (13)

  Then, we compare D(β̂(v; h_S0), β̂(v; h_s)) with a benchmark, denoted by C̃(s), for s > S₀. If D(β̂(v; h_S0), β̂(v; h_s)) is greater than C̃(s), then we set β̂(v, h_S) = β̂(v; h_s−1), and s = S. If s = S, we go to the inference step (iv). If s ≤ S₀ or D(β̂(v; h_S0), β̂(v; h_s)) ≤ C̃(s) for S − 1 ≥ s > S₀, then we set h_s+1 = c_hh_s, increase s by 1 and continue with the weights adaptation step (i). Throughout the paper, we set S₀ = 3 and C̃(s) = χ²(p)^{0.8/(s−2)0.9}.

• In the inference step (iv), when s = S, we compute W_μ(v; h_S) for all v ∈ 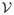and then apply either FDR or RFT correction to obtain the corrected p-values of W_μ(v; h_S) in order to detect significant voxels [19, 20, 21, 22]. Otherwise, we set h_s+1 = c_hh_s and continue with the weights adaptation step. The maximal step S can be taken to be relatively small, say 10, and thus the largest spherical neighborhood of each voxel only contains a relatively small number of voxels compared to the whole volume. Throughout the paper, we have used the false discovery rate method under the positive dependency in [17], since the test statistics obtained from MARM satisfy such dependency condition.

2.2.3 TwinMARM: Stage II

The second stage is to estimate $\mathit{\eta }(v)={({\sigma }_a^2(v),{\sigma }_c^2(v),{\sigma }_e^2(v))}^T$ and carry out statistical inference on η(v). Given {β̂(v; h_S) : v ∈ 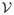} obtained from Stage I, we compute residuals ${\widehat{r}}_{ij}(v)=y_{ij}(v)-{\mathbf{x}}_{ij}^T\widehat{\mathit{\beta }}(v;h_S)$ for all i, j across all v ∈ 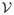. Then, we consider a trivariate regression model given by

$${\mathbf{r}}_i(v)=\left(\begin{array}{c}{\widehat{r}}_{i1}^2(v)\\ {\widehat{r}}_{i2}^2(v)\\ {\widehat{r}}_{i1}(v){\widehat{r}}_{i2}(v)\end{array}\right)={\mathbf{z}}_i^T\mathit{\eta }(v)+{\mathit{\epsilon }}_i(v)=\left(\begin{array}{c}{\mathbf{z}}_{i1}^T\\ {\mathbf{z}}_{i2}^T\\ {\mathbf{z}}_{i3}^T\end{array}\right)\mathit{\eta }(v)+\left(\begin{array}{c}{\epsilon }_{i1}(v)\\ {\epsilon }_{i2}(v)\\ {\epsilon }_{i3}(v)\end{array}\right),$$ (14)

where ε_i(v) = (ε_i1(v), ε_i2(v), ε_i3(v))^T and ${\mathbf{z}}_i=[\begin{array}{lll}{\mathbf{z}}_{i1}\hfill & {\mathbf{z}}_{i2}\hfill & {\mathbf{z}}_{i3}\hfill \end{array}]$, in which z_i1 = z_i2 = (1, 1, 1)^T and z_i3 equals (0.5, 1, 0)^T for DZ and (1, 1, 0)^T for MZ. We have given the detailed derivation of model (14) in the Appendix. Moreover, ε_i(v) is assumed to have mean zero and covariance Σ_ε(v) for all i. Although the homogeneous variance of ε_i(v) may not be realistic, we can appropriately account for such a misspecified assumption as we did for Σ_f (v) in Stage I. Since models (2) and (14) are similar in nature, most developments for model (2) can be directly applied to model (14) and then we omit them for the sake of simplicity.

There are several minor differences between models (2) and (14). In model (14), all regression coefficients in η(v) are constrained to be non-negative. Without loss of generality, Σ_ε(v) is assumed to be known since it can be replaced by a consistent estimate. The quasi-likelihood function for η(v) is given by

$${\ell }_{\mathit{obs}}(\mathit{\eta }(v);h_0)=-0.5\sum _{i=1}^n{\{{\mathbf{r}}_i(v)-{\mathbf{z}}_i^T\mathit{\eta }(v)\}}^T{\mathrm{\Sigma }}_{\epsilon }^{-1}(v)\{{\mathbf{r}}_i(v)-{\mathbf{z}}_i^T\mathit{\eta }(v)\}.$$ (15)

Let $\stackrel{\sim }{\mathit{\eta }}(v)={\{{\sum }_{i=1}^n{\mathbf{z}}_i{\mathrm{\Sigma }}_{\epsilon }^{-1}(v){\mathbf{z}}_i^T\}}^{-1}{\sum }_{i=1}^n{\mathbf{z}}_i{\mathrm{\Sigma }}_{\epsilon }^{-1}(v){\mathbf{r}}_i(v)$ be an unconstrained estimate of η(v) in model (15). By discarding these terms independent of η(v), we can show that ℓ_obs(η(v); h₀) can be simplified into

$$-0.5{\{\mathit{\eta }(v)-\stackrel{\sim }{\mathit{\eta }}(v)\}}^T\sum _{i=1}^n{\mathbf{z}}_i{\mathrm{\Sigma }}_{\epsilon }^{-1}(v){\mathbf{z}}_i^T\{\mathit{\eta }(v)-\stackrel{\sim }{\mathit{\eta }}(v)\}.$$

The constrained estimate of η(v), denoted by η̂(v), is given by

$$\widehat{\mathit{\eta }}(v)=\underset{\mathit{\eta }(v)\in {[0,\infty )}^3}{argmin}{\{\mathit{\eta }(v)-\stackrel{\sim }{\mathit{\eta }}(v)\}}^T\sum _{i=1}^n{\mathbf{z}}_i{\mathrm{\Sigma }}_{\epsilon }^{-1}(v){\mathbf{z}}_i^T\{\mathit{\eta }(v)-\stackrel{\sim }{\mathit{\eta }}(v)\}.$$ (16)

Since the set [0, ∞)³ = [0, ∞) × [0, ∞) × [0, ∞) is a convex cone, η̂(v) is unique [54]. To compute η̂(v), we employ a hinge algorithm for cone projection [54].

Furthermore, similar to (6), we can utilize weights ω_e(v, v′; h) to construct a weighted quasi-likelihood function as follows:

$${\ell }_{\mathit{obs}}(\mathit{\eta }(v);h)=-0.5\sum _{i=1}^n\sum _{v^{\prime }\in B(v,h)}{\omega }_e(v,v^{\prime };h){\{{\mathbf{r}}_i(v)-{\mathbf{z}}_i^T\mathit{\eta }(v)\}}^T{\mathrm{\Sigma }}_{\epsilon }^{-1}(v)\{{\mathbf{r}}_i(v)-{\mathbf{z}}_i^T\mathit{\eta }(v)\}.$$ (17)

Similarly, η̂(v; h) is given by

$$\underset{\mathit{\eta }(v)\in {[0,\infty )}^3}{argmin}{\{\mathit{\eta }(v)-\stackrel{\sim }{\mathit{\eta }}(v;h)\}}^T\sum _{v^{\prime }\in B(v,h)}{\omega }_e(v,v^{\prime };h)\sum _{i=1}^n{\mathbf{z}}_i{\mathrm{\Sigma }}_{\epsilon }^{-1}(v^{\prime }){\mathbf{z}}_i^T\{\mathit{\eta }(v)-\stackrel{\sim }{\mathit{\eta }}(v;h)\},$$ (18)

where η̃(v; h) equals

$${\left\{\sum _{v^{\prime }\in B(v,h)}{\omega }_e(v,v^{\prime };h)\sum _{i=1}^n{\mathbf{z}}_i{\mathrm{\Sigma }}_{\epsilon }^{-1}(v^{\prime }){\mathbf{z}}_i^T\right\}}^{-1}\sum _{v^{\prime }\in B(v,h)}{\omega }_e(v,v^{\prime };h)\sum _{i=1}^n{\mathbf{z}}_i{\mathrm{\Sigma }}_{\epsilon }^{-1}(v^{\prime }){\mathbf{r}}_i(v^{\prime }).$$ (19)

The same hinge algorithm [54] is used to calculate η̂(v; h).

The second focus common in twin study research is the testing of genetic and environmental influences on brain structures and their functions. See for example, [2], [55, 11], [5], [6], [7], and [8], among many others. Such questions of interest can be formulated as the linear hypotheses about η(v) as follows:

$$H_{0,A}:R_2\mathit{\eta }(v)=0\text{vs}.H_{1,A}:R_2\mathit{\eta }(v)>0,$$ (20)

where R₂ is an m × 3 matrix. For instance, in an ACE model, R₂ equals (1, 0, 0) for genetic effect and (0, 1, 0) for environmental effect. Similar to testing H_0,μ, we test H_0,A using the Wald test statistic

$$W_A(v;h)=R_2\widehat{\mathit{\eta }}{(v;h)}^T{\{R_2{\mathrm{\Sigma }}_n(\widehat{\mathit{\eta }}(v;h))R_2^T\}}^{-1}{R}_2\widehat{\mathit{\eta }}(v;h).$$ (21)

where Σ_n(η̂(v; h)) is the covariance matrix of η̂(v; h). The statistic W_A(v; h) is asymptotically distributed as a mixture of χ²(1) and χ²(0) distributions under the null hypothesis H_0,A, where χ²(0) = 0. However, to test the joint genetic and environmental effects, R₂ takes the form of [(1, 0, 0)^T(0, 1, 0)^T] and W_A(v; h) is asymptotically distributed as a mixture of χ²(2), χ²(1) and χ²(0) distributions with the weights depending on the ratio of MZ over DZ [51, 56].

3 Simulation Studies

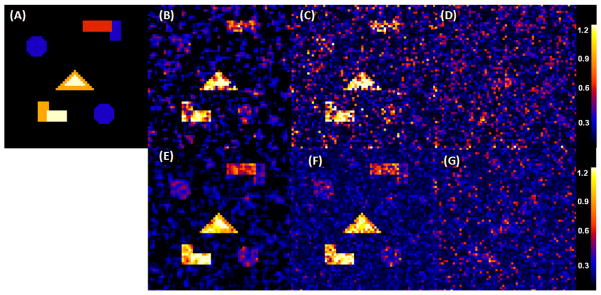
We carried out some simulation studies to examine the finite-sample performance of Twin-MARM. We first simulated MRI measures from n pairs of siblings according to the ACE model, in which β(v) = (β₁(v), β₂(v), β₃(v))^T and x_ij = (x_1ij, x_2ij, x_3ij)^T for j = 1, 2. Each family contains only two siblings. Among the n pairs of twins, 60% are identical twins. We set x_1ij ≡ 1, generated x_2ij independently from a Bernoulli distribution with probability of success 0.5 and generated x_3ij independently from the Gaussian distribution with zero mean and unit variance. The x_2ij and x_3ij were chosen to represent gender identity and scaled age, respectively. We set ${({\beta }_2(v),{\beta }_3(v),{\sigma }_c^2(v),{\sigma }_e^2(v))}^T={(1,1,1,1)}^T$ across all voxels v. For ( ${\beta }_1(v),{\sigma }_a^2(v)$), we divided the 64×64 phantom image into five different regions of interest (ROIs) with different shapes and then varied ( ${\beta }_1(v),{\sigma }_a^2(v)$) as (0, 0), (0.3, 0.5), (0.6, 1), (0.9, 1.5) and (1.2, 2.0) across these five ROIs. The true ( ${\beta }_1(v),{\sigma }_a^2(v)$) was displayed for all ROIs with black, blue, red, yellow, and white colors representing ( ${\beta }_1(v),{\sigma }_a^2(v)=(0,0),(0.3,0.5),(0.6,1),(0.9,1.5)$and (1.2, 2.0) (Fig. 3(A)). We independently generated e_i(v) = (e_i1(v), e_i2(v))^T, a_i(v) = (a_i1(v), a_i2(v))^T, and c_i(v) from multivariate Gaussian distributions with zero means and covariance matrices as specified in Fig. 1. We set n = 100 and 400.

Fig. 3.

Results from a simulation study of comparing EM and TwinMARM at 2 different sample sizes (n = 100, 400). The first row contains the results for ${\sigma }_a^2(v)$ as n = 100: Panel (A) is the ground truth image of ${\sigma }_a^2(v)$, in which five ROIs with black, blue, red, yellow, and white color represent ${\sigma }_a^2(v)=0,0.3,0.6,0.9\text{and}1.2$ , respectively. Panel (B) is a selected slice of ${\widehat{\sigma }}_a^2(v;h_{10})$ obtained from a simulated dataset by using the TwinMARM method. Panel (C) is a selected slice of ${\widehat{\sigma }}_a^2(v)$ obtained from the same dataset as panel (B) by using the voxel-wise EM method. Panel (D) is a selected slice of ${\widehat{\sigma }}_a^2(v)$ by using EM, after smoothing the same simulated data set as panel (B). The second row contains panels (E), (F) and (G) as n = 400, which are the corresponding results of panels of panels (B), (C) and (D), respectively.

To carry out the analysis, we first fit the structural equation model $y_{ij}(v)={\mathbf{x}}_{ij}^T\mathit{\beta }(v)+a_{ij}(v)+c_i(v)+e_{ij}(v)$ , in which the correlation pattern of a_ij(v), c_i(v) and e_ij(v) was specified according to Fig. 1. We calculated the maximum likelihood estimates (MLEs) of ${(\mathit{\beta }(v),{\sigma }_a^2(v),{\sigma }_e^2(v),{\sigma }_c^2(v))}^T$ at each pixel by using the expectation-maximization (EM) algorithm [57]. Then, we applied the TwinMARM procedure described in Section 2.2 to calculate adaptive parameter estimates across all pixels at 11 different scales. We also smoothed the subjects’ images by using an isotropic Gaussian kernel with FWHM 3 pixels and then applied the EM algorithm to the smoothed data. Furthermore, for (β₁(v), ${\sigma }_a^2(v)$), we calculated the bias, the empirical standard error RMS, the mean of the standard error estimates SD, and the ratio of RMS over SD, abbreviated as RE, at each pixel of all five ROIs based on the results obtained from the 1000 n = 100 and 400 simulated data sets.

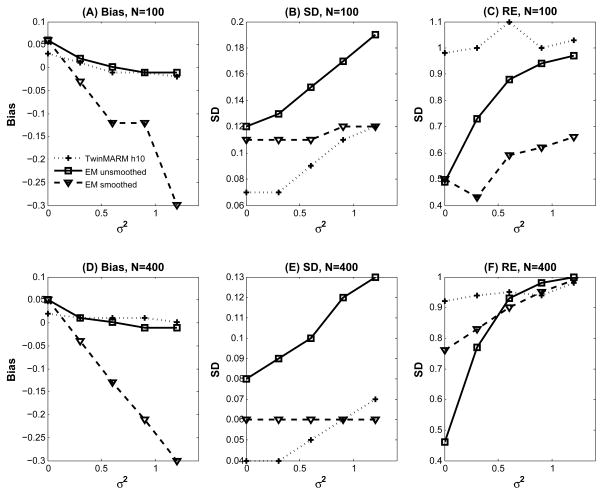
For simplicity, we present some selected results for β̂₁(v; h) and ${\widehat{\sigma }}_a^2(v;h)$ and their corresponding MLEs obtained from the EM algorithm with smoothed and unsmoothed data. We first considered ${\widehat{\sigma }}_a^2(v;h)$. The biases of σ_a(v; h)² are almost the same for TwinMARM at h₁₀ and EM with unsmoothed data (Fig. 3(B), (C), (E) and (F)), while the bias from EM with smoothed data is greatly increased (Fig. 5(A) and (C) and Fig. 3(D) and (G))). Inspecting the results from the EM algorithm reveals that SD is consistently larger than that obtained from TwinMARM at h₁₀ (Fig. 5(B) and (D)). Overall, for ${\widehat{\sigma }}_a^2(v;h)$, TwinMARM outperforms EM in terms of smaller RMS (Fig. 3(B), (C), (E) and (F)).

Fig. 5.

Results from a simulation study of comparing EM and TwinMARM at 2 different sample sizes (n = 100, 400). The first row contains the results for ${\sigma }_a^2(v)$ as n = 100: Panel (A) is the bias curve of ${\sigma }_a^2(v)=0,0.3,0.6,0.9\text{and}1.2$, respectively. Panel (B) is the SD curve of ${\widehat{\sigma }}_a^2(v;h_{10})$ obtained from a simulated dataset by using TwinMARM, EM, and EM with smoothed data. Panel (C) is the ratio of RMS over SD. The second row contains panels (D), (E), and (F) as n = 400, which are the corresponding results of panels of panels (A), (B), and (C) respectively.

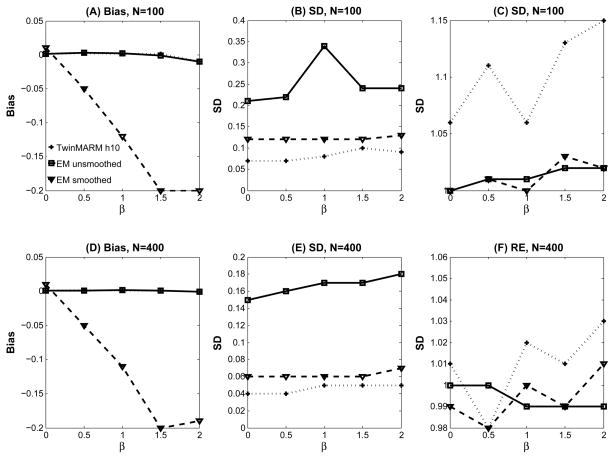
Secondly, we examine β̂₁(v; h). The biases of β̂₁(v; h) are almost the same for TwinMARM at h₁₀ and EM with unsmoothed data (Fig. 6(A) and (C) and Fig. 4(B), (C), (E) and (F)), while the bias from EM with smoothed data is greatly increased (Fig. 6(A) and (C) and Fig. 4(D) and (G)). Inspecting the results from the EM algorithm reveals that SD is consistently larger than that obtained from TwinMARM at h₁₀ (Fig. 6(B) and (D)). For β̂₁(v; h), TwinMARM outperforms EM in terms of smaller RMS (Fig. 4(B), (C), (E) and (F)).

Fig. 6.

Results from a simulation study of comparing EM and TwinMARM at 2 different sample sizes (n = 100, 400). The first row contains the results for β₁(v) as n = 100: Panel (A) is the bias curve of β₁(v)=0, 0.5, 1.0, 1.5, and 2.0, respectively. Panel (B) is the SD curve of β̂(v) obtained from a simulated dataset by using TwinMARM, EM, and EM with smoothed data. Panel (C) is the ratio of RMS over SD. The second row contains panels (D), (E), and (F) as n = 400, which are the corresponding results of panels of panels (A), (B), and (C) respectively.

Fig. 4.

Results from a simulation study of comparing EM and TwinMARM at 2 different sample sizes (n = 100, 400). The first row contains the results for β₁(v), when sample size n = 100: Panel (A) is the ground truth image of β₁(v), in which five ROIs with black, blue, red, yellow, and white color represent β₁(v)=0, 0.5, 1.0, 1.5, and 2.0, respectively. Panel (B) is a selected slice of β̂₁(v; h₁₀) obtained from a simulated dataset by using TwinMARM. Panel (C) is a selected slice of β̂₁(v) obtained from the same simulated dataset as panel (B) by using EM. Panel (D) is a selected slice of β̂₁(v) obtained by using EM, after smoothing the same simulated data set as panel (B). The second row contains panels (E), (F) and (G) as n = 400, which are the corresponding results of panels of panels (B), (C) and (D), respectively.

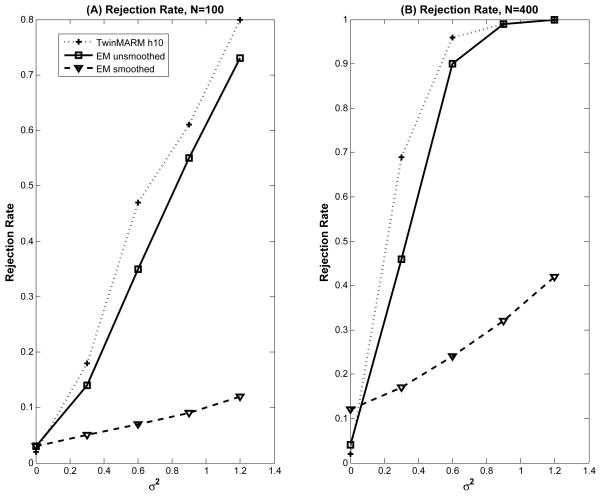
To assess both Type I and II error rates of W_A(v; h) at the pixel level, we tested the hypotheses $H_0:{\sigma }_a^2(v)=0$ and $H_1:{\sigma }_a^2(v)>0$ across all pixels. We applied the same PS procedure and computed the p-values of W_A(v; h) at each scale. The 1,000 replications were used to calculate the estimates and standard errors of rejection rates with significance level α = 5%. For the test statistic W_A(v; h), the Type I rejection rates in ROI with ${\sigma }_a^2(v)=0$ were relatively small for all scales, while the statistical power for rejecting the null hypothesis in ROIs with ${\sigma }_a^2(v)>0$ significantly increased with larger radius h (Fig. 7). For all ROIs with ${\sigma }_a^2(v)>0$, W_A(v; h₁₀) outperforms the likelihood ratio test statistic (LRT) based on the EM algorithm without smoothing and EM algorithm with smoothing in terms of power (Fig. 7).

Fig. 7.

Simulation results for W_A(v; h): rejection rates for pixels inside the five ROIs were reported by using TwinMARM at the h₁₀ scale, EM, EM after smoothing the same simulated data and 2 different sample sizes (n = 100, 400) at α = 5%. For each case, 1,000 simulated datasets were used.

Finally, we note that there are at least three limitations associated with our simulation studies. First, it should be noted that the simulated phantom image is 2D, whereas most real neuroimaging data is 3D. TwinMARM should work better in 3D and the variance reduction should be larger, since more neighboring voxels are available at each voxel for calculating adaptive weights and parameter estimation. Secondly, we did not directly simulate ‘real’ functional (or structural) imaging data from twin studies, since it is not straightforward to simulate real imaging data according to model (1). Thirdly, we did not evaluate the reconstruction and registration errors in reconstructing and registering real imaging data from twin studies.

4 Real-World Example

We considered the early postnatal brain development project led by Dr. Gilmore at the University of North Carolina at Chapel Hill [9]. This study was approved by the Institutional Review Board. A total of 49 paired twins (36 males and 62 females) were selected. All 49 pairs were scanned as neonates within a few weeks after birth at term. Written consent was obtained from their parents before imaging acquisition. The mean gestational age at MR scanning was 246 ± 18.3 days (range: 192 to 270 days). All infants were fed and calmed to sleep on a warm blanket with proper ear protection and they slept comfortably inside the MR scanner. None of infants was sedated during the imaging session.

We used a 3T Allegra head-only MR system (Siemens Medical Inc., Erlangen, Germany) to acquire all the images. The system was equipped with a maximal gradient strength of 40 mT/m and a maximal slew rate of 400 mT/(m·msec). We used a single shot EPI DTI sequence (TR/TE=5400/73 msec) with eddy current compensation to acquire the DTI images. The acquisition sequence consists of five repetitions of six gradient scans (b = 1000 s/mm²) at 6 non-collinear directions and a single reference scan (in total 5×7 = 35 images). The voxel resolution was isotropic 2 mm, and the in-plane field of view was set at 256 mm in both directions.

We then employed a nonlinear fluid deformation based high-dimensional, unbiased atlas computation method to process all 98 DTI datasets [58]. The atlas building procedure started with an affine registration and was followed by a nonlinear registration of a set of feature images for all subjects. The feature images are the maximum eigenvalue of the Hessian of the fractional anisotropy (FA) image, which are sensitive to the geometry of white matter. Using the computed deformation fields, we warped all tensor images into the unbiased atlas space via log-euclidean based interpolation [59]. We also averaged all the warped tensor images to create a study specific DTI atlas.

FA has been widely used as a measurement to assess directional organization of the brain which is greatly influenced by the magnitude and orientation of white matter tracts. Here, FA images are employed to identify the spatial patterns of white matter maturation. We considered a linear model y_ij(v) = β₁(v) + β₂(v)G_ij + β₃(v)Z_ij + a_ij(v) + c_i(v) + ε_ij(v) for i = 1, ···, 49 and j = 1, 2 at each voxel of the template, where G_ij and Z_ij, respectively, represent the dummy variables for gender (male=1 and female=0) and zygote (MZ=1 and DZ=0), and a_ij(v), c_i(v) and e_ij(v) are, respectively, the additive genetic, common environmental, and residual effects on the i-th twin pair as specified in Fig. 1. We focused on the major white matter regions. We calculated the MLE of parameters by using the EM algorithm and then applied our TwinMARM method with c_h = 1.15 and S = 10 to carry out statistical analysis.

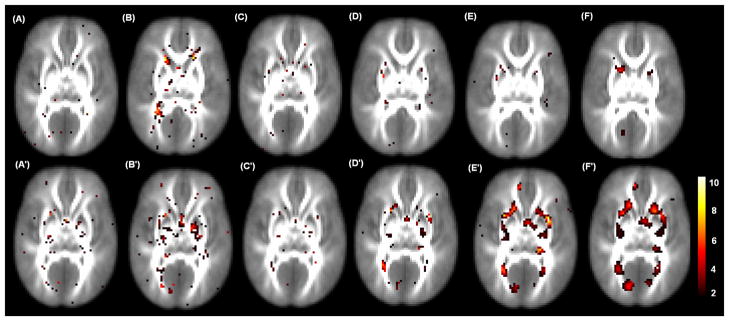
We tested $H:{\sigma }_a^2(v)=0$ for additive genetic effect across all voxels v in the white matter regions. To correct for multiple comparisons, we used the raw p-value smaller than 0.05 along with a 20 voxel extent threshold. We found significant regions in the inferior frontal gyrus, triangular part and mid cingulate cortex regions. We identified more voxels by using TwinMARM compared to EM (Table 1). We also tested $H_0:{\sigma }_c^2(v)=0$ for common environmental effect across all voxels v. Several interesting regions identified included the right precentral gyrus, inferior frontal gyrus, triangular part, supplementary motor area, insula, hippocampus, right fusiform, and thalamus. Fig. 8 shows some selected slices of – log₁₀(p) map for environmental effect obtained from the 10th iteration of TwinMARM. The results show that TwinMARM may have significantly improved sensitivity and reliability as areas of significance in the TwinMARM results appear larger and smoother compared to the voxel-wise analysis approach, which is close to the result obtained from the first iteration of TwinMARM. The FA measure shows strong effects of genetic factors and common environment in the frontal lobes and in the limbic lobes. The detection of a genetic effect is partially consistent with many other studies that have detected strong genetic influences on brain morphology [11, 4, 60, 55].

Table 1.

Real data analysis results. # of voxels whose p–value is less than a specific threshold for testing the genetic and environmental effect for EM method without smoothing, smoothing with Gaussian kernels with FWHM equal to 3mm, 6mm, and 9mm and TwinMARM method at the 1^st and 10^th iteration.

		EM smoothness (mm)				TwinMARM (round)
	Effect	0	3	6	9	1st	10th
p–value< 0.01	Genetic	13	26	19	32	19	47
	Environment	11	41	140	152	23	47
p–value< 0.05	Genetic	148	233	208	254	198	433
	Environment	171	567	1318	1984	232	715
p–value< 0.10	Genetic	548	865	812	719	676	1430
	Environment	615	1708	3769	5804	956	2568

Fig. 8.

Results from the 49 twin pairs in a neonatal project on brain development on the selected 27th and 30th slices. Panels (A)–(F) : the – log₁₀(p) values for testing genetic effects by using TwinMARM at the 1^st and 10^th iterations and EM with FWHM equal to 0mm, 3mm, 6mm, 9mm for the 27th slice; Panels (A′)–(F′) : the corresponding – log₁₀(p) values for testing environmental effects for the 30th slice.

We also observed the smoother and larger significant clusters of genetic factors and common environment by using the EM algorithm with smoothed data from FWHM=6mm and 9mm (Fig. 8(F), (E′) and (F′)). First, based on our simulation studies, we observed that the EM algorithm for unsmoothed data and TwinMARM do not introduce bias in the estimates of ${\sigma }_a^2(v)$, whereas we observed the substantial bias in the estimates of ${\sigma }_a^2(v)$ for the heavily smoothing imaging data (Figs. 3 and 5). Secondly, these smoother and larger significant clusters do not appear in the results obtained from the unsmoothed data. Thus, we feel that these smoother and larger significant clusters obtained from the heavily smoothed data may be false positive results (Fig. 8 and Table 1 and 2). However, a word of caution is needed in interpreting these significant clusters to be false positive, since two key assumptions underlying EM and TwinMARM, including the perfect registration assumption and the structural equation model (1), may be invalid for this real data set.

Table 2.

Real data analysis results. # of cluster which has over 20 contiguous voxels with p–value less than a specific threshold for testing the genetic and environmental effect by using EM method without smoothing, smoothing with Gaussian kernels (FWHM=3mm, 6mm and 9mm) and TwinMARM method at the 1^st and 10^th iteration.

		EM smoothness (mm)				TwinMARM (round)
	Effect	0	3	6	9	1st	10th
p–value< 0.01	Genetic	0	0	0	1	0	0
	Environment	0	0	1	2	0	0
p–value< 0.05	Genetic	0	0	3	3	0	3
	Environment	0	4	17	11	0	4
p–value< 0.10	Genetic	0	10	9	8	1	9
	Environment	4	21	18	10	3	20

5 Conclusions and Discussion

We have developed TwinMARM for the statistical analysis of twin neuroimaging data. TwinMARM consists of two stages of multiscale adaptive regression methods. TwinMARM have three features: being spatial, being hierarchical, and being adaptive. The TwinMARM procedure is a simultaneous smoothing and estimation procedure. Each stage of TwinMARM constructs hierarchical nested spheres with increasing radii at all voxels to adaptively compute weighted quasi-likelihood functions and efficiently utilizes available information to obtain parameter estimates. This leads to improved accuracy of parameter estimates and increased statistical power in detecting subtle changes of brain structure and function.

As shown in the simulation studies, the commonly used Gaussian kernel for smoothing imaging data can introduce two levels of biases for the analysis of twin imaging data, which can dramatically increase the numbers of false positives and negatives. The first level of biases originates from the mean structure, which is associated with the regression coefficients β(v). Most smoothing methods, which are independent of imaging data, usually blur the image data near the edges of the significant regions, and consequently introduce biases in β(v). The second level of biases comes from the variance structure, which is associated with the genetic coefficients σ²(v). Most smoothing methods are not only conducted independently of imaging data but also of the statistical model fitted to the imaging data. Statistically, standard smoothing methods can change the variance structure in the imaging data which are the focus of twin imaging studies. Thus, the second level of biases is much more severe than the first level of biases. In practice, we should avoid directly smoothing twin imaging data.

Several limitations need to be addressed in future research. The TwinMARM procedure is based on the two key assumptions, including the perfect registration assumption and the structural equation model (1). A first limitation of our study is that the perfect registration assumption is demonstrably false for real imaging data from twin studies. It is important and interesting to integrate the registration method, smoothing method, and TwinMARM into a single framework in order to appropriately account for registration errors in the statistical analysis of imaging data from twin studies. A second limitation of our study is that the structural equation model (1) can be invalid for real imaging data from twin studies. Heritability estimates used for most twin studies rest on restrictive assumptions in model (1), which are usually not tested, and if they are, can often found to be violated by the real data [61].

There are several current topics for our research. We are developing a Graphical User Interface (GUI) to pack our code for TwinMARM, which will be freely downloadable from our website at http://www.bios.unc.edu/research/bias. The development of multiscale-adaptive methods to determine multiscale neighborhoods that adapt to the pattern of imaging data at each voxel would undoubtedly be a useful resource for neuroimaging researchers. Further, we will extend TwinMARM from the univariate to multivariate and complex imaging measures, such as deformation tensors. We will develop a multiscale adaptive model for neuroimaging data from familial studies [25]. More research is needed for optimizing the choices of the parameters in TwinMARM. It is interesting to incorporate other edge-preserving local smoothing methods into TwinMARM and MARM [33, 34, 37, 38].

6 Appendix: Effect of smoothing twin imaging data

We examined the effect of smoothing twin imaging data on its associated statistical analysis as follows. As an illustration, we focus on an arbitrary voxel v and its spherical neighborhood, denoted by {v′ : v′ ∈ B(v, h)}. Standard smoothing methods primarily take a weighted average of all observations {y_ij(v′) : v′ ∈ B(v, h)}, denoted by ỹ_ij(v), such that ỹ_ij(v) = ∑_{v′ ∈ B(v,h)} ω(v, v ′; h)y_ij(v′), where ∑_{v′ ∈ B(v,h)} ω(v, v′; h) = 1 and ω(v, v; h) > 0. Under model (1), we can show that

$$\begin{array}{l}{\stackrel{\sim }{y}}_{ij}(v)=\sum _{v^{\prime }\in B(v,h)}\omega (v.v^{\prime };h)\{x_{ij}^T\mathit{\beta }(v^{\prime })+a_{ij}(v^{\prime })+d_{ij}(v^{\prime })+c_i(v^{\prime })+e_{ij}(v^{\prime })\}\\ =x_{ij}^T\stackrel{\sim }{\mathit{\beta }}(v)+{\stackrel{\sim }{a}}_{ij}(v)+{\stackrel{\sim }{d}}_{ij}(v)+{\stackrel{\sim }{c}}_i(v)+{\stackrel{\sim }{e}}_{ij}(v),\end{array}$$ (22)

where β̃(v) = ∑_{v′∈B(v,h)} ω(v, v′; h)β(v′),

$$\begin{array}{r}{\stackrel{\sim }{a}}_{ij}(v)=\sum _{v^{\prime }\in B(v,h)}\omega (v,v^{\prime };h)a_{ij}(v^{\prime }),{\stackrel{\sim }{d}}_{ij}(v)=\sum _{v^{\prime }\in B(v,h)}\omega (v,v^{\prime };h)d_{ij}(v^{\prime }),\\ {\stackrel{\sim }{c}}_{ij}(v)=\sum _{v^{\prime }\in B(v,h)}\omega (v,v^{\prime };h)c_{ij}(v^{\prime }),{\stackrel{\sim }{e}}_{ij}(v)=\sum _{v^{\prime }\in B(v,h)}\omega (v,v^{\prime };h)e_{ij}(v^{\prime }).\end{array}$$

It can be shown that the variance of ã_ij(v), denoted by ${\stackrel{\sim }{\sigma }}_a^2(v)$, depends on both the variances of {a_ij(v′) : v′ ∈ B(v, h)} and their spatial correlations. Specifically, we have

$${\stackrel{\sim }{\sigma }}_a^2(v)=\sum _{v^{\prime }\in B(v,h)}\omega {(v,v^{\prime };h)}^2{\sigma }_a^2(v^{\prime })+2\sum _{v^{\prime }\ne v^{″}\in B(v,h)}\omega (v,v^{\prime };h)\omega (v,v^{″};h)\text{Cov}(a_{ij}(v^{\prime }),a_{ij}(v^{″})).$$

Similar arguments hold for the variances of d̃_ij(v), c̃_ij(v) and ẽ_ij(v) denoted by ${\stackrel{\sim }{\sigma }}_d^2(v),{\stackrel{\sim }{\sigma }}_c^2(v)$, and ${\stackrel{\sim }{\sigma }}_e^2(v)$, respectively. Due to the presence of spatial correlations and other factors (e.g., the inhomogeneity of ${\stackrel{\sim }{\sigma }}_d^2(v^{\prime })$) across v′ ∈ B(v, h)), it is common that

$$g(v)=\frac{{\sigma }_a^2(v)+{\sigma }_d^2(v)}{{\sigma }_a^2(v)+{\sigma }_d^2(v)+{\sigma }_e^2(v)+{\sigma }_c^2(v)}\ne \stackrel{\sim }{g}(v)=\frac{{\stackrel{\sim }{\sigma }}_a^2(v)+{\stackrel{\sim }{\sigma }}_d^2(v)}{{\stackrel{\sim }{\sigma }}_a^2(v)+{\stackrel{\sim }{\sigma }}_d^2(v)+{\stackrel{\sim }{\sigma }}_e^2(v)+{\stackrel{\sim }{\sigma }}_c^2(v)}.$$

Generally, the Gaussian kernel smoothing method can easily modify the variance structure of twin imaging data. Because such variance structures are often the focus of twin studies, we thus suggest avoiding directly smoothing twin imaging data in practice.

We show that TwinMARM does not introduce bias in the variance structure of twin imaging data. This consists of two steps.

• Step (i) As n → ∞, β̂(v; h_S) converges β_*(v) in probability and $\sqrt{n}\{\widehat{\mathit{\beta }}(v;h_S)-{\mathit{\beta }}_{\ast }(v)\}$ is asymptotically normal distributed for all v ∈ 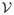under the mild conditions given in [43], where β_*(v) is the true value β(v) in voxel v. Please see Theorems 1–3 in [43] for the details.

• Step (ii) As n → ∞, η̃(v; h_S) converges η_*(v) and $\sqrt{n}\{\widehat{\mathit{\eta }}(v;h_S)-{\mathit{\eta }}_{\ast }(v)\}$ converges to a random variable in distribution for all v ∈ 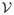. We can essentially use the same idea in proving Step (i) to prove Step (ii), but there is a complexity in dealing with substituting β_*(v) by β̂(v;h_S). We will show that such substitution is negligible below.

We just highlight the key idea underlying the proof of Step (ii). It follows from Step (i) and the ACE model that for j = 1, 2,

$$\begin{array}{l}{\widehat{r}}_{ij}(v)=y_{ij}(v)-{\mathbf{x}}_{ij}^T\widehat{\mathit{\beta }}(v;h_S)=y_{ij}(v)-{\mathbf{x}}_{ij}^T{\mathit{\beta }}_{\ast }(v)+{\mathbf{x}}_{ij}^T\{\widehat{\mathit{\beta }}(v;h_S)-{\mathit{\beta }}_{\ast }(v)\}\\ =n^{-1/2}{\mathbf{x}}_{ij}^T\sqrt{n}\{\widehat{\mathit{\beta }}(v;h_S)-{\mathit{\beta }}_{\ast }(v)\}+f_{ij}(v).\end{array}$$ (23)

Let Δβ(v; h_S) = {β̂(v; h_S) – β_*(v)}. With some simple algebra, for j = 1, 2, we can show that

$$\begin{array}{l}{\widehat{r}}_{ij}^2(v)=f_{ij}^2(v)+n^{-1}{O}_p(1)+2n^{-1/2}{\mathbf{x}}_{ij}^T\sqrt{n}\mathrm{\Delta }\mathit{\beta }(v;h_S)f_{ij}(v)\\ ={\mathbf{z}}_{ij}^T{\mathit{\eta }}_{\ast }(v)+{\epsilon }_{ij}(v),\end{array}$$

in which we have used the results in Step (i) and $O_p(1)={\{{\mathbf{x}}_{ij}^T\sqrt{n}\mathrm{\Delta }\widehat{\mathit{\beta }}(v;h_S)\}}^2$ (van der Vaart, 1998) and set

$${\epsilon }_{ij}(v)=f_{ij}^2(v)-{\mathbf{z}}_{ij}^T{\mathit{\eta }}_{\ast }(v)+n^{-1}{O}_p(1)+2n^{-1/2}{\mathbf{x}}_{ij}^T\sqrt{n}\mathrm{\Delta }\mathit{\beta }(v;h_S)f_{ij}(v).$$ (24)

Similarly, we can show that

$$\begin{array}{l}{\widehat{r}}_{i1}(v){\widehat{r}}_{i2}(v)={\mathbf{z}}_{i3}^T{\mathit{\eta }}_{\ast }(v)+{\epsilon }_{i3}(v),\\ {\epsilon }_{i3}(v)=f_{i1}(v)f_{i2}(v)-{\mathbf{z}}_{i3}^T{\mathit{\eta }}_{\ast }(v)+n^{-1}{O}_p(1)+n^{-1/2}{\mathbf{x}}_{i2}^T\sqrt{n}\mathrm{\Delta }\mathit{\beta }(v;h_S)f_{i1}(v)+n^{-1/2}{\mathbf{x}}_{i1}^T\sqrt{n}\mathrm{\Delta }\mathit{\beta }(v;h_S)f_{i2}(v),\end{array}$$ (25)

where $O_p(1)=\{{\mathbf{x}}_{i1}^T\sqrt{n}\mathrm{\Delta }\widehat{\mathit{\beta }}(v;h_S)\}\{{\mathbf{x}}_{i2}^T\sqrt{n}\mathrm{\Delta }\widehat{\mathit{\beta }}(v;h_S)\}$. Based on these results, we can obtain model (14), in which ε_i(v) is almost unbiased except an O_p(n^−1/2) term. We will show that such O_p(n^−1/2) term has a negligible effect below.

Then, we need to show that η̂(v; h) converges η_*(v) in probability and $\sqrt{n}\{\widehat{\mathit{\eta }}(v;h)-{\mathit{\eta }}_{\ast }(v)\}$ asymptotically converges a random variable in distribution for all v ∈ 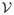under some mild conditions, which are similar to those give in [43]. We focus on h = h₀ = 0. For h > 0, we can generalize the proofs given in [43]. Recall that $\stackrel{\sim }{\mathit{\eta }}(v)={\{{\sum }_{i=1}^n{\mathbf{z}}_i{\mathrm{\Sigma }}_{\epsilon }^{-1}(v){\mathbf{z}}_i^T\}}^{-1}{\sum }_{i=1}^n{\mathbf{z}}_i{\mathrm{\Sigma }}_{\epsilon }^{-1}(v){\mathbf{r}}_i(v)$. We define

$$\begin{array}{l}{\stackrel{\sim }{\mathit{\epsilon }}}_i(v)={(f_{i1}^2(v)-{\mathbf{z}}_{i1}^T{\mathit{\eta }}_{\ast }(v),f_{i2}^2(v)-{\mathbf{z}}_{i2}^T{\mathit{\eta }}_{\ast }(v),f_{i1}(v)f_{i2}(v)-{\mathbf{z}}_{i3}^T{\mathit{\eta }}_{\ast }(v))}^T,\\ {\mathbf{g}}_i(v)={(2{\mathbf{x}}_{i1}^T{f}_{i1}(v),2{\mathbf{x}}_{i2}^T{f}_{i2}(v),{\mathbf{x}}_{i1}^T{f}_{i2}(v)+{\mathbf{x}}_{i2}^T{f}_{i1}(v))}^T.\end{array}$$ (26)

By using the law of large number [62], we have

$$\frac{1}{\sqrt{n}}\sum _{i=1}^n{\mathbf{z}}_i{\mathrm{\Sigma }}_{\epsilon }^{-1}(v)n^{-1}{O}_p(1)=n^{-1/2}{O}_p(1)\text{and}\sqrt{n}\mathrm{\Delta }\mathit{\beta }(v;h_S)n^{-1}\sum _{i=1}^n{\mathbf{z}}_i{\mathrm{\Sigma }}_{\epsilon }^{-1}(v){\mathbf{g}}_i(v)=o_p(1)$$

in which we have used $\sqrt{n}\mathrm{\Delta }\mathit{\beta }(v;h_S)=O_p(1)$ obtained from Step (i) and $n^{-1}{\sum }_{i=1}^n{\mathbf{z}}_i{\mathrm{\Sigma }}_{\epsilon }^{-1}(v){\mathbf{g}}_i(v)$ converges to zero in probability. Thus, it follows from (14) that

$$\begin{array}{l}\sqrt{n}[\stackrel{\sim }{\mathit{\eta }}(v)-{\mathit{\eta }}_{\ast }(v)]={\left\{n^{-1}\sum _{i=1}^n{\mathbf{z}}_i{\mathrm{\Sigma }}_{\epsilon }^{-1}(v){\mathbf{z}}_i^T\right\}}^{-1}\frac{1}{\sqrt{n}}\sum _{i=1}^n{\mathbf{z}}_i{\mathrm{\Sigma }}_{\epsilon }^{-1}(v){\mathit{\epsilon }}_i(v)\\ ={\left\{n^{-1}\sum _{i=1}^n{\mathbf{z}}_i{\mathrm{\Sigma }}_{\epsilon }^{-1}(v){\mathbf{z}}_i^T\right\}}^{-1}\frac{1}{\sqrt{n}}\sum _{i=1}^n{\mathbf{z}}_i{\mathrm{\Sigma }}_{\epsilon }^{-1}(v)\{{\stackrel{\sim }{\mathit{\epsilon }}}_i(v)+n^{-1}{O}_p(1)+n^{-1/2}{\mathbf{g}}_i(v)\sqrt{n}\mathrm{\Delta }\mathit{\beta }(v;h_S)\}\\ ={\left\{n^{-1}\sum _{i=1}^n{\mathbf{z}}_i{\mathrm{\Sigma }}_{\epsilon }^{-1}(v){\mathbf{z}}_i^T\right\}}^{-1}\frac{1}{\sqrt{n}}\sum _{i=1}^n{\mathbf{z}}_i{\mathrm{\Sigma }}_{\epsilon }^{-1}(v){\stackrel{\sim }{\mathit{\epsilon }}}_i(v)+o_p(1),\end{array}$$

which yields that it is negligible to substitute β_*(v) by β̂(v; h_S). Furthermore, we calculate

$${\omega }_e(v,v^{\prime };h)=K_{\mathit{loc}}({\left|\right|v-v^{\prime }\left|\right|}_2/h)K_{st}(D_{\eta }(v,v^{\prime };h)/C_n),$$

where $D_{\eta }(v,v^{\prime };h)={\{\widehat{\mathit{\eta }}(v;h)-\widehat{\mathit{\eta }}(v^{\prime };h)\}}^T{\mathrm{\Sigma }}_n^{-1}(\widehat{\mathit{\beta }}(v;h))\{\widehat{\mathit{\eta }}(v;h)-\widehat{\mathit{\eta }}(v^{\prime };h)\}$. The choice of ω_e(v, v′; h) ensures the convergence of η̂(v; h₁). Specifically, if η_*(v) ≠ η_*(v′), then we have D_η(v, v′; h) = O_p(n^1/2) and K_st(D_η(v, v′; h)/C_n) converges to infinity and zero, respectively. Therefore, ω_e(v, v′; h) can give a small weight to voxel v′. Similar to the proof of Theorems 1–3 in [43], we can show that as n → ∞, η̂(v; h) converges η_*(v) and $\sqrt{n}\{\widehat{\mathit{\eta }}(v;h)-{\mathit{\eta }}_{\ast }(v)\}=O_p(1)$. Finally, we can prove Step (ii) for any fixed S.