Three-dimensional differential interference contrast microscopy using synthetic aperture imaging

Abstract.

We implement differential interference contrast (DIC) microscopy using high-speed synthetic aperture imaging that expands the passband of coherent imaging by a factor of 2.2. For an aperture synthesized coherent image, we apply for the numerical post-processing and obtain a high-contrast DIC image for arbitrary shearing direction and bias retardation. In addition, we obtain images at different depths without a scanning objective lens by numerically propagating the acquired coherent images. Our method achieves high-resolution and high-contrast 3-D DIC imaging of live biological cells. The proposed method will be useful for monitoring 3-D dynamics of intracellular particles.

1. Introduction

Differential interference contrast microscopy techniques visualize a specimen of weak contrast by converting the field gradient of a light into intensity variation. It has served as a label-free tool to image biological specimens.^1,2 However, the intensity in the DIC image is determined by the coupling of the amplitude and phase of the light field, and its response is nonlinear with respect to optical path length gradient. Therefore, the retrieval of the phase delay, which contains the quantitative information of the sample such as the thickness and drymass, is not straightforward and the technique is attributed as qualitative. Another drawback is that the structures in line with the shearing direction are not well visualized. Therefore, structures of interest have to be observed at the time of the experiment with proper setting of shearing direction. In addition, either an objective lens or a specimen has to be scanned along the axial direction to obtain images at different depths of focus. In order to overcome these limitations, various ways have been devised to obtain a quantitative phase map from DIC microscopy, such as controlling phase retardation and recording multiple images.^3–5 Although these approaches are time-consuming for acquiring multiple images, post-processing is available to choose the shearing direction depending on the target structures. But the numerical propagation of the recorded field is not available in these methods such that the need for objective lens scanning still remains for the 3-D imaging.

The innate drawbacks of DIC microscopy mentioned above can partly be solved by directly recording the amplitude and phase of the light field containing the sample image by using either digital holography or phase-shifting interferometry. Through these techniques, the amplitude and phase of the light field containing the sample information can be directly measured and then the acquired image can be processed into DIC image to enhance the contrast of the image.^6,7 Through image processing, shearing direction can be chosen arbitrarily and 3-D imaging can be achieved with the numerical propagation. But these coherent techniques have low spatial resolution and inherent diffraction noise compared to the incoherent imaging. This is why image quality is not comparable to that of DIC microscopy. There have been efforts to use a partially coherent source to acquire a high quality complex field image. But the refocusing of the measured complex field to a different depth based on the use of paraxial approximation is limited to the source of relatively high spatial coherence.^8,9 This poses a constraint in achieving 3-D imaging at a high spatial resolution.

Here we propose a method that combines synthetic aperture imaging and DIC microscopy to achieve 3-D imaging with high flexibility and high image contrast. To this end, we record multiple complex field images of a specimen at various angles of illumination and perform aperture synthesis of the recorded images to acquire a high-spatial resolution complex field image with suppressed diffraction noise. Then, we apply DIC algorithm for the synthesized image to acquire a high-contrast structural image. The recording of each complex field image at the known illumination wave makes it possible to apply the angular spectrum method¹⁰ for the precise propagation of the recorded field to a different depth. By the propagation of each complex field image and synthesis of the propagated angular images, we obtain high-resolution and depth-selective imaging without a scanning objective lens.

2. Methods

Aperture synthesis can provide a way to increase the illumination numerical aperture (NA).^11–19 It requires complex field images at several different angles of plane wave illumination with respect to the optical axis. By synthesizing the angular images, the passband in the spatial frequency can be enlarged by twice or more than that of the coherent imaging. For an incident field $U_{\mathrm{in}}(x,y)$ impinging onto an object, whose amplitude transmittance is $t(x,y)$, located at the front focal plane of an objective lens, the transmitted field becomes $U_o(x,y)=U_{\mathrm{in}}\times t$. Then, the field at the back focal plane of an objective lens, $U_f(u,v)$, is given as follows:

$$U_f(u,v)=\mathrm{circ}\left(\sqrt{\frac{u^2+v^2}{\mathrm{\Delta }\mathit{v}}}\right)\frac{1}{i\lambda f}\iint t(x,y)U_{\mathrm{in}}(x,y)\exp [-i\frac{2\pi }{\lambda f}(xu+yv)]\mathrm{d}x\mathrm{d}y,$$ (1)

where the circ function is introduced to represent the limited aperture of the imaging system, and $\mathrm{\Delta }v=f\mathrm{NA}$ with NA and $f$ being the numerical aperture and the focal length of the lens, respectively. For a normally incident unit-amplitude plane wave, the transmitted field is given as

$$U_f(u,v)=\frac{1}{i\lambda f}\mathrm{circ}\left(\sqrt{\frac{u^2+v^2}{\mathrm{\Delta }v}}\right)T(u/\lambda f,v/\lambda f),$$ (2)

where $T(u\lambda f,\hspace{0.17em}v\lambda f)$ is the Fourier transform of $t(x,y)$. In case of a plane wave with oblique incidence, $U_{\mathrm{in}}=\exp [-i2\pi (v_{x}x+v_{y}y)]$ whose wave vector is $2\pi (v_{x,}{v}_{y,}{v}_z)$, the transmitted field at the back focal plane is given as

$$\begin{gathered} U_f(u,v)=\frac{1}{i\lambda f}\mathrm{circ}\left(\sqrt{\frac{u^2+v^2}{\mathrm{\Delta }v}}\right)T(u/\lambda f+v_x,v/\lambda f+v_y) \\ \text{=\hspace{0.17em}}\frac{1}{i\lambda f}\mathrm{circ}\left[\sqrt{\frac{{(u-\lambda f{v}_x)}^2+{(v-\lambda f{v}_y)}^2}{\mathrm{\Delta }v}}\right]T(u/\lambda f,v/\lambda f). \end{gathered}$$ (3)

Note that the oblique incident plane wave shifts the aperture to a higher frequency band. Therefore, by synthesizing various illumination angles, we can effectively enlarge the passband and thus the numerical aperture. This results in the enhanced spatial resolution and the reduced depth-of-focus. As a consequence, the image can be clearer due to the rejection of the unwanted diffraction from out-of-focus plane.

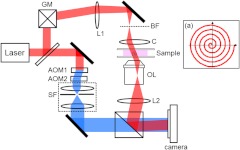
Recently, we developed high-speed synthetic aperture microscopy, which uses off-axis digital holographic microscopy for the fast recording of the complex field images and aperture synthesis for 3-D imaging of live biological cells. In this report, we use a Mach-Zehnder heterodyne interferometer^20,21 to acquire electric field ($E$-field) images at various illumination angles, and then synthesize in the scattering plane to increase the effective numerical aperture of illumination. The output of a He-Ne laser ($\lambda =632\mathrm{nm}$) is divided into sample and reference beams (Fig. 1). A dual-axis galvanometer mirror is positioned in the sample beam path to scan the direction of illumination. A lens ($L1$) and a high NA condenser lens (Nikon, 1.4NA) relay the reflected beam from the galvanometer mirrors onto the sample. The beam transmitted through the sample is imaged by a CMOS camera (Photron 1024PCI) using an objective (Olympus  UPLSAPO 100X,  1.4 NA) and a tube lens. In the reference beam path, two acousto-optic modulators (AOM1 and AOM2) are used to shift the frequency of the laser, and a spatial filter (SF) is inserted to improve the beam quality. A beamsplitter combines the sample beam and the frequency shifted reference beam to form an interferogram at the camera.

Fig. 1.

Synthetic aperture microscopy setup. Laser: He-Ne laser; GM: galvanometer scanning mirror, L1: $f=250\mathrm{mm}$ lens; BF: back focal plane of condenser lens; C: condenser lens; OL: objective lens; $L2$: tube lens, $f=200\mathrm{mm}$; AOMs: acousto-optic modulators; SF: spatial filter system. Frequency shifted reference laser beam is shown in blue. Inset: spiral trajectory of the focused spot at the BF.

To uniformly cover the NA of the condenser lens, we control dual-axis galvanometer mirrors such that the beam spot at the back focal plane of the condenser lens moves in a spiral pattern of five rotations as shown in Fig. 2(a). For a given angle of illumination, the camera records four images with a frame rate of 5000 fps, which is four times the frequency shift of the reference beam. The phase difference between consecutive images is $\pi /2$. By using phase-shifting interferometry, we obtain both phase, $\varphi (x,y)$, and amplitude, $A(x,y)$ of the field, from which the complex field, $E(x,y)=A(x,y)\exp \left[i\varphi \right(x,y\left)\right]$, is constructed. It takes about five seconds to record 360 angle-dependent $E$-field images.

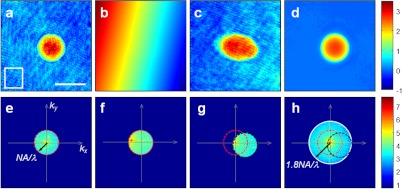
Fig. 2.

Angle-dependent complex field images and an aperture synthesized image. (a, e) Phase image taken in the image plane and the intensity distribution in the Fourier plane for zero-degree illumination. A 10 μm polystyrene bead is used as a sample. (b, f) Same as (a, e) for illumination angle of 50.9-deg. (c, g) Same as (b, f) after background subtraction. (d, h) Same as (a, e) but after aperture synthesis. Color bars indicate phase in radians for (a), (b), (c), and (d), and intensity in the logarithmic scale with base 10 for (e), (f), (g), and (h). Scale bar: 10 μm. Red and black circles in (e), (f), and (g) indicate passband with their radii corresponding to spatial frequencies of $\mathrm{NA}/\lambda$ and white circle in $h$ corresponds to $1.8\mathrm{NA}/\lambda$.

3. Results

A set of complex field images obtained at various angles of illumination is synthesized to increase the numerical aperture of the illumination. For illumination parallel to the optical axis of an objective lens, which is defined as illumination angle equal to zero, the phase image has a uniform background [see Fig. 2(a)]. By taking the Fourier transform of the E-field, we obtain the intensity distribution in the Fourier plane [see Fig. 2(e)]. The peak in the center of the Fourier plane is due to the unscattered light, which we call a direct current (dc) spot. It corresponds to zero spatial frequency analogous to direct current. The red circle indicates the limit of the passband with spatial frequency ${\mathrm{NA}}_{\mathrm{obj}}/\lambda$ where ${\mathrm{NA}}_{\mathrm{obj}}$ is the numerical aperture of the objective lens. For any non-zero angle of illumination, there is a linear phase ramp in the image plane as seen in Fig. 2(b). The dc spot in the Fourier plane is now shifted away from the center due to the tilt [see Fig. 2(f)], which is associated with the phase ramp in the image plane. As stated at the first line of Eq. (3), the passband remains the same since the objective lens is fixed while the angular spectrum of the object is shifted.

We now describe our method of synthesizing multiple angle-dependent images. The dc spots of various angular illuminations [for example, in Figs. 2(e) and 2(f)] represent a scattering angle of zero. In order to superpose multiple angular images, we shift the dc spot of non-zero degree illumination to the center in the Fourier plane. This is explicitly shown in the second line of Eq. (3). To perform this shifting operation, we first normalize the E-field image with a background image taken in the absence of the sample [Fig. 2(c)]. Then, the phase ramp is removed and the dc spot moves to the center in the Fourier plane. As a result, the circle defining the passband (the red dashed line) also shifts to the center of the Fourier map (the black dashed line). We repeat the same procedure for all the angular images. We then create a synthesized image by adding them all together. The resulting synthesized field is the summation of Eq. (3) for various incident wave vectors $({\nu }_x^i,{\nu }_y^i,{\nu }_x^i)$ as follows.

$$U_f(u,v)=\sum _i^{}\frac{1}{i\lambda f}\mathrm{circ}\left[\sqrt{\frac{{(u-\lambda f{v}_x^i)}^2+{(v-\lambda f{v}_y^i)}^2}{\mathrm{\Delta }v}}\right]T(u/\lambda f,v/\lambda f)\mathrm{.}$$ (4)

The white circle in Fig. 2(h) indicates the new passband after synthesis, which is enlarged in diameter compared to the original passband defined by the NA. This means that the sampling frequency has increased by about a factor of two in the scattering plane compared to the zero-degree illumination case. The actual increase is a factor of 1.8 in Fig. 2(h).

When adding the set of angular images, it is important to synchronize the phase between different images. In other words, the phases of dc spots from various angular images are to be synchronized. Otherwise, the phase of the synthesized image is deteriorated and phase map cannot be retrieved. This is especially important for imaging biological cells because they are mostly phase objects. We choose an area outside of the specimen [a white square box in Fig. 2(a)] and set the average phase of the area to be the same for all the complex field images. After adding all the complex field images, we have the resulting phase image [Fig. 2(d)]. The fixed pattern diffraction noises present in the individual angular images are removed and a high quality phase image is acquired. This is because the increase of the illumination NA rejects the out-of-focus images by reducing the depth-of-focus.

Next, we apply our technique for imaging biological cells. Figures 3(a) and 3(b) show amplitude and phase images of a HeLa cell obtained at zero degree illumination. In both images, many diffraction rings are present, especially around small particles. By contrast, the amplitude and phase of the synthesized image [Figs. 3(c) and 3(d)] show that the fixed pattern noise is effectively removed, thus presenting an image of high quality and low noise. Phase noise in the background is only 12% for the synthesized phase image in comparison with the single phase image.

Fig. 3.

Amplitude and phase images of live HeLa cells taken with illumination at 0-deg. (a, b) and acquired by synthetic aperture method (c, d). Amplitude in arbitrary units and phase in radians. Scale bar: 10 μm.

Aperture synthesized images differ from conventional coherent images in two respects. First, due to the coherent synthesis of the angular complex field images, the signal passband is expanded to about twice the extent of the coherent imaging. Second, digitized recording of the complex field enables post-processing, such as contrast enhancement and 3-D visualization. Here, we apply image processing method of DIC microscopy to enhance the contrast. Conventional DIC microscopy visualizes the gradient of the bright field image by optically interfering the original image with the spatially shifted image. Optics such as the Nomarski prism and polarizers are required to shift the original image, and the magnitude and direction of shifting together with the bias retardation are critical for optimal contrast. To get the fine details at various axial locations, either the objective lens or the specimen should be scanned. The drawback is that all the adjustments have to be made at the time of experiment. On the contrary, our method of post-processing the synthesized complex image can lead us to overcoming this drawback, because we can optimize contrast at an arbitrary shearing direction and depth.

For a given synthesized complex field, $E(x,y)$, we generate a synthesized DIC image, $I_{\mathrm{DIC}(x,y)}$, following the equation

$$I_{\mathrm{DIC}}(x,y)={|E(x,y)-E(x+\mathrm{\Delta }x,y+\mathrm{\Delta }y)e^{i\mathrm{\Phi }}|}^2,$$ (5)

where $\mathrm{\Delta }x$ and $\mathrm{\Delta }y$ are the shift of the image in $x$ and $y$ directions, respectively. The bias retardation is $\mathrm{\Phi }$ between the original complex field and the shifted field. The contrast of the DIC image can be controlled by this bias retardation. We can choose arbitrary shifting direction by controlling $\mathrm{\Delta }x$ and $\mathrm{\Delta }y$ depending on the structure. Figure 4(d) presents $I_{\mathrm{DIC}}$ for the same image shown in Figs. 3(c) and 3(d), with $\mathrm{\Delta }x=300\mathrm{nm}$, $\mathrm{\Delta }y=0\mathrm{nm}$, respectively, for the bias phase of $1/10\mathrm{rad}$. Many details, such as the nucleus, nucleolus, and small vacuoles, that were not clear in the original $E$-field image are clearly visible now. We obtain synthesized images after propagating individual angular images down to 2 μm toward an objective lens with the method to be described below and obtain DIC images at two orthogonal shearing directions [Figs. 5(a) and 5(b)]. The fine structures shown in the $y$-sheared image [the red arrow in Fig. 5(a)] is not shown in Fig. 5(b) because the structure is parallel to the $x$-axis Opposite is the case for the structure indicated by a blue arrow. This shows the strength of aperture synthesis in post-processing.

Fig. 4.

Gradient images acquired after numerical propagation. (a, b, and c) Images propagated by 6, 4, and 2 µm above the original focus. (d) Original focus. (e, f) Images propagated downward by 2 and 3 µm the bottom of the cells. Scale bar: 10 µm.

Fig. 5.

Numerical implementation of DIC by digital post-processing. (a) Shearing in $y$-direction by 300 nm. (b) Same as (a) but in $x$-direction. A red-arrow indicates a structure visible only for $y$-directional sheared image (a) while a solid blue arrow for $x$-directional sheared image (b). Scale bar: 5 μm.

In addition to the contrast enhancement, we also implement depth-selective visualization by angular spectrum method (Chapter 3 in Goodman).¹⁰ Conventional holography and quantitative phase microscopy have the ability to image in 3-D by the propagation of the field.²² But their axial resolution is poor because only 2-D information is recorded in the first place. Thus, a single-phase image cannot provide highly detailed images at various depths. On the other hand, conventional bright field or DIC microscopy is capable of acquiring depth-selective imaging due to high illumination and collection NAs but can monitor only one depth for a given objective focus.

Our method presents merits of both quantitative phase microscopy and DIC microscopy: depth-selective 3-D imaging. We numerically solve the propagation for each of the angular complex field images to a certain distance from the objective focus, and synthesize a set of propagated complex field images again to form a highly depth-selective image. Figure 4 presents depth-selective images as we vary the propagation distance. Figure 4(d) is the image taken at the original objective focus, and Figs. 4(a)–4(c) are the images propagated by 6, 4, and 2 microns above the original focus. As the focus moves toward the top part of the cell, multiple nucleoli appear and the cell body is shrunk. Figures 4(e) and 4(f) are the propagated images below the original focus by 2 and 3 microns, respectively. The bottom part of the cells appear and fine structures, such as the filopodia, become clearly visible. This demonstrates that small depth-of-focus 3-D imaging is acquired without objective scanning.

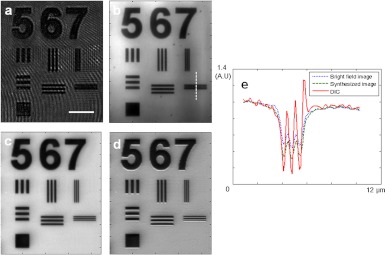
In our previous publication,²³ we demonstrated that the aperture synthesis improves the spatial resolution of the coherent image from the diffraction limited resolution of 550 nm $(1.22\lambda /1.4)$ to the enhanced resolution $(1.22\lambda /2.2=350\mathrm{nm})$ In addition to the spatial resolution enhancement, we apply the numerical DIC analysis on the synthesized coherent image to further enhance the image contrast. We generate the pattern of a U.S. Air Force target-like phase pattern on a spatial light modulator (Holoeye, LC-R 2500) with half pitch of the stripe patterns under numbers 5, 6, and 7, corresponding to 1200 nm, 800 nm, and 400 nm, respectively. Figure 6(b) is a bright field image, i.e. an incoherent summation of angular images, and Fig. 6(c) is a synthesized image. Both the images present the resolution enhancement in comparison with the single coherent image [Fig. 6(a)], but the latter has slightly better contrast. This is because the bright field analysis undergoes a decrease of modulation transfer function at high spatial frequencies while the aperture synthesis has the flat spectral response. In addition, the synthesized image is coherent in that it can be processed into a DIC image. Figure 6(d) shows the processed DIC image. It is obtained after 86 nm of shearing along the vertical direction with phase retardation of $\pi /15$ radian. This additional post-processing further increases the contrast of the image. Specifically, the profile along the line indicated in Fig. 6(e) shows a much clearer modulation of the structures in comparison with the bright field or synthesized image.

Fig. 6.

Enhancement of image contrast by the post-processing. (a) Single coherent image (b) bright field analysis. (c) Aperture synthesized image. (d) DIC image of (c) at shearing distance 86 nm. (e) Line profile of each image along the white-dashed line indicated in (b). Scale bar, 10 µm.

Quantitative phase imaging with a partially coherent illumination source can also provide depth-selective imaging. But it does not provide 3-D imaging unless the objective focus is scanned. We next explain the necessity of collecting multiple angular images for 3-D imaging as well as for depth-selective imaging. In the case of using a partially coherent illumination source for the phase imaging, the measured complex field is the change made by an object, not the complex field at the sample plane. The illumination wave is either cancelled by a reference wave or averaged out in time. Therefore, the Fourier transform of the measured complex field does not correspond to the angular spectrum at the sample plane. This means that the angular spectrum method cannot be applied for the refocusing. For this reason, the partially coherent imaging provides only depth-selective images, not 3-D imaging. For the depth-selective, 3-D imaging, we need to have precise knowledge of the illumination wave, i.e. the angular plane wave in our method. In fact, we have published a work that uses dynamic speckles with extremely low spatial coherence in off-axis digital holography.²⁴ In this case, the numerical propagation by the angular spectrum method did not work at all because the measured field was not the actual field at the sample plane, but the average of the change induced by the specimen. It may be worthwhile to construct a rigorous mathematical framework that works for a source of extremely low spatial coherence in a future study.

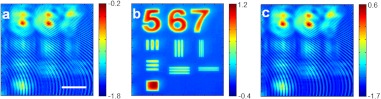
In order to elucidate the necessity of knowing the illumination wave for 3-D imaging, we compare the two cases: synthesis after propagating each angular image, and the propagation of the synthesized image. Figure 7(a) shows the synthesized image of a target object at the original focus, which is away from the object plane by 7 μm The object structures are blurred due to the defocusing. We then obtain the synthesized image after the propagation of each angular image by 7 μm [Fig. 7(b)]. The refocusing to the object plane works well, and the fine structures of the object are clearly visible. But when we apply the angular spectrum method directly to the synthesized image taken at the original focus, then the refocusing does not work at all [Fig. 7(c)]. In other words, the angular spectrum method is not applicable to the synthesized image because the spectrum of the synthesized image does not correspond to the angular spectrum at the sample plane. In order to achieve both depth-selective and 3-D imaging, it is necessary to take multiple angular images and to propagate individual angular images separately.

Fig. 7.

Comparison between the synthesis after the propagation of each angular image and the propagation of a synthesized image. (a) Phase part of the synthesized image at the original focus. (b) Same as (a) but each angular image is propagated by 7 µm. (c) Direct application of angular spectrum method for the synthesized image taken at the original focus. Color bar, phase in radians. Scale bar, 10 µm.

4. Conclusion

We presented the emulated DIC microscopy using high-speed synthetic aperture microscopy featuring the enhanced spatial resolution and reduced noise in comparison with conventional quantitative phase microscopy. In doing so, we could maintain merits of both DIC microscopy and coherent imaging: 3-D and high-contrast imaging. This technique will lead to the high-speed and high-resolution volumetric imaging of biological cells.