Multiscale natural moves refine macromolecules using single-particle electron microscopy projection images

Abstract

The method presented here refines molecular conformations directly against projections of single particles measured by electron microscopy. By optimizing the orientation of the projection at the same time as the conformation, the method is well-suited to two-dimensional class averages from cryoelectron microscopy. Such direct use of two-dimensional images circumvents the need for a three-dimensional density map, which may be difficult to reconstruct from projections due to structural heterogeneity or preferred orientations of the sample on the grid. Our refinement protocol exploits Natural Move Monte Carlo to model a macromolecule as a small number of segments connected by flexible loops, on multiple scales. After tests on artificial data from lysozyme, we applied the method to the Methonococcus maripaludis chaperonin. We successfully refined its conformation from a closed-state initial model to an open-state final model using just one class-averaged projection. We also used Natural Moves to iteratively refine against heterogeneous projection images of Methonococcus maripaludis chaperonin in a mix of open and closed states. Our results suggest a general method for electron microscopy refinement specially suited to macromolecules with significant conformational flexibility. The algorithm is available in the program Methodologies for Optimization and Sampling In Computational Studies.

Recent advances in single-particle cryoelectron microscopy, or cryo-EM, have enabled 3D structure determination of macromolecules to near-atomic resolution without crystallization, provided that the sample particles are homogeneous and adopt the same conformation (1–6). However, macromolecules are generally flexible in solution and can adopt multiple conformations in order to carry out their functions. Therefore, their cryo-EM images usually represent a heterogeneous mixture of macromolecular conformations. As a result, the power of single particle cryo-EM is limited, in that the reconstruction of a high-resolution 3D density map requires hundreds of thousands to millions of particle images of the same conformation.

Supervised classification (7) and maximum-likelihood methods (8) have been used to identify multiple structures from samples in which macromolecules experience moderate conformational fluctuations or exist in a small number of discrete structural states. Other approaches based on statistical bootstrapping (9, 10) have been used to separate different substrate-binding modes of macromolecules or to define flexible fragments within a molecular complex. However, these single-particle image processing techniques are severely limited when there are large conformational changes or nondiscrete conformational states (11, 12) that prevent correct determination of the orientation parameters for each raw particle image. Various computational techniques have been developed to model large conformational changes by flexible-fitting of a molecular model into the density map of another conformation (13–18). However, all these modeling methods rely on the availability of a density map. In many cases, the structural flexibility and heterogeneity of the sample make it difficult to assign each projected image to the correct conformational state of the molecular complex. Without such assignment, all classical single-particle refinement procedures fail to determine the particle orientation parameters needed for reconstructing the 3D density map.

In addition, many protein complexes tend to prefer a particular orientation relative to the grid when frozen in vitreous ice for cryo-EM (4, 19). This tendency leads to a nonuniform angular sampling of the projections of the macromolecule that hampers a 3D density map reconstruction. To get a more uniform sample orientation distribution, detergent is usually added to the buffer. Unfortunately, this can cause side effects, such as uneven ice thickness and increased image background noise, that complicate sample preparation and image processing for single-particle cryo-EM. For samples whose amino acid sequences can be manipulated, exposed hydrophobic patches may be removed from the protein of interest so as to reduce preferred orientation on the grid (4). For macromolecules that are directly purified from an organism, their sequence cannot be changed. Therefore, this approach is not applicable (19).

In contrast, a 2D electron microscopy projection contains valuable information on the macromolecular conformation: Analysis of these 2D data provides a straightforward and robust computational approach that deals with sample flexibility and heterogeneity (20). By refining the macromolecular model directly against these projection data, one can bypass the need for a density map, avoiding the potential information loss due to averaging over different conformations. Nevertheless, the direct use of 2D images for refinement has not been fully explored for fear of overfitting the data due to the large number of macromolecular degrees of freedom (referred to as DOF).

Fortunately, molecular complexes can be decomposed into rigid domain segments connected by flexible loops. Their conformations can then be sampled using translational and rotational DOF of these domains (21). Use of such DOF may break the chains in the flexible loops necessitating solution of the chain-closure problem. Traditional analytical chain-closure algorithms (22–25) do not work on more than six chain-closure DOF because of their computational complexity. In contrast, our recently developed recursive stochastic chain-closure algorithm, which has linearly-increasing computational cost with number of variables, removes this technical barrier (26). As a result, one can use enough DOF to allow long connecting loops to be fully flexible. This increased conformational flexibility allows the relative arrangement of domain segments to be sampled more efficiently. The chain closure algorithm also allows one to freely select domain segments with DOF inferred from experimental observations. We refer to these DOF as natural moves.

In this study, we use natural moves to refine macromolecular models directly against 2D EM images, particularly the 2D cryo-EM class averages, which have higher signal-to-noise ratio. These class averages are obtained by first classifying raw particle images into different classes based on their mutual similarity using a multivariate statistical analysis approach, then aligning and averaging the raw particle images within the same class (see Materials and Methods). We developed a computational method to model the molecular conformations with hierarchical natural moves that are made progressively more detailed. The projection orientation parameters of the 2D EM image are also refined simultaneously. The robust search in conformational and projection orientation space is guided by Monte Carlo based optimization using a modulated temperature profile. The combination of Natural Move Monte Carlo (NM-MC) and temperature modulation uses a small number of essential DOF while reducing the chance of being trapped in local minima (see Materials and Methods).

This refinement protocol was applied to the Methonococcus maripaludis chaperonin (Mm-cpn), a protein machine that helps other proteins to fold in archaea (27). Mm-cpn molecules undergo large conformational changes during their functional cycle and can exist in a mixture of conformations under low ATP concentration (4, 28–31). Moreover, the open-state Mm-cpn exhibits a dominant end-on view in cryo-EM, making it an excellent benchmark for tackling the preferred orientation problem (4).

Results

Using Lysozyme-Simulated Data to Establish the Optimal Refinement Protocol.

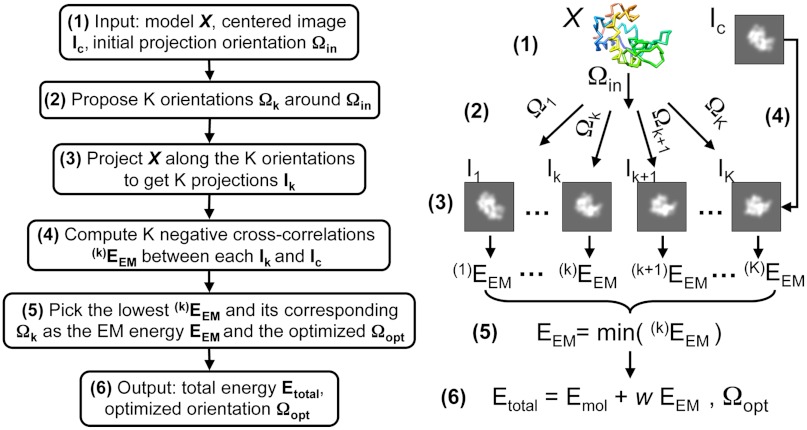
The goal of the present procedure is to change the structure of the starting model so as to maximize the similarity between the target 2D EM image and the projection of this new model. Here we use an EM energy defined by the negative cross-correlation between the target image and model projection to measure their similarity (Fig. 1, Figs. S1 and S2, and SI Materials and Methods). We exhaustively search the initial projection angle along with the in-plane shift parameters in order to optimize the match between the projection of the starting model and the target 2D EM image. This initial search can be done with any single-particle image processing software such as EMAN (32). We then translate the target image by these in-plane shift parameters to obtain the centered image I_c, which is then used as one of the inputs in our refinement. To ensure that the estimate of the orientation is optimal, we readjust these orientation parameters at every step of the refinement. This readjustment is achieved by introducing an energy function that is minimized with respect to orientation as illustrated in Fig. 1.

Fig. 1.

Obtaining the energy score of a model with an optimized orientation. The input orientation Ω_in is the Euler angle used to project the model, X. I_c is the centered target image, a constant parameter (step 1). A series of orientation angles Ω_k are generated around Ω_in (step 2, see SI Materials and Methods). The model X is projected along these proposed orientations to generate the corresponding projection images I_k (step 3). Negative cross-correlation scores 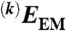are calculated between these projection images and the image I_c (step 4). The lowest value is assigned to the EM energy E_EM between the model X and the input image I_c (step 5). Its corresponding orientation is considered the optimized orientation Ω_opt that projects X to fit I_c. The outputs are the optimized projection orientation Ω_opt and the total energy E_total, which is the sum of a molecular energy, E_mol and the EM energy E_EM, weighted by an adjustable weight parameter w (step 6). E_mol is a function of the current model X to ensure its proper stereochemistry.

Next, the desired set of natural moves is constructed by the following steps: (i) Partition the given molecular assembly into several segments connected by flexible loops based on experimental observation or computational prediction (33). (ii) Assign rotational and translational DOF to each segment. (iii) Maintain loop continuity with our recursive stochastic chain-closure algorithm, which permits long connecting loops of any length and thus allows sufficiently free movement of the segments (26).

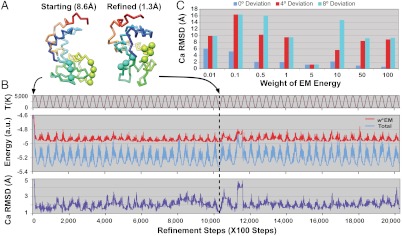
Here, lysozyme is modeled by three rigid segments connected by two flexible loops (Fig. 2A). In this ideal test case, we assume the major conformational changes of the lysozyme can be described with this natural move representation. Thus, an initial, deformed model with 8.4 Å C^α rmsd to the target structure was generated using these natural move DOF. We then refine this model against a projection of the target model.

Fig. 2.

Temperature-modulated NM-MC refinement protocol with lysozyme as an example. A total of 2.03 million steps of temperature-modulated NM-MC were carried out for each refinement. No noise was added to the target 2D image projected from the target structure. (A) Each lysozyme model is represented by three rigid segments connected by two flexible loops (residues 40–42 and 85–88 drawn as spheres). (B) The temperature, T (brown), the energy (EM in red, total in blue), and C^α rmsd (purple) from the target lysozyme structure are shown as a function of the refinement steps. The initial model (A, Left) has an 8.6 Å C^α rmsd to the target. The model with the lowest EM energy (obtained at the step indicated by a black vertical dash line) is much closer to the target structure (1.3 Å C^α rmsd, A, Right). In this example, the EM image has no noise or orientation estimate error and the weight of the EM energy is 5. (C) The best C^α rmsd each refinement can achieve with eight different weights for the EM energy (from 0.01 to 100, as marked along the x axis) and three different orientation errors: 0° (blue bars), 4° (red bars), 8° (cyan bars). In the presence of orientation errors, the optimum weight value of 5 yields the lowest C^α rmsd values.

In all refinement protocols, the NM-MC algorithm with a modulated temperature profile was used (see Materials and Methods). The annealing temperature, which is a sinusoidal profile with certain amplitude and frequency, facilitates rapid exploration of the conformational space by efficiently escaping from local energy minima (Fig. 2B).

In addition to the EM energy, one may optionally introduce a molecular energy based on a knowledge-based potential (34, 35). This new term helps avoid improbable conformations and collisions between different parts of the molecule. When the initial estimate of model orientation is not within the convergence radius of the correct orientation, it leads to an unreliable EM energy. In this case, incorporation of the molecular energy is essential to compensate for the inaccuracies in the EM energy. Combing the molecular energy, E_mol, and the EM energy,E_EM, we derived the total energy function, E_total = E_mol + wE_EM, which is used to guide our optimization protocol (step 6 in Fig. 1). Here, w refers to the weight that controls the contribution arising from the experimental EM data. Carefully choosing the weight to be between the molecular energy and the EM energy requires separate investigations; in the refinements done here, a range of weights were tested to find the optimum value that minimizes the final C^α rmsd between the refined model and the target structure. When the target structure is unknown, one can gradually increase the weight until the model shows bad stereochemistry. Whereas the refinement protocol is entirely driven by the total energy, the EM energy alone is used to judge the quality of the refined model.

Fig. 2B shows an example with a perfect initial estimate of the orientation. The refinement yields a resulting model with 1.3 Å C^α rmsd to the target structure. In Fig. 2B, the EM energy, total energy, and C^α rmsd fluctuate synchronously with the varying temperature; this suggests that our refinement escapes from local energy minima efficiently.

Fig. 2C shows a more difficult case where we introduce an initial orientation deviation with altitude angle θ = 0°, 4°, or 8°, respectively, and refine the orientation parameters accordingly. Given an accurate orientation, increasing the weight of the EM energy generally yields a better refinement result. This finding confirms the reliability of the EM energy when the correct orientation is used. While the molecular energy term prevents the occurrence of unphysical conformations (such as collision or overlap between segments), it may confine conformational search toward the initial model and reduce the conformational sampling efficiency. On the other hand, keeping a partial molecular energy term is useful when there are errors in the orientation estimate: When θ = 4° or 8°, refinement with weight w = 5 performed best in this case.

Using Multiscale Natural Moves to Refine the Mm-cpn.

Mm-cpn is a 16-subunit homo-oligomeric chaperone from the mesophilic archaea. It helps other proteins fold correctly in archaea cells. It consists of two back-to-back rings of eight subunits. Each subunit has a substrate-binding apical domain, an ATP-binding equatorial domain, and an intermediate domain connecting the apical and equatorial domains. Mm-cpn closes its folding chamber upon ATP hydrolysis and reopens it after the γ-phosphate is released. The entire complex is approximately 1 MDa in size, and the opening and closing of the ring is achieved mostly through a rigid-body rocking of individual subunits (4, 29, 31). In EM images of the open state of wild-type Mm-cpn, most particles take up an end-on view orientation on the grid; this makes reconstruction of a 3D density map very difficult (4). Under low ATP concentration, Mm-cpn exists in various conformational states as each subunit is conformationally flexible in the open form (30).

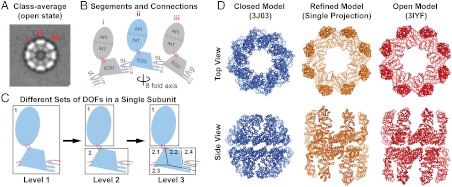
The large size (more than 8,000 residues) and substantial conformational change (approximately 16 Å C^α rmsd) between the open and closed states of Mm-cpn make it a challenge for conventional refinement. It is, however, a perfect benchmark for our multiscale NM-MC refinement procedure. Here, we use the lidless variant of Mm-cpn so as to avoid the potentially unstructured protruding lid segments in the open state. Compared to the wild-type, lidless Mm-cpn provides a higher resolution EM open structure (4), which can be used to further verify our refinement. The initial model was chosen as the Protein Data Bank (PDB) structure 3J03 of the ATP/aluminum fluoride induced lidless Mm-cpn in the closed state (31). We refine it against a top-view class average (Fig. 3A) that was generated from 228 raw particles of the ATP-free lidless Mm-cpn (see Materials and Methods). This class average contains real noise, and its initial orientation parameters relative to the initial model are estimated as ϕ = 22.5° in-plane rotation around its eightfold symmetry axis. The refinement is carried out with no assumed symmetry, and the orientation parameters are also optimized during refinement.

Fig. 3.

Lidless Mm-cpn model refined against a single cryo-EM projection class average. (A) Top view of the projection class-average image in the open state. Three subunits are labeled, and the projection orientation is estimated to be rotated by 22.5° in-plane relative to the initial model. (B) Schematic definition of the segments and their connecting loops (solid red lines) of lidless Mm-cpn showing the three subunits from (A). Neighboring subunits are colored grey and blue, respectively. The stem loop of one subunit is hydrogen bonded with the NC termini of the other, as indicated by dotted red lines. The viewing angle is from the eightfold symmetry axis. (C) Three levels of region compositions for a single subunit with hierarchically increasing DOF. (D) Top and side views of the initial model from PDB id 3J03 (blue), the refined model (orange), and the map-derived model from PDB id 3IYF (red). Eighty thousand temperature-modulated NM-MC steps were carried out successively for each of the three levels to refine the initial model against the 2D cryo-EM class average (Fig. S3 and Movies S1–S3). The model with the lowest EM energy during the previous level of refinement was used as the initial model for the next level.

Fig. 3B shows how we define the segments and connections in the Mm-cpn. In each Mm-cpn subunit, the apical and intermediate domains form a segment (API/INT) due to the salt bridges between them (4). The equatorial domain without the stem loop forms the second segment (EQU). The stem loop itself forms a third segment (SL). Loop connectivity is always maintained between these segments (solid red loops). The entire 16-subunit Mm-cpn complex contains 48 segments. In the multiscale natural move refinement, we group these segments (whether or not in the same subunit) into different sets of “regions” with each region having three translational and three rotational DOF. This grouping involves three hierarchical levels, allowing finer description of conformational changes (Fig. 3C).

• Level 1: All the segments within the box are grouped into a single rigid region; chain breaks can occur between the SL and the EQU of the same subunit. The entire Mm-cpn complex is treated as 16 rigid regions to capture the overall rocking of the subunit while maintaining the interaction between adjacent subunits through the SL and NC termini (4).

• Level 2: The API/INT segment in a subunit forms rigid region 1; EQU in a subunit and SL of the neighbor form rigid region 2. In one subunit, chain closure can occur between the SL and EQU as well as between the API/INT and the EQU. The entire Mm-cpn complex contains 32 rigid regions to capture the overall subunit rocking and the motion between the equatorial and intermediate domains.

• Level 3: Starting from level 2, we divide region 2 into four subregions: 2.1, 2.1, 2.3, and 2.4. All subregions within the box remain connected by chain closure but have their own rotational and translational DOF describing more subtle conformational fluctuations around the ATP-binding pocket.

Fig. 3D shows the starting model, the final refined model after three levels of refinement (Fig. S3 and Movies S1–S3, and the open-state model (PDB ID: 3IYF) built into a 3D density map at 8 Å resolution. Our final model refined against just a single 2D cryo-EM class average is very similar to the model built from the 3D density (C^α rmsd of 5.7 Å). As noted, the density-derived model is built from a cryo-EM map (accession number EMD-5140), which was reconstructed with D8 symmetry, while our refined model does not assume any symmetry. After blurring our refined model to a density map at 8 Å resolution with D8 symmetry imposed, the density of our refined model has a cross-correlation score of 0.95 with respect to the cryo-EM map (Fig. S4).

Separating Heterogeneous Conformations of Mm-cpn in Mixed Open and Closed States with Iterative NM-MC Refinement.

Given the closed-state Mm-cpn as an initial model, the method presented here was used to classify an artificially constructed set of 10,000 heterogeneous particles of Mm-cpn in mixed open and closed conformations from experimental images (Fig. 4A). First, 2D analysis was applied to generate 100 class averages, each of which represents a conformation viewed at a particular orientation (Fig. 4B and Fig. S5). The 2D analysis was followed by iterative NM-MC refinement against each of the class averages to generate their corresponding 3D models (see Materials and Methods, and Figs. S6 and S7). Fig. 4C shows the refinement results for six representative class averages with different orientations and conformations. By clustering the 100 refined models, two conformational populations of the Mm-cpn were identified. These clustered models within each population were averaged and blurred to two seed electron density maps at 30 Å resolution to initialize additional EM data processing and map reconstruction against the 10,000 raw particle images. In the end, two 9 Å-resolution maps were obtained that showed α-helices clearly (Fig. 4D, and Figs. S8 and S9).

Fig. 4.

Separating heterogeneous conformations of lidless Mm-cpn with mixed states of EM particle images using the closed-state initial model. (A) Mixing 5000 ATP/aluminum fluoride-induced (closed) and 5000 ATP-free (open) states of lidless Mm-cpn raw particle images to generate the artificial heterogeneous EM dataset of 10,000 particles. (B) The 100 2D class averages that were generated from the 10,000 particle images. (C) Refinement results against six representative class averages exhibiting various conformational and orientational states such as open side view (Average #0), closed tilted view (Average #4), open top view (Average #30), closed side view (Average #51), closed top view (Average #88), and open tiled view (Average #96). Column I shows the projections of the initial closed-state model along the initially estimated orientations. Column C shows the target 2D experimental class averages. Column R shows the projection of each refined models (Column M) along the refined orientations. Column M shows the refined models after three iterations of NM-MC refinement (Materials and Methods). Note that for Average #30, the initially estimated orientation was not correct due to the large conformational difference between the initial model and the class average. After three iterations, both the correct orientation and conformation were obtained. (D) Seed maps generated from two clustered states of the refined models at 30 Å resolution (Left) and the re-refined maps at 9 Å resolution in which α-helices are visible (SI Materials and Methods, Figs. S8 and S9).

Discussion

Robustness of the EM Energy.

We find that the EM energy, which is defined as the negative cross-correlation between the target image and the model projection, is selective enough to refine the model against EM projection images with signal-to-noise ratios similar to those found in a 2D class average (SI Materials and Methods and Fig. S1). In spite of the inaccuracies in the scaling factor or center estimate for the target images (from errors introduced when calibrating the microscope magnification or determining the image shift parameters), the EM energy is still able to pick structures with small C^α rmsd (Fig. S2). We do find that with an image noise level similar to that in an unaveraged raw cryo-EM image (Fig. S1), the EM energy is no longer good for refinement. It is possible to cluster models against multiple projection images of similar conformations in different orientations to improve the consistency of the refinement result, as shown in Fig. 4C and Figs. S6 and S7. To improve accuracy, we followed an iterative approach. One may also refine the model using a combined EM energy score from several projection images of the same conformation at different orientations.

Cross-Validation of the Refinement Results.

The use of 2D class average as the target image allows convenient cross-validation of the refinement results. We subdivide the 228 raw particle images of Mm-cpn initially used to generate the single top-view class average images into two groups to generate two different subclass average images. Each subclass average image can be independently used to refine the initial model with the same protocol. In the case of Mm-cpn, these two resulting models have a C^α rmsd of 5.8 Å between them, which indicates the refinement consistency (Fig. S10). Their C^α rmsd values from the refined model against the target 2D class average projection (Fig. 3D, Middle) and the model built from the 3D density (Fig. 3D, Bottom) are 5.9 and 5.8 Å and 6.3 and 6.3 Å, respectively.

Potential Application for EM Data with Preferred Orientation.

In many single-particle cryo-EM studies, the molecules tend to be frozen in one particular orientation. This limitation in angular sampling is a major obstacle to generating a 3D density map. Our method avoids fitting into a 3D density map and directly refines against 2D class averages; therefore, it does not suffer from this limitation. In the example of Mm-cpn, we have successfully refined the model against a top-view 2D class average, which represents the preferred orientation of the sample on the grid.

Conclusions

The EM energy introduced in this study can be used to refine a 3D molecular model and its orientation parameters directly against EM projection images, particularly cryo-EM class average images that benefit from high signal-to-noise ratio. An additional molecular energy term may be used together with the EM energy to compensate for inaccurate estimate for the initial orientation parameters. As shown by the simulated data derived from lysozyme and real data on Mm-cpn, the use of natural moves in temperature-modulated Monte Carlo greatly facilitates the search for the correct model conformation and orientation. To model the large conformational change of Mm-cpn, we use natural move DOF at multiple scales. Fewer DOF from a larger regions are required at the beginning to describe large structural deformations, while more detailed DOF from smaller regions are used later to model more subtle conformational changes. In the example of Mm-cpn, we show that it is possible to refine the conformation of a large molecular complex with a preferred end-on orientation on the grid, suggesting an approach to deal with the preferred orientation problem in single-particle cryo-EM. We demonstrate that, by using the iterative NM-MC refinement procedure, it is possible to separate heterogeneous EM particles to generate higher-resolution density maps. By adapting the current approach to simultaneously optimize the model conformation and its orientation with respect to the subtomogram containing the “missing wedge,” we hope that our NM-MC refinement can aid in the separation of conformational heterogeneity in studies using cryoelectron tomography and 3D subvolume averaging as well (36).

Materials and Methods

Using Multiscale Natural Move Monte Carlo.

Markov Chain Monte Carlo-based refinement of large macromolecular structure is usually hampered by two major obstacles: the large number of DOF and the complex topology of the scoring function. To overcome the problem of a large number of DOF, we propose different sets of DOF, referred to as levels (Fig. 3). In each level, segments of a macromolecule can be grouped into different regions that can independently translate and rotate to generate a new conformation or configuration of the regions. Each proposed configuration of these regions may cause chain break(s) and is thus followed by a chain-closure procedure (26) to ensure the proper geometry of the connecting loops. The resulting proposed conformation is scored by the energy function, E_total. The refinement procedure is guided by a multi-scale temperature-modulated NM-MC protocol, where the overall set of DOF changes so that the total number of DOF progressively increases. In particular, Fig. 3C illustrates the three sets of DOF used to refine the Mm-cpn models. To effectively overcome limitations arising from the complex topology of the scoring function, the NM-MC utilizes a periodically fluctuating temperature profile so that all the essential energy basins are rapidly explored. This protocol is implemented in the software package Methodologies for Optimization and Sampling In Computational Studies (37).

We find that the use of gradually more detailed DOF is necessary for proper refinement (Fig. S11). If we skip level 1 and directly run the refinement with only the EM energy at level 2, the resulting model gets trapped in a local energy minima in which subunits collide. Introducing additional molecular energy prevents the subunit collision, but the resulting model is still distorted. Therefore, our control calculation suggests that using very few DOF at the beginning can help bypass many energy barriers and aid convergence to the correct model. At later stages, more detailed DOF may be used to further explore local conformational states.

Starting Model and 2D Class-Average Image Generation, Map Conversion and Calculation, Figure and Movie Productions.

To use a reduced-model knowledge-based potential, residues in the macromolecule were represented by a three-point model that consists of the C^α, carbonyl O atoms, and a centroid for the side chain. To establish the optimal refinement protocol using the lysozyme-derived artificial data, another starting model in Fig. 3 with 8.4 Å C^α rmsd was generated by 25,000 steps of Monte Carlo at 300,000 K using the DOF defined in Fig. 3A. Two-dimensional class averages of Mm-cpn were generated using program refine2d.py in the EMAN software (32). Map conversion from PDB and map low-pass filtering were performed using the pdb2mrc command and the proc3d command in EMAN, respectively. Figures and movies were generated using University of California San Francisco (UCSF) Chimera (38). The cross-correlation between the model-converted map and the cryo-EM map (EMD-5140) was calculated with the Chimera fit-in-map function.

Iterative NM-MC Refinement Against Multiple Heterogeneous Particle Projections.

To refine the closed-state initial model against the 100 class-averages of Mm-cpn with mixed conformations, we used only the EM energy and level 1 DOF as defined in Fig. 3C. To reduce the computational cost, these class averages were shrunk fourfold relative to the original image size. To generate their corresponding 3D models (Fig. 4C and Fig. S6), NM-MC refinements were carried out against each of the class averaged target images. When comparing and clustering all these resulting models, we identified different conformational populations by measuring the “openness” of the central folding chamber of Mm-cpn (Fig. S7). The PDB coordinates of the clustered models within each population were averaged and used to reestimate the initial orientation parameters of each projection for another round of NM-MC refinement. To improve the refinement results, this procedure was carried out for three consecutive iterations having 20,000, 80,000, and 80,000 steps, respectively. The clustered and averaged refined model from the previous iteration was used as the initial model of the following iteration. For each class average, 20,000 steps of NM-MC refinement took about 1 h on a single core of the Bio-X2 cluster.

EM Image Processing and Map Reconstruction Using Two Seed Maps.

The averaged models within each of the two final clusters of Mm-cpn were blurred to give two seed electron density maps at 30 Å resolution using the pdb2mrc command in EMAN. These two seed maps were then used to initialize additional EM data processing and map reconstruction using the original 10,000 raw particle images with the multi-refine command in EMAN. D8 symmetry was imposed to achieve higher resolution out of a limited number of particles.