Hydrodynamic trapping of molecules in lipid bilayers

Abstract

In this work we show how hydrodynamic forces can be used to locally trap molecules in a supported lipid bilayer (SLB). The method uses the hydrodynamic drag forces arising from a flow through a conical pipette with a tip radius of 1–1.5 μm, placed approximately 1 μm above the investigated SLB. This results in a localized forcefield that acts on molecules protruding from the SLB, yielding a hydrodynamic trap with a size approximately given by the size of the pipette tip. We demonstrate this concept by trapping the protein streptavidin, bound to biotin receptors in the SLB. It is also shown how static and kinetic information about the intermolecular interactions in the lipid bilayer can be obtained by relating how the magnitude of the hydrodynamic forces affects the accumulation of protein molecules in the trap.

Much research has been focused on different methods to trap and manipulate molecules and small particles in three dimensions. This requires that the energy of the molecules is decreased in the region of the trap and that the potential energy is sufficiently low to dominate over thermal fluctuations. Examples of how this has been achieved include: magnetic (1) and electric (2–4) fields, optical traps (5, 6) and acoustic waves (7). Despite the extensive use of these techniques to trap molecules in solution, a general molecular trap to capture and hold molecules locally in a cell membrane or lipid bilayer is still lacking. Such a method would be interesting for several reasons. For example, it could yield information about the local mobility and organization and be used to study intermolecular forces between different membrane-associated molecules, information that is currently hard to obtain experimentally.

There are several reasons why trapping molecules such as membrane proteins in a lipid bilayer is difficult with the methods that exists today. One is the small size of the individual molecules (approximately 10 nm), compared to the size of particles usually trapped by magnetic and optical tweezers in biological applications (100–1000 nm) (8). Another complication is the similar material properties, such as refractive index, that many membrane-associated molecules have. This can make trapping of molecules based on the difference in material properties to its surroundings difficult. Cohen et al. showed trapping of individual molecules in solution using electrokinetic feedback controlled by tracking of the trapped and fluorescently labelled molecules (3). A drawback with this technique is that the trapped molecules need to be tracked all the time, which makes it susceptible to photobleaching. Another example where electric fields have been used to trap small particles was shown by Krishnan, et al. who utilized the electric field distribution around nanometer-sized topographic features to trap approximately 100 nm-sized charged particles in a low-salt solution (4). However, the extension to trap molecules in a lipid bilayer is not trivial.

In this work, we show how the forces from a liquid flow into a conical pipette can be used to locally trap protein molecules bound to a lipid bilayer. This was demonstrated by trapping the approximately 5-nm large protein streptavidin (SA) bound to biotin receptors in a supported lipid bilayer (SLB). An SLB is a lipid bilayer formed on a solid support, such as a planar glass slide (9, 10). SLBs are commonly used cell membrane mimics and display many of the properties of a cell membrane, including the lateral fluidity, and have the advantage of having a controllable molecular composition and being relatively easy to study. However, the presented technique is in principle not limited to a planar SLB, but could be used on any lipid bilayer that can be approached by a pipette as long as the deformation of the studied lipid bilayer due to the liquid flow is small.

Model

Principle of the Method.

The mechanism behind the hydrodynamic trap is shown in Fig. 1. A conical glass pipette, with an inner tip radius of approximately 1 μm, is first positioned approximately one tip radius above the SLB (Fig. 1A). This is made by simultaneously lowering the pipette towards the surface, using a piezoelectric positioning system on which the pipette is mounted, and measuring the ion current between an electrode in the pipette and an electrode in the surrounding bath. The ion current decreases as the pipette is brought closer to the surface and when the distance between the pipette and the SLB is of the order of one tip radius the current through the pipette has been reduced by roughly 1% (11). This is also the mechanism used for scanning ion conductance microscopy (SICM) (12), which utilizes the drop in ion current to image nonconducting surfaces, such as living cells, without making contact with the sample. With SICM it is today possible to image nm-sized features (13) and even resolve single protein complexes (14). In this work we use a modified SICM setup where it is possible to also apply an externally controlled hydrostatic pressure over the pipette (15). (For details on the experimental setup see SI Text.) Furthermore, as SICM is a scanning probe technique with potentially nanometer resolution in both the lateral and vertical directions it is possible to accurately position the pipette over a specific area of the lipid bilayer before the trap is turned on.

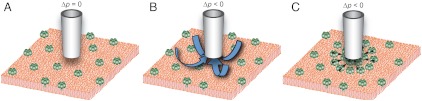
Fig. 1.

The principle of the hydrodynamic trap. (A) A conical pipette is lowered towards the SLB until it is approximately one tip radius above the lipid bilayer. (B) Negative hydrostatic pressure, Δp, is applied at the top of the pipette resulting in a flow of liquid into the pipette. (C) The resulting liquid flow acts on the protruding molecules in the SLB with a drag force causing them to accumulate, and become trapped, locally below the pipette.

After the pipette has been positioned above the lipid bilayer a hydrostatic pressure difference is applied between the top of the pipette and the surrounding solution. A negative pressure difference gives rise to a net flow of liquid into the pipette, as shown schematically in Fig. 1B. The liquid flow will exert a hydrodynamic force on the molecules in the SLB causing them to move in the direction of the liquid flow (16, 17). Molecules that protrude from the SLB will typically experience a higher hydrodynamic force than that felt by a lipid molecule in the SLB, and will therefore accumulate in the area beneath the pipette (see Fig. 1C). The size of the hydrodynamic trap corresponds approximately to the size of the tip aperture. This is due to the rapid decay of the hydrodynamic surface forces acting on the lipid bilayer when moving away from the pipette tip. It should also be noticed that as the molecules in the SLB are restricted to the lipid bilayer, the hydrodynamic trap only needs to be active in the plane of the SLB.

Theory.

The liquid flow into the pipette exerts a drag force on molecules in the underlying SLB. To estimate the magnitude of the hydrodynamic force on a single molecule, F_hydro(r), as a function of the radial distance r to the symmetry axis of the studied system, the following expression is used:

[1]

where α is a dimensionless function that depends on the geometry and surface coverage of molecular complexes in the SLB, R_c is the effective radius and h_c the height of the part of the studied molecular complex that is protruding above the SLB and σ_hydro(r) is the shear force per unit area on the surface given by:

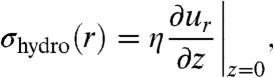[2]

where η is the viscosity of the liquid, u_r the radial flow velocity and z the distance to the surface. Note that it is not the shear force on the SLB itself which creates the hydrodynamic trap, but instead the liquid flow above the SLB which is proportional to σ_hydro. When deriving Eq. 1 it is, as a first approximation, assumed that the studied molecules at low surface coverage can be approximated as anchored spheres with a hydrodynamic force given by Stokes’ law. For this situation it can be shown that α = 1 (see SI Text for details). At higher surface coverage the different molecules start to shield each other and the hydrodynamic force per molecule decreases. For a densely packed layer of molecules only the upper part of the molecules are exposed to the liquid flow yielding α = R_c/3h_c (see SI Text). Because the hydrodynamic force given by Eq. 1 depends on the product R_ch_c, larger molecules will first be trapped, whereas smaller molecules experience a much weaker effect of the hydrodynamic trap. The anchor to the SLB can also affect how the protein molecules accumulate. However, for molecules bound to the SLB via a lipid anchor that is similar to the other lipids in the SLB, this effect will generally be relatively small.

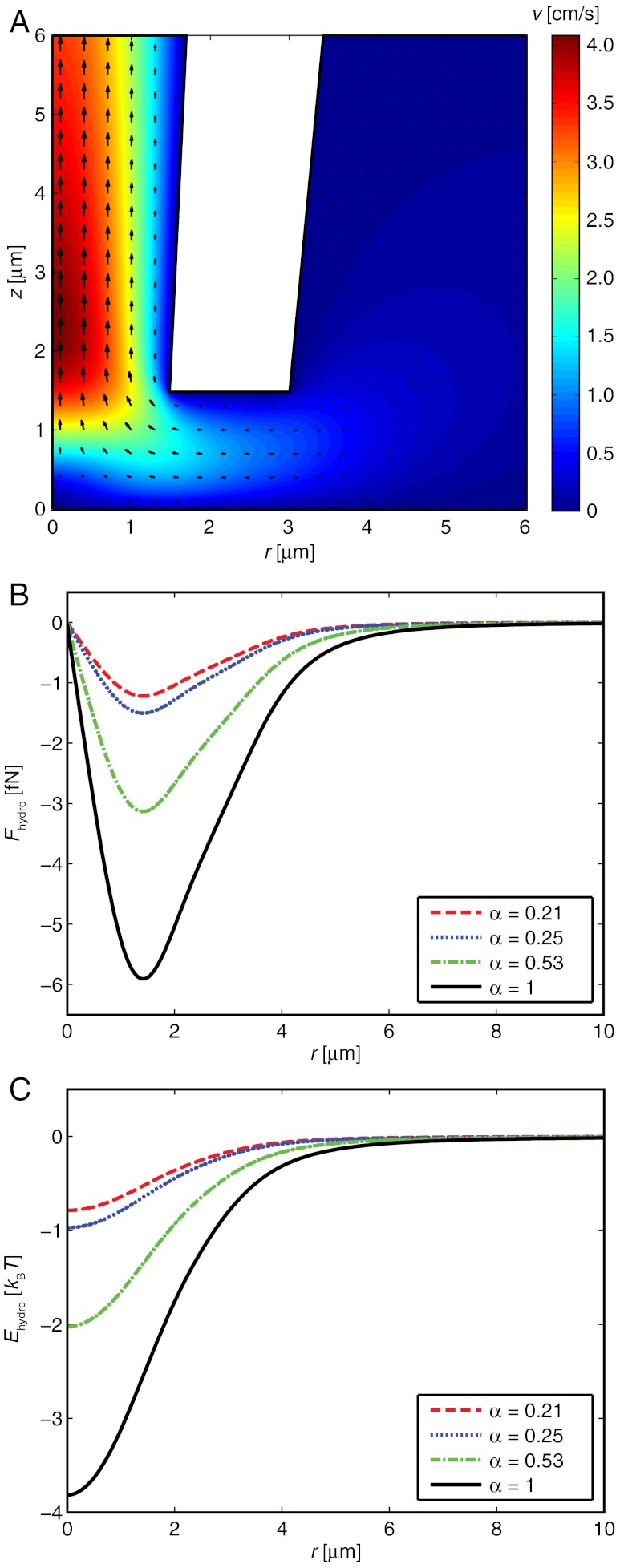
There exists no simple analytical expression that describes how σ_hydro(r) depends on parameters such as the applied pressure difference, the dimensions of the pipette, and the distance between the pipette tip and the SLB. However, finite element calculations can be used to accurately determine σ_hydro(r) for the case of creeping flow in an arbitrary flow enclosure. Here we use this to determine the hydrodynamic shear forces on the SLB. Fig. 2A shows the magnitude of the flow velocity, obtained from a finite element simulation, in and around a pipette with an inner tip radius of 1.5 μm and a half-cone angle of 2.7°, when a pressure of -1 kPa is applied at the top of the pipette. The pipette is placed one tip radius above the surface which has its center at r = 0. For a molecule with R_c = 3.1 nm and h_c = 5 nm, corresponding to the size of an anchored SA molecule (18) with R_c = (3V_SA/4π)^1/3, this gives the hydrodynamic forces shown in Fig. 2B.

Fig. 2.

Hydrodynamic forces and energies acting on a SA molecule in the SLB. (A) Finite element simulation of the flow velocity in a conical pipette for an applied pressure of -1 kPa. Arrows show the velocity components at different positions. (B) The hydrodynamic force on a single molecule with R_c = 3.1 nm and h_c = 5 nm due to the liquid flow in Fig. 2A. (C) The potential energy of the hydrodynamic trap experienced by the molecule in Fig. 2B.

The thermodynamic effect of the hydrodynamic forces on each type of molecule in the SLB can be described by a potential energy function, E_hydro(r), where E_hydro(r) is defined by the work required to bring a molecule along the membrane surface from infinity to a distance r from the center of the trap. Using Eq. 1 together with an analysis of variables of the parameters affecting σ_hydro(r) shows that E_hydro(r) can be written as:

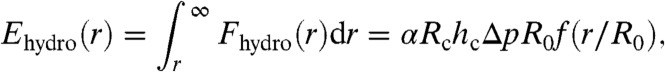[3]

where f is a function that depends on the relative radial distance r/R₀ along the surface, and is independent of the pressure drop over the pipette, Δp, the tip radius of the pipette, R₀, and the size of the studied molecules. Fig. 2C shows the potential energy of the trap due to the hydrodynamic force calculated in Fig. 2B. The full-width-half-maximum value of the trap in this case is equal to 2.5R₀. Note that the potential energy scales linearly with the applied pressure, thus for an applied pressure of -2 kPa the potential energy in Fig. 2C should be multiplied by a factor of two. Furthermore, if the tip aperture is reduced by a factor of ten, and thus also the width of the hydrodynamic trap, the pressure drop Δp must be increased by a factor of ten to maintain the magnitude of the potential energy of the trap.

When turning on the hydrodynamic trap, the mobile molecules start to migrate towards the center of the trap resulting in a change in surface concentration, c, of the studied molecules. To describe the effect the hydrodynamic forces have on the concentration profile the continuity equation in cylindrical coordinates in Eq. 4 is used (19):

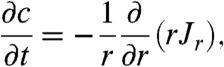[4]

where the radial molecular flux J_r is given by:

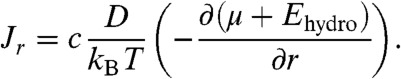[5]

Here D is the diffusivity of the studied molecules in the lipid bilayer, k_B the Boltzmann constant, T the absolute temperature and μ the chemical potential of the molecules. Stating how the chemical potential varies as a function of surface concentration is nontrivial, especially at higher surface coverage where intermolecular interactions are important. However, since the aim of this work is to illustrate the function of the hydrodynamic trap, and not to give a detailed description of the thermodynamics of interacting molecules in lipid bilayers, the following simplified description of the concentration dependence of the chemical potential is used:

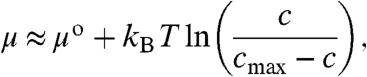[6]

where c_max is an effective parameter obtained by fitting the concentration profile to experimental data. The expression in Eq. 6 empirically describes the combined thermodynamic effects of entropy and all intermolecular forces in the studied system. Inserting the expression for μ in Eq. 6 into Eq. 5 results in:

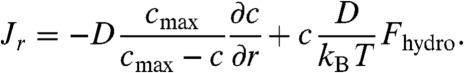[7]

At steady state, the solution to Eq. 4 with J_r given by Eq. 7 becomes:

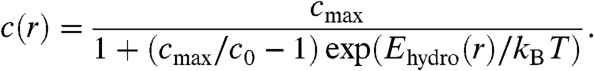[8]

Results and Discussion

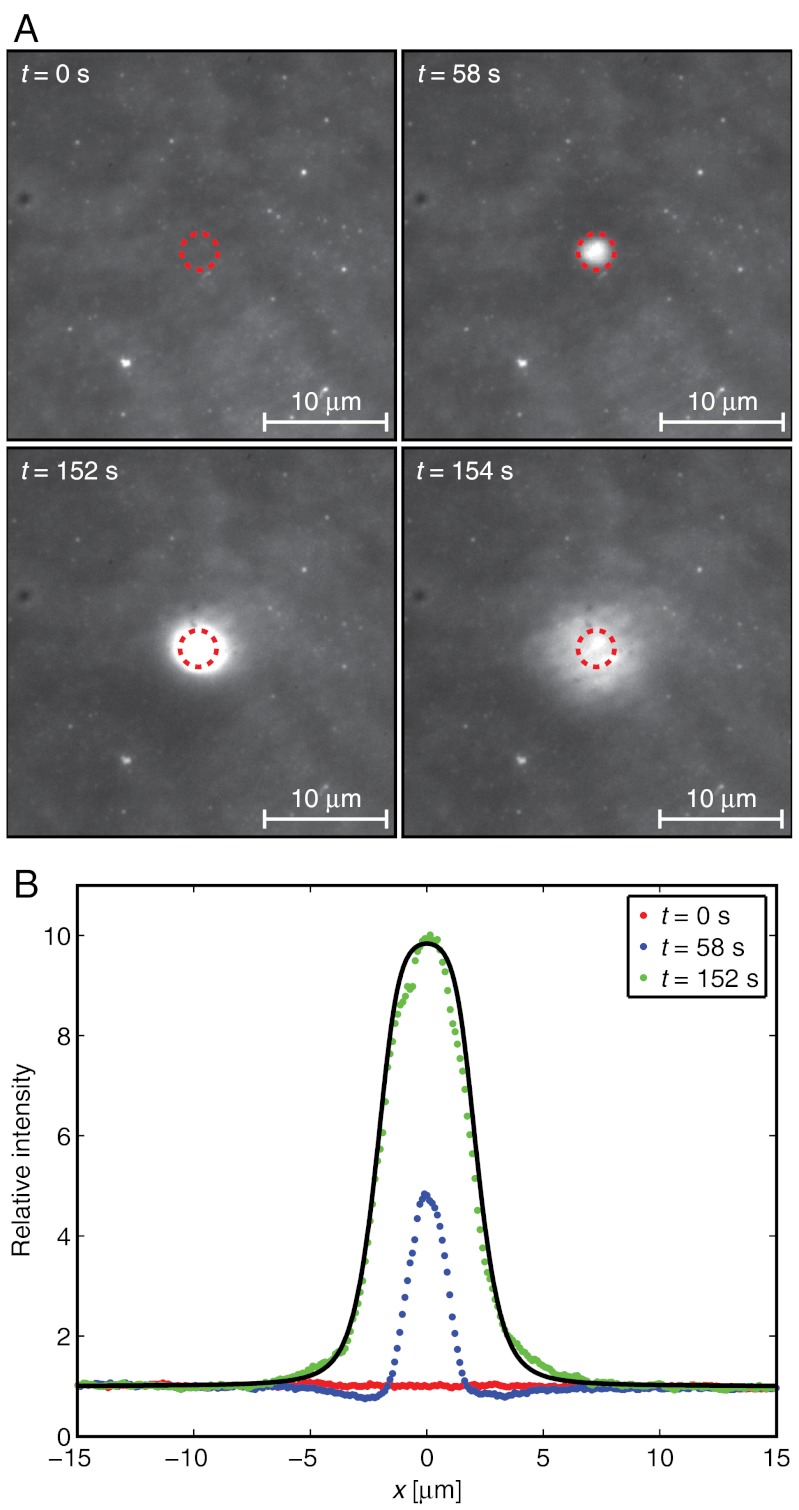
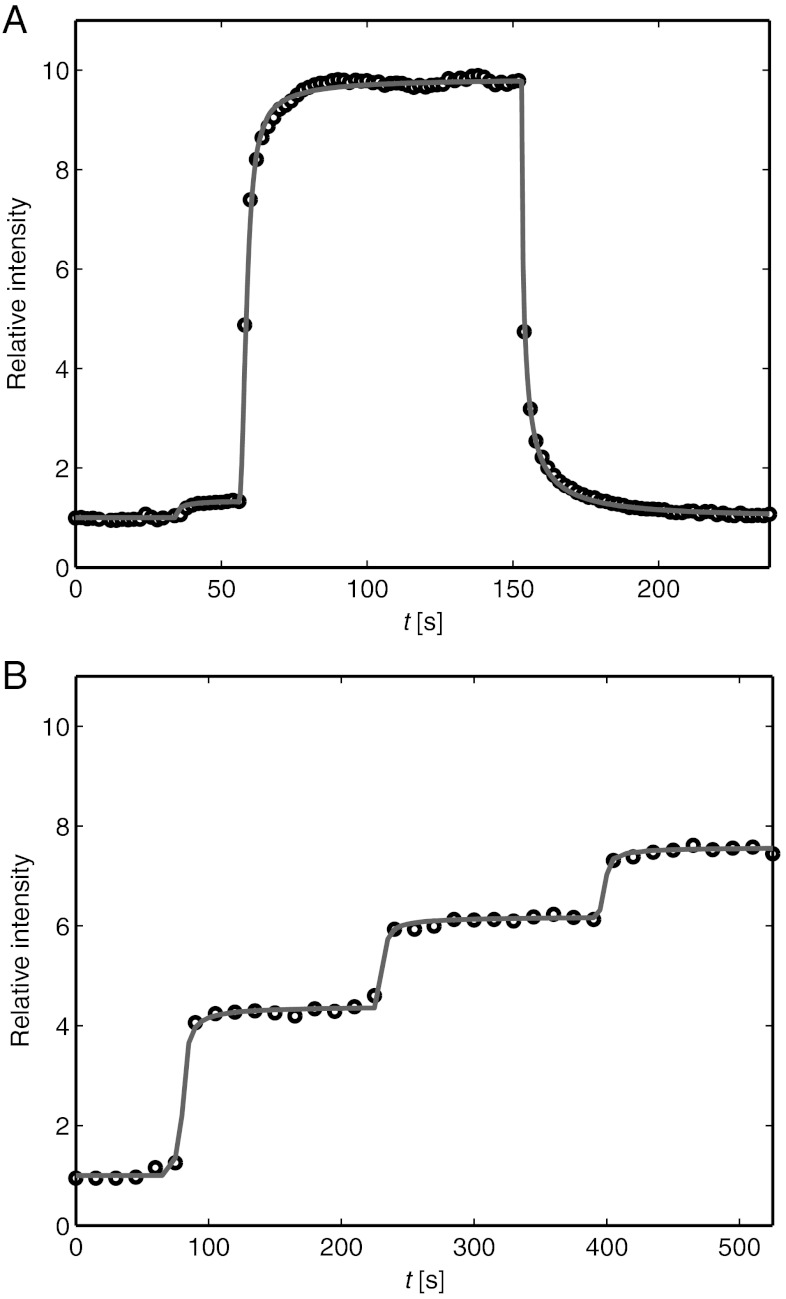
The properties of the hydrodynamic trap were characterized by trapping SA molecules bound to the upper monolayer of an SLB. Fig. 3 shows epifluorescence micrographs of the intensity from fluorescently labeled SA at different times before and after applying a hydrodynamic force to accumulate the proteins. Here, a pressure of -6 kPa is applied at the top of the pipette at t = 56 s and removed at t = 153 s. The initial surface coverage of proteins was in this case approximately 3%. Note that each pixel in the images contains several proteins, thus single proteins are not discernible. The size of the pipette and the distance between the pipette and the surface were the same as the parameters used in the simulations in Fig. 2. See also Movie S1, which shows the fluorescence intensity from SA when the hydrodynamic trap is turned on and off three subsequent times.

Fig. 3.

Trapping of fluorescently labeled SA. (A) Images showing the fluorescence intensity from SA bound to an SLB at different times. The hydrodynamic trap was turned on at t = 56 s and off at t = 153 s. Dashed circles correspond to the size of the tip aperture of the pipette. (B) Line profiles of the relative intensity through the center of the trap. The solid line is a fit to Eq. 8 of the data at t = 152 s.

As soon as the trap is turned on, the mobile SA molecules start to migrate towards the center of the trap. This results in a concentration increase of SA in the SLB beneath the pipette, whereas the concentration initially decreases just outside of the pipette (see the curve at t = 58 s in Fig. 3B). After a further approximately 30 s the concentration profile reaches steady state and does not change significantly until the trap is turned off. The solid line in Fig. 3B is a fit to the expression in Eq. 8 with c_max = 10.1 and E_hydro given by the α = 0.25 curve in Fig. 2C, multiplied by 6 to correspond to an applied pressure of -6 kPa. Note that the value of α is closer to 0.21 for densely packed molecules than to 1 for molecules spaced widely apart. Even though these values are just approximations, it is not unreasonable that α should be closer to the value of a densely packed layer of SA molecules, considering that the surface coverage of SA under the pipette is about 30% in this case. Fig. 4 shows line profiles of the steady-state surface coverage when a hydrostatic pressure of -6 kPa is applied at different starting concentrations of proteins on the surface.

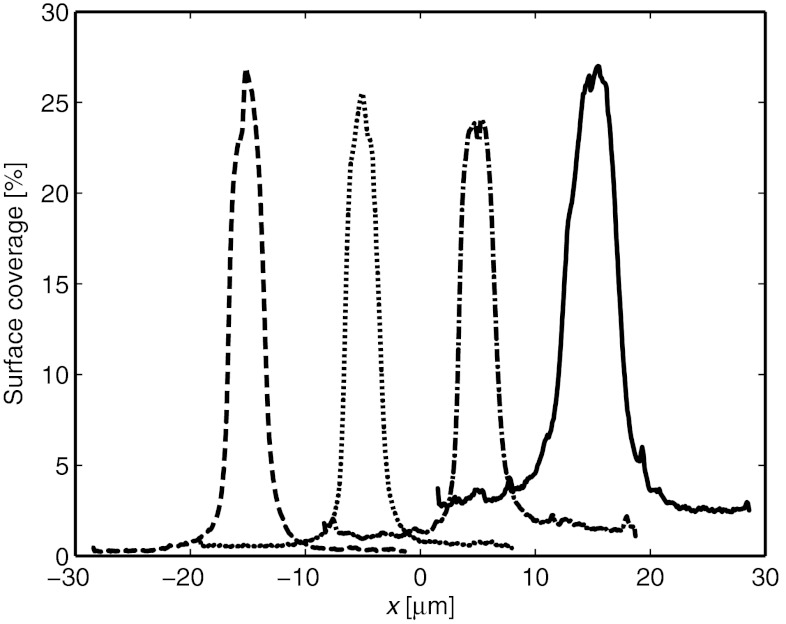
Fig. 4.

Line profiles showing the accumulation of SA at different starting concentrations. Before accumulation the surface coverage of SA was approximately (from left to right): 0.3%, 0.6%, 1.4% and 2.9%, respectively.

The line profiles shown in Fig. 4 are representative values of the surface coverage of SA obtained from different experiments. As the width of the trap is approximately given by the size of the tip aperture, pipettes with larger tip apertures will have broader line profiles. However, under the conditions in Fig. 4, the amplitude of the different line profiles was observed to be approximately independent of the size of the pipette used. Furthermore, the surface coverage at r = 0 reach a steady state value of 25–30%, independent of the average surface coverage of SA in the lipid bilayer. This can be compared to a surface coverage of approximately 70% for a SA crystal as determined by Darst, et al. (18). A surface coverage of 30% corresponds to each protein occupying a unit cell with a radius of about 5 nm, which is roughly 2 nm larger than the cross-sectional radius of a SA molecule. For the buffer solution used in the experiments the Debye length is of the order of approximately 1 nm. It is not unlikely that protein molecules spaced less than 2 Debye lengths apart act on each other with strong repulsive electrostatic forces, so that the effective radius of the protein molecules is increased. This could explain why the maximum surface coverage of SA in the trap is lower than that corresponding to close-packed SA molecules in a crystal.

When turning on the hydrodynamic trap the SA molecules immediately start to accumulate in the area beneath the pipette (see Fig. 5A). After a while the surface concentration reaches a stationary distribution with a fixed amplitude and width as seen in the curve at t = 152 s in Fig. 3B. The time it takes to reach equilibrium depends on the size of the hydrodynamic trap and the magnitude of the hydrodynamic force—a narrow trap combined with a large hydrodynamic force generally reaches steady state faster than a wide trap with a low hydrodynamic force. When turning off the trap protein molecules in the SLB start to diffuse out from the area beneath the pipette. The solid line in Fig. 5A shows the time dependence of the surface coverage at r = 0 obtained from finite element simulations. The value of the parameters c_max and α were 10.1 and 0.25, respectively, obtained from the fit of the experimental line profile at t = 152 s in Fig. 3C. E_hydro was multiplied with the applied pressure at the top of the pipette, which had been recorded at different times. The diffusivity of the protein molecules was determined to D = 1 μm²/s, obtained by fitting the relative intensity as a function of time after the hydrodynamic trap was turned off to simulated data with different values of D. No immobile fraction of SA molecules or formation of SA aggregates could be observed in the experiments. The obtained diffusivity is of the same magnitude as the diffusivity of SA in SLBs previously measured by fluorescence recovery after photobleaching (FRAP) in a lipid bilayer with a homogeneous surface coverage of SA molecules (17). However, compared to FRAP, we are measuring on accumulated and not on bleached molecules. This can, in principle, enable diffusion at different surface coverage to be studied. Furthermore, the contrast between the bleached and nonbleached region in FRAP is always in the interval 0 < I_bleach/I₀ < 1, whereas the interval in the hydrodynamic trap is roughly between 1 < I_trap/I₀ < c_max/c₀, where I₀ is the initial intensity, I_bleach the intensity after photobleaching and I_trap the intensity after turning on the trap. Thus, the fluorescence intensity in the trap can be more than c_max/c₀ higher than the intensity levels measured in FRAP, which is an advantage when studying the mobility of faint fluorescent molecules.

Fig. 5.

Kinetics of the hydrodynamic trap. (A) The relative intensity from SA at r = 0 vs time when a pressure of -6 kPa was applied at t = 56 s. At t = 153 s the pipette is moved away from the surface and the pressure is turned off. (B) The relative intensity at different applied pressures (from left to right): 0 kPa, -0.6 kPa, -1.1 kPa and -2.0 kPa, respectively. The solid lines correspond to values from finite element simulations.

Fig. 5B shows the accumulation of SA beneath the tip of a pipette at different applied pressures. With the parameter c_max = 10.1, the same as in Fig. 5A, the different steps in Fig. 5B had values of: α = 0.55 (0 to -0.6 kPa), α = 0.40 (-0.6 to -1.1 kPa) and α = 0.28 (-1.1 to -2.0 kPa). This can be compared to the value α = 0.25 obtained for the accumulation at high surface coverage shown in Fig. 5A. Even though the absolute value of α may vary somewhat between experiments the general trend is that α decreases with increasing surface coverage. An explanation of this behavior could be that the protein molecules are progressively more shielded by each other at higher surface coverage which has the effect of reducing α (see also the discussion in connection with Eq. 1). However, the surface coverage at r = 0 after the different steps were 11%, 16% and 19%, respectively, which are not drastically different. An additional explanation to the decrease in α, and thus also the decrease in the potential energy of the trap, could be increasing intermolecular repulsion between the different protein molecules at higher surface coverage. Thus, the accumulation of molecules protruding from a lipid bilayer can provide insights into both the local mobility and the intermolecular forces acting between these molecules. However, more refined theoretical models, than those used in this work, are needed in order to fully understand and quantify the intermolecular interactions existing at higher surface coverage.

Experiments were also conducted on an SLB containing 1 wt% of the fluorescently labeled lipid Oregon Green® 488 1,2-dihexadecanoyl-sn-glycero-3-phosphoethanolamine (OG-DHPE), which has a fluorescent group added to the head of the lipid. Compared to the accumulation of SA at low pressures the accumulation of OG-DHPE was about 70 times lower (8–30% intensity increase at r = 0 for pressures ranging between -5 to -20 kPa). Inserted into Eq. 8 this results in α ≈ 0.5, where R_c = 0.5 nm and h_c = 0.5 nm have been used as estimates of the cross sectional radius and height of the protruding part of the OG-DHPE molecule and where it is assumed that c_max≫c. This value of α is of the same magnitude as the value obtained in the SA experiments. Since the anchor to the SLB is of comparable size for both SA, which is anchored via a biotinylated lipid, and OG-DHPE, this indicates that it is the protruding part of the molecules that dominates the extent of accumulation in this case.

In addition to the examples already discussed in this work, it is also possible to move molecules to different positions of the SLB by moving the pipette laterally using the piezoelectric positioning stage (see Movie S2). This could be used to study kinetic reactions between two types of molecules in an SLB, by moving one type of molecule from an area in the lipid bilayer to an area with the second type of molecule to start the reaction. Another possible application of the hydrodynamic trap is to study the accumulation of a population of different types of molecules, or molecules with different number of anchors to the SLB, and observe how the molecules distribute and behave in the trap. This type of experiment would yield information on molecular interactions between different types of molecules in the SLB and could be used to study multivalent binding and association.

Another intriguing application would be the use of the hydrodynamic trap to capture and manipulate molecules in the plasma membrane that surrounds a living cell. This could potentially be used to obtain fundamental information about how molecules interact and organize in the membrane of living cells. However, there are a number of differences between the membrane of a living cell and an SLB which needs to be overcome before this is possible. One is that the SLB is supported by a rigid and planar surface whereas the plasma membrane of a cell is generally curved and can deform due to the liquid flow through the pipette. Another complication with cells compared to SLBs is that larger complexes protruding from the plasma membrane can shield the hydrodynamic flow from smaller molecules closer to the surface, thus reducing the strength of the trap.

In summary, we have presented a noncontact method to move and trap protein molecules that protrude from a lipid bilayer. In addition of increasing the local concentration of molecules in the SLB the technique could also yield information about the interaction and organization/size of different molecules in the SLB. This type of information is often nontrivial to obtain experimentally and the hydrodynamic trap could therefore find interesting use in various bioanalytical applications where SLBs are used to study the function and interaction between different membrane-associated molecules.

Material and Methods

Supported Lipid Bilayers.

An SLB was formed on a clean glass slide, glued to the bottom of a petri dish with a 3 mm hole, by adsorption and subsequent rupture of lipid vesicles. The vesicles consisted of 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC) with either 0 or 0.1 wt% of 1,2-dipalmitoyl-sn-glycero-3-phosphoethanolamine-N-(cap biotinyl) (biotin-PE). POPC vesicles containing 1 wt% Oregon Green® 488 1,2-dihexadecanoyl-sn-glycero-3-phosphoethanolamine (OG-DHPE) were also used for some of the experiments in this work. Having a x∶y mixture of 0 and 0.1 wt% biotin-PE vesicles was found to approximately result in an SLB containing 0.1 × y/(x + y) biotin-PE, which was used to make SLBs with different surface coverage of biotin-PE (see SI Text). The buffer solution used in the experiments was a mixture of 125 mM NaCl, 10 mM tris[hydroxymethyl]aminomethane and 1 mM ethylenediaminetetraacetic acid disodium salt dihydrate, adjusted to a pH of 7.4. After the formation of an SLB from the lipid vesicle suspension the vesicle solution was first replaced with buffer solution and then with a solution containing 10 μg/ml (approximately 170 nM) of the protein SA. The SA molecules were labeled with the fluorescent group Oregon Green® 488, and were allowed to bind to biotin-PE in the SLB for 30 min after which the binding of proteins had reached equilibrium. To estimate the surface coverage, Γ, of SA it was assumed that all biotin-PE receptors in the upper monolayer of the SLB bind a single protein. By further assuming that biotin-PE distributes equally between both monolayers of the SLB this gives a surface concentration of Γ(0.1 wt%) = 1.15 × 10^-3 proteins/nm². With a cross-sectional area of a SA molecule of 25 nm² (18), this corresponds to a surface coverage of 2.84%.

Experimental Setup.

The intensity from SA in the SLB was studied with an inverted Nikon Eclipse TE200 microscope with a custom-made holder for the conical pipette. This holder was mounted on a piezoelectric three-dimensional positioning system that allowed for sub-100 nm movements of the pipette in the x-, y-, and z-direction. The conical glass pipettes were pulled from borosilicate glass capillaries with an inner diameter of 0.5 mm and an outer diameter of 1.0 mm. This was made with a laser-based pipette puller resulting in pipettes with an approximate tip radius of 1–1.5 μm and a half-cone angle of 3–4° (see Fig. S1). To bring the pipette to within one tip radius of the surface the ion current between an Ag/AgCl electrode in the pipette and an Ag/AgCl reference electrode in the bath outside the pipette was measured. The pipette was brought closer to the surface with the piezoelectric positioning system until the current to the oscilloscope had dropped by typically 1–2%, roughly corresponding to the pipette being one tip radius above the surface.

Hydrostatic pressure was applied to the top of the pipette using a stepper motor controlling the position of a 10 ml syringe. The pressure was monitored by a custom-made pressure sensor which used feedback to control the position of the stepper motor via a custom-written LabVIEW 2009 program. For the accumulation experiments hydrostatic pressures between -0.5 to -20 kPa was applied at the top of the pipette after which the fluorescence intensity from SA at different positions of the lipid bilayer was studied.

Simulations.

Numerical simulations were made using COMSOL Multiphysics 4.2, a program that solves partial differential equations using the finite element method. The simulations were made in cylindrical coordinates for the geometry shown in Fig. S2, with an inner half-cone angle θ = 2.7°, an inner tip radius R₀ = 1.5 μm and an outer tip radius R₁ = 3.0 μm, unless otherwise stated. These parameters were chosen based on an image of the pipette tip taken with optical microscopy (see Fig. S1). For the data in Fig. 5B: θ = 3.5°, R₀ = 1.1 μm and R₁ = 2.2 μm. Three different types of simulations were performed: (i) simulation of the ion current in the pipette, (ii) simulation of the flow velocity due to a pressure difference over the pipette and (iii) a time-dependent simulation of the concentration of SA in the lipid bilayer due to the hydrodynamic forces.

To simulate the ion current the stationary Electrostatics module was used in cylindrical coordinates (for boundary conditions see SI Text). The total ion current through the pipette at different distances, h, between the pipette and the surface were calculated, yielding the electrical resistance over the pipette versus h. This was used to determine the distance between the pipette and the surface from the change in ion current measured in the experiments. For the pipette with θ = 2.7°, R₀ = 1.5 μm and R₁ = 3.0 μm the current dropped by 1.3% when the distance to the surface was changed from 10R₀ to R₀. For the situation in Fig. 5B the drop in ion current was 3.4%, which corresponds to a distance of h = 0.56R₀.

The simulations of the liquid flow into the pipette were made by solving Navier-Stokes equations for an incompressible flow using the time-independent Creeping flow module in cylindrical coordinates (for boundary conditions see SI Text). The flow was in all cases solved for a pressure drop of -1 kPa over the entire pipette. From this data the hydrodynamic shear force, σ_hydro(r), was determined as a function of the radial distance, r, along the underlying surface.

To simulate the concentration of proteins at different positions in the hydrodynamic trap, as a function of time after the trap had been turned on or off, the time-dependent PDE module in one dimension was used. Here Eq. 4 was solved with the molecular flux given by Eq. 7. The value of σ_hydro(r) was imported from the simulations of the flow velocity in the pipette, and it was assumed that R_c = 3.1 nm and h_c = 5 nm. The parameters c_max and α were determined by fitting a line profile of the relative intensity of SA, at steady state, to the analytical expression in Eq. 8. The diffusivity of the proteins were then determined by fitting the decrease in intensity at r = 0 as a function of time when the trap had been turned off.

More detailed information about the experimental setup and procedure, the analysis of the data and the simulations are given in the SI Text.