Abstract
We investigated the development of dual-retrieval processes with a low-burden paradigm that is suitable for research with children and neurocognitively impaired populations (e.g., older adults with mild cognitive impairment or dementia). Rich quantitative information can be obtained about recollection, reconstruction, and familiarity judgment by defining a Markov model over simple recall tasks like those that are used in clinical neuropsychology batteries. The model measures these processes separately for learning, forgetting, and reminiscence. We implemented this procedure in some developmental experiments, whose aims were (a) to measure age changes in recollective and nonrecollective retrieval during learning, forgetting, and reminiscence and (b) to measure age changes in content dimensions (e.g., taxonomic relatedness) that affect the two forms of retrieval. The model provided excellent fits in all three domains. Concerning (a), recollection, reconstruction, and familiarity judgment all improved during the child-to-adolescent age range in the learning domain, whereas only recollection improved in the forgetting domain, and the processes were age-invariant in the reminiscence domain. Concerning (b), although some elements of the adult pattern of taxonomic relatedness effects were detected by early adolescence, the adult pattern differs qualitatively from corresponding patterns in children and adolescents.
Keywords: recollection, reconstruction, familiarity, forgetting, reminiscence, Markov models
Strong (1913) is often credited with being the first to provide evidence that episodic memories are sometimes accompanied by mental reinstatement of realistic details of prior experience (recollective retrieval) and sometimes are not (nonrecollective retrieval). The traditional line of attack on measuring the two forms of retrieval relies, as Strong did, on item recognition as the focal memory task. Subjects make old/new decisions about items in the usual way, and their decisions are supplemented with metacognitive judgments that are thought to identify which form of retrieval was responsible for individual decisions. This, too, is in the spirit of Strong’s work, which relied on the introspective reports that were common in his era. Nowadays, the most frequently used techniques are remember/know judgments (Tulving, 1985), inclusion/exclusion judgments, from which the recollective and nonrecollective parameters of the process dissociation model are estimated (Jacoby, 1991), and confidence judgments, which allows recollective and nonrecollective parameters to be extracted from the receiver operating characteristic (ROC; Yonelinas, 1994).
This general approach has been the subject of lively controversy, owing to a pair of validity challenges. One challenge is that the dual-retrieval distinction is simply unnecessary because models with a single nonrecollective process (usually called familiarity), especially the unequal variance signal-detection model (Glanzer, Kim, Hilford, & Adams, 1999; Lockhart & Murdock, 1970), are adequate to handle item recognition. A second challenge is that even if recognition involves dual-retrieval operations, supplementary judgments such as remember/know, inclusion/exclusion, and confidence are invalid methods of diagnosing them. Examples of this argument have appeared in the literature in connection with each of the three procedures (Donaldson, 1996; Dunn, 2004, 2008; Ratcliff, Van Zandt, & McKoon; 1995; Rotello, Macmillan, & Reeder; Wixted, 2007). In an integrative review of such work, Malmberg (2008) concluded that all of the procedures are invalid because accumulated data show that item recognition is controlled by a single familiarity process.
How, then, are dual-retrieval processes are to be measured? Two general solutions have been suggested. One is to preserve recognition as the focal memory task and institute methodological refinements that respond to the challenges to current procedures. For example, Malmberg (2008) proposed that item recognition could be replaced by forms of recognition that cannot be reduced to a single familiarity process, such as associative recognition and plurality discrimination (see Yonelinas, 2002). Also, Ingram, Mickes, and Wixted (in press) proposed that item recognition can still be used if further layers of metacognitive judgment are added to existing procedures in order to obtain better separation between the two retrieval processes. The second solution is to switch to recall as the focal memory task (Brainerd, Reyna, & Howe, 2009; Brainerd & Reyna, 2010). Debates over whether performance is controlled by a single retrieval process evaporate because it has long been known that recall involves two distinct processes (Bower & Theios, 1964; Kintsch & Morris, 1965; Greeno, 1968; Greeno, James, & DaPolito, 1971; Waugh & Smith, 1962), and well-developed mathematical models, in the form of two-stage Markov chains, exist for separating and quantifying those processes (for reviews, see Brainerd, Howe, & Desrochers, 1982; Greeno, 1974). The recall solution, simply put, is to measure recollective and nonrecollective retrieval by identifying each with one of the Markov stages (Brainerd et al., 2009), which means that challenges to the diagnostic power of metacognitive judgments do not arise because measurements of these processes fall directly out of conventional recall data
In this article, we report some experiments that implemented the recall solution in order to investigate two topics that are fundamental to our understanding of recollective and nonrecollective retrieval but on which surprisingly little evidence is available. One is the contrasting theoretical proposals that have been advanced about the early developmental course of the two forms of retrieval. The other topic is how, once initial learning is complete, recollective and nonrecollective retrieval change as time passes—more specifically, how they contribute to normal forgetting and to test-induced reminiscence. Both topics are introduced in the next section. They are preceded by an overview of the dual-retrieval conception of recall, its associated measurement model, and prior findings.
Overview of the Research
Dual-Retrieval Processes in Recall
In this conception, items are recalled via a recollective operation, which is called direct access, and via a nonrecollective one, which is called reconstruction. Reconstruction is accompanied by a slave judgment operation that evaluates the familiarity of reconstructed items. The recollective operation accesses verbatim traces of items’ prior presentations directly, without searching through traces of other items, and for that reason, it is the faster of the two. Direct access is also the more accurate operation because it supports errorless recall: When an item is retrieved in this way, its surface form is symbolically reinstated, along with associated contextual details, so that the item can simply be read out of consciousness as it is seen in the mind’s eye or heard in the mind’s ear. Because recollective phenomenology is traditionally defined as reinstatement of vivid, realistic details, this is why direct access is the recollective operation.
Although direct access is fast and highly accurate, it must be augmented by reconstructive retrieval, for two reasons. The first is that during initial learning, direct access rapidly degrades as a recall test proceeds, the reason being that the types of traces that it accesses are quite sensitive to proactive and concurrent interference (Barnhardt, Choi, Gerkens, & Smith, 2006; Brainerd & Reyna, 1993; Payne, Elie, Blackwell, & Neuschatz, 1996). Owing to interference sensitivity, verbatim traces are unstable and tend not to remain accessible from trial to trial. Exclusive reliance on direct access is only possible if sufficient learning trials are provided so that the verbatim traces that are stored are stable enough to survive from trial to trial—something that is rarely done in recall experiments, which typically involve only a single learning trial.
The nonrecollective operation, reconstruction, avoids this problem by regenerating items from stable episodic traces of partial-identifying information, particularly traces of semantic information (e.g., “soft drink” and “cola” for Coke). Here, it is well known—for instance, from the tip-of-the-tongue and feeling-of- knowing literatures—that subjects can access a variety of partial-identifying information about items in advance of recalling the items themselves (e.g., Brown & McNeill, 1966; Hicks & Marsh, 2002; Koriat, 1993, 1995; Kurilla & Westerman, 2010; Schacter & Worling, 1985). Examples include the semantic features in Osgood’s (1952) model of meaning (Koriat, Levy-Sadot, Edry, & Marcas, 2003). Reconstruction searches memory for items that match such features, generating sets of candidate items (e.g., Coke, Pepsi, RC, Jolt) that are small enough to be processed within the time constraints of a recall test. Because the features that are used to construct such sets do not uniquely identify specific items as targets, the sets will normally contain nontargets (Pepsi, RC, Jolt), too. To avoid high levels of intrusions, a judgment operation performs confidence checks on reconstructed items before they are passed on for output. This is where the familiarity operation of dual-process models of recognition enters the recall model.
It is assumed that a reconstructed item, like an item probe on a recognition test, generates a familiarity signal that is processed by the judgment operation. As in signal detection models, it is assumed that the judgment operation processes the familiarity signals of reconstructed items by setting a decision criterion and only allowing the ones that exceed the criterion to be recalled. Thus, the key difference between nonrecollective retrieval in recognition versus recall is that it involves a single operation in recognition (familiarity judgment) and pair of operations in recall (reconstruction + familiarity judgment). Brainerd et al. (2009) noted that the obvious resemblance between the latter idea and classic generate/recognize models of recall (e.g., Anderson & Bower, 1972; Kintsch & Morris, 1965) might be thought to imply that the dual-retrieval conception of recall is susceptible to the well-known recognition failure criticism of generate/recognize models (i.e., that subjects sometimes recall words that cannot be recognized; Tulving & Thomson, 1973). They showed, however, that this criticism is not applicable because the direct access operation handles the recognition failure phenomenon.
Although nonrecollective retrieval has the advantage, relative to recollective retrieval, that it processes stable memory representations, its disadvantage is that it is error prone. Like the familiarity operation in recognition, which sometimes produces false alarms to distractors, the corresponding operation in recall sometimes allows nontargets to be output. Thus, the advantage of recollective retrieval (high accuracy) is the disadvantage of nonrecollective retrieval, the advantage of nonrecollective retrieval (stable traces) is the disadvantage of recollective retrieval, and together, the two forms of retrieval compensate for each other’s weaknesses to maximize recall.
Recollective and nonrecollective retrieval are measured by fitting two-stage Markov chains to recall data. Extensive prior research with such models has shown that they deliver good fits throughout the life span (for a review, see Brainerd et al., 2009). These models represent the process of learning to recall list items over study-test trials as consisting of three discrete performance states, through which items pass as trials accumulate: an initial no-recall state U, in which the probability of successful recall is zero; an intermediate partial-recall state P, in which the probability of successful recall has some average value 0 < p < 1; and a terminal perfect-recall state L, in which the probability of successful recall is 1. Items are assumed to be in state U before the initial study cycle. After the first trial, or after any subsequent trial, an item that was in U may have transitioned to P, transitioned to L, or remained in U. Items that transition to L remain there on all subsequent trials (i.e., L is an absorbing state), items that transition to P can transition to L on some subsequent trial, and items that remain in U can transition to P or L on some subsequent trial.1 As these models are Markovian, inter-state transitions are all-or-none, so that the probability of correct recall does not increase smoothly from 0 to 1. Instead, at the level of Subjects X Conditions X Items, the correct recall probability has only three values (0, p, 1), with discrete transitions between values. It might be thought that this somehow implies that inter-trial improvements in recollective and nonrecollective retrieval must involve all-or-none transitions from unsuccessful to successful retrieval. It does not imply that. In a two-stage Markov chain, all-or-none transitions occur at the level of response probability, not at the level of improvements in retrieval processes. As Restle (1965) explained long ago, all-or-none transitions in response probability do not imply all-or-none transitions in underlying memory processes, and on the contrary, continuous changes in such processes can produce all-or-none transitions at the level of performance when the output scale involves a threshold mechanism.
Recollective retrieval is mapped with state L, while nonrecollective retrieval is mapped with state P. Recollective retrieval is measured via model parameters (direct access parameters) that give the probability of transitioning to L from P or U. With respect to nonrecollective retrieval, the reconstruction operation is measured via model parameters that give the probability of transitioning to state P from state U, whereas familiarity judgment is measured by parameters that give the probability of successful recall of items that are in state P. This method of measurement illustrates a point that was mentioned earlier—namely, that in order to measure dual-retrieval processes, the data of conventional recall tasks (e.g., associative, free, cued) do not have to be enriched with metacognitive judgments. Beyond this, Brainerd et al. (2009) showed that the difficulty of such tasks can be adjusted somewhat to take account of the cognitive limitations of different subject populations. It was shown that in the limit, the outcome spaces of experiments in which subjects participate in only three study-test trials per list are adequate to define a two-stage Markov model that contains two direct access parameters, two reconstruction parameters, and two familiarity judgment parameters.
This model is fully described in the Appendix (Equations A1–A11), and the retrieval processes that it measures are summarized in Table 1. There, it can be seen that there is a set of three parameters (D1, R1, and J1) that measure direct access, reconstruction, and familiarity judgment on Trial 1, and a second set (D2, R2, and J2) that measures these processes on Trials 2 and 3. As can be seen in the Appendix, the model recovers estimates of all of these parameters and conducts fit tests by simultaneously solving Equations A2–A9 for recall data consisting of three-trial sequences of errors and successes. The very low-burden tasks over which this model is defined allow dual-retrieval processes to be measured reliably in children, in adults with psychotic conditions (e.g., schizophrenia; see Brainerd et al., 2009, for illustrative data), and in adults with neurocognitive impairments (e.g., Alzheimer’s dementia; see Brainerd et al., 2009, for illustrative data).
Table 1.
Retrieval Processes that are Measured by the Markov Chain with Repeated Recall Data and Long-Term Retention Data
| Process/parameter | Definition |
|---|---|
| Recollective retrieval | |
|
| |
| D1 | The probability that a verbatim trace of an item’s presentation on a study list can be accessed after the first study cycle |
| D2 | For any item whose verbatim trace could not be accessed following prior study cycles, the probability that such a trace can be accessed after the current study cycle |
|
| |
| Nonrecollective retrieval | |
|
| |
| Reconstruction: | |
| R1 | For any item for whose verbatim trace cannot be accessed after the first study cycle, the probability that it can be reconstructed after that study cycle |
| R2 | For any item for whose verbatim trace cannot be accessed after the current study cycle and that could not be reconstructed after prior study cycles, the probability that it can be reconstructed after the current study cycle |
| Familiarity judgment: | |
| J1 | For any item that is reconstructed following the first study cycle, the probability that the reconstruction is judged to be familiar enough to output |
| J2 | For any item that is reconstructed following any study cycle after the first one, the probability that the reconstruction is judged to be familiar enough to output |
The mapping of recollective and nonrecollective retrieval with states L and P, respectively, of two-stage Markov chains is a theoretical one in the sense that under their definitions, reconstruction should be error prone but direct access should not be. There is empirical support for this mapping, in the form of parameter validity results—experimental findings in which (a) manipulations that embody the process definition of direct access selectively affect parameters that measure the difficulty of transitioning to L from U or P and (b) manipulations that embody the process definition of reconstruction selectively affect parameters that measure the difficulty of transitioning to P from U. Various parameter validity findings were reviewed by Brainerd et al. (2009). Concerning a, two prominent examples of manipulations from the recognition literature that have long been treated as ones that should selectively affect recollective retrieval are list length and studying lists of cue-target word pairs versus lists of single target words (see Yonelinas, 2002). Likewise, in recall experiments with the dual-retrieval model, shorter lists and lists that supply a distinct cue for each target have been found to elevate direct access parameters but not reconstruction parameters (Brainerd & Reyna, 2010; Brainerd et al., 2009). Concerning b, adding semantic structure to word lists is an obvious example of a class of manipulations that ought to make reconstruction (but not direct access) easier by providing salient semantic features that can be processed to construct sets of candidate items. Consistent with that hypothesis, Brainerd and Reyna (2010) found that adding taxonomic relations to word lists increased reconstruction parameters but not direct access parameters, and Gomes, Stein, and Brainerd (2011) found that adding valence relations had the same effect.
Development of Dual-Retrieval Processes
One set of theoretical questions that was investigated in the experiments that we report dealt with the early developmental course of recollective and nonrecollective retrieval. A known consequence of the use of supplementary metacognitive tasks to measure dual-retrieval processes is that it has largely precluded experimentation on such questions. Theoretical hypotheses about the mechanisms that underlie recollective and nonrecollective retrieval (e.g., Yonelinas, 2002), as well as hypotheses about the brain regions that support them (e.g., Ranganath, 2010), have led to contrasting proposals about their ontogenesis (Brainerd et al. 2009). For instance, based on traditional ideas from the recognition literature, Ghetti and associates (e.g., Ghetti, 2008; Ghetti & Angelini, 2008) proposed that the development of nonrecollective retrieval is largely complete by the end of the preschool years, so that the improvements in episodic memory that occur during childhood and adolescence are due to the growth of recollective retrieval. In contrast, based on other theoretical ideas, other investigators have proposed that such improvements are due to the growth of nonrecollective as well as recollective retrieval, that both forms of retrieval continue to develop through young adulthood, and that they contribute differentially to age improvements during different age ranges and in memory for different types of material (Brainerd et al., 2009).
The fact that metacognitive judgments are high-burden methodologies that require subjects to comprehend instructions about how to introspect on phenomenological qualities of their memories and to perform those introspections reliably has meant that contrasting hypotheses about development have gone largely untested (Brainerd et al., 2009). Of the three methodologies mentioned earlier, remember/know is the only one that has been used in developmental studies. However, only two such studies have been published (Billingsley, Smith, & McAndrews, 2002; Ghetti & Angelini, 2008), owing to a pair of validity problems: Adult remember/know instructions must be simplified for children, so that comparing the data of different age levels is hazardous because different methodologies are used (Brainerd et al., 2009), and even with simplified instructions, children’s understanding of the instructions is different than adults’ (Ghetti, 2008). In addition to precluding developmental studies, the high-burden nature of metacognitive tasks means that they exceed the capabilities of other populations that are of theoretical interest to memory researchers. A prominent example is older adult populations with neurocognitive impairments, such as Alzheimer’s dementia, Parkinson’s dementia, or vascular dementia. The relative contributions of recollective and nonrecollective retrieval to the characteristic memory deficits of these conditions is a matter of considerable significance, and in the specific case of Alzheimer’s dementia, a common hypothesis is that transitions to this condition are characterized by almost complete loss of recollective retrieval, coupled with sparing of familiarity (for a review, see Bugaiska, Morson, Moulin, & Souchay, 2011).
Although metacognitive judgments are problematical for children and older adults with neurocognitive impairments, conventional recall tasks are well within their capabilities. In that connection, there is a large literature on the development of associative, free, and cued recall from the preschool years onward (for a review, see Schneider & Pressley, 1997). Likewise, there is a large literature on these same tasks in impaired adults. Indeed, recall tests figure centrally in neuropsychological batteries that are used to diagnose impairment (e.g., Langa et al., 2005) because such tests can be performed by demented adults as well as by healthy adults and adults with milder forms of impairment. Commonly used examples of these clinical recall instruments are the Consortium to Establish a Registry for Alzheimer’s Disease (CERAD; Morris et al., 1989) recall test, which involves three study-test trials on a short word list, and the Rey Auditory Verbal Learning Test (RAVLT; Rey, 1941), which involves five study-test trials on a short word list. Moreover, although neuropsychological batteries contain other types of tests (e.g., for language, for executive function), recall performance is the best single correlate of impairment diagnoses (Petersen et al., 1999).
In the experiments that are reported in this article, we exploited the low-burden feature of the recall approach to generate some evidence on contrasting developmental predictions about recollective and nonrecollective retrieval. Here, our overriding concern was to pit the hypothesis that developmental improvements in recall are exclusively due to the growth of recollective retrieval against the hypothesis that they are due to the growth of both recollective and nonrecollective retrieval. A second concern was to exemplify how the separation of developmental trends in recollective retrieval from developmental trends in nonrecollective retrieval can supply process explanations of age variation in the effects of important content variables. Here, we studied two familiar content manipulations, taxonomic relatedness of list items and typicality of list items. The effects of both manipulations on the accuracy of recall are known to vary dramatically between childhood and adolescence (for reviews, see Bjorklund, 2004; Bjorklund & Muir, 1988). In adults, taxonomic relatedness impairs associative recall (e.g., Underwood, Ekstrand, & Keppel, 1965) but facilitates free recall (e.g., Mandler, 1967); both effects being larger for typical than for atypical exemplars of categories. Recent research with dual-retrieval models (Brainerd & Reyna, 2010) revealed that the effects of taxonomic relatedness on underlying retrieval operations in the two paradigms are qualitatively similar—with categorized items impairing recollection but facilitating reconstruction and familiarity judgment, relative to unrelated items. This research showed, further, that the reason that the net effect of taxonomic relatedness is negative in associative recall but positive in free recall is that free recall is much more dependent on nonrecollective retrieval. The effects of taxonomic relatedness emerge gradually during childhood and adolescence, and although these changes have been extensively studied in free recall (Bjorklund, 1987), little is known about corresponding changes in associative recall (Brainerd, Reyna, Howe, & Kingma, 1990). Thus, we focused on child-to-adolescent changes in how taxonomic relatedness and exemplar typicality affect associative recall. We were especially interested in (a) the emergence during this age span of the standard adult pattern (i.e., taxonomic relatedness impairs associative recall on both the cue and target sides of word pairs; Underwood et al., 1965) and (b) whether this is due to developmental changes in how taxonomic relatedness affects recollective or nonrecollective retrieval. It is conceivable that some of these effects are qualitatively different in children versus adults.
Dual-Retrieval Operations in Forgetting and Reminiscence
Another major objective of our experiments was to extend the recall approach from initial learning of dual-retrieval operations to their subsequent forgetting and reminiscence (test-induced recovery following a forgetting interval). Considering the prominence of dual-retrieval distinctions in mainstream memory research, it is remarkable that the contributions of the two forms of retrieval to forgetting have been not extensively studied, and that their contributions to reminiscence have been completely ignored. With respect to forgetting, there is a conventional hypothesis—namely, that recollective retrieval is more prone to forgetting than nonrecollective retrieval, with forgetting being entirely recollective over intervals of a few days or a week (e.g., Gardiner & Java, 1991). However, the literature appears to contain no corresponding proposals about reminiscence. Further, extant data on the forgetting hypothesis are limited. Of the traditional metacognitive separation procedures, remember/know is the only one for which a moderate number of forgetting experiments has been reported. The data of those experiments generally show steeper declines over time in remember judgments than in know judgments (e.g., Barber, Rajaram, & Marsh, 2008; Sharot & Yonelinas, 2008; Viskontas, Carr, Engel, & Knowlton, 2009; Tunney, 2010; but cf. Gardiner & Java, 1991, Experiment 2), which is consistent with the conventional dual-retrieval hypothesis. However, the fact that there are numerous validity challenges to remember/know judgments (Donaldson, 1996; Dunn, 2004, 2008; Rotello et al., 2004) means that the data of remember/know forgetting studies cannot be interpreted as providing straightforward evidence for the notion that recollective retrieval fades more rapidly than nonrecollective retrieval.
In our research, we measured the contributions of recollective and nonrecollective retrieval to both forgetting and reminiscence. This was done by taking advantage of a property of the present model that was discussed earlier (footnote 1): Although items are assumed to absorb in state L during learning, this assumption depends on the continuation of learning trials. After learning trials cease, items that reached L may fall back to state P or state U over time, and of course, items that only reached P, which is not an absorbing state, may fall back to U over time. Such backward transitions are suggested by prior research on the dual-retrieval model in which, immediately following study-test trials, subjects performed additional recall tests without further opportunities to study the list (Brainerd, Payne, Wright, & Reyna, 2003). Over those tests, recollective retrieval declined substantially, indicating that L was no longer an absorbing state when study cyles were discontinued. Also, early work on two-stage Markov models of recall provided evidence of backward transitions from L and from P over retention intervals of one to two weeks (Brainerd et al., 1990).
This means that forgetting can be represented as the complement of learning via the same Markov chain; that is, learning is represented as forward transitions through the U-P-L state space, and forgetting is represented as backward transitions through the same space. Thus, as we shall see in greater detail in Experiments 3 and 4, the same parameters that are used to measure initial learning of the two forms of retrieval can be used to measure forgetting of the two forms of retrieval by fitting the same Markov model to a series of long-term retention tests, rather than to a series of learning trials. To pinpoint the retrieval loci of forgetting, one simply estimates the direct access, reconstruction, and familiarity judgment parameters on both occasions and determines their respective rates of decline over the interval between the learning trials and retention tests.
Turning to reminiscence, if subjects are administered a series of retention tests after a forgetting interval, it is well established that recall will recover, to some extent, as the tests proceed—usually by more than 10% (Brainerd & Reyna, 2005; Brainerd, Reyna, Howe, & Kingma, 1990; Howe & Brainerd, 1989). This is the phenomenon of reminiscence, which has been demonstrated for associative, cued, and free recall. In these experiments, “reminiscence” only refers to the recovery of performance for items that are actually retested, not to the recovery of performance for untested items as a function of retesting other items. Although the second type of recovery may also occur, particularly if semantically related lists are learned, the first type of recovery is the way that reminiscence has traditionally been studied. Because reminiscence has received no attention in research on dual-retrieval processes, the literature contains no theoretical proposals about whether it is due to test-induced recovery of recollective or nonrecollective retrieval ability. Hence, our research was designed to provide the first evidence on their relative contributions to reminiscence. Such evidence is reported in Experiments 3 and 4, which were continuations of Experiments 1 and 2, respectively. After completing Experiments 1 and 2, the subjects received additional study-test trials in order to achieve a perfect-recall criterion, and one-week later, they responded to a series of retention tests without additional study opportunities. As we shall see, the process loci of reminiscence can be determined in a manner that is similar to the procedure that was just described for determining the process loci of forgetting: One simply fits the Markov model to a series of long-term retention tests, estimates the direct access, reconstruction, and familiarity judgment parameters, and determines which of the processes recover as the tests proceed.
Experiments 1 and 2
Experiments 1 and 2 were focused on developmental theoretical questions, especially contrasting proposals about the relative contributions of recollective and nonrecollective retrieval to age improvements in episodic memory. As such proposals refer to developmental trends in initial learning, these experiments dealt with the learning side of dual-retrieval operations. The investigation of questions about forgetting and reminiscence is postponed to Experiments 3 and 4.
In the present experiments, children (7- and 8-year-olds) and adolescents (11- and 12-year-olds), learned lists of word pairs under standard associative recall procedures. Taxonomic relatedness of words was manipulated within each experiment, and the typicality of category exemplars was manipulated between experiments. Specifically, within each experiment, the lists of cue-target pairs that were administered to individual subjects consisted of (a) cues that were unrelated to each other and targets that were unrelated to each other (UU) or (b) cues that belonged to taxonomic categories (e.g., animals, clothing) and targets that were unrelated to each other (CU) or (c) cues that were unrelated to each other and targets that belonged to taxonomic categories (UC) or (d) cues that belonged to taxonomic categories and targets that belonged to other taxonomic categories (CC). Explicitly, the procedures for the two experiments were identical, except that all of the cues and targets in Experiment 1 were selected from among typical exemplars of familiar categories (production frequencies 1–8 of the Battig & Montague, 1969, norms) while all of the cues and targets in Experiment 2 were selected from among atypical exemplars of the same categories (production frequencies 9–16).
Beyond the contrasting proposals about overall developmental trends in dual-retrieval processes (Brainerd et al., 2009; Ghetti & Angelini, 2008), some predictions are possible about the taxonomic relatedness manipulation on the basis of past studies. As mentioned, adults’ associative recall is impaired when either cues or targets are taxonomically related, relative to lists in which they are unrelated (Underwood et al., 1965). We found in some recent experiments that this is because taxonomic relatedness impairs recollective retrieval, even though it enhances reconstruction and familiarity (Brainerd & Reyna, 2010). Developmentally, it is well established that the influence of taxonomic relatedness on recall waxes during childhood (e.g., Bjorklund, 1987), so one would predict that such effects should be more prevalent in adolescents than in children. Also, in adults, these effects are more pronounced with typical than with atypical category exemplars. Therefore, one would expect that the adult pattern of recollective and nonrecollective effects of taxonomic relatedness will be less apt to show up with atypical exemplars.
Method
Subjects
The subjects were 239 children (mean age = 8 years, 1 month, SD = .67 months; 119 males, 120 females) and 240 younger adolescents (mean age = 11 years, 11 months, SD = .67 months; half male, half female), who received parental permission to participate. (Although the original sample contained, 240 children, the data of one subject ultimately could not be used owing to failure to complete all of the recall trials.) Each subject at each age level was randomly assigned to Experiment 1 or Experiment 2, and within experiments, each subject was randomly assigned to one of four list conditions: unrelated cues and unrelated targets (UU), categorized cues and unrelated targets (CU), unrelated cues and categorized targets (UC), and categorized cues and categorized targets (CC). In Experiment 1, there were 120 children and 120 adolescents, divided among the four conditions. In Experiment 2, there were 119 children and 120 adolescents, divided among the four conditions.
Materials
The Battig and Montague (1969) norms were used to construct the lists of word pairs that the subjects in the two experiments learned to recall. In prior research, a large pool of words had been formed by sampling the 16 most frequent exemplars from several Battig-Montague categories (e.g., animals, clothing, flowers, fruit, furniture, musical instruments, and vehicles). For purposes of these two experiments, words from production frequencies 1–8 were designated “typical” and used to construct the lists in Experiment 1, while words from production frequencies 9–16 were designated “atypical” and used to construct the lists in Experiment 2. It should be noted that based on previous research, the atypical exemplars as well as the typical ones were all words that were known to the youngest subjects. The lists that were administered to individual subjects in each condition of each experiment consisted of 12 word pairs.
For subjects in the UU condition of each experiment, the lists administered to individual subjects were generated as follows. The 12 cue words were selected by randomly sampling one exemplar apiece from each of 12 different categories (typical exemplars in Experiment 1, atypical exemplars in Experiment 2), and the 12 target words were selected by randomly sampling one exemplar apiece from 12 other randomly selected categories (typical exemplars in Experiment 1, atypical exemplars in Experiment 2). All sampling from the Battig-Montague (1969) pool was without replacement. Lists were then constructed by randomly pairing the 12 cues with the 12 targets. For the UC, CU, and CC conditions, sampling from the Battig-Montague was again without replacement. For subjects in the UC condition of each experiment, the cue words were chosen in the same manner as in the UU condition, but the target words were chosen by randomly selecting 6 exemplars apiece (typical or atypical) from each of 2 categories from which no cue words had been selected. Lists were then constructed by randomly pairing each of the 12 cues with one of the 12 targets. For subjects in the CU condition, the target words were selected in the same manner as in the UU condition, but the cue words were chosen via the procedure that was used to choose target words in the UC condition. Lists were then constructed by randomly pairing each of the 12 cues with one of the 12 targets. Last, in the CC condition, the cue words were chosen by randomly selecting 6 exemplars apiece (typical or atypical) from each of 2 randomly selected categories, and the target words were chosen by randomly selecting 6 exemplars apiece from another 2 randomly selected categories. Lists were then constructed by randomly pairing each of the 12 cues with one of the 12 targets, subject to the constraint that 3 of the words in a given cue category were paired with 3 of the words in one of the target categories and the remaining 3 words in a given cue category were paired with 3 of the words in the other target category.
Procedure
The subjects were tested in small, quiet rooms within their respective schools. Following general memory instructions, subjects learned to recall their respective lists under oral associative recall conditions. The session consisted of three study-test trials. The complete sequence of events was S1B1AT1AB1BT1BS2B2T2S3B3T3, where each S denotes a study cycle on the list, each B denotes a 30 sec buffer activity, and each T denotes an oral associative recall test. Thus, the first study cycle was followed by two recall tests, whereas the other two were followed by one recall test apiece. The purpose of inserting two recall tests between the first and second study cycles was to provide an on-line measure of forgetting during learning; that is, to determine whether accuracy declines if each recall test is not followed by another study cycle and, if so, to determine which retrieval process is responsible. If accuracy had declined, it would have been necessary to introduce a forgetting parameter for test 1B (see Brainerd et al., 2009). In the event, reliable declines between test 1A and 1B were not observed at either age level: Average levels and conditions, levels of mean correct recall on test 1A versus 1B were 16% versus 17% in Experiment 1 and 22% versus 21% in Experiment 2. Hence, this matter is not considered in the report of results.
On study cycles, word pairs were visually presented (computer screen) in random order at a 5 sec rate, and both words were read aloud to the subject by the experimenter. Before each test trial, to eliminate short-term memory effects, the subject participated in 30 sec of letter shadowing. On recall tests, the cue word of each pair was visually presented in random order, read aloud by the experimenter, and the subject was allotted 3 sec to respond with a target word. This value was chosen because pilot research showed that when more than 3 sec was provided, there was only a 2% increase in recall and the preponderance of the responses were errors.
Results and Discussion
Preliminary Analysis
Before the retrieval model is used to test theoretical proposals about developmental change, we present some analysis of variance (ANOVA) results that provide targets for process explanations to aim at. The mean probabilities of correct recall for each experiment are reported by age level, cue condition, and target condition in Table 2. An important overall pattern, which will be exemplified by various ANOVA results, is that there are both basic similarities and key differences in the way that taxonomic relatedness affects the recall of children and adolescents versus adults. Here, it should be borne in mind that with adult subjects, categorizing either cues or targets impairs associative recall, with the effect being more pronounced on the cue sides of word pairs (Brainerd & Reyna, 2010; Underwood et al., 1965). In contrast, with children and adolescents, categorization did not invariably impair associative recall. In Experiment 1 (typical exemplars), it can be seen in Table 2 that adolescents’ performance resembled the adult pattern, in that taxonomic relatedness impaired recall on both sides of pairs, but in children, categorizing the cue sides of pairs actually improved recall when the targets were unrelated. In Experiment 2 (atypical exemplars), deviations from the adult pattern were more pronounced and occurred in adolescents as well as children. In children, categorizing the target sides of pairs always improved recall, regardless of whether cues were categorized or unrelated, while cue categorization did not have reliable effects. Adolescents’ performance also differed from the adult pattern, though less dramatically: Categorization always impaired recall on the cue side, but it improved recall on the target side when cues were categorized. The overall picture, then, was one of both qualitative developmental changes in the effects of categorization. With typical exemplars, categorization effects were qualitatively different for children than known effects for adults, and with atypical exemplars, categorization effects were qualitatively different for both children and adolescents than known effects for adults.
Table 2.
Mean Total Correct Recall in Experiments 1 and 2
| Age Level | ||
|---|---|---|
|
|
|
|
| Children | Adolescents | |
|
| ||
| Experiment 1 (typical) | ||
| Categorized cues: | ||
| Categorized targets | 10.77 | 13.87 |
| Unrelated targets | 20.57 | 21.47 |
| Unrelated cues: | ||
| Categorized targets | 14.40 | 21.63 |
| Unrelated targets | 15.93 | 27.13 |
| Means | 15.42 | 21.03 |
|
| ||
| Experiment 2 (atypical) | ||
|
| ||
| Categorized cues: | ||
| Categorized targets | 16.07 | 17.63 |
| Unrelated targets | 12.31 | 12.90 |
| Unrelated cues: | ||
| Categorized targets | 16.53 | 20.43 |
| Unrelated targets | 13.90 | 23.70 |
| Means | 14.70 | 18.67 |
To provide statistical support for this picture, we computed a 2 (age: children versus adolescents) × 2 (cues: categorized versus unrelated) × 2 (targets: categorized versus unrelated) ANOVA of total correct recall for both experiments. In Experiment 1, there were main effects for age, F (1, 232) = 28.22, MSE = 66.88, p < .0001, cue, F (1, 232) = 8.67, MSE = 66.88, p < .004, and target, F (1, 232) = 33.47, MSE = 66.88, p < .0001. As can be seen in Table 2, total recall was better, on average, for adolescents, for unrelated cues, and for unrelated targets. However, the cue effect was qualified by an Age X Cue interaction, F (1, 232) = 11.68, MSE = 66.88, p < .001, and the target effect was qualified by a Cue X Target interaction, F (1, 232) = 6.03, MSE = 66.88, p < .02. We parsed both interactions with appropriate post hoc tests (Tukey HSD), which produced simple patterns (all differences significant at or beyond the .05 level). The reason for the Age X Cue interaction is although cue categorization reduced recall in both the CC-UC and CU-UU comparisons with adolescents and in the CC-UC comparison with children, it increased recall with children in the CU-UU comparison. The reason for the Cue X Target interaction is that although categorizing the target sides of pairs impaired recall, on average, in both the CC-CU and UC-UU comparisons, the impairment was more than twice as large in the CC-CU comparison.
In Experiment 2, where the lists were composed of less familiar words, the ANOVA results differed in important respects from those of Experiment 1. There were main effects for age, F (1, 232) = 16.67, MSE = 56.30, p < .0001, cue, F (1, 232) = 16.26, MSE = 56.30, p < .0001, and target, F (1, 232) = 4.09, MSE = 56.30, p < .05. It can be seen in Table 2 that although total recall was again better, on average, for adolescents and for unrelated cues, and it was now better on average for categorized targets. As in the first experiment, the cue effect was qualified by an Age X Cue interaction, F (1, 232) = 8.34, MSE = 56.30, p < .003, and the target effect was qualified by a Cue X Target interaction, F (1, 232) = 5.52, MSE = 56.30, p < .02. We parsed these interactions with appropriate post hoc tests, as before, and the patterns were as follows. The reason for the Age X Cue interaction is although cue categorization reduced recall reliably in both the CC-UC and CU-UU comparisons with adolescents, it did not affect children’s recall. The reason for the Cue X Target interaction is that the target categorization effect depended upon cue categorization. Specifically, categorized targets produced better recall, on average, when cues were categorized but did not have a reliable overall effect when cues were unrelated.
In sum, associative recall improved with development for typical and atypical lists, but the effects of taxonomic relatedness (a) differed qualitatively from the standard patterns in adults and (b) differed for typical versus atypical materials. Concerning a, while taxonomic relatedness impairs adults’ recall on both the cue and target sides of pairs, it did not always do so in children and adolescents. Indeed, it sometimes improved recall and sometimes failed to affect recall. Concerning b, cue and target effects for adolescents were qualitatively similar to adults’ with typical materials (Experiment 1), and children displayed the adult pattern on the target side. With atypical materials (Experiment 2), however, both children and adolescents exhibited taxonomic relatedness effects on the target side when cues were categorized that were the reverse of the adult pattern.
Model Results
We report the model analyses in two waves. First, we consider the baseline question of whether the dual-retrieval model fits the associative recall data of children and adolescents. Second, we estimate the model’s direct access, reconstruction, and familiarity judgment parameters in order to explain developmental changes in the overall accuracy of recall and in the effects of taxonomic relatedness and typicality.
Fit
Two questions about fit must be answered, one about necessity and the other about sufficiency (Brainerd & Reyna, 2010). The necessity question asks whether the dual-retrieval model is not parsimonious because the data are well fit by a simpler model with only a single nonrecollective retrieval process or a single recollective process. Both of these one-process models are shown in the Appendix, in Equations A12 and A14, along with their corresponding fit tests (Equations A13 and A15). These tests were conducted for all of the Age X Condition cells of the present experiments. The results are reported in the Appendix, where it can be seen that both one-process models were rejected at high levels of confidence; that is, the data violated the assumption that recall was based on a single retrieval process.
Turning to the sufficiency question, this question asks whether associative recall data are more complex than the dual-retrieval model supposes and that, therefore, such data are not well fit by that model. The appropriate fit test, which was conducted for all of the Age X Condition cells of the present experiments, is shown in Equation A11. The results are reported in the Appendix, where it can be seen that the two-process model could not be rejected in either experiment; that is, the data did not violate the assumption that recall was based on two retrieval processes.
Parameter analyses: Process explanations of developmental trends
Values of the parameters that measure recollective and nonrecollective retrieval are displayed in Table 3, where these values are exhibited separately by experiment, age level, cue relatedness, and target relatedness. As just mentioned, there are two ways to fit the model to a sequence of three study-test trials in each experiment, and parameter values are reported separately for each sequence in Table 3.
Table 3.
Estimates of the Dual-Retrieval Model’s Parameters for Experiments 1 and 2
| Age and relatedness | Recollection
|
Reconstruction
|
Familiarity judgment
|
|||
|---|---|---|---|---|---|---|
| D1 | D2 | R1 | R2 | J1 | J2 | |
|
| ||||||
| Experiment 1 (typical exemplars) | ||||||
| First estimation | ||||||
| Adolescents: | ||||||
| UU | .25 | .46 | .11 | .43 | .98 | .52 |
| CU | .20 | .33 | .14 | .20 | .15 | .12 |
| UC | .23 | .33 | .15 | .27 | .16 | .46 |
| CC | .09 | .19 | .39 | .03 | .21 | .31 |
| Means | .19 | .33 | .21 | .21 | .38 | .36 |
| Children: | ||||||
| UU | .10 | .23 | .13 | .79 | .34 | .12 |
| CU | .12 | .34 | .18 | .15 | .67 | .66 |
| UC | .10 | .23 | .42 | .69 | .10 | .12 |
| CC | .07 | .16 | .26 | .01 | .19 | .42 |
| Means | .10 | .24 | .25 | .41 | .33 | .33 |
| Second estimation | ||||||
| Adolescents: | ||||||
| UU | .27 | .48 | .12 | .56 | .98 | .35 |
| CU | .20 | .28 | .08 | .24 | .98 | .69 |
| UC | .22 | .34 | .21 | .22 | .11 | .46 |
| CC | .08 | .13 | .25 | .12 | .31 | .63 |
| Means | .19 | .31 | .17 | .29 | .60 | .53 |
| Children: | ||||||
| UU | .13 | .12 | .09 | .29 | .46 | .68 |
| CU | .13 | .32 | .13 | .19 | .99 | .72 |
| UC | .13 | .20 | .06 | .30 | .45 | .33 |
| CC | .05 | .15 | .25 | .01 | .16 | .50 |
| Means | .11 | .20 | .13 | .19 | .52 | .56 |
|
| ||||||
| Experiment 2 (atypical exemplars) | ||||||
|
| ||||||
| First estimation | ||||||
| Adolescents: | ||||||
| UU | .23 | .44 | .34 | .49 | .13 | .22 |
| CU | .09 | .18 | .02 | .49 | .98 | .27 |
| UC | .20 | .23 | .09 | .44 | .99 | .44 |
| CC | .17 | .06 | .16 | .22 | .50 | .80 |
| Means | .17 | .23 | .15 | .41 | .65 | .43 |
| Children: | ||||||
| UU | .11 | .15 | .24 | .09 | .12 | .58 |
| CU | .10 | .20 | .11 | .29 | .11 | .29 |
| UC | .14 | .16 | .08 | .32 | .99 | .55 |
| CC | .14 | .06 | .32 | .05 | .33 | .77 |
| Means | .12 | .14 | .19 | .19 | .41 | .55 |
| Second estimation | ||||||
| Adolescents: | ||||||
| UU | .25 | .40 | .14 | .30 | .19 | .47 |
| CU | .07 | .11 | .02 | .32 | .99 | .63 |
| UC | .18 | .22 | .09 | .41 | .99 | .52 |
| CC | .19 | .15 | .18 | .14 | .37 | .64 |
| Means | .17 | .22 | .17 | .29 | .64 | .57 |
| Children: | ||||||
| UU | .11 | .19 | .34 | .01 | .12 | .04 |
| CU | .09 | .21 | .27 | .06 | .07 | .29 |
| UC | .13 | .14 | .06 | .32 | .98 | .62 |
| CC | .16 | .10 | .32 | .00 | .28 | .07 |
| Means | .12 | .16 | .25 | .08 | .36 | .26 |
Why was recall always more accurate in adolescents than in children? We saw that according to one hypothesis, improvements in episodic memory during childhood are wholly matters of improved recollective retrieval. According to another hypothesis, however, improvements in episodic memory are due to both recollective and nonrecollective retrieval, with improvements in the former being more important with some types of tasks and improvements in the latter being more important with other types of tasks. To evaluate these hypotheses, we examined age differences in the D, R, and J parameters across the various conditions of Experiments 1 and 2. Although we shall see that the data favored the second hypothesis, first we briefly explicate the method of analysis.
Naturally, age differences in the D parameters were used to test for developmental improvements in recollective retrieval, whereas age differences in the R and J parameters were used to test for developmental improvements in nonrecollective retrieval. Age differences in all of these parameters were tested for significance in the same way, using the appropriate likelihood ratio test (Brainerd et al., 2009). Statistical methods for testing within- and between-condition hypotheses about parameter values with likelihood ratios are elaborated in the Appendix (see Equations 11–11c). Whenever values of a target parameter for a given condition are being compared for two age levels, this test generates a G2 statistic with 1 degree freedom, whose asymptotic distribution is therefore χ2(1) with a critical value of 3.84 to reject the null hypothesis. (The null hypothesis is that the target parameter has the same value for both groups.) When this test was computed for the D, R, and J parameters in Table 3, a simple pattern emerged. (In these and all other parametric analyses of effects that are reported in this paper, in order to simplify the presentation, we omit discussion of parameters that did not produce reliable differences.)
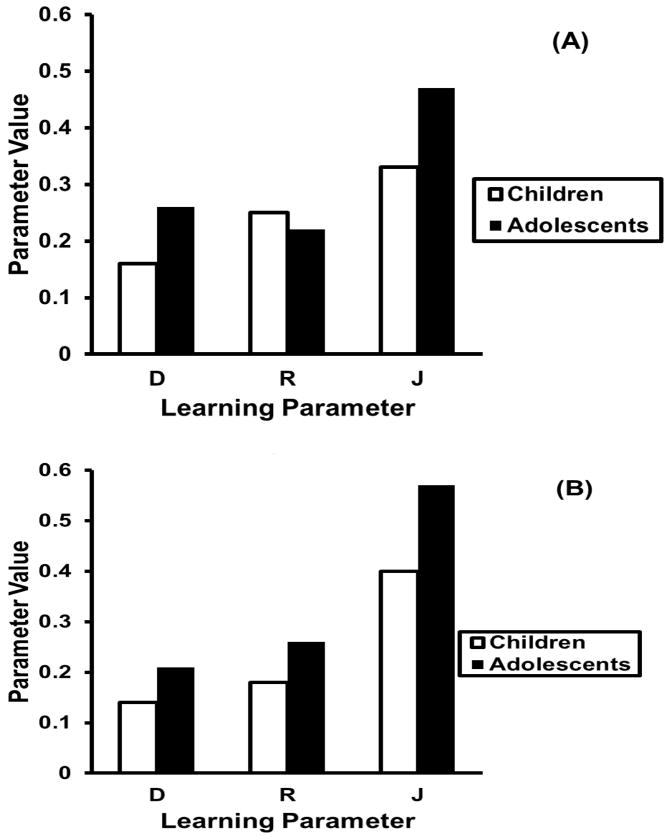
First, in Experiment 1, where lists were composed of very familiar words, such as coat and horse, age improvements in recall were dominated by developmental changes in recollective retrieval. Pooling over conditions and the two sets of estimates, the mean values of the two recollection parameters, D1 and D2, were .11 and .22, respectively for children, which rose to .20 and .32, respectively, for adolescents. For each of these two parameters, it was possible to compute four likelihood ratio tests for the first set of parameter estimates (Trials 1A-2-3) and four likelihood ratio tests for the second set (Trials 1B-2-3). Each of these tests was computed separately, for a total of 16 tests in all, though naturally there are statistical dependencies between the first and second sets of tests because there is some overlap in the data that are used. For D1, the G2(1) statistic produced a null hypothesis rejection for four of the eight tests, and for D2, the G2(1) statistic also produced a null hypothesis rejection for four of the eight tests. Turning to the reconstruction parameters, there was little developmental change, the overall mean values of R1 and R2, respectively, being .19 and .30 for children versus .19 and .25 for adolescents. Likewise, for familiarity judgment, there was little developmental change, the overall mean values of J1 and J2, respectively, being .43 and .46 for children versus .49 and .45 for adolescents.
Second, in Experiment 2, where lists were composed of less familiar words (e.g., blouse and moose) age improvements in recall were dominated by developmental changes in reconstruction and familiarity judgment. Concerning recollection, there were small overall differences favoring adolescents, the mean values of D1 and D2, respectively, being .11 and .15 for children versus .17 and .23 for adolescents. Befitting these small differences, only one of the eight G2(1) tests for developmental differences in D1 and one of the eight tests for developmental differences in D2 produced null hypothesis rejections. Concerning reconstruction, although the overall mean values of R1 were similar for the two age levels (.22 versus .16), the overall mean value of R2 was much larger for adolescents than for children (.35 versus .14). Seven of the eight G2(1) tests for developmental differences in R2 produced null hypothesis rejections. Last, concerning familiarity judgment, the overall mean values of J1 and J2, respectively, were .38 and .37 for children versus .65 and .50 for adolescents. Four of the eight G2(1) tests for developmental differences in J1 produced null hypothesis rejections favoring adolescents, and three of the corresponding tests for J2 produced such rejections.
To summarize, the developmental portion of the modeling results is shown in Figure 1, with mean parameter values for Experiment 1 appearing in Panel A and mean values for Experiment 2 appearing in Panel B. As can be seen, overall, the modeling results were consistent with the second hypothesis that we discussed earlier, in that there was evidence that (a) recollection, reconstruction, and familiarity judgment all contribute to improvements in recall but (b) which process dominates age improvements varies as a function of task demands. In this instance, the task variable was the typicality of the materials.
Figure 1.
Developmental trends in direct access (parameter D), reconstruction (parameter R), and familiarity judgment (parameter J) during the learning phase. Experiment 1 (typical exemplars) results appear in Panel A. Experiment 2 (atypical exemplars) results appear in Panel B.
Parameter analyses: Process explanations of taxonomic relatedness and typicality effects
First, we consider how taxonomic relatedness affected the retrieval processes at each age level, in both experiments. Typicality effects will then emerge as differences between the process-level effects in the respective experiments.
1. Target relatedness
In Experiment 1, it will be remembered that the ANOVA showed that categorized targets produced poorer recall than unrelated targets at both age levels. Why? In children the effect was nonrecollective—specifically, it was both a reconstruction and a familiarity judgment effect. Pooling over conditions and the two sets of estimates, the overall means for word pairs with categorized versus unrelated targets were .25 versus .36 for R2, .22 versus .36 for J1, and .34 versus .55 for J2. Thus, after Trial 1, children were better at reconstructing unrelated targets than categorized targets, and once such targets were reconstructed, they were more likely to be judged familiar enough to output. For each of these three parameters, it was possible to compute four G2(1) tests of the null hypothesis that parameter values were the same for categorized versus unrelated targets, and for each parameter, three of the four tests produced a null hypothesis rejection. Concerning adolescents, reconstruction and familiarity judgment were also responsible for the target categorization effect in these subjects, but recollection also contributed. As in children, the overall mean values of R2 and J1 were larger for pairs with unrelated targets (R2 means = .36 and .16, J1 means = .77 and .20.) (All four G2(1) tests for R2 and three of the four tests for J1 produced null hypothesis rejections.) In addition, however, the overall mean value of D2 was larger for pairs with unrelated targets (.39 versus .25), and three of the four G2(1) tests produced null hypothesis rejections. Note that this explains the earlier finding that the effects of target categorization, though qualitatively the same at the two age levels, were larger in adolescents: Target categorization only affected nonrecollective retrieval in children but affected recollective as well as nonrecollective retrieval in adolescents.
Turning to Experiment 2, target relatedness improved, rather than impaired, children’s recall with atypical materials. This was a pure familiarity effect. The overall mean values of J1 and J2 were larger for pairs with categorized targets (J1 = .65 and J2 = .50) than for pairs with unrelated targets (J1 = .11 and J2 = .31). (All four G2(1) tests for J1 and two of the four tests for J2 produced null hypothesis rejections.) With adolescents, on the other hand, remember that there was a Cue X Target cross-over, with categorized targets (a) improving recall when cues were categorized but (b) impairing recall when cues were unrelated. Effect a was both recollective and reconstructive. When cues were categorized, the overall mean values of D1 and R1 were larger for pairs with categorized targets (D1 = .18 and R1 = .17) than for pairs with unrelated targets (D1 = .08 and R1 = .02). (One of the two G2(1) tests for D1 and both of the tests for R1 produced null hypothesis rejections.) Effect b was both recollective and reconstructive, too. When cues were unrelated, the overall mean values of D2 and R1 were larger for pairs with unrelated targets (D2 = .42 and R1 = .24) than for pairs with categorized targets (D2 = .23 and R1 = .09). (One of the two G2(1) tests for R1 and both of the tests for D2 produced null hypothesis rejections.)
Summing up, the parameter analyses revealed three things of general significance about target categorization effects. First, categorizing the target sides of pairs is first and foremost a nonrecollective effect. This manipulation always affected the reconstruction or familiarity judgment parameters. Second, the direction of this effect depended on the typicality of the materials. With typical materials, categorized targets impaired reconstruction and familiarity judgment at both age levels, but with atypical materials, categorized materials enhanced familiarity judgment in children and enhanced reconstruction in adolescents when cues were categorized. Third, target categorization effects were recollective as well as nonrecollective in adolescents, as they are in adults (Brainerd & Reyna, 2010), but not in children.
2. Cue relatedness
In Experiment 1, it will be remembered that the ANOVA showed that categorized cues always produced poorer recall than unrelated cues in adolescents and also produced poorer recall in children when targets were categorized. In adolescents, the effect was primarily recollective. As happens with adult subjects, the values of the two recollection parameters were lower for pairs with categorized cues than for pairs with unrelated cues (D1 means = .14 and .24, D2 means = .23 and .40.), (All four G2(1) tests for D2 and two of the four tests for D1 produced null hypothesis rejections.) Reconstruction also contributed to the effect in that R2 was lower for pairs with categorized cues than for pairs with unrelated cues (means = .15 and .37). (All four G2(1) tests produced null hypothesis rejections.) In children, the tendency of categorized cues to impair recall when targets were categorized was a pure reconstruction effect: R2 was lower for pairs with categorized cues than for pairs with unrelated cues (means = .50 and .01). (Both G2(1) tests produced null hypothesis rejections.) Finally, the fact that categorized cues improved children’s recall when targets were unrelated was primarily a familiarity judgment effect in that the values of these two parameters were lower for pairs with unrelated cues than for pairs with categorized cues (J1 means = .40 and .83, J2 means = .40 and .69.), (Both G2(1) tests for J1 and one of the two tests for J2 produced null hypothesis rejections.)
In Experiment 2, as in Experiment 1, the ANOVA showed that categorized cues always produced poorer recall than unrelated cues in adolescents, whereas categorizing the cue sides of pairs had no effect on children’s recall. The explanation of the adolescent effect was the same as in Experiment 1—namely, it was chiefly a recollection effect, with some contribution from reconstruction as well. The two recollection parameters were smaller for pairs with categorized cues than for pairs with unrelated cues (D1 means = .13 and .22, D2 means = .13 and .33). (Three of the four G2(1) tests for D2 and two of the four tests for D1 produced null hypothesis rejections.) Also, one of the reconstruction parameters, R2, was smaller for pairs with categorized cues than for pairs with unrelated cues (means = .29 and .41). (Two of the four G2(1) tests produced null hypothesis rejections.)
In sum, the parameter analyses revealed that the effects of categorizing the cue sides of pairs were different for adolescents versus children. Adolescent data resembled prior findings with adults inasmuch as cue categorization suppressed recollective retrieval, regardless of whether exemplars were typical or atypical. However, unlike prior adult findings, cue categorization also suppressed reconstruction with both typical and atypical exemplars, though this effect was modest in comparison to recollective suppression. Cue categorization effects in children were qualitatively different than adult effects. Cue categorization had no impact when exemplars were atypical, and when they were typical, it sometimes improved recall by enhancing familiarity judgment. In sharp contrast to adult findings (Brainerd & Reyna, 2010), there was no evidence that cue categorization affected children’s recollective retrieval.
3. Typicality
The manner in which typicality modified the process-level effects of taxonomic relatedness emerges as differences in the parametric effects of the cue and target manipulations in Experiment 1 (typical) versus Experiment 2 (atypical). There were both qualitative and quantitative differences. The qualitative differences were observed for target relatedness. With typical exemplars, categorizing the target sides of word pairs impaired reconstruction and made reconstructed items seem less familiar. With atypical exemplars, however, it enhanced familiarity judgment in children and enhanced reconstruction in adolescents. Quantitative differences were observed for cue relatedness. Specifically, the suppressive effects on reconstruction and recollection that were observed at both age levels with typical materials, were not observed in children with atypical materials. We postpone analysis of the larger theoretical implications of typicality effects until the General Discussion, where they are considered in light of what is known about the development of taxonomic organization in memory.
Experiments 3 and 4
We turn now to two core topics in episodic memory that have not figured centrally in the study of dual-retrieval operations: forgetting and reminiscence. We investigated differences in forgetting and reminiscence for recollective versus nonrecollective retrieval, using the same recall tasks, list manipulations, and subjects as in the first two experiments. In order to conduct these experiments, the subjects in the first two experiments participated in a series of long-term retention tests one week after they had participated in a criterion-learning procedure that made their recall errorless.
As we previously saw, there is a conventional hypothesis about forgetting of dual-retrieval operations, which posits that recollective retrieval fades more rapidly than nonrecollective retrieval (Gardiner & Java, 1991). As we also saw, of the traditional recognition-based separation procedures, reminiscence has not been investigated with any of them, and remember/know is the only one for which a moderate number of forgetting experiments has been conducted. Further, although the latter experiments have generally shown higher rates of decline for remember than for know judgments (e.g., Barber, Rajaram, & Marsh, 2008; Sharot & Yonelinas, 2008; Tunney, 2010; Viskontas, Carr, Engel, & Knowlton, 2009), the many published validity challenges to such judgments make interpretation of this pattern uncertain.
In the present experiments, we measured differences in the susceptibility of the two forms of retrieval to forgetting, while taking into account differences in their initial levels of learning. More explicitly, we measured declines in recollective and nonrecollective retrieval after a forgetting interval, and we expressed those declines as functions of their levels of learning at the start of the interval. This is easily done with the dual-retrieval model, especially when criterion-learning occurs before the forgetting interval ensues. Remember that under the model, errorless recall is supported by recollection but not by reconstruction. Consequently, requiring that all subjects meet a stringent acquisition criterion, such as two or more consecutive errorless recall tests, forces all items to enter state L of the model (recollective retrieval), but it does not force them to enter state P (reconstructive retrieval). On the contrary, it is clear from Equation A1 that because items absorb in the errorless recollective state L, the only ones that subjects learn to reconstruct are those that they do not first learn how to recollect. Under the model, then, criterion learning ensures that recollective learning is complete, in the sense that all items are forced into state L, but reconstructive learning is not complete because items do not have to enter state P before entering L.2 This means that items that have entered L by the end of the learning phase are of two types: those that subjects also learned to reconstruct (U → P → L items) and those that they did not learn to reconstruct (U → L items).
Thus, declines in recollection over a forgetting interval can be measured by simply estimating the parameter D1 at the end of the forgetting interval, with the quantity 1−D1 serving as the measure of forgetting. (To avoid confusion, the subscript f will be appended whenever a parameter is estimated after a forgetting interval, so that the measure of recollective forgetting is denoted 1−D1f.) In order to estimate declines in reconstruction, on the other hand, one must take account of the fact that there are two types of items for which reconstructive forgetting can occur: Items that reached L after subjects learned to reconstruct them (U → P → L items) and items that subjects learned to reconstruct but not to recollect (U → P items). In order to estimate declines in reconstruction, then, estimates of the reconstruction parameter at the end of the forgetting interval (i.e., R1f) must be compared to the proportion of items that subjects learned to reconstruct during the acquisition phase (i.e., the total proportion of the above two item types). That is done as follows.
In Equation A1, it is easy to see that the probability that subjects learned to reconstruct an item on the first acquisition trial is (1−D1)R1. Algebraic manipulation of Equation A1 reveals that thereafter, the probability that subjects learned to reconstruct an item on any trial i > 1 is given by the expression [(1−D1)(R11−R1) R1Σ (1−D2)i−1(1−R2)i−2]. Thus, in a given condition, if k acquisition trials are required for a subject to reach criterion, the proportion of items that the subject learned to reconstruct during the course of acquisition is
| (1) |
The measure of forgetting, then, is P(R) − R1f. An important implication of Equation 1 is that as long as the values of D1 and D2 are not very small, the proportion of items that subjects learn to reconstruct during the acquisition phase will be far from unity. To illustrate this point, consider the data of the adolescent subjects in Experiment 1. Averaging over the four list conditions, the mean values of the four parameters in Equation 1 are D1 = .19, R1 = .19, D2 = .22, and R2 = .25. Consider a hypothetical subject who required 10 trials to reach criterion. The value of the (1−D1)R1 term in Equation 1 is .15 and the value of the (1−D1)(1−R1) R1Σ (1−D2)i−1(1−R2)i−2 term is .23, so that the proportion of items that these subjects had learned to reconstruct by the end of acquisition is .38.
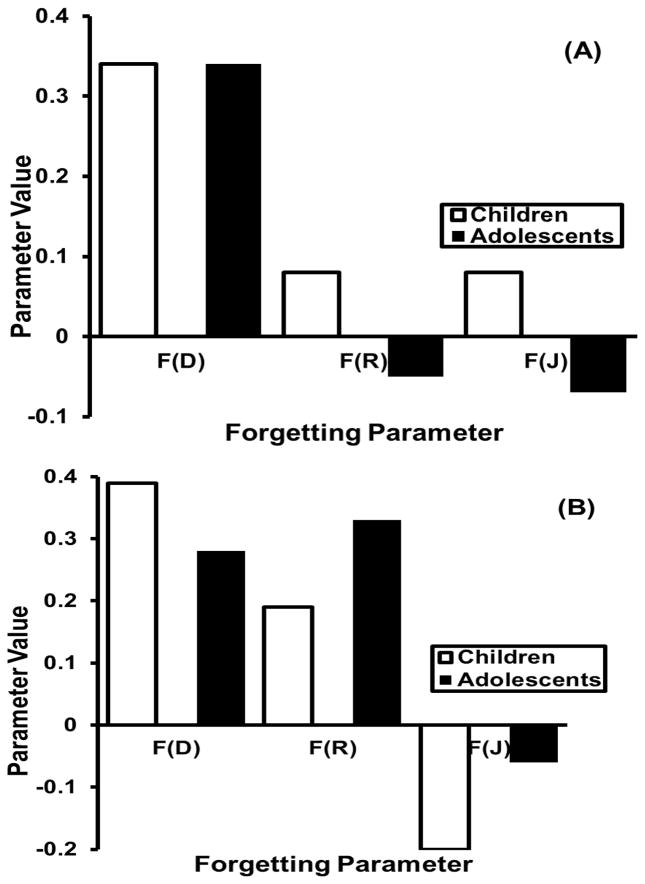
Because nonrecollective recall depends jointly on the reconstruction operation and the slave familiarity judgment operation, declines in the latter are also a form of nonrecollective forgetting. In the model, J2 is the probability after Trial 1 that a reconstructed item passes the familiarity check and is actually recalled. If we let J1f denote the probability that reconstructed items pass the familiarity check at the end of the forgetting interval, J2 − J1f measures declines in familiarity judgment over forgetting intervals. In Experiments 3 and 4, the quantities 1 − D1f, P(R) − R1f, and J2 − J1f were used to measure forgetting of recollective and nonrecollective retrieval for the different age levels and list conditions of the first two experiments.
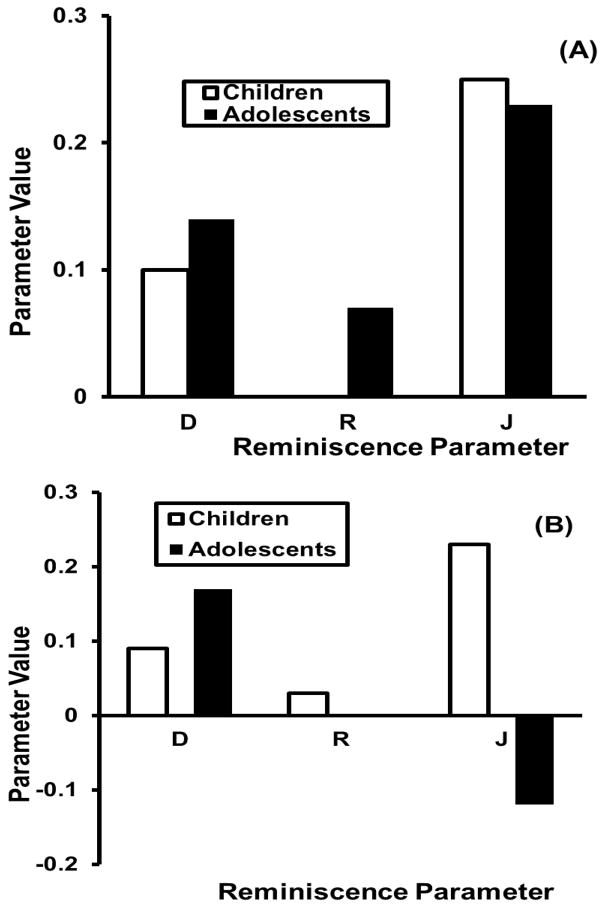
One focus of these experiments was therefore on forgetting—more particularly, on how recollective and nonrecollective retrieval processes contribute to declines in recall and to differences in those contributions as functions of development and taxonomic relatedness. However, we also investigated the complementary phenomenon of reminiscence; the ubiquitous tendency of recall to recover over a series of retention tests, usually by more than 10%. Naturally, we were interested in whether rates of reminiscence over retention tests varied as functions of development and taxonomic relatedness. However, our primary interest attached to the more fundamental question of the process explanation of reminiscence. Because the retention data were analyzed with the same model that was used to analyze the acquisition data of Experiments 1 and 2, the reminiscence effect in any condition could be parsed into its recollective, reconstructive, and familiarity components. Thus, it was possible to enquire about the process reasons for reminiscence effects in general (recollection? reconstruction? familiarity judgment?) and also as functions of development and of taxonomic relatedness. To the best our knowledge, such questions have not been previously investigated.
Method
Subjects
The subjects in Experiment 3 were the same 120 children and 120 adolescents who participated in Experiment 1. The subjects in Experiment 4 were the same 119 children and 120 adolescents who participated in Experiment 2.
Materials
The lists in Experiment 3 were the same as in Experiment 1. The lists in Experiment 4 were the same as in Experiment 2.
Procedure
It will be remembered that in Experiments 1 and 2, the subjects at both age levels completed the three trial sequence S1T1AT1B S2T2S3T3 on the lists for their respective conditions (UU, CU, UC, and CC). After the completion of this sequence, each subject participated in further study-test trials on his or her list. Those trials continued until the subject reached a criterion of two consecutive errorless recall tests on his or her list. All 479 subjects were able to meet this criterion. The modal number of additional cycles to reach criterion was two for the adolescents and four for the children.
One week later, all 479 subjects participated in long-term retention tests, which consisted of a series of five separate associative recall tests like those that were administered during the acquisition phase but without further opportunities to study the lists. At the start of the retention session, subjects received instructions for the upcoming tests. They were reminded that they had learned to recall a list of word pairs one week earlier and that the purpose of the retention session was to determine how many of those pairs they could still remember. They were then told that they would receive a few memory tests, like those to which they had previously responded, but not the exact number. The first test was then administered, following the same procedure as one week earlier. The first test was followed by a 30 sec buffer activity, using the same procedure as one week earlier. This procedure of alternating recall tests and buffer activity continued until five recall tests had been administered. Thus, following instructions, the complete sequence of test and buffer events for all subjects was T1B1T2B2T3B3T4B4T5.
Results and Discussion
Preliminary Analysis
As before, we begin with ANOVA results that provide targets for process explanation to aim at. The mean probabilities of correct recall for each experiment are displayed in Table 4 by age level, cue condition, target condition and retention test. It should be noted in connection with these probabilities that intrusions were rare. Less than 2% of the errors were intrusions; over 98% of errors consisted of providing no response to test cues.
Table 4.
Correct Recall Probabilities in Experiments 3 and 4
| Retention test | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
|||||||||||
| Children | Adolescents | |||||||||||
| 1 | 2 | 3 | 4 | 5 | M | 1 | 2 | 3 | 4 | 5 | M | |
|
| ||||||||||||
| Experiment 3 (typical) | ||||||||||||
| Cat. cues: | ||||||||||||
| Cat. targets | .66 | .74 | .83 | .83 | .84 | .78 | .61 | .74 | .73 | .82 | .84 | .75 |
| Un. targets | .71 | .78 | .80 | .81 | .81 | .78 | .72 | .78 | .80 | .81 | .74 | .77 |
| Un. cues: | ||||||||||||
| Cat. targets | .72 | .84 | .84 | .85 | .88 | .83 | .73 | .89 | .90 | .90 | .91 | .87 |
| Un. targets | .70 | .77 | .80 | .83 | .84 | .79 | .81 | .84 | .86 | .88 | .88 | .85 |
|
| ||||||||||||
| Experiment 4 (atypical) | ||||||||||||
|
| ||||||||||||
| Cat. cues: | ||||||||||||
| Cat. targets | .44 | .51 | .56 | .57 | .57 | .52 | .59 | .67 | .70 | .72 | .71 | .68 |
| Un. Targets | .68 | .72 | .75 | .78 | .78 | .74 | .77 | .80 | .83 | .83 | .86 | .82 |
| Un. cues: | ||||||||||||
| Cat. targets | .84 | .89 | .90 | .84 | .93 | .88 | .73 | .88 | .90 | .90 | .91 | .86 |
| Un. Targets | .71 | .76 | .80 | .80 | .80 | .77 | .79 | .83 | .86 | .88 | .89 | .85 |
To measure age and treatment differences in forgetting rates, we computed 2 (age) × 2 (cue relatedness) × 2 (target relatedness) ANOVAs of total correct recall on the first retention test. Because reminiscence is ubiquitous over a sequence of long-term retention tests (e.g., Brainerd et al., 1990), it was necessary to restrict these ANOVAs to the first test, in order to avoid confounding forgetting with reminiscence. In Experiment 3 (typical exemplars), the ANOVA produced a main effect for cue relatedness, F (1, 232) = 10.21, MSE = 4.64, p < .0001, and a Cue X Target interaction, F (1, 232) = 15.19, MSE = 4.64, p < .0001. The cue effect was due to the fact that forgetting rates were higher for pairs with categorized cues than for pairs with unrelated cues, at both age levels. This parallels the learning effect of cue categorization and is more consistent than the learning effect (categorized cues did not impair children’s learning when targets were unrelated). As before, we parsed the Cue X Target interaction with Tukey HSD tests and noted a simple pattern: The forgetting rate was higher for categorized targets when cues were categorized but was higher for unrelated targets when cues were unrelated. Note that this cross-over is in same direction as the Cue X Target interaction in the learning data—where categorizing the target sides of pairs always impaired learning, but the impairment was much larger when cues were categorized than when they were unrelated. In Experiment 4 (atypical exemplars), the ANOVA produced only a main effect for age, F (1, 231) = 4.01, MSE = 4.64, p < .05, such that forgetting rates were higher for children than for adolescents. Hence, typicality effects on forgetting were dramatic in that taxonomic relatedness only affected forgetting when materials were typical, and forgetting only declined with age when materials were atypical.
Turning to reminiscence, we computed a 2 (age) × 2 (cue relatedness) × 2 (target relatedness) × 5 (retention test) ANOVA of total correct recall, with repeated measures on the last factor. Here, the results of interest are the retention test main effect, which measures whether reminiscence effects were reliable, together with interactions of the retention test factor with the other three factors, which measure whether reminiscence rates varied as functions of age, cue relatedness, or target relatedness. There was robust reminiscence in Experiment 3, as indicated by a large main effect for retention test, F(4, 696) = 104.32, MSE = 1.03, p < .0001, such that recall improved over the five tests by an average of 18%. This reminiscence effect interacted with the type of target, F (4, 696) = 11.61, MSE = 1.03, p < .0001. Over tests, reminiscence was more pronounced for categorized targets than for unrelated targets. In other words, although children and adolescents were good at recovering the ability to recall forgotten targets when the targets were unrelated (12% reminiscence), they were especially good when forgotten targets were categorized (28% reminiscence). Note, here, the dissociation between reminiscence and learning: Whereas categorizing the cue sides of pairs always impaired subjects’ ability to learn to recall targets, it enhanced their ability to reminisce targets after a forgetting interval. Turning to Experiment 4, the ANOVA results for atypical exemplars revealed broader effects of taxonomic relatedness than in Experiment 3. To begin, however, robust reminiscence was again present, as indicated by a large retention test main effect, F (4, 695) = 79.92, MSE = .90, p < .0001, with recall increasing by 13% on average between the first and fifth test. As in Experiment 3, retention test did not interact with age (F < 1); children were able to recover forgotten items as readily as adolescents, for atypical as well as typical materials. Also as in Experiment 3, the reminiscence effect interacted with the type of target, F (4, 695) = 8.51, MSE = .90, p < .001. Post hoc tests again revealed that there was more total reminiscence for categorized than for unrelated targets. Unlike Experiment 3, the reminiscence effect interacted with the type of cue, F (4, 695) = 7.61, MSE = .90, p < .003. Post hoc tests revealed that there was more total reminiscence for categorized than for unrelated cues.
With respect to the overall forgetting picture for associative recall, because all subjects had achieved errorless performance a week earlier, the amount of forgetting in each cell of Table 4 is simply the difference between the recall probability in that cell and unity. Pooling over list conditions, the amount of forgetting, before reminiscence had a chance to operate, was 31% for children in Experiment 3, 28% for adolescents in Experiment 3, 33% for children in Experiment 4, and 28% for adolescents in Experiment 4. By the final retention test, when reminiscence had operated maximally, the residual amounts of forgetting were 16% for both children and adolescents in Experiment 3, 23% for children in Experiment 4, and 16% for adolescents in Experiment 4. In sum, the amount of forgetting following criterion learning was quite substantial, averaging 30% over age levels, experiments, and list conditions, but the amount of reminiscence over the five retention tests was also quite substantial, averaging 18% over age levels, experiments, and list conditions. In addition, reminiscence, unlike either forgetting or learning, was completely independent of development, and the effects of taxonomic relatedness on reminiscence were always positive.
Model Results
The aim of the model analysis was to pinpoint the process reasons for forgetting and reminiscence, focusing on questions such as: Was forgetting dominated by declines in recollective retrieval or nonrecollective retrieval? Was reminiscence driven by recovery of recollective or nonrecollective retrieval? Were developmental differences in forgetting rates primarily due to differences in recollective or nonrecollective forgetting? Were differences in forgetting rates as functions of cue and target relatedness primarily due to differences in recollective or nonrecollective forgetting?
We report the results in two waves, as before, considering first the question of whether the model, which fit the acquisition data of the first two experiments, also fits the retention data. Then, we estimate the model’s parameters to answer the above questions about the process reasons for forgetting and reminiscence effects.
Fit
We again computed necessity tests followed by sufficiency tests, for each experiment. The full fit results are reported in the Appendix. The overall outcome was the same as before: Thee dual-retrieval model was both necessary and sufficient to account for the data of these experiments.
Parameter Analyses: Process Explanations of Developmental and Treatment Effects in Forgetting
Values of the parameters that measure recollective and nonrecollective retrieval on the retention tests are displayed in Table 5, where values are exhibited separately by experiment, age level, cue relatedness, and target relatedness. As the aim of the experiments was to study forgetting and reminiscence, these values must be considered in relation to parameter values from the acquisition phase (Table 3). That information appears in Table 6, where rates of forgetting have been separately computed for recollective retrieval (FD), reconstructive retrieval (FR), and familiarity judgment (FJ) by experiment, age level, cue relatedness, and target relatedness. The parameter estimates in Table 6 are for the 123 sequence of retention tests. Parameter estimates for the 234 and 345 sequences are not informative because (a) their values depend on the corresponding values for the first tests and (b) those values will be affected by opportunities to reminisce on earlier tests.
Table 5.
Estimates of the Dual-Retrieval Model’s Parameters for Experiments 3 and 4
| Age and relatedness | Recollection
|
Reconstruction
|
Familiarity judgment
|
|||
|---|---|---|---|---|---|---|
| D1f | D2f | R1f | R2f | J1f | J2f | |
|
| ||||||
| Experiment 3 (typical exemplars) | ||||||
| Adolescents: | ||||||
| UU | .71 | .18 | .17 | .00 | .64 | .64 |
| CU | .65 | .07 | .38 | .00 | .52 | .86 |
| UC | .78 | .16 | .61 | .00 | .51 | .66 |
| CC | .54 | .16 | .45 | .28 | .35 | .75 |
| Means | .67 | .14 | .40 | .07 | .52 | .73 |
| Children: | ||||||
| UU | .64 | .14 | .36 | .00 | .44 | .68 |
| CU | .68 | .11 | .32 | .00 | .30 | .69 |
| UC | .74 | .09 | .42 | .00 | .52 | .66 |
| CC | .58 | .06 | .57 | .00 | .34 | .94 |
| Means | .66 | .10 | .42 | .00 | .40 | .75 |
|
| ||||||
| Experiment 4 (atypical exemplars) | ||||||
|
| ||||||
| Adolescents: | ||||||
| UU | .78 | .21 | .22 | .00 | .62 | .37 |
| CU | .76 | .01 | .32 | .00 | .54 | .86 |
| UC | .78 | .21 | .34 | .01 | .50 | .44 |
| CC | .57 | .17 | .11 | .00 | .56 | .23 |
| Means | .71 | .17 | .22 | .00 | .60 | .48 |
| Children: | ||||||
| UU | .59 | .12 | .40 | .00 | .71 | .88 |
| CU | .65 | .08 | .18 | .00 | .62 | .78 |
| UC | .79 | .06 | .50 | .13 | .52 | .75 |
| CC | .40 | .09 | .11 | .00 | .54 | .81 |
| Means | .61 | .09 | .33 | .03 | .58 | .81 |
Table 6.
Estimates of Nonrecollective Retrieval: Learning, Retention, and Forgetting
| Learning
|
Retention
|
Forgetting
|
|||||
|---|---|---|---|---|---|---|---|
| P(R) | J2 | R1f | J1f | FD | FR | FJ | |
|
| |||||||
| Experiment 1 (typical) | |||||||
| Adolescents: | |||||||
| UU | .34 | .44 | .17 | .64 | .29 | .17 | −.20 |
| CU | .30 | .40 | .38 | .52 | .35 | −.08 | −.12 |
| UC | .35 | .46 | .61 | .51 | .22 | −.26 | −.05 |
| CC | .41 | .46 | .45 | .35 | .46 | −.04 | .11 |
| Means | .35 | .44 | .40 | .51 | .34 | −.05 | −.07 |
| Children: | |||||||
| UU | .67 | .40 | .36 | .44 | .36 | .31 | −.04 |
| CU | .32 | .69 | .32 | .30 | .32 | .00 | .39 |
| UC | .74 | .24 | .18 | .42 | .26 | .32 | −.18 |
| CC | .27 | .44 | .57 | .34 | .42 | −.30 | .10 |
| Means | .50 | .44 | .42 | .40 | .34 | .08 | .08 |
|
| |||||||
| Experiment 2 (atypical) | |||||||
|
| |||||||
| Adolescents: | |||||||
| UU | .46 | .35 | .22 | .62 | .22 | .24 | −.27 |
| CU | .63 | .44 | .32 | .54 | .24 | .31 | −.10 |
| UC | .50 | .48 | .34 | .50 | .22 | .24 | −.02 |
| CC | .64 | .72 | .11 | .56 | .43 | .53 | .16 |
| Means | .56 | .50 | .25 | .56 | .28 | .33 | −.06 |
| Children: | |||||||
| UU | .42 | .31 | .40 | .71 | .41 | .02 | −.40 |
| CU | .53 | .28 | .18 | .62 | .35 | .35 | −.34 |
| UC | .55 | .60 | .50 | .52 | .21 | .05 | .08 |
| CC | .46 | .41 | .11 | .54 | .60 | .35 | −.13 |
| Means | .49 | .40 | .33 | .60 | .39 | .19 | −.20 |
Note. P(R) = the proportion of targets that could be reconstructed at the end of learning, J2 = the probability that reconstructed targets would be judged familiarity enough to recall at the end of learning, R1f = the proportion of targets that could be reconstructed by the end of the forgetting interval, J1f = the probability that reconstructed targets would be judged familiarity enough to recall at the end of the forgetting interval, FD = decline in recollective retrieval over the forgetting interval, FR = decline in reconstructive retrieval over the forgetting interval, and FJ = decline in familiarity judgment over the forgetting interval.
Forgetting rates for recollective retrieval, nonrecollective retrieval, and familiarity judgment were computed as follows. It is assumed that items had entered state L by the end of acquisition (cf. footnote 2). Therefore, FD is just 1 − D1f. To compute FR for each age level and condition of each experiment, it was necessary first to compute the proportion of items that subjects had learned how to reconstruct by the end of the acquisition phase [the statistic P(R) in Equation 1]. Those values appear in the first data column of Table 6. Then, FD is P(R) − R1f, where R1f is the probability (from Table 5) that an item can be reconstructed at the end of the forgetting interval. The value of FJ for each age level and condition of each experiment, is simply J2 − J1f, the probability that a reconstructed item is judged to be familiar enough to recall at the end of acquisition minus the probability that a reconstructed item is judged to be familiar enough to recall at the end of the forgetting interval. Thus, the fact that the D, R, and J parameters had different values at the end of the learning does not affect the measurement of their respective forgetting rates. In each case, parameter values are the end of learning (whatever they may be) are used as baselines, against what subsequent forgetting rates are calculated as percent declines from those baselines As all of these parameters values were well above zero, there was ample room for forgetting to occur in all three processes.
Inspection of the forgetting statistics in the last three columns of Table 6 reveals a clear overall pattern: FD > FR > FJ; that is, declines in recollection were more pronounced than declines in reconstruction, which in turn were more marked than declines in familiarity judgment. With respect to recollection and reconstruction, averaging over experiments, age levels, and conditions, the mean probability over the forgetting interval of losing the ability to recollect items was more than twice the probability of losing the ability to reconstruct them (.34 versus .14). As can be seen in Table 6, there was substantial recollective forgetting at both age levels and in all conditions of both experiments, the probabilities of recollective forgetting ranging from a low of .21 to a high of .60. In contrast, the average level of reconstructive forgetting was not above-floor in Experiment 3 (typical materials). Finally, with respect to familiarity judgment, it is apparent from the last data column of Table 6 that there was no forgetting, that reconstructed items were no less likely to be judged familiar enough to recall a week later than at the end of learning. This strongly suggests that whereas recollection and reconstruction are both by-products of learning (because they were subject to forgetting), familiarity judgment is rooted in extra-experimental knowledge (see also, Estes & Maddox, 2002).
Next, consider developmental and treatment variation in forgetting—which, like forgetting, were dominated by recollective declines. In Experiment 3, the ANOVA revealed that cue relatedness had a substantial effect on forgetting, with higher levels for lists with categorized cues than for lists with unrelated cues, and that there was a Cue X Target cross-over, with categorized targets producing more forgetting than unrelated targets when cues were categorized and less when cues were unrelated. Regarding the cue effect, this was a pure recollection effect, the mean probability of recollective forgetting being .39 for pairs with categorized cues versus .28 for pairs with unrelated cues. (The G2(1) test of the null hypothesis that FD was equal for pairs with categorized versus unrelated cues produced a null hypothesis rejection for two of the four comparisons in Table 6.) With respect to the Cue X Target cross-over, this, too, was a pure recollection effect. When cues were categorized, recollective forgetting was greater for pairs with categorized rather than unrelated targets (means = .44 versus .34; both G2(1) tests produced null hypothesis rejections), while recollective forgetting was greater for unrelated than for categorized targets when cues were unrelated (means = .33 versus .24; one of the two G2(1) tests produced a null hypothesis rejection).
Whereas the ANOVA in Experiment 3 revealed taxonomic relatedness effects on forgetting without a developmental effect, the ANOVA in Experiment 4 revealed a developmental effect without taxonomic relatedness effects. Regarding the developmental effect, a glance at the FD column of Table 6 indicates that levels of recollective forgetting were higher in children than in adolescents (means = .39 versus .28). When we computed G2(1) tests that compared the children’s and adolescents’ FD values for each list condition, three of the four conditions (UU, CU, and CC) produced null hypotheses rejections. In addition, inspection of the FR column of Table 6 indicates that reconstructive forgetting was not responsible for the higher level of forgetting in children and that, on the contrary, reconstructive forgetting was higher in adolescents than children (means = .33 versus .19). (Two of the relevant G2(1) tests produced a null hypothesis rejection.) This is an instructive result because it illustrates a key advantage of model-based analysis: Such analyses are able to identify situations in which a developmental difference produced by an ANOVA of a global performance measure is actually the product of processes that exhibit opposite developmental trends.
For convenience, the mean values of the three parametric measures of forgetting are displayed by age level in Figure 2, with the values for Experiment 3 appearing in Panel A and the values for Experiment 4 appearing in Panel B. The process level results for forgetting may be summarized in three simple statements. First, at the end of the forgetting interval, declines in recall were chiefly due to declines in recollective retrieval. Overall, declines in reconstructive retrieval were not reliable in Experiment 3, and declines in familiarity judgment were not reliable in either experiment. Second, developmental differences in forgetting rates, which occurred in Experiment 4 (atypical materials), were wholly due to higher levels of recollective forgetting in children. Third, the effects of taxonomic relatedness on forgetting (Experiment 3) were also pure recollective forgetting differences.
Figure 2.
Developmental trends in forgetting of direct access (parameter F(D)), forgetting of reconstruction (parameter F(R)), and forgetting of familiarity judgment (parameter F(J)) during the long-term retention phase. Experiment 3 (typical exemplars) results appear in Panel A. Experiment 4 (atypical exemplars) results appear in Panel B.
Parameter Analyses: Process Explanations of Developmental and Treatment Effects in Reminiscence
Turning to reminiscence, we have seen that there were strong reminiscence effects at both age levels in all conditions of both experiments. To determine what was responsible for such improvements at the level of process, it is necessary to consider the values of four parameters in Table 5—namely, D2f. R2f, J1f, and J2f,. If D2f > 0, subjects are able to improve recollective retrieval without further study opportunities, which causes recall accuracy to recover. If R2f > 0, subjects are able to improve reconstructive retrieval without further study opportunities, which also causes recall accuracy to recover. Finally, if J2f > J1f, subjects are more likely to judge reconstructed targets to be familiar enough to recall on later tests than on the first test, which also causes recall to recover.
Inspection of the values of these parameters in Table 5 immediately rules out reconstruction as a cause of reminiscence. The mean values of R2f in the two experiments were .04 (Experiment 3) and .02 (Experiment 4), and as can be seen in Table 5, 13 of the 16 estimates of this parameter were 0. Thus, across age levels, experiments, and cue-target manipulations, there was a uniform inability to recover reconstructive retrieval ability without the aid of study opportunities. It might be argued that in Experiment 3, there was nothing to “recover” because, as we saw, there was essentially no reconstructive forgetting in that experiment (the mean value of FR was .02). However, there was ample room for reconstructive recovery in Experiment 4, where the mean value of FR was .26. Yet, there was no evidence of it. The suggestion, then, is that a key element of nonrecollective retrieval, learning how to reconstruct targets from partial information (e.g., features), requires study opportunities.
This leaves recollection and familiarity judgment as potential sources of reminiscence. Concerning recollection, it is clear that it was a major contributor to reminiscence at both age levels in both experiments, the mean values of D2f. being .12 (Experiment 3) and .13 (Experiment 4). (Conceptually, each of these values is the proportion of items that could not be recollected on Test i that could then be recollected on Test i + 1.) In addition, familiarity judgment contributed to reminiscence effects. Specifically, it can be seen in Table 5 that J2f > J1f for children in Experiment 3 (.75 versus .40), for adolescents in Experiment 3 (.73 versus .52), for children in Experiment 4 (.81 versus .58), but not for adolescents in Experiment 4.
When it comes to process explanations of reminiscence, it is important to distinguish between which processes contribute most to absolute levels of reminiscence and which contribute most to treatment effects. With respect to absolute levels of reminiscence, the contributions of recollective retrieval are stronger than the contributions of familiarity judgment in two senses. First, as just noted, J2f was not greater than J1f in adolescents in Experiment 4, and indeed, the opposite was true. Second, increases in D2f contribute more directly to reminiscence than differences between J2f and J1f because familiarity judgment only operates for items that have been reconstructed, and average reconstruction probabilities were well below .50 in both experiments. With respect to treatment effects, on the other hand, familiarity judgment contributed to them. In Experiment 3, it will be remembered that there was a single treatment effect: Reminiscence rates were higher for pairs with categorized cues than for pairs with unrelated cues. Inspection of the values of D2f and J2f in Table 5 shows this to be a pure familiarity judgment effect. Whereas D2f values were virtually the same for the two types of pairs, J2f values were clearly larger for pairs with categorized than with unrelated cues (means = .82 versus .66; three of the four G2 tests producing null hypothesis rejections). In Experiment 4, it will be remembered that there were two treatment effects: Reminiscence rates were higher for pairs with categorized cues than for pairs with unrelated cues and were higher for pairs with categorized targets that for pairs with unrelated targets. It turned out that the process reasons for each effect were different in children than in adolescents—a fact that like the opposite developmental trends in recollective and reconstructive forgetting in Experiment 4, can only be revealed by model-based analyses. In children, both cue and target effects were entirely due to differences in familiarity judgment. In adolescents, the cue effect was due to differences in familiarity judgment, but the target effect was due to differences in the recovery of recollective retrieval.
The mean values of the three parametric measures of reminiscence (D2f, R2f, and J2f − J1f) are displayed by age level in Figure 3, with the values for Experiment 3 appearing in Panel A and the values for Experiment 4 appearing in Panel B. Overall, the model-based analyses converged on the important conclusion that the complementary phenomena of forgetting and reminiscence are symmetrical at the level of retrieval processes. Forgetting was tied primarily to the decline of recollective retrieval over the one-week interval, and reminiscence was tied primarily to the recovery of recollective retrieval over a series of retention tests. However, there were process asymmetries in the age and treatment effects. With respect to forgetting, age and treatment differences in forgetting rates were wholly due to differences in recollective forgetting. With respect to reminiscence, there were no age differences, and treatment differences were primarily due differences in familiarity judgment.
Figure 3.
Developmental trends in reminiscence of direct access (D = D2f), reminiscence of reconstruction (R = R2f), and reminiscence of familiarity judgment (J = J2f −J1f) across the sequence of retention tests. Experiment 3 (typical exemplars) results appear in Panel A. Experiment 4 (atypical exemplars) results appear in Panel B.
General Discussion
The research reported in this paper is perhaps best viewed as a proof of concept, the concept being whether it is possible to evaluate theoretical hypotheses about the contributions of recollective and nonrecollective retrieval to the development of learning, forgetting, and reminiscence with a low-burden recall technique. The motivation for this approach arises from the fact that the dual-process literature contains theoretical proposals about subject groups whose cognitive limitations place obstacles in the path of traditional metacognitive measures. Those subject groups include, most notably, the standard child and young adolescent populations of developmental research and older adult populations with neurocognitive impairments. It is well established that even young children and older adults with severe impairments (e.g., Alzheimer’s or Parkinson’s dementia) are capable of performing recall tasks on which they participate in a few study-test trials on a focal list, and that their recall improves across such trials. We investigated a very low-burden version of such tasks, in which subjects participate in only three trials on a focal list. Despite the simplicity of this procedure, the resulting data space is sufficiently rich that it is possible to conduct fit tests for both two-process and one-process models and to obtain two separate measures of recollective retrieval, reconstructive retrieval, and familiarity judgment (Table 1).
To evaluate this procedure, we focused on normal developmental populations, a classic form of recall (associative recall), and list manipulations that exhibit strong age variability (taxonomic relatedness). The procedure was used to measure developmental trends in recollective and nonrecollective retrieval and to measure developmental trends in the effects of taxonomic relatedness. This was done in the domain in which dual-retrieval operations have ordinarily been studied—namely, as episodic memories are first acquired during list presentations. To broaden the procedure’s scope, we extended it to a domain in which dual-retrieval operations have infrequently been studied (forgetting), and to a domain in which, as far as we know, they have never been studied (reminiscence). A general finding was that this low-burden technique is a promising method of investigating dual-retrieval operations in all three spheres. Here, fit tests at both age levels, for all combinations of cue and target relatedness, showed that (a) the data were never successfully fit by a model that assumed that recall involves a single nonrecollective retrieval operation or a single recollective retrieval operation and that (b) the data were always successfully fit by a model that assumes that recall involves a recollective operation, plus a reconstructive operation that is accompanied by familiarity judgments. In the remainder of this section, we discuss what the dual-retrieval analysis revealed about developmental trends in learning, forgetting, and reminiscence and about the effects of taxonomic relatedness on learning, forgetting, and reminiscence.
Developmental Trends in Dual-Retrieval Processes
One extant hypothesis posits that developmental improvements in episodic memory are consequences of improvements in recollective retrieval because the development of familiarity is largely complete by the end of early childhood (Ghetti & Angelini, 2008). A second hypothesis (Brainerd et al., 2009) posits that improvements in episodic memory are due to improvements in both recollective and nonrecollective retrieval because (a) familiarity continues to develop through young adulthood and (b) familiarity is only one component of nonrecollective retrieval (the other being reconstruction). The second hypothesis also stresses that relative rates of developmental change in dual-retrieval processes are different during different age ranges and for memory tasks (which motivated the inclusion of the typicality manipulation in our experiments). A key reason for the differing claims of the two hypotheses is methodological; that the first was formulated with reference to the customary recognition approach to dual-retrieval processes, which does not encompass reconstructive retrieval, while the second was formulated with reference to the newer recall approach.
Both hypotheses share the limitation that their predictions have been confined to the domain in which dual-retrieval operations have traditionally been studied: performance when subjects first learn to remember items on lists. Neither hypothesis makes explicit predictions about how dual-retrieval processes contribute to developmental changes in two other core domains of episodic memory, forgetting and reminiscence. However, if we extrapolate the first hypothesis to these domains, the likely prediction is that developmental changes in forgetting and reminiscence would be controlled by recollection. Note that this is consistent with the standard idea from the adult literature that forgetting is largely synonymous with declines in recollection (Barber, Rajaram, & Marsh, 2008; Gardiner & Java, 1991; Sharot & Yonelinas, 2008; Viskontas, Carr, Engel, & Knowlton, 2009; Tunney, 2010). On the other hand, if we extrapolate the second hypothesis, the likely prediction is that recollective and nonrecollective retrieval would both contribute to developmental changes in forgetting and reminiscence.
What did the data show? Consider, first, the overall picture for learning. Here, the results of Experiment 1, in which lists were composed of very familiar words (e.g., coat, horse), seemed to support the first hypothesis. Between childhood and early adolescence, associative recall improved substantially and the values of recollection parameters increased substantially as well, while the values of the reconstructive and familiarity judgment parameters did not. However, that support vanished in the second experiment, in which lists were composed of less familiar words (e.g., blouse, moose). Now, the data were consistent with the second hypothesis. Between childhood and early adolescence, associative recall improved substantially and so did the values of the reconstruction and familiarity judgment parameters. Moreover, the quantitative details of the relative contributions of recollective and nonrecollective retrieval were the reverse of the first experiment. More explicitly, over the various list conditions, the average age increase in the two recollection parameters was small and not reliable in most conditions, but the average increase in one of the two recollection parameters was large (R2 more than doubled overall) and the two familiarity judgment parameters increased by more than 50%.
Beyond providing differential support for one of the two hypotheses, the learning data suggest that the picture of relative developmental change in dual-retrieval operations is dramatically influenced by whether or not episodic memory tasks focus only on very familiar materials. Although that may seem a trivial point, it is of considerable significance from the perspective of the memory development literature. In that literature, to ensure above-floor performance at younger age levels, it is standard practice to administer recall and recognition tasks in which to-be-remembered items consist of only very familiar words, objects, and events. This, it now seems, may bias our conclusions about the relative contributions of nonrecollective retrieval to episodic memory development.
What did the data show about forgetting? Generally speaking, the picture did not favor the predictions that were extrapolated from either hypothesis. To begin, it should be noted that levels of forgetting were substantial at both age levels in both experiments, averaging above 30%. Next, two important null findings should be noted. First, there was no evidence of forgetting of familiarity judgment, at either age level, regardless of material or list condition. Second, unlike learning, developmental differences in forgetting were restricted to atypical materials. Moreover, inspection of the average values of the recollective and reconstructive forgetting parameters for typical materials (Table 6) reveals that the values were virtually identical for children and adolescents. On the positive side, there were developmental declines in forgetting with atypical words, and with such materials, there was substantial age variability in both recollective and reconstructive forgetting, as would be anticipated on the basis of the second hypothesis. However, the age changes in recollection and reconstruction were in opposite directions: The recollective forgetting parameter D1f decreased substantially with age, but the reconstructive forgetting parameter R1f increased substantially. Neither of the preceding hypotheses provides a mechanism for explaining such an Age X Retrieval Process cross-over.
Finally, concerning reminiscence, the developmental picture was simple: There was none. Reminiscence rates did not vary with age for either typical or atypical materials. Because reminiscence involves recovering the ability to recall targets over a series of tests, without further opportunities to study lists, a natural possibility is low power; that reminiscence rates were too low to have a good chance of detecting developmental changes. That explanation fails, however, because reminiscence rates between the first and last retention test were sizeable, averaging 18% with typical words and 13% with atypical words. Further, it is not that reminiscence is simply impervious to the influence of design variables because, on the contrary, it varied as a function of the taxonomic relatedness of both cues and targets.
We conclude with some general observations about the degree of support for the aforementioned hypotheses. In the learning domain, the data were consistent with the predictions of the second hypothesis. Recollection, reconstruction, and familiarity judgment all contributed to developmental improvements in recall, with their respective contributions varying as a function of whether materials were typical or atypical. In the forgetting domain, the data were not congenial to either hypothesis. Developmental differences in forgetting were restricted to atypical materials, and although recollective and reconstructive forgetting both varied with age, they varied in opposite directions. In the reminiscence domain, there was no age variability to explain, for either typical or atypical materials.
Developmental Trends in Taxonomic Relatedness
It has long been understood that taxonomic relatedness influences the accuracy of adults’ recall, enhancing it the case of free recall (Mandler, 1967) and impairing it in the case of associative recall (Underwood et al., 1965). We included this manipulation in our experiments, for two reasons. First, a dual-retrieval explanation of its effects has been previously worked out for adults by applying the present modeling approach to free and associative recall data (Brainerd & Reyna, 2010). A key finding of that research was that although taxonomic relatedness has opposite effects on accuracy in the two paradigms, its process-level effects are qualitatively similar: Relative to unrelated words, taxonomically-related ones make recollection harder but reconstruction and familiarity judgment easier, with the manipulation’s opposite effects on accuracy being due to the fact that its recollective effects are more pronounced than its reconstruction/familiarity effects in associative recall but less pronounced in free recall. Second, the effects of semantic relatedness on accuracy are known to increase throughout childhood and adolescence, in a variety of tasks (e.g., see Brainerd, Reyna, & Ceci, 2008; Reyna & Rivers, 2008). The usual theoretical interpretation is that semantic organization of episodic memory develops gradually between early childhood and young adulthood. By applying the present modeling approach to the data of different age levels, it is possible to track the changing effects of taxonomic relatedness on recollection, reconstruction, and familiarity judgment, as semantic organization develops. Those trends can then be interpreted, using the established adult pattern as a baseline.
The developmental data revealed quantitative and qualitative changes, relative to adults, at the level of raw recall and at the level of retrieval processes. With respect to raw recall, in adults, taxonomic relatedness impairs associative recall when it is manipulated on either the cue or target sides of pairs, and the effects on the cue side are larger. Not so with children and adolescents. With typical materials, adolescents, like adults, displayed interference effects on both the cue and target sides, but there was a quantitative difference because the two effects were of similar magnitude (whereas the cue effect is larger in adults). Children were qualitatively different than adults. Although they displayed the adult interference pattern on the target side, categorized cues actually improved their recall when targets were unrelated. Thus, taxonomic interference was stronger on the target side for children, so that the child-to-adult developmental trend with typical materials is: stronger target interference (children) → equivalent cue-target interference (young adolescents) → stronger cue interference (young adults). With atypical materials, there were qualitative differences between the adolescent and adult patterns, as well as between the child and adult patterns, and most importantly, taxonomic relatedness sometimes enhanced adolescents’ as well as children’s recall. In adolescents, taxonomic relatedness on the cue side always impaired recall (as with typical materials) but on the target side, it enhanced recall when cues were related, though it impaired recall when cues were unrelated (as with typical materials). In children, there were no interference effects at all. Taxonomic relatedness always improved recall on the target side, and it had no effect on the cue side.
Summing up, the adult pattern, in which lists that activate taxonomic relations among words make associative recall harder, requires many years to emerge. The basic elements of this pattern can be detected by early adolescence when lists consist of very familiar words, but it breaks down on the target side when words are less familiar. The pattern cannot be detected at all in children, regardless of words’ familiarity. Indeed, taxonomic relatedness mostly helped children’s recall, on the cue side when words were very familiar and on the target side when they were not.
In the modeling analyses of Experiments 1 and 2, specific developmental trends in dual-retrieval processes were reported that explained specific age changes in how taxonomic relatedness affected recall accuracy. Here, however, we focus attention on global trends in how taxonomic relatedness affects recollective and nonrecollective retrieval. In adults, as mentioned, taxonomic relatedness impairs the former and enhances the latter on both the cue and target sides, with the net reduction in accuracy being due to the fact that recollective impairment is a larger effect than nonrecollective enhancement (Brainerd & Reyna, 2010). A glance at the parametric results in Table 3 indicates that these process-level effects are slow to develop. Taking recollection first, this retrieval process provides the clearest evidence that one element of the adult pattern has emerged by early adolescence. Specifically, when either the cue or target side was categorized, the overall means of the D1 and D2 parameters were reduced, for both typical and atypical items. Thus, the adult tendency for recollection to be harder when cues or targets activate taxonomic relations is clearly present by early adolescence. Just as clearly, there was no evidence of this tendency a few years earlier: In Table 3, the overall means of the D1 and D2 parameters were simply not affected by this manipulation, with the average parameter difference between conditions that differed in cue or target relatedness being only .03. Turning to nonrecollective retrieval, we saw that there were specific age differences in reconstruction and familiarity judgment that explained specific age differences in taxonomic relatedness effects. However, the overall developmental picture in Table 3 is that taxonomic relatedness did not affect reconstruction or familiarity judgment in a consistent manner at either age level. Pooling over typical and atypical materials, the overall means of the reconstruction parameters were slightly lower for related than for unrelated words (a .07 difference at both age levels), while the overall means of the familiarity judgment parameters were slightly higher for related than for unrelated words (a .09 difference in adolescents versus a .07 difference in children). In short, the general developmental picture from the first two experiments is that one element of the adult pattern, in which taxonomic relatedness hampers recollective retrieval, emerges between childhood and adolescence, whereas the other element, in which taxonomic relatedness facilitates nonrecollective retrieval, emerges between early adolescence and young adulthood.
In contrast to the learning domain, there is no established adult pattern of how taxonomic relatedness affects dual-retrieval processes in the forgetting domain or in the reminiscence domain. Hence, we can only note the overall trends that were observed between childhood and adolescence. Concerning forgetting, remember, first, that forgetting was confined to recollection and reconstruction because there was no evidence of declines in familiarity judgment among either children or adolescents. There was a developmental change in how recollective forgetting was influenced by taxonomic relatedness, with the tendency of related items to increase recollective forgetting being more marked in young adolescents than in children. However, the effects of taxonomic relatedness on reconstructive forgetting, which only occurred in Experiment 2, did not vary with age. Concerning reminiscence, we saw that reminiscence rates did not vary with age, and neither did the process-level effects of taxonomic relatedness. In both Experiment 3 and Experiment 4, recovery of recollective retrieval ability was enhanced when words were related at both age levels. Further, in Experiment 4, increases in familiarity judgment over retention tests were enhanced when words were related at both age levels. Thus, the developmental invariance picture for reminiscence held at level of retrieval processes as well as at the level of raw recall.
Concluding Comments: Forgetting and Reminiscence in the Era of Dual Processes
It will not have escaped readers’ attention that an appealing feature of the recall approach to dual processes is that it supplies a unified technology for comparing recollective and nonrecollective retrieval in the learning, forgetting, and reminiscence spheres. The model delivered good accounts of the data of long-term retention tests, as well as the data of learning trials, allowing its parameters to be used to measure the contributions of recollection, reconstruction, and familiarity judgment in all three domains. As the present experiments are the first to exploit this capability, our findings about differential contributions in the different domains are necessarily tentative. Nonetheless, two overriding patterns are worthy of mention, if only to identify them as prime targets for future experimentation. First, while nonrecollective retrieval contributed substantially to learning in all conditions at both age levels, forgetting was chiefly a recollective phenomenon. Forgetting was entirely recollective in Experiment 3, and substantially so in Experiment 4. Second, likewise, reminiscence was primarily a recollective phenomenon. Whereas estimates of D2f showed that recollective retrieval recovered over retention tests, estimates of R2f showed that reconstructive retrieval did not recover.
To motivate future research, it should be noted that the recollective dominance of forgetting and reminiscence might be contingent on the use of associative recall. As mentioned, it has previously been found that initial learning is more strongly influenced by recollection in associative recall than in free recall (Brainerd & Reyna, 2010). This may be responsible for the present findings, and hence, nonrecollective processes could make larger contributions to forgetting and reminiscence in free recall designs. For reminiscence in particular, another factor that points in the same direction is that associative recall tests can be thought of as “partial study trials” inasmuch as the cue member of each study pair is represented. This feature of the present retention tests could provide differential support for recollection-based reminiscence—as compared to free recall tests, in which none of the studied material is represented.
When it comes to testing theoretical hypotheses about relations between learning, forgetting, and reminiscence, the dual-retrieval model has a pair of useful strategic properties. The first is that it allows recollective and nonrecollective forgetting to be expressed as functions of these processes’ initial levels of learning, by providing separate estimates of each process (a) at the end of learning and (b) at the end of a forgetting interval. The model’s other strategic property is that when dual-retrieval processes are measured after a forgetting interval, forgetting of recollective and nonrecollective retrieval are not confounded with reminiscence of these processes. The model provides separate estimates of recollection, reconstruction, and familiarity judgment before and after reminiscence has operated. Consequently, when a subject or treatment variable is found to affect forgetting of these processes, it is not because that variable affects reminiscence instead.
Finally, it will also not have escaped readers’ attention that a possible alternative to our measurement approach would be to administer one of the traditional metacognitive judgment tasks in conjunction with recall paradigms. Indeed, this was recently done by McCabe, Roediger, and Karpicke (2011), who used both inclusion/exclusion tasks and remember/know tasks to measure dual-retrieval processes in free recall. Consistent with our results, McCabe et al. concluded that free recall involves a nonrecollective process as well as a recollective one and that a manipulation that has often been used to separate the two processes in recognition (full versus divided attention) is able to separate them in free recall. On the positive side, because the focal memory task is recall, McCabe et al.’s approach avoids the first challenge to metacognitive tasks that was discussed earlier—namely, that recognition may involve only a single retrieval process. On the negative side, this approach does not resolve the second challenge—namely, the validity criticisms of individual metacognitive tasks. Further, administering such tasks with recall resurrects the problem of high-burden measurement and reintroduces the obstacles to measuring dual-retrieval processes in normal developmental populations and in adults with neurocognitive impairments.
Highlights.
We measured recollective and nonrecollective retrieval with a very low-burden recall model.
The model measures both retrieval processes in learning, forgetting, and reminiscence.
Recollective and nonrecollective retrieval both affected the development of episodic memory.
Acknowledgments
Portions of the research were supported by grants from the Natural Sciences and Engineering Research Council to the first author and by National Institutes of Health Grant 1RC1AG036915-01 to both authors. The software that was used to conduct the analyses of the dual-retrieval model that are reported in this paper (goodness-of-fit tests, parameter estimation, and significance tests of parameter values) is available from the first author upon request. This modeling program, which runs on any Windows-based PC, is easy to use in clinical as well as experimental applications. The minimum data requirement is three recall tests per list item. With such data, one merely counts the number of instances of each of the possible response sequences (CCC, CCE, …, EEE) and inputs those counts to the program, which then returns parameter values and fit tests). A spreadsheet program is also available from the author that will perform these counts automatically.
Appendix
Dual-Retrieval Model
Consider a simple experiment of the form S1T1S2T2, S3T3; that is, there are three study cycles on the target list, with a recall test following each study cycle. As there are three separate recall tests, each item on the list can exhibit one of 8 different patterns of successes and errors over these tests: C1C2C3C4, C1C2C3, C1E2C3, …, E1E2E3, where Ci indicates that the item was recalled on the ith test and Ei indicates that it was not recalled. All of the model’s parameters in Table 1 can be estimated for any set of such data by (a) expressing the observed probability of each of the 8 error-success patterns in a two-stage Markov process that contains the parameters. The states of the process are U (an initial no-recall state), P (an intermediate partial-recall state, with a correct recall substate PC and an incorrect recall substate PE, in which the probability of successful recall has some average value 0 < p < 1), and L, a terminal criterion-recall state. The two-stage Markov process for these states consists of a starting vector W1 and a transition matrix M:
| (A1) |
The probabilities of the 8 individual error-success patterns are obtained by simply multiplying the vector and the matrix together. Those expressions are
| (A2) |
| (A3) |
| (A4) |
| (A5) |
| (A6) |
| (A7) |
| (A8) |
| (A9) |
The likelihood of any sample of data (and estimates of the parameters in Table 1) is then obtained by maximizing the following likelihood function:
| (A10) |
The pi are the 8 expressions on the right sides of Equations A2– A9, and because the terms in Equation A10 are multiplied, this expression can only be maximized if all the pi > 0, which means that all the exponents must be > 0: Because the exponent of each pi is an empirical data count that corresponds to one of the 8 error-success sequences (i.e., the exponent is merely the number of times that error-success sequence was observed in sample data), pi can only be greater than 0 if N(i) is greater than 0. Because 6 memory parameters are estimated, the likelihood value in A10 is computed with 1 degree of freedom. A goodness-of-fit test that evaluates the null hypothesis that no more than two retrieval processes are required to account for the data is then obtained by computing a likelihood ratio statistic that compares the likelihood in A10 to the likelihood of the same data when all 7 observable probabilities are free to vary. That test statistic, which is asymptotically distributed as χ2(1), is
| (A11) |
where L7 is the likelihood of the data when all 7 observable probabilities are free to vary.
By imposing parameter restrictions on Equation A11, this same test statistic is used to evaluate within- and between-condition hypotheses about differences in parameter values, as follows. Taking the between-condition tests first, consider an experiment that contains k different conditions. To test hypotheses about whether some specific parameter (say, D1) differs between a pair of conditions, two steps are involved: (a) An experimentwise test is computed that determines whether there is global statistical evidence that the target parameter differs among the k conditions, and (b) if the experimentwise test yields a null hypothesis rejection, condition wise tests are computed to determine whether the target parameter differs between specific pairs of conditions. The first test statistic is
| (A11a) |
where the denominator contains the values of the numerator of Equation A11 that are computed for the data of each of the k conditions, the numerator contains a single value of the numerator of Equation A11 that is computed for the pooled data of the k conditions under the constraint that the value of the target parameter is the same in all conditions, and the G2 statistic is asymptotically distributed as χ2(2k). The second test statistic, for two conditions i and j is
| (A11b) |
which is asymptotically distributed as χ2(2). The numerator is a single value of the numerator of Equation A11 that is computed for the pooled data of the two conditions under the constraint that the value of the target parameter is the same in those conditions, and the denominator is the two likelihood values from the denominator of Equation 11a for these two conditions.
Turning to within condition-parameter tests, these tests compare the values of different parameter pairs (say, D1 versus D2) within a single condition. Such a test stipulates that a numerical relation of equality or inequality holds between the members of the pair. The test statistic is just
| (A11c) |
which is asymptotically distributed as χ2(2) because the likelihood in the numerator is estimated with one less degree of freedom than when all six parameters are free to vary.
One-Process Models
A second goodness-of-fit test can be computed that evaluates the null hypothesis that learning to recall involves only a single nonrecollective process. This one-process model is obtained from the two-process model by merely eliminating one of the Markov states:
| (A12) |
The likelihood of any set of data over which A11 can be defined can also be estimated for the one-process model in A12 by maximizing a simplified version of A11 that contains only the parameters in A12. The revised fit statistic is then
| (A13) |
which is asymptotically distributed as χ2(3) because the one-process model contains only four memory parameters.
Another goodness-of-fit test of a one-process model can be computed, which assumes that the process is recollective rather than nonrecollective retrieval. The recollective one-process model is also obtained from the two-process model by merely eliminating one of the Markov states, as follows:
| (A14) |
The likelihood of any set of data over which A11 can be defined can also be estimated for this one-process model maximizing a simplified version of A11 that contains only the parameters in A12. The revised fit statistic is then
| (A15) |
which is asymptotically distributed as χ2(5) because this one-process model contains only two memory parameters.
Note that if the fit statistic in A13 produces a null hypothesis rejection (showing that recall involves more than a single nonrecollective process), it is unnecessary to then compute the fit test in A15 (to determine whether recall involves a single recollective process) because the recollective one-process model in A14 is a submodel of the nonrecollective one-process model in A12.
Fit Results: Experiments 1 and 2
The first one-process model, which assumes that recall is based on a single nonrecollective retrieval operation, is shown in Equation A12. The fit test for this model (Equation A13) produces a G2 statistic with 3 degrees of freedom for each experimental condition. G2 is asymptotically distributed as χ2(Riefer & Batchleder, 1988), so the critical value of the statistic to reject the null hypothesis of fit at the .05 level for a single experimental condition is 7.82. In principle, this test, as well as the fit tests for the other one-process model and for the two-process model, can be computed at either the group level (by aggregating data over subjects) or at the individual level. The lengths of the lists that were administered in these experiments were too short to generate enough data points per subject to fit models at the individual level, so all fits were at the group level.
In each experiment, there were a total of 8 conditions (2 age levels × 2 cue conditions × 2 target conditions), so the experimentwise test of model fit for Equation A12 (which controls α at .05) has 24 degrees of freedom and a critical value of 36.42 to reject the null hypothesis. Actually, because the present models are defined over sequences of three study-test trials and the design included two recall tests after the first study cycle, this fit test can be computed in two ways—namely, for the data of recall tests 1A, 2, and 3, and for the data of recall tests 1B, 2, and 3. The baseline model is the same for both sequences, although parameter estimates may be different. In both experiments, both sequences produced values of the test statistic that exceeded the critical value by wide margins (all ps < .0001), those values being roughly 10 times the critical value. Hence, a model that posits only a single nonrecollective retrieval process could not handle the data of either experiment. Those data also could not be fit by a model that posits only a single recollective retrieval process, which is shown in Equation 14A. As we indicated there, if the fit test for the nonrecollective one-process model (Equation A13) produces a null hypothesis rejection, the fit test for the recollective one-process model (Equation A15) must do likewise.
With respect to whether the dual-retrieval model is sufficient to account for the data, the fit test for this model (see Equation A11) produces a G2 statistic with 1 degree of freedom for each experimental condition. Thus, the critical value of this statistic to reject the null hypothesis at the .05 level for a single experimental condition is 3.84, and the critical value for the experiment wise test of the null hypothesis is 15.51. As above, there are two sequences of study-test trials for which this statistic can be computed (1A,-2-3 and 1B-2-3). The null hypothesis of model fit was not rejected in any of the tests, and indeed, none of the statistics even approached the critical value. The values of the individual test statistics were 11.68 and 11.97 for Experiment 1 and 9.19 and 7.54 for Experiment 2. Thus, across the two experiments, the average value of the test statistic for the dual-retrieval model was well below the critical value to reject the null hypothesis of fit, whereas the average values of the corresponding test statistics for the one-process models were far above the critical values. Therefore, the dual-retrieval model was both necessary and sufficient to account for the data.
Fit Results: Experiments 3 and 4
As before, the necessity test for each condition of each experiment was a G2 statistic with 3 degrees of freedom, while the sufficiency test was a G2 statistic with 1 degree of freedom. As we just saw, because the present models are defined over sequences of three consecutive study-test trials, multiple fit tests can be conducted for any condition—one for each sequence of three consecutive trials. Subjects responded to a total of five retention tests, so that there were three such sequences for any condition (T1T2T3, T2T3T4, T3T4T5). In each experiment, there were 8 distinct conditions (2 age levels × 4 list conditions), so that the critical value for the experiment wise G2(3) fit test to reject the null hypothesis that the one-process model fits the data is 36.42. As just mentioned, three such experiment wise tests were possible, one for each three-test sequence, for a total of six tests in all. We computed all these tests, and they all exceeded the critical value by wide margins (all ps < .0001). Therefore, the retention data, like the acquisition data, could not be fit by a model that assumes that associative recall consists of a single non recollective retrieval process or a model that assumes that recall consists of a single recollective retrieval process.
Turning to the sufficiency tests, these tests again evaluated the null hypothesis that associative recall is not more complex than the dual-retrieval model supposes and that, therefore, such data are well fit by that model. For each condition, the relevant test produces a G2 statistic with 1 degree of freedom. Thus, the critical value to reject the null hypothesis at the .05 level for a single condition is 3.84, and the critical value for the experiment wise test of the null hypothesis is 15.51. As there are three sequences of retention tests for which this statistic can be computed, there was one such test for each sequence, for each age level in each experiment. The null hypothesis of model fit was not rejected in any of the tests. In Experiment 3, the mean value of the test statistics was 13.91, and in Experiment 4, the corresponding mean value was 14.61.3 Therefore, the dual-retrieval model was both necessary and sufficient to account for the retention data, as was for the learning data.
Footnotes
The absorption property of L holds only as long as learning trials continue. Once learning is complete, the absorption constraint is relaxed, and items that have reached L can fall back to P or L as time passes. This feature allows forgetting and reminiscence to be modeled with the same two-stage Markov chains as learning (see Experiments 3 and 4). In that same vein, note that an item can reach L in two distinct ways, by transitioning directly from U to L or by first transitioning from U to P and then transitioning from P to L on some subsequent trial, which means that subjects learn to directly access some items without first learning to reconstruct them but learn to directly access other items after learning to reconstruct them. This is another key feature of the present model because it allows the recollective and nonrecollective components of forgetting and reminiscence to be separated from each other (see Experiments 3 and 4).
Under the dual-retrieval model, there is a small residual probability that an item has not yet entered L, no matter how many consecutive errorless recall tests comprise the acquisition criterion. However, this probability can be calculated exactly for any condition, using estimates of the D, R, and J parameters for that condition. It could be calculated for the subjects in Experiments 3 and 4 because they had participated in Experiments 1 and 2, and hence, estimates of these parameters were available. When we calculated this probability for the various conditions of Experiments 1 and 2, all of the values were < .02. Therefore, this issue was ignored in our report of the forgetting results.
Rather than define the model over each of three consecutive triads of retention tests (123, 234, and 345) and then compute fit tests and estimate parameters for each triad, it is a simple matter, mathematically, to define it over the full sequence of five retention tests. In principle, that would allow computation of a single fit test and estimation of a single set of parameter values for each Age X Condition cell of each experiment. Although that would have been a more elegant procedure, it could not be implemented owing to a technical mathematical obstacle—namely, a zero-outcome problem for the five-trial data space. That space consists of 32 distinct error-success patterns (i.e., CCCCC, CCCCE, CCCEC, …, EEEEE). Unless the number of Subjects X Items per condition in an experiment is quite large (say, > 1,500), it is inevitable, statistically, that the number of data points for some of these error-success patterns will be zero, which means that the corresponding pi term in the model’s likelihood function will be 0. The model cannot be applied when some of the pi = 0 because, as discussed in the Appendix, its likelihood function can only be maximized when all pi > 0. In Experiments 3 and 4, we found that when the model was defined over the full sequence of five retention tests, the number of data points per error-success pattern in the various Age X Condition cells was 0, on average, for more than one-third of the patterns. In contrast, the zero-outcome problem never arose when the model was defined over the three triads of consecutive trials. Therefore, that definition was used in Experiments 3 and 4.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Anderson JR, Bower GH. Recognition and retrieval processes in free recall. Psychological Review. 1972;79:97–123. doi: 10.1037/h0033773. [DOI] [Google Scholar]
- Barber SJ, Rajaram S, Marsh EJ. Fact learning: How information accuracy, delay, and repeated testing change retention and retrieval experience. Memory. 2008;16:934–946. doi: 10.1080/09658210802360603. [DOI] [PubMed] [Google Scholar]
- Battig WF, Montague WE. Category norms for verbal items in 56 categories: A replication and extension of the Connecticut category norms. Journal of Experimental Psychology Monograph. 1969;80(3 Pt 2) doi: 10.1037/h0027577. [DOI] [Google Scholar]
- Billingsley RL, Smith LM, McAndrews PT. Developmental patterns in priming and familiarity in explicit recollection. Journal of Experimental Child Psychology. 2002;82:251–277. doi: 10.1016/S0022–0965(02)00007–3. [DOI] [PubMed] [Google Scholar]
- Bjorklund DF. How changes in knowledge base contribute to the development of children’s memory. Developmental Review. 1987;7:93–130. doi: 10.1016/0273–2297(87)90007–4. [DOI] [Google Scholar]
- Bjorklund DF. Children’s thinking: Developmental and individual differences. 4. Pacific Grove, CA: Wadsworth; 2004. [Google Scholar]
- Bjorklund DF, Muir JE. Annals of Child Development. Vol. 5. Greenwich, CT: JAI Press; 1988. Children’s development of free recall memory: Remembering on their own; pp. 79–123. [Google Scholar]
- Bower GH, Theios JA. A learning model for discrete performance levels. In: Atkinson RC, editor. Studies in mathematical psychology. Stanford, CA: Stanford University Press; 1964. [Google Scholar]
- Brainerd CJ, Howe ML, Desrochers A. The general theory of two-stage learning: A mathematical review with illustrations from memory development. Psychological Bulletin. 1982;91:634–665. doi: 10.1037/0033–2909.91.3.634. [DOI] [Google Scholar]
- Brainerd CJ, Payne DG, Wright R, Reyna VF. Phantom recall. Journal of Memory and Language. 2003;48:445–467. doi: 10.1016/S0749–596X(02)00501–6. [DOI] [Google Scholar]
- Brainerd CJ, Reyna VF. Memory independence and memory interference in cognitive development. Psychological Review. 1993;100:42– 67. doi: 10.1037/0033–295X.100.1.42. [DOI] [PubMed] [Google Scholar]
- Brainerd CJ, Reyna VF. The science of false memory. New York: Oxford University Press; 2005. [Google Scholar]
- Brainerd CJ, Reyna VF. Recollective and nonrecollective recall. Journal of Memory and Language. 2010;63:425–445. doi: 10.1016/j.jml.2010.05.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brainerd CJ, Reyna VF, Ceci SJ. Developmental reversals in false memory: A review of data and theory. Psychological Bulletin. 2008;134:343–382. doi: 10.1037/0033–2909.134.3.343. [DOI] [PubMed] [Google Scholar]
- Brainerd CJ, Reyna VF, Howe ML. Trichotomous processes in early memory development, aging, and neurocognitive impairment: A unified theory. Psychological Review. 2009;116:783–732. doi: 10.1037/a0016963. [DOI] [PubMed] [Google Scholar]
- Brainerd CJ, Reyna VF, Howe ML, Kingma J. The development of forgetting and reminiscence. Monographs of the Society for Research in Child Development. 1990;53:3–4. v-93. doi: 10.2307/1166106. [DOI] [PubMed] [Google Scholar]
- Brown R, McNeill D. The “tip of the tongue” phenomenon. Journal of Verbal Learning and Verbal Behavior. 1966;5:325–337. doi: 10.1016/S0022–5371(66)80040–3. [DOI] [Google Scholar]
- Bugaiska A, Morson S, Moulin CJA, Souchay C. Metamemory, recollection and familiarity in Alzheimer’s disease. Revue Neurologique. 2011;167:3–13. doi: 10.1016/j.neurol.2010.03.001. [DOI] [Google Scholar]
- Donaldson W. The role of decision processes in remembering and knowing. Memory & Cognition. 1996;24:523–533. doi: 10.3758/BF03200940. [DOI] [PubMed] [Google Scholar]
- Dunn JC. Remember-know: A matter of confidence. Psychological Review. 2004;111:524–542. doi: 10.1037/0033–295X.111.2.524. [DOI] [PubMed] [Google Scholar]
- Dunn JC. The dimensionality of the remember–know task: A state-trace analysis. Psychological Review. 2008;115:426–446. doi: 10.1037/0033–295X.115.2.426. [DOI] [PubMed] [Google Scholar]
- Estes WK, Maddox WT. On the processes underlying stimulus-familiarity effects in recognition of words and nonwords. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2002;28:1003–1018. doi: 10.1037/0278–7393.28.6.1003. [DOI] [PubMed] [Google Scholar]
- Gardiner JJ, Java RI. Forgetting in recognition memory with and without recollective experience. Memory & Cognition. 1991;19:617–623. doi: 10.3758/BF03197157. [DOI] [PubMed] [Google Scholar]
- Ghetti S. Processes underlying developmental reversals in false memory formation: Comment on Brainerd, Reyna, and Ceci (2008) Psychological Bulletin. 2008;134:764–767. doi: 10.1037/0033–2909.134.5.764. [DOI] [PubMed] [Google Scholar]
- Ghetti S, Angelini L. The development of recollection and familiarity in childhood and adolescence: Evidence from the dual process signal detection model. Child Development. 2008;79:339–358. doi: 10.1111/j.1467–8624.2007.01129.x. [DOI] [PubMed] [Google Scholar]
- Gomes CFA, Stein LM, Brainerd CJ. Emotional recall: A dual-trace analysis. Paper presented at Psychonomic Society; Seattle, WA. 2011. Nov, [Google Scholar]
- Glanzer M, Kim K, Hilford A, Adams JK. Slope of the receiver-operating characteristic in recognition memory. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1999;25:500–513. doi: 10.1037/0278–7393.25.2.500. [DOI] [Google Scholar]
- Greeno JG. Identifiability and statistical properties of two-stage learning with no successes in the initial stage. Psychometrika. 1968;33:173–215. doi: 10.1007/BF02290152. [DOI] [PubMed] [Google Scholar]
- Greeno JG. Representation of learning as discrete transition in a finite state space. In: Krantz DH, Atkinson RC, Luce RD, Suppes P, editors. Contemporary developments in mathematical psychology. San Francisco, Calif: Freeman; 1974. [Google Scholar]
- Greeno JG, James CT, DaPolito FJ. A cognitive interpretation of negative transfer and forgetting of paired associates. Journal of Verbal Learning and Verbal Behavior, 1971. 1971;10:331–345. doi: 10.1016/S0022–5371(71)80032–4. [DOI] [Google Scholar]
- Hicks JL, Marsh RL. On predicting the future states of awareness for recognition of unrecallable items. Memory & Cognition. 2002;30:60–66. doi: 10.3758/BF03195265. [DOI] [PubMed] [Google Scholar]
- Holliday RE, Hayes BK. Dissociating automatic and intentional processes in children’s eyewitness memory. Journal of Experimental Child Psychology. 2000;75:1–42. doi: 10.1006/jecp.1999.2521. [DOI] [PubMed] [Google Scholar]
- Holliday RE, Hayes BK. Automatic and intentional processes in children’s recognition memory: The reversed misinformation effect. Applied Cognitive Psychology. 2002;16:617–636. doi: 10.1002/acp.789. [DOI] [Google Scholar]
- Howe ML, Brainerd CJ. Development of children’s long-term retention. Developmental Review. 1989;9:301–340. [Google Scholar]
- Ingram KM, Mickes L, Wixted JT. Recollection can be weak and familiarity can be strong. Journal of Experimental Psychology: Learning, Memory, and Cognition. doi: 10.1037/a0025483. (in press) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jacoby LL. A process dissociation framework: Separating automatic from intentional uses of memory. Journal of Memory and Language. 1991;30:513–541. doi: 10.1016/0749–596X(91)90025-F. [DOI] [Google Scholar]
- Kintsch W, Morris CJ. Application of a Markov model to free recall and recognition. Journal of Experimental Psychology, 1965. 1965;69:200–206. doi: 10.1037/h0021588. [DOI] [PubMed] [Google Scholar]
- Koriat A. How do we know that we know? The accessibility model of the feeling of knowing. Psychological Review. 1993;100:609–639. doi: 10.1037/0033–295X.100.4.609. [DOI] [PubMed] [Google Scholar]
- Koriat A. Dissociating knowing and feeling of knowing: Further evidence for the accessibility model. Journal of Experimental Psychology: General. 1995;124:311–333. doi: 10.1037/0096–3445.124.3.311. [DOI] [Google Scholar]
- Koriat A, Levy-Sadot R, Edry E, de Marcas S. What do we know about what we cannot remember? Accessing the semantic attributes of words that cannot be recalled. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2003;29:1095–1105. doi: 10.1037/0278–7393.29.6.1095. [DOI] [PubMed] [Google Scholar]
- Kurilla BP, Westerman DL. Source memory for unidentified stimuli. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2010;36:398–410. doi: 10.1037/a0018279. [DOI] [PubMed] [Google Scholar]
- Langa K, Plassman B, Wallace R, Herzog AR, Heeringa S, Ofstedal MB, Willis R. The Aging, Demographics and Memory Study: Study design and methods. Neuroepidemiology. 2005;25:181–191. doi: 10.1159/000087448. [DOI] [PubMed] [Google Scholar]
- Lockhart RS, Murdock BB. Memory and theory of signal detection. Psychological Bulletin. 1970;74:100–109. doi: 10.1037/h0029536. [DOI] [Google Scholar]
- Malmberg KJ. Recognition memory: A review of the critical findings and an integrated theory for relating them. Cognitive Psychology. 2008;57:335–384. doi: 10.1016/j.cogpsych.2008.02.004. [DOI] [PubMed] [Google Scholar]
- Mandler G. Organization and memory. In: Spence KW, Spence JT, editors. The psychology of learning and motivation. Vol. 1. San Diego, CA: Academic Press; 1967. pp. 327–372. [Google Scholar]
- McCabe DP, Roediger HL, Karpicke JD. Automatic processing influences free recall: converging evidence from the process dissociation procedure and remember-know judgments. Memory & Cognition. 2011;39:389–402. doi: 10.3758/s13421–010–0040–5. [DOI] [PubMed] [Google Scholar]
- Morris JC, Heyman A, Mohs RC, Hughes JP, VanBelle G, Fillenbaum G, Clark C. The consortium to establish a registry for Alzheimer’s disease (CERAD). Part I. Clinical and neuropsychological assessment of Alzheimer’s disease. Neurology. 1989;39:1159–1165. doi: 10.1212/wnl.39.9.1159. [DOI] [PubMed] [Google Scholar]
- Osgood CE. The nature and measurement of meaning. Psychological Bulletin. 1952;49:197–237. doi: 10.1037/h0055737. [DOI] [PubMed] [Google Scholar]
- Petersen RC, Smith GE, Waring SC, Ivnik RJ, Tangalos EG, Kokmen E. Mild cognitive impairment: Clinical characterization and outcome. Archives of Neurology. 1999;56:303–308. doi: 10.1001/archneur.56.3.303. [DOI] [PubMed] [Google Scholar]
- Raj V, Bell MA. Cognitive processes supporting episodic memory formation in childhood: The role of source memory, binding, and executive functioning. Developmental Review. 2010;30:384–402. doi: 10.1016/j.dr.2011.02.001. [DOI] [Google Scholar]
- Ranganath C. Binding items and contexts: The cognitive neuroscience of episodic memory. Current Directions in Psychological Science. 2010;19:131–137. doi: 10.1177/0963721410368805. [DOI] [Google Scholar]
- Restle F. Significance of all-or-none learning. Psychological Bulletin. 1965;64:313–325. doi: 10.1037/h0022536. [DOI] [PubMed] [Google Scholar]
- Rey A. Psychological examination of traumatic encephalopathy. Archives de Psychologie. 1941;28:286–340. [Google Scholar]
- Reyna VF, Brainerd CJ. Fuzzy-trace theory: An interim synthesis. Learning and Individual Differences. 1995;7:1–75. doi: 10.1016/1041–6080(95)90031–4. [DOI] [Google Scholar]
- Reyna VF, Rivers SE. Current theories of risk and rational decision making. Developmental Review. 2008;28:1–11. doi: 10.1016/j.dr.2008.01.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Riefer DM, Batchelder WH. Multinomial modeling and the measurement of cognitive processes. Psychological Review. 1988;95:318–339. doi: 10.1037/0033–295X.95.3.318. [DOI] [Google Scholar]
- Rotello CM, Macmillan NA, Reeder JA. Sum-difference theory of remembering and knowing: A two-dimensional signal detection model. Psychological Review. 2004;111:588–616. doi: 10.1037/0033-295X.111.3.588. [DOI] [PubMed] [Google Scholar]
- Schacter DL, Worling JR. Attribute information and the feeling-of-knowing. Canadian Journal of Experimental Psychology. 1985;39:467–475. doi: 10.1037/0033–295X.111.3.588. [DOI] [Google Scholar]
- Schneider W, Pressley M. Memory development between two and twenty. Englewood Cliffs, NJ: Erlbaum; 1997. [Google Scholar]
- Sharot T, Yonelinas AP. Differential time-dependent effects of emotion on recollective experience and memory for contextual information. Cognition. 2008;106:538–547. doi: 10.1016/j.cognition.2007.03.002. [DOI] [PubMed] [Google Scholar]
- Strong EK. The effect of time-interval upon recognition memory. Psychological Review. 1913;20:339–371. doi: 10.1037/h0072087. [DOI] [Google Scholar]
- Tulving E. Memory and consciousness. Canadian Psychologist. 1985;26:1–12. doi: 10.1037/h0080017. [DOI] [Google Scholar]
- Tulving E, Thomson DM. Encoding specificity and retrieval processes in episodic memory. Psychological Review. 1973;80:352–373. doi: 10.1037/h0020071. [DOI] [Google Scholar]
- Tunney RJ. Do changes in the subjective experience of recognition over time suggest independent processes? British Journal of Mathematical and Statistical Psychology. 2010;63:43–62. doi: 10.1348/000711009X416416. [DOI] [PubMed] [Google Scholar]
- Underwood BJ, Ekstrand BR, Keppel G. An analaysis of intralist similarity in verbal-learning with experiments on conceptual similarity. Journal of Verbal Learning and Verbal Behavior. 1965;4:447–462. doi: 10.1016/S0022–5371(65)80042–1. [DOI] [Google Scholar]
- Viskontas IV, Carr VA, Engel SA, Knowlton BJ. The neural correlates of recollection: Hippocampal activation declines as episodic memory fades. Hippocampus. 2009;19:265–272. doi: 10.1002/hipo.20503. [DOI] [PubMed] [Google Scholar]
- Waugh NC, Smith JA. A stochastic model for free recall. Psychometrika. 1962;27:141–145. doi: 10.1007/BF02289631. [DOI] [Google Scholar]
- Wixted JT. Dual-process theory and signal-detection theory of recognition memory. Psychological Review. 2007;114:152–176. doi: 10.1037/0033–295X.114.1.152. [DOI] [PubMed] [Google Scholar]
- Yonelinas AP. Receiver-operating characteristics in recognition memory: Evidence for a dual-process model. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1994;20:1341–1354. doi: 10.1037/0278–7393.20.6.1341. [DOI] [PubMed] [Google Scholar]
- Yonelinas AP. The nature of recollection and familiarity: A review of 30 years of research. Journal of Memory and Language. 2002;46:441–518. doi: 10.1006/jmla.2002.2864. [DOI] [Google Scholar]