Figure 5. Chaotic motifs described by .

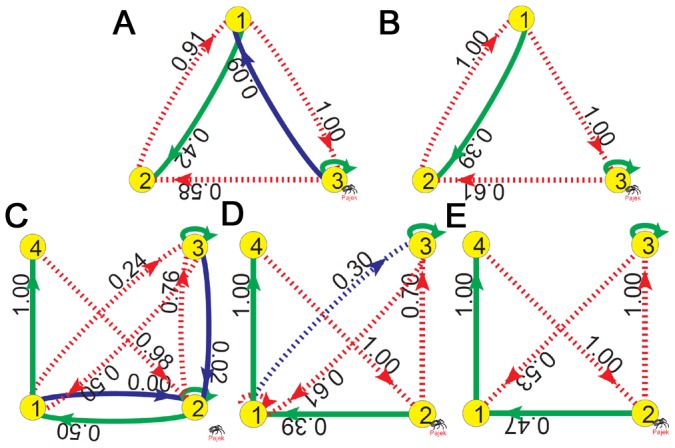
distributions of the chaotic GRNs of Figs.1 and 2. A for Fig.1A; B for Fig.1D; C for Fig.2A; D for Fig.2B; E for Fig.2C. The numbers associated to all cross interactions indicate the of Eq.(7). The total period of measurement is about 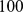cycles of chaotic orbits. It is shown that most of the interactions reducible for chaos have almost zero , while all the interactions irreducible for chaos in the chaotic motifs in Fig.1D and Fig.2C have sufficiently large . Note that, the two interactions and 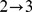in D have comparable 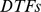. Discarding different one of them can construct different chaotic motifs (motifs (22) and (67) in Fig. S1 by discarding 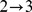and 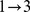, respectively). On the other hand, both the interactions of 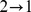and 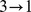in D are important for the competition between the two loops and thus essential for chaos. There is only one loop in the GRN after removal of 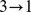(breaking condition (i)); and the PFL is included in the NFL after deletion of 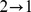(breaking condition (iii)), and both of the two operations can securely suppress chaotic motions.