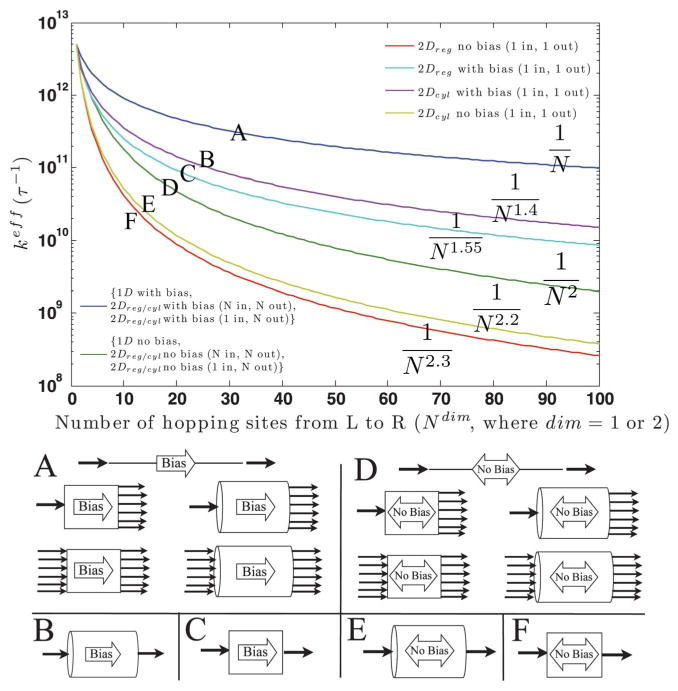
Fig. 5.

The hopping number dependence of the mean rate through a 1 or 2 dimensional bridge. The injection into and ejection out of the bridge were modeled as irreversible for each scenario in order to achieve a net flux from L to R. Lines labeled “with bias” have all backward rate constants set to zero. All other rate constants were k = 10¹³ s⁻¹. “No bias” means forward and backward rate constants were equal, excepting the injection and ejection rate constants which have no backward rate. 2D_reg refers to a “regular” 2D lattice of hopping sites. 2D_cyl refers to a cylindrical and therefore periodic lattice of hopping sites. From the figure, one can estimate order of magnitude drops in the effective rate constant as a function of the number of hopping steps, with the assumption that all hopping rate constants throughout the kinetic scheme are equal. The effective rate constants decay by a power law with the number of sites, N. Each line is labeled with its fitted distance dependence and a letter A through F, corresponding to its diagramatic representation below.