Self-Feedback in Actin Polymerization

Abstract

Polymerization of actin, which is crucial for functions such as cell migration, membrane ruffling, cytokinesis, and endocytosis, must be tightly regulated in order to preserve an adequate supply of free actin monomers to respond to changing external conditions. The paper will describe mechanisms by which F-actin feeds back on its own assembly, thus regulating itself. I will present the experimental evidence for such feedback terms, discusse their use in current models of actin dynamics in cells, and present preliminary calculations for the role of feedback in transient endocytic actin patches. These calculations suggest a partial homeostasis of F-actin, in which the F-actin peak height depends only weakly on the actin filament nucleation rate.

1 Introduction

The precise regulation of actin polymerization is crucial for appropriate polymerization of actin in response to external stimuli, or for the internal dynamics of cells exploring their local environment. Upstream regulation of actin polymerization has both positive elements, which enhance actin polymerization, and negative elements, which inhibit it. Well-established positive elements include nucleation-promoting factors (NPFs), which act upstream of proteins/complexes nucleating new actin filaments [1]. These proteins include the Arp2/3 complex, which generates new actin filaments as branches on existing filaments, and formins, which generate new filaments in the absence of preexisting filaments. Well-known negative elements include severing and depolymerization induced by proteins such as cofilin. Actin has a bound nucleotide, ATP or ADP or an intermediate state denoted ADP-P_i. The hydrolysis of ATP-actin to ADP-actin favors depolymerization, and this process is accelerated by cofiln. In addition to such top-down control, feedback mechanisms can be useful in tailoring the dynamic response of cells to stimuli [2]. Positive feedback can lead to strong rapid responses, and negative feedback to stability or homeostasis. Positive F-actin feedback motifs could thus be useful in obtaining a rapid response to stimuli favoring polymerization, while negative feedback motifs could avoid excessive F-actin accumulation. The combination of positive feedback and delayed negative feedback could also provide an mechanism for rendering F-actin dynamic - in the sense of causing F-actin acccumulations to be transient. This article outlines the experimental evidence for such feedback, explores possible feedback circuits embodying both positive and negative feedback, reviews the use of such circuits in recent theories of actin dynamics in cells, and presents preliminary results for the protein dynamics of endocytic actin patches based on a three-state model. Calculations of the F-actin peak height as a function of the filament nucleation rate gives a weak dependence, suggesting a partial homeostasis mechanism.

It is important to distinguish between ”direct” and ”indirect” feedback. ”Direct” feedback occurs on a rapid enough time scale that the assembly or disassembly of F-actin at a given time is effectively proportional to the amount of F-actin present at that time; ”indirect” feedback occurs after a delay, which may be generated by one or more intermediate nodes in a signaling pathway. This distinction is important because direct positive and direct negative feedback will cancel each other, simply leading to a reduced magnitude of feedback; on the other hand direct positive feedback combined with delayed negative feedback can lead to oscillatory behavior.

2 Experimental Evidence for Positive and Negative Self-Feedback of F-Actin

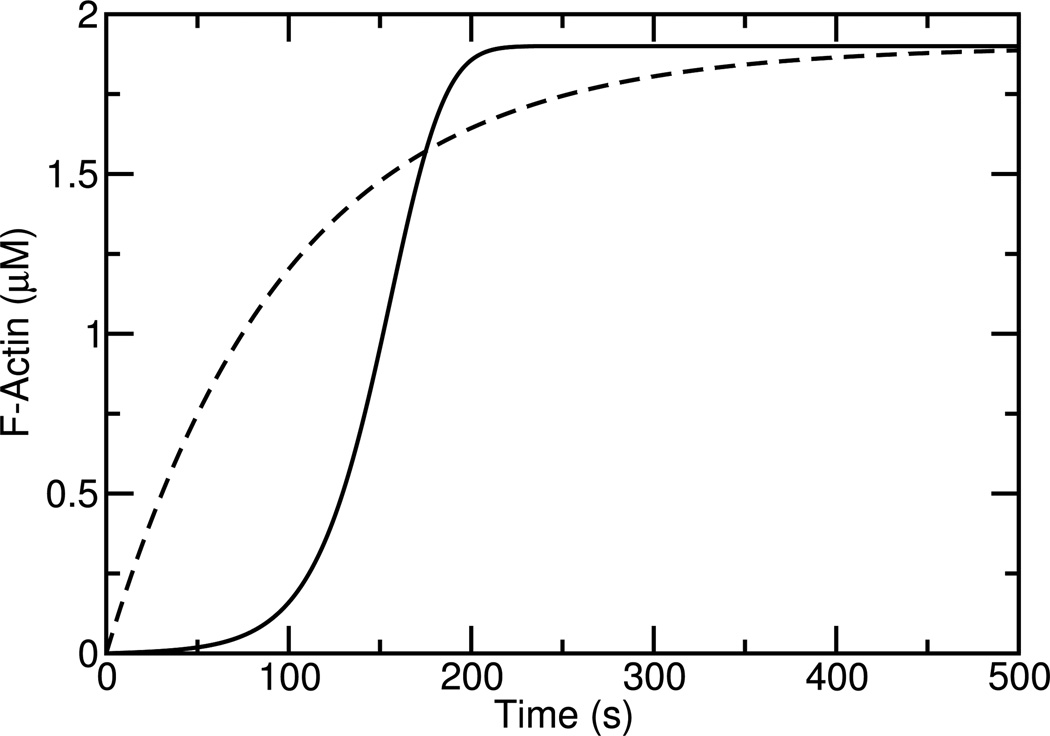
Evidence for positive feedback of F-actin lies in the dynamics of actin polymerization in vitro induced by Arp2/3 complex. The Arp2/3 complex, when activated by upstream agents such as NPFs, forms new growing branches on the sides of existing filaments both in cells and in vitro. Because the rate of nucleation of new filaments increases with the amount of F-actin present, a small number of filaments can rapidly multiply and the F-actin concentration initially grows exponentially. This means that the time course of polymerization often appears to have a ”lag phase”, where polymerization is limited, followed by an explosive growth of polymerization. Fig. 1 compares time courses of actin polymerization assuming positive feedback (solid line), in which the number of filaments increases proportionally to the F-actin concentration, and no feedback (dashed line), in which the number of filaments is constant. The positive-feedback curve clearly demonstrates a lag phase, followed by a rapid jump to the final value which is the total actin concentration minus the critical concentration. The no-feedback curve increases much less dramatically. There are many examples of Arp2/3-induced polymerization time courses in the literature which are similar to the positive-feedback curve shown here [3, 4, 5, 6, 7]. The positive feedback involves two steps, the generation of new free barbed ends on existing filaments, and the growth of these filaments to generate new F-actin.

Fig. 1.

Schematic of actin polymerization with (solid line) and without (dashed line) positive feedback. Curves obtained using rate equations described in Ref. [5] with arbitrary parameters.

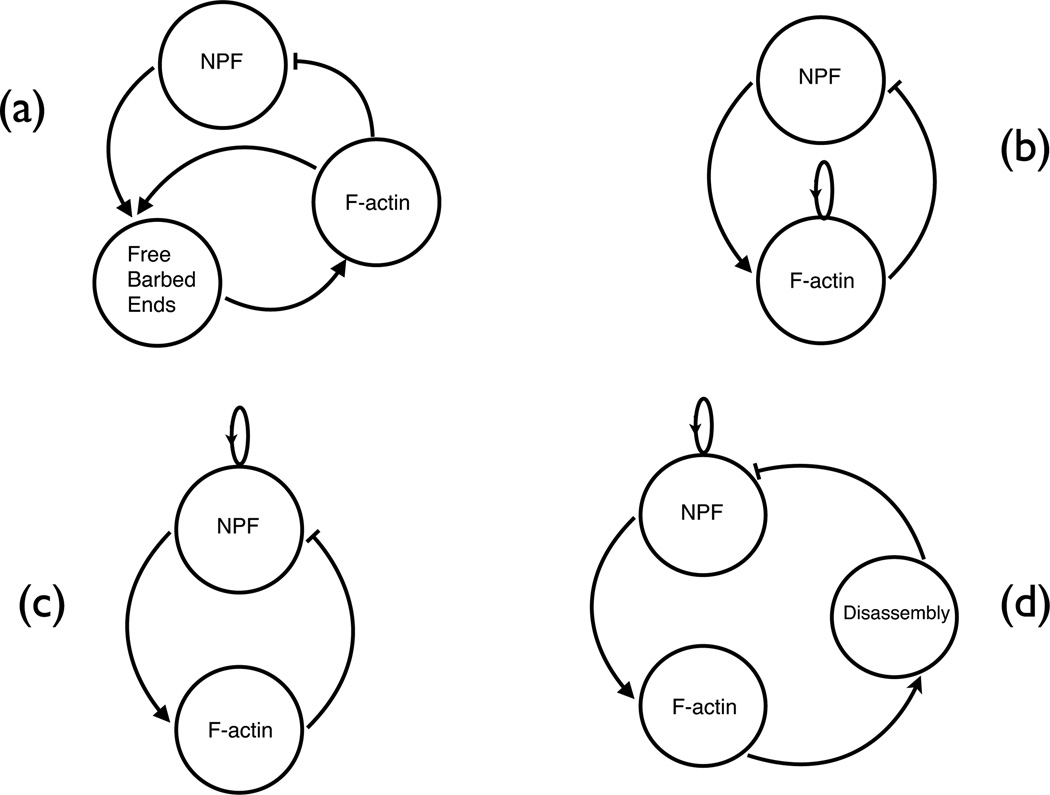
This is indicated by the positive-feedback lines in Fig. 2a. Thus it is in principle an indirect feedback mechanism. However, if the delay between the generation of new filaments and the subsequent F-actin accumulation is small, the feedback may be considered direct, for practical purposes. This delay is determined by the lifetime of a free barbed end, which is determined by the capping rate. In general, capping rates in cells are on the order of 1s⁻¹, which is faster than most of the dynamic F-actin processes to be discussed below. Therefore positive feedback of F-actin may legitimately be viewed as direct, as indicated in Fig. 2b.

Fig. 2.

Possible F-actin feedback circuits generating F-actin dynamics. Arrows indicate positive feedback and bars at ends of lines indicate negative feedback. Loops indicate positive feedback.

Evidence for indirect negative feedback of F-actin, as indicated by the negative feedback lines in Fig. 2, comes from studies in cells and in vitro. Weiner et al [8] measured the dynamics of the Hem-1 component of the WAVE2 complex in neutrophils, an NPF. The WAVE2 complex acts upstream of actin polymerization by activating Arp2/3 complex, and is required for proper leading edge morphology; its homologues regulate cell shape and movement in a variety of organisms. Weiner et al performed fluorescence recovery after photobleaching (FRAP) experiments using fluorescently labeled Hem-1. In these experiments, a 1 – 2 µm spot was bleached, and the recovery was followed as a function of time. The recovery involves Hem-1 leaving the membrane and being replaced. The experiments were performed both in the presence and absence of latrunculin, an agent which inhibits actin polymerization. It was found that latrunculin greatly slowed the recovery process. This implies that actin polymerization is essential for the dynamics of Hem-1 leaving and entering the membrane.

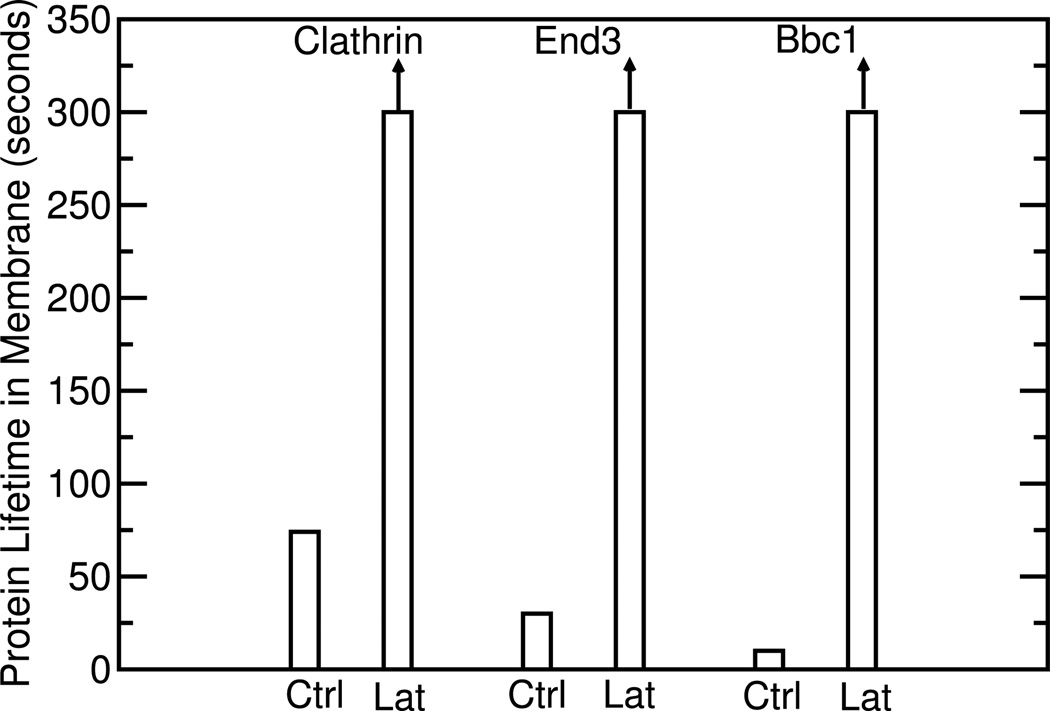
Kaksonen et al ([9] evaluated the effects of F-actin on the lifetimes of proteins acting upstream of actin in transient protein patches occurring during endocytosis in budding yeast. Under control conditions, a number of proteins, including Clc1, Bbc1, and End3, assemble first. These are followed by F-actin, and then by a series of proteins, including cofilin, which disassembles F-actin. It was found that suppression of actin polymerization by the addition of latrunculin greatly lengthened the lifetimes of Clc1, Bbc1, and End3, as indicated in Fig. 3. This shows that F-actin disassembles proteins which act upstream of actin polymerization, thus demonstrating an indirect negative feedback loop, as in Fig. 2.

Fig. 3.

Lifetimes of endocytic coat proteins, under control conditions (Ctrl) and with latrunculin (Lat). Data taken from Ref. [9]. Arrows mean that bars are lower bounds for lifetimes.

In vitro studies [10] have shown that F-actin inhibits the Abl tyrosine kinase, which regulates actin polymerization [11]. Measurement of purified Abl-kinase activity as a function of increasing F-actin concentration revealed a steady drop. Furthermore, time-dependent growth of Abl-kinase activity was found to be inhibited by F-actin.

Ganguly et al studied the effect of serotonin receptor activity on actin polymerization [12] in Chinese hamster ovary (CHO) cells, and conversely the effect of F-actin on receptor mobility and activity [13]. It was found that serotonin-mediated activation of the receptor led to increased F-actin content, presumably through inhibition of the production of cyclic AMP (cAMP), which causes actin depolymerization. F-actin, in turn, inhibited serotonin receptor mobility, which was found to reduce the receptor efficiency. These observations, taken together, suggest a multistep negative feedback loop of the type shown in Fig. 2d, where the disassembly module summarizes effects of F-actin on receptor mobility/efficiency, the effects of serotonin receptors on cAMP production, and the pathways allowing cAMP to depolymerize F-actin.

3 Calculations of the Effect of Self-Feedback on F-actin Dynamics in Cells

Mathematical modeling of F-actin dynamics in cells has shown that the types of feedback effects discussed here can lead to the formation of spontaneous dynamic phenomena such as F-actin waves and patches [14]. These models have used feedback architectures of the types illustrated in Fig. 2. The general mechanism by which such feedback loops lead to transient F-actin structures, using Fig. 2c for concreteness, is the following. Positive feedback of NPF causes a small fluctuation of NPF to grow. F-actin then builds up because NPF activates F-actin. Since F-actin inhibits NPF, the NPF will drop to zero after a while, and subsequently the F-actin will drop to zero. If diffusion is present, this can result in traveling waves or patches.

Two models in the literature [8, 15] used an architecture of the type shown in Fig. 2c. These models led to spontaneous waves of F-actin and the NPF Hem-1; Ref. [15] also found actin patches under some conditions. Other models have used positive F-actin feedback to treat the spontaneous formation of F-actin waves and patches in Dictyostelium. The model of Ref. [16] used a feedback circuit of the form shown in Fig. 2b, and assumed spontaneous polarization of filament orientations and diffusionlike spreading of F-actin. These assumptions were found to lead to the formation of patches which eventually coalesced into traveling waves. The treatment of [17] implemented the circuit of Fig. 2a, using a dendritic-nucleation model of actin filament generation, in which new filaments are generated as branches on existing filaments by the action of NPFs in the plasma membrane. The calculations were performed using a stochastic-growth methodology in which explicit three-dimensional network structures were generated, and dendritic filament clusters moved by Brownian motion. This avoided the explicit parameterization of positive-feedback and diffusion effects; instead, these effects emerged naturally from the known biochemistry. The calculations revealed, with increasing actin concentration, a series of phases beginning with patches, subsequently waves, and finally a phase which could not be described in terms of either traveling waves of patches, but still displayed fluctuations which appeared to be strongly out of equilibrium. Fig. 4 shows an example of the wave phase. A forest of actin filaments is seen moving to the left. The ”story line” of the motion is as follows: 1) there is a high concentration of membrane-bound (active) NPF ahead of the wave; 2) F-actin grows into this region; and 3) the F-actin removes and inactivates the NPF, causing subsequent depolymerization of F-actin at the back of the wave.

Fig. 4.

Progression of actin wave in stochastic-simulation approach (Ref. [17]). Red rods denote actin filaments; substrate-bound membrane of cell is green.

A larger set of feedback interactions has been treated in a recent study of endocytosis in budding yeast [18]. During this process, actin patches form at the cortex and, disappear after approximately 20 seconds. The model used has roughly the structure of Fig. 2d. NPF was assumed to assemble in response to membrane-bound PIP2, which had a positive-feedback rate law. F-actin, rather than directly inhibiting NPFs, was taken to cause membrane curvature. This curvature, in turn, caused PIP2 hydrolysis, which reduced NPF accumulation. In other words, the ”disassembly” bubble in Fig. 2d would include curvature and PIP2 hydrolysis - a multistep negative feedback of F-actin on NPFs. This set of assumptions led to the appearance of transient patches, and made several predictions about the effects of key rates on the success of endocytosis.

4 The Systems Biology of a Transient Actin Patch

Motivated by the modeling of Ref. [18], we have attempted to abstract the key ingredients required to obtain transient actin patches by using a simpler model, based on Fig. 2d, with only one variable in the ”disassembly” bubble. We do not specify the physical nature of this variable, but rather deduce its dynamics from its impact on the assembly/dissasembly of the NPF module and F-actin. Because of this simplicity, it is straightforward to evaluate the effects of key rates on measurable output properties. The model has three variables. The first, [N], includes the coat proteins which arrive first in endocytosis, and the NPFs; the second, [F], includes F-actin and associated actin-binding proteins such as Arp2/3 complex and capping protein; and the third [D], includes the factors that are most important in dissembly of the coat proteins.

The initial assembly of the coat protein/NPFs is assumed to proceed by the generation of accumulation nuclei from membrane proteins in a restricted ”corral” region. The nuclei grow when their size exceeds a critical size. The equations of motion are:

$$\frac{d[N]}{\mathit{\text{dt}}}=k_N^{+}(N_0-[N])-k_N^{+}{N}_0\text{exp}[{\epsilon }_s(1/\sqrt{N}-1/\sqrt{N_c})]-k_N^{-}{[D]}^i[N]$$ (1)

$$\frac{d[F]}{\mathit{\text{dt}}}=k_F^{+}{[N]}^j-k_F^{-}[F]$$ (2)

$$\frac{d[D]}{\mathit{\text{dt}}}=k_D^{+}[F]-k_D^{-}[D]$$ (3)

Here N₀ is the initial number of coat/NPF proteins in the corral, N_c is a critical cluster size, and ε_s is a dimensionless surface energy parameter; i and j are powers characterizing the cooperativity of NPFs in assembling actin and the nonlinearity of coat/NPF disassembly. The k’s are on- and off-rate parameters for the three species. The cooperativity of the NPFs in assembling actin (j) is based on experimental observations indicating a high degree of cooperativity in the activity of the NPF WASp [19], which has the analog Las17 in yeast. The cooperativity in disassembly (i) could come from several sources [18], one of which is an exponential dependence of coat protein off-rates on membrane curvature.

The form of Eq. (1) is motivated by classical nucleation theory [20], in which the ratio of the on-rates to the off-rates is determined by the free energy of cluster formation and its dependence on cluster size; the square-root terms in Eq. (1) reflect the contribution of the surface energy (which is proportional to $\sqrt{N}$ for a protein patch growing in two dimensions). Note that the factor in front of the exponential can safely be taken to be $k_N^{+}$, since adjusting this factor is equivalent to adjusting N_c.

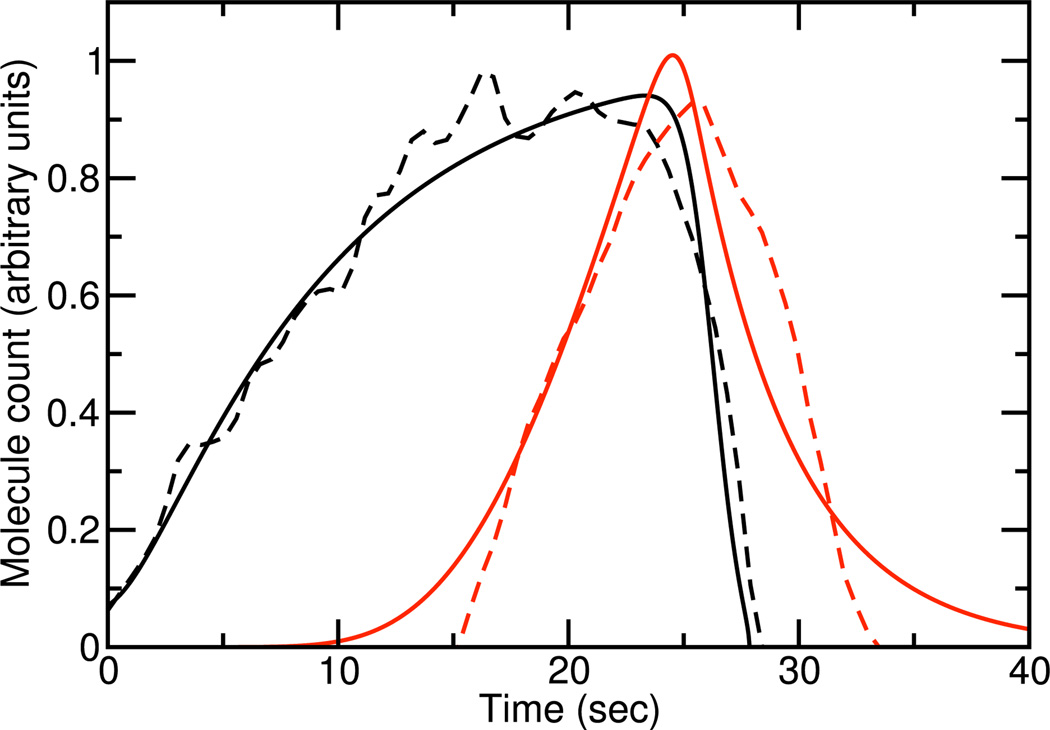
The parameters in this model were adjusted to fit measured data for the dependence of a coat protein/NPF (Las17) and F-actin (as indicated by the actin-binding protein Abp1) in budding yeast. The parameters adjusted were: an overall factor scaling the model results to the experimental data, $k_N^{+},k_F^{+},k_F^{-},\text{and}{k}_D^{+}$. The parameter $k_N^{-}$ was assigned a fixed value since changes in $k_N^{-}$ can be compensated for by changes in the normalization of [D], and [D] is not included in the fitting database. To reduce the number of fitting parameters, and because disassembly of D is expected to at least partly require disassembly of F, it was assumed that $k_D^{-}=0.25k_F^{-}$. The exponents i and j were assigned the value 8; smaller values than this tended to give a worse fit to the data. As shown in Fig. 5, the modeling at this level gives a good fit to the averaged patch-count data. The life cycle of the patch is that first NPF builds up, causing F-actin buildup; the F-actin in turn causes disassembly factors to build up, which disassemble the NPF patch.

Fig. 5.

Solid lines: time courses of coat/NPF (black) and F-actin (red) obtained from deterministic simulations Dashed lines denote experimental data from Ref. [9].

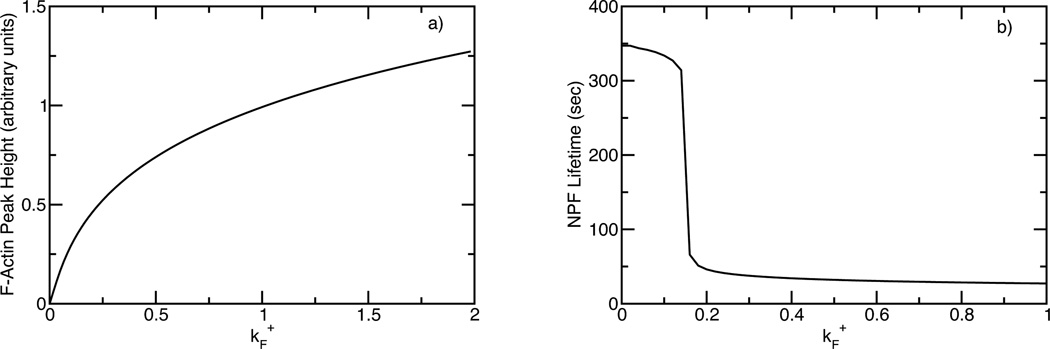
This model makes several predictions regarding the behavior of key observables on underlying rates and concentrations. For example, $k_F^{+}$ is expected to influence the height and lifetime of the actin peak, and thus the NPF lifetime as well. Fig. 6 shows the dependence of the F-actin peak height and the patch lifetime on $k_F^{+}$. It is seen that the peak height increases with $k_F^{+}$, but at a rate slower than linear. The slowness of the increase is a manifestation of the negative feedback loop connecting F-actin with itself: increased F-actin at a certain time leads to increased dissasembly agent buildup, which in turn removes NPF and inhibits actin polymerization. On the other hand, decreasing $k_F^{+}$ relative to its fitted value has little effect until it is quite small; then the lifetime climbs very rapidly. (The ”shelf” at small $k_F^{+}$ should be viewed as a lower bound, because the simulations were only run out to 400 s.) These predictions could be tested by currently available experimental techniques. Since $k_F^{+}$ is expected to increase with increasing actin concentration, agents such as latrunculin, which sequester free actin monomers, should reduce $k_F^{+}$. Similarly, mutations in those NPF domains which activate Arp2/3 complex directly or indirectly [21] should lead to reduced $k_F^{+}$. This theory predicts that such mutations, unless they affect all or nearly all NPF activators, would have little effect on the F-actin peak height. This may be viewed as a partial homeostasis mechanism in which the F-actin peak height is robust to weak perturbations.

Fig. 6.

F-actin peak height (a) and NPF patch lifetime (b) as functions of actin polymerization/nucleation parameter $k_F^{+}$, which is given in units of the best-fit value from the fits in Fig. 5.

5 Summary

Several lines of evidence indicate that F-actin, rather than simply following its upstream activators passively, feeds back on its own production in ways that can either enhance or inhibit polymerization, depending on time scale. Such feedback effects may be a key factor in regulating transient F-actin accumulations such as those in F-actin waves or endocytic patches, and in stabilizing quantities such as the F-actin peak height to perturbations in underlying rate parameters.