Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2012 Jul 18;2:519. doi: 10.1038/srep00519

Tuning Charge and Spin Excitations in Zigzag Edge Nanographene Ribbons

Sudipta Dutta 1, Katsunori Wakabayashi 1,a
PMCID: PMC3399123  PMID: 22816042

Abstract

Graphene and its quasi-one-dimensional counterpart, graphene nanoribbons, present an ideal platform for tweaking their unique electronic, magnetic and mechanical properties by various means for potential next-generation device applications. However, such tweaking requires knowledge of the electron-electron interactions that play a crucial role in these confined geometries. Here, we have investigated the magnetic and conducting properties of zigzag edge graphene nanoribbons (ZGNRs) using the many-body configuration interaction (CI) method on the basis of the Hubbard Hamiltonian. For the half-filled case, the many-body ground state shows a ferromagnetic spin-spin correlation along the zigzag edge, which supports the picture obtained from one-electron theory. However, hole doping reduces the spin and charge excitation gap, making the ground state conducting and magnetic. We also provide a two-state model that explains the low-lying charge and spin excitation spectrum of ZGNRs. An experimental setup to confirm the hole-mediated conducting and magnetic states is discussed.

Carbon nanomaterials have gained sustained interest in recent times due to their fascinating electronic properties, which arise from electronic confinement in a reduced-length scale. The successful isolation of graphene by mechanical exfoliation1,2,3 has provided further impetus and has allowed for the first time the understanding of various properties in a truly two-dimensional context4,5,6. The ultrahigh charge carrier mobility, transparency and mechanically flexible properties of graphene provide an excellent platform for futuristic device applications7.

Another intriguing aspect of graphene is the strong nanoscale and edge effects on its electronic and magnetic properties. The quasi-one-dimensional ZGNRs have drawn particular attention because of their peculiar edge ferrimagnetism that arises from the edge-localised states near the zigzag edges8,9,10. Intensive studies ranging from mean-field to density functional theory have been performed to understand the carbon-based magnetism in ZGNRs11,12,13,14. A recent experiment using scanning tunnelling spectroscopy (STS) reports the splitting of the density of states due to the edge magnetism for chiral graphene nanoribbons15.

These theoretical and experimental studies have motivated the fabrication of spintronics devices based on graphene nanoribbons. Although its edge-state magnetism seems to contradict the Mermin-Wagner theorem, which rules out the possibility of long-range ordering in quasi-one-dimensional systems16, a recent theoretical report using quantum Monte Carlo supports the existence of such a long spin-spin correlation length along the zigzag edge and justifies the picture obtained from the one-electron theories17. Moreover, many previous studies suggest various ways to tweak the electronic properties of ZGNRs to achieve magneto-transport by means of doping, chemical modifications or external perturbations18,19,20,21,22.

From the viewpoint of device applications, it is necessary to clarify the interplay between the edge magnetism and the hole-doping effect, as the electron density in the graphene system can be easily tuned using the back gate electrode23,24,25. However, the hole-doping effect on edge magnetism has not been studied with the appropriate inclusion of electron-electron interactions.

In this study, we theoretically investigate the magnetic and conducting properties of ZGNRs and their response to doping. The development of gapless charge and spin excitations with hole doping, i.e., hole-mediated metallic ferromagnetism, is also discussed for the first time in terms of its potential applications. Our theoretical analysis is based on a large-scale numerical simulation using the many-body configuration interaction (CI) method with the complete active space (CAS-CI) approximation, which correctly includes quantum fluctuations. We show that the microscopic origin of magnetism in ZGNRs can be well understood on the basis of a generic two-state model.

Results

We model the systems within a Hubbard Hamiltonian with onsite electron-electron interactions. The Hamiltonian reads as

graphic file with name srep00519-m1.jpg

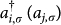where Inline graphic creates (annihilates) one electron with spin σ on site i and ni,σ is the number operator. “U” denotes the onsite Coulomb interaction, and the nearest neighbour hopping integral "t" has been set to unity. We restrict our calculations within the weak coupling limit and consider the U/t ratio as one. This assumption ensures the absence of polarisation of spins for the bulk sites in the graphene. Note that the above Hamiltonian conserves the electron-hole symmetry, and therefore, hole doping and electron doping are expected to show identical behaviour.

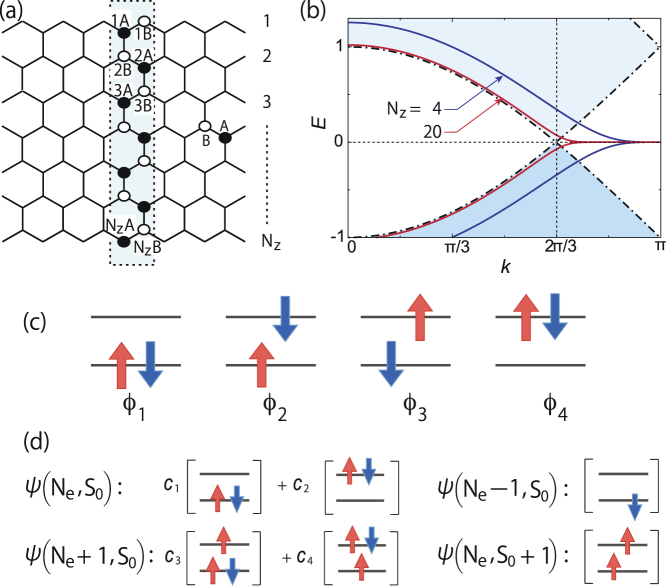
Figure 1a shows a schematic representation of the ZGNRs. The lattice constant has been considered to be unity. The width of the ZGNRs is defined by the number of zigzag lines (Nz) along the transverse ribbon direction. The edges are assumed to be passivated by hydrogen atoms, and therefore, the electronic states near the Fermi energy remain unaltered. Within the non-interacting case, the top of the valence band and the bottom of the conduction band are partially flat between k = π (the Brillouin zone (BZ) boundary) and k = 2π/3 (the Dirac point) at the Fermi energy. As shown in Figure 1b, this flat region increases with increasing ribbon width.

Figure 1. Geometry and band structure of ZGNRs with two-state model.

Figure 1

Open in a new tab

(a) The structure of ZGNR, with Nz being the width. The unit cell (dashed rectangle) consists of same number of A (filled circles) and B (open circles) sublattice points. (b) Tight binding energy spectrum of ZGNR in momentum (k) space. The top of the valence band and the bottom of the conduction band of ZGNRs with Nz = 4 and 20 are depicted as the solid lines. These two central subbands construct the two-state model. The shaded region designates the bulk graphene spectrum near the Fermi energy (E = 0) with linear dispersion around Dirac point (k = 2π/3). 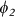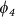(c) The four basis states ( Inline graphic, Inline graphic, Inline graphic and Inline graphic ) to construct the two-state model for half-filled system with Sztot = 0. (d) Ψ(Ne,S0) is the wave function for the ground state for half-filled system. Ψ(Ne + 1,S0) and Ψ(Ne - 1,S0) are the wave functions for the system with one more and one less electron than half-filling, respectively. Ψ(Ne,S0 + 1) represents the ground state of half-filled system with Sztot = 1. The wave function coefficients are represented in terms of c.

We calculate the many-body charge gap (Δc) and spin gap (Δs) and their response to the hole doping as follows26,27:

graphic file with name srep00519-m3.jpg
graphic file with name srep00519-m4.jpg

Here, E0(Ne,S0) represents the lowest energy in the subspace of Ne ( = N−nh) electrons, where nh denotes the number of holes doped in the half-filled system (N) with the lowest Sztot (the z-component of total spin) = S0 ( = 0 or 1/2 for even or odd Ne, respectively) at each k-point. In this paper, to probe the different spin sectors, we vary the Sztot. The number of electrons and Sztot both commute with the Hubbard Hamiltonian and therefore can be used as good quantum numbers. Note that the Δc and Δs are calculated at discrete k-points, and the scattering processes connecting the different k-points are neglected. This approximation occasionally fails to capture the essential physics of spin excitations in the case of narrow ribbons, which will be discussed in the spin gap section. However, the low energy charge and spin excitation properties for wider ribbons can be satisfactorily captured by this approximation, as is evident from our calculations for finite size systems in the latter part of the article.

Two-state model

In a weak coupling regime, the charge and spin excitation properties of the ZGNRs are governed by two bands (shown in Fig. 1b). Thus, the whole problem can be effectively mapped into a two-state model for the half-filled case. At each k-point, the two-state model is defined by four possible basis states, as shown in Figure 1c. In the U = 0 limit, the system is stabilised only by kinetic energy, and the ground state is defined only by Inline graphic.

Before showing the detail of the two-state model, we shall try to avoid confusion between molecular orbital space and real space descriptions, as the two-state model is constructed in molecular orbital space rather than in real space. Let us first discuss the simplest example of a system with two atomic sites. As we know, in real space, the introduction of U begins localising one electron at each atomic site. Therefore, the ground state for half-filling and Sztot = 0 with non-zero U can be represented as a singlet state, 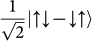Inline graphic, in real space. In molecular orbital space, this ground state can be described as 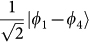Inline graphic, which corresponds to Ψ(Ne,S0) with equal c1 and c2, as shown in Figure 1d within the two-state model. 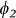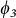Note that Inline graphic and Inline graphic contribute to the excited states but not to the ground state.

The charge excitation process can be understood based on the two-state model as follows. The effect of U becomes more pronounced over the flat band region (2π/3 ≤ k ≤ π for wide ZGNRs), as the on-site Coulomb interaction, U, is effectively evaluated as U/W, where W is the bandwidth28. Because W is very small over the flat band region for any U > 0, the effective interaction becomes very high. 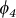Thus, the ground state, Ψ(Ne,S0), is described as a linear combination of Inline graphic and Inline graphic (see Fig. 1d), which has been confirmed by analysing the coefficients of the wavefunctions obtained from the CI calculations. However, as we move away from the flat band region (|k| ≤ 2π/3), the decrease in U/W increases the contribution of 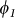Inline graphic to the ground state.

In the case of one fewer electron than half-filling, the ground state is singly occupied in the lower flat band and is expressed as Ψ(Ne - 1,S0), as shown in Figure 1d. Due to the single occupancy, this state is independent of the parameter U. However, the state with one more electron than half-filling cannot avoid the pairing of electrons, and hence the ground state, Ψ(Ne + 1,S0), costs U amount of energy. Therefore, the difference between E0(Ne +1,S0) and E0(Ne−1,S0) always remains U26. Thus, the charge gap, Δc, is solely determined by the relative position of E0(Ne,S0) with respect to the states with one extra and one fewer electron. This behaviour will be confirmed in the CAS-CI calculation later.

The two-state model provides a microscopic understanding of the spin gap behaviour within the many-body framework. Because in the spin excited state, Ψ(Ne,S0 +1) (shown in Fig. 1d), the valence and conduction bands are occupied by single electrons with the same spin, its energy E0(Ne,S0 +1) becomes independent of U. Thus, Δs is determined only by E0(Ne,S0). The most intriguing behaviour of the zero spin gap is observed when Ψ(Ne,S0) has equal contributions from 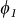Inline graphic and Inline graphic. The top of the valence band is doubly occupied in the Inline graphic configuration, whereas in the Inline graphic configuration, the bottom of the conduction band is doubly occupied (see Fig. 1d). When each of them contributes 50% to construct the ground state, it effectively becomes similar to the state with single occupancy of the top of the valence band and the bottom of the conduction band. Therefore, the energy of the ground state, E0(Ne,S0), becomes equal to the energy of the spin excited state, E0(Ne,S0 +1), closing the spin gap. This criterion actually can be satisfied in the flat band region, where U/W is large enough. Because of the vanishing W over this region, any U > 0 is enough to make the ground state a magnetic state. This magnetic ground state, arising from degenerate flat bands near the Fermi energy, is analogous to Mielke's flat band ferromagnetism29,30.

Charge gap

We characterise the conducting properties of ZGNRs by evaluating the charge gap, Δc, which is the energy difference between charging and discharging an electron to the system. The decrease in the charge gap indicates the enhancement of conduction behaviour. Our theoretical analysis supports the pictures obtained from one-electron theory regarding charge excitation.

Figure 2a shows the charge gap Δc for half-filled ZGNRs over the BZ using CAS-CI. The observations within the two-state model remain unchanged even for higher numbers of bands in the CAS-CI calculations, where 4900 numerical basis states were considered. The minimum in Δc decreases and shifts towards the Dirac point with increasing width to resemble the conical spectrum of bulk graphene. The minimum charge gap, Δc(min.), varies inversely with the width of the ZGNRs (see Fig. 2b) and approaches zero at infinite width, i.e., bulk graphene. All of these observations are qualitatively in agreement with the one-electron approaches such as mean-field or local density approximation (LDA)15,21 and with the analytic results31. Interestingly, in this weak coupling regime, the Δc at BZ boundary (k = π) is exactly equal to the U/t ratio and remains unaltered with increasing width (see Fig. 2b). This equality originates from the fact that at k = π, the ground state energy has a vanishing contribution from the kinetic energy term of the Hubbard Hamiltonian and is governed only by the interaction parameter. In the weak coupling regime, the half-filled system and the system with one fewer electron both become the ground state of the interacting part of the Hamiltonian, and thus, the energy of removing one electron from the half-filled state amounts to zero at k = π, resulting in a charge gap of U/t.

Figure 2. Charge gap, spin gap and spin density of half-filled ZGNRs.

Figure 2

Open in a new tab

(a) The charge gap (Δc) behavior over the BZ for ZGNRs with Nz = 4 and 20 (solid lines) and for bulk graphene (dashed line) at half-filling. (b) The minimum of charge gap, Δc (min.) (circles) near the Dirac point as a function of Nz and fitted (solid line) with the equation: Δc = 1.736/ Nz. The Δc at k = π for varying Nz is shown by dashed line with squares. (c) The spin gap (Δs) behavior over the BZ for ZGNRs with Nz = 4 and 20 (solid lines) and for bulk graphene (dashed line) at half-filling. (d) and (e) shows the spin density profile of half-filled ZGNR with Nz = 20 for Sztot = S0 and S0 + 1, respectively as a function of wavenumber (k) along the width (designated by site index). The color bar shows the absolute scale of spin density.

Spin gap

To investigate the behaviour of spins in ZGNRs, we calculate the spin gap, Δs, which is the amount of energy required to flip one spin in the system. With decreasing Δs, the system becomes more subject to magnetic excitations. A zero spin gap refers to the degenerate magnetic ground state.

Figure 2c shows the Δs for half-filled ZGNRs of different widths over the BZ, obtained using the CAS-CI with 4900 basis states. With increasing width, the ZGNRs show gapless spin excitation over a larger region within k = π and the Dirac point. This behaviour is due to the increasing flat band region with increasing width, as we have described within the two-state model. Note that the appearance of a zero spin gap is unlikely for very narrow ribbons with only two or three zigzag chains, as evident from previous studies on spin ladders11,32. The difference in spin excitation behaviours for odd and even numbers of legs of spin ladders is not observed in our calculations33,34. This discrepancy can be attributed to the absence of backward scattering and umklapp scattering in our calculations. Nevertheless, we will present the systematic investigation of finite size systems, including these scattering processes, later in this article to validate our observations. Moreover, it has been observed that the spin gap progressively decreases with increasing width of the ladder. Therefore, we emphasise that our observations are robust in the case of wider ZGNRs.

The antiparallel alignment of spins within the opposite edges of ZGNRs8,13,21,35,36 remains unaltered within the many-body level of theory, due to the bipartite nature of the graphene lattice. As seen in Figure 2d, at k = π, the spins are completely localised in antiparallel fashion on the opposite edges for half-filled ZGNRs with Sztot = S0. However, a gapless spin excitation over the flat band region indicates that the state with Sztot = S0 + 1, which shows parallel spin orientation between opposite edges (see Fig. 2e), is degenerate to the antiferromagnetic ground state, as suggested by Lieb's theorem37. This observation suggests that once the complete ferromagnetic state is achieved by applying an external magnetic field, it persists as a stable state even after switching off the magnetic field in the case of undoped ZGNRs.

Hole doping

Now, let us investigate the magnetic and conducting properties of ZGNRs in the presence of holes. Our calculation indicates the reduction of charge and spin gaps upon hole doping, i.e., hole-induced metallic magnetism. Figure 3a shows the charge gap Δc variation with hole doping over the BZ for Nz = 20 ZGNR. The charge gap decreases drastically as the system moves away from the half-filled state, indicating a hole-induced transition towards the metallic phase. Note that the Δc for even and odd numbers of holes merge to two different values near the Dirac point, due to the systematic removal of electrons from the doubly occupied valence bands. However, this odd-even effect becomes indistinguishable for ZGNRs with larger widths when the charge gap for the hole-doped ZGNRs becomes negligibly small. Therefore, we observe a hole-mediated opening of conduction channels through the ZGNRs.

Figure 3. Charge gap and spin gap of hole-doped ZGNRs.

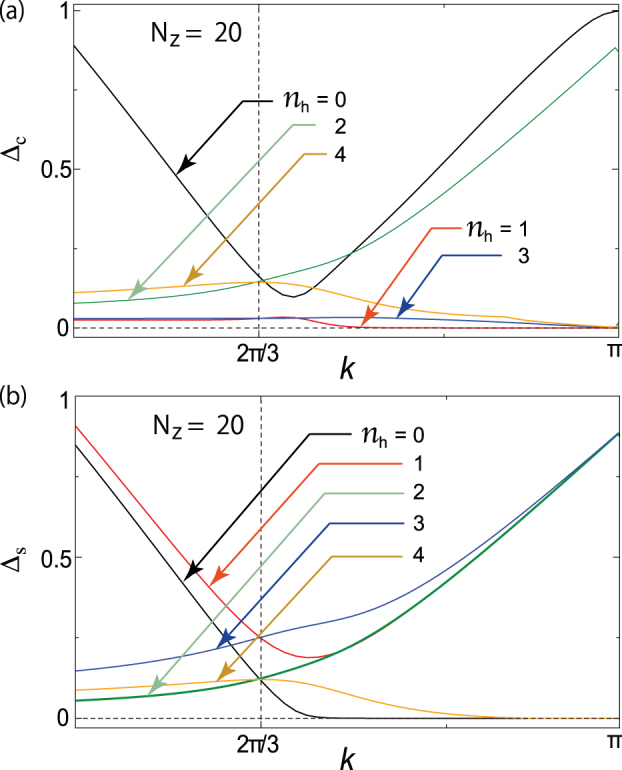
Figure 3

Open in a new tab

(a) The charge gap (Δc) and (b) spin gap (Δs) of ZGNR with Nz = 20 over k = π/2 → π for different hole (nh) doping.

Figure 3b shows the spin gap Δs for different hole dopings for Nz = 20 ZGNR. For single-hole doping, the spin needs to be excited from the band below the top of the valence band to the bottom of the conduction band. Therefore, the spin gap in this case is always higher than in the half-filled case, where the spin excitation comes from the top of the valence band. However, with increasing width, the closer spacing of the two top valence bands makes the spin gap for both cases almost equal over the k region from the BZ centre (k = 0) to the Dirac point. However, from the Dirac point to the BZ boundary, the Δs increases due to the appearance of edge states. The Δs for systems up to three-hole doping also shows a monotonic increase over this region, due to spin excitation to the top of the valence band, i.e., the edge state. The spin gap for these systems with up to three holes, however, decreases over the k region from the BZ centre to the Dirac point. Higher hole doping results in a gradual closing of the spin gap over the full BZ, and consequently, the system turns out to be magnetic. With increasing width, the Δs decreases without altering the qualitative behaviour. This decrease in the spin gap indicates hole-induced magnetism in ZGNRs. The observed odd-even effect in Δsalso becomes indistinguishable with increasing ZGNR width.

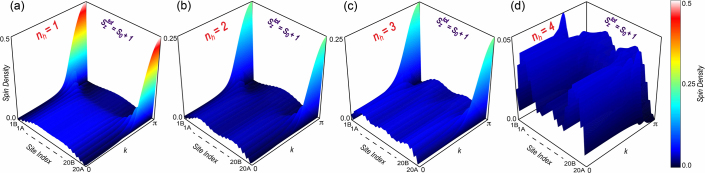
This appearance of magnetism drives us to explore the spin structure in ZGNRs with hole doping. Figure 4 shows the momentum-dependent spin density profile over the full BZ for an Nz = 20 ZGNR for the spin-excited state, i.e., Sztot = S0 + 1. With increasing hole doping, the spin-excited state of ZGNRs gradually stabilises and eventually turns out to be the ground state. The increase in width makes this process easier. As seen in the figure, the spin density mainly localises on the ZGNR edges at the BZ boundary for lower hole doping and gradually penetrates to the bulk sites as we move away from k = π. With increased hole doping, the absolute spin density on the edge atoms over the flat band region gradually decreases because of the systematic disappearance of electrons from the edge states. However, most importantly, all the remaining electrons align with the same spin orientation throughout the whole width, giving rise to a net magnetic moment for the hole-doped ZGNRs.

Figure 4. Spin density profile of hole-doped ZGNRs.

Figure 4

Open in a new tab

Spin density profile of hole doped ZGNR with Nz = 20 and Sztot = S0 + 1 as a function of wavenumber (k) along the width (designated by site index). The hole doping increases from left to right with (a) nh = 1, (b) nh = 2, (c) nh = 3 and (d) nh = 4. The color bar shows the absolute scale of spin density.

For further verification, in Figure 5, we plot the spin-spin correlation Inline graphic between two opposite-edge atoms (i and j) for a Nz = 20 ZGNR with Sztot = S0 over the full BZ for different dopings. At k = π, the half-filled ZGNR shows complete antiferromagnetic correlation between the two opposite edges, which decreases monotonically towards the Dirac point. We observe that the correlation within the bulk sites increases as k→2π/3 from its zero value at k = π and that in the vicinity of Dirac point, all the correlations within the bulk and edge sites become comparable.

Figure 5. Spin-spin correlation of ZGNRs.

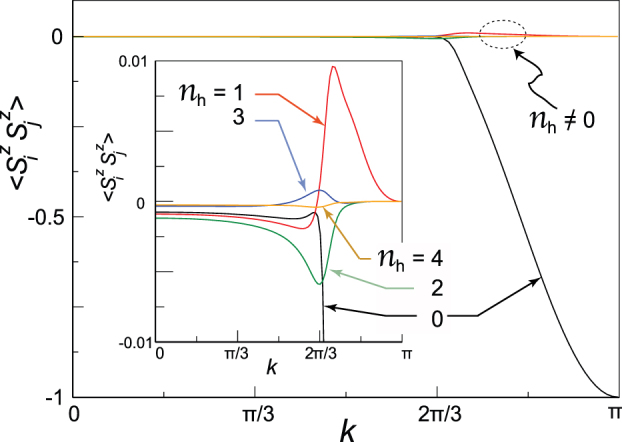
Figure 5

Open in a new tab

Spin-spin correlation between two opposite edge atoms of ZGNR with Nz = 20 over the BZ for different hole (nh) doping. The inset shows zoomed plot near 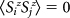Inline graphic.

The antiferromagnetic correlation between edges is largely destroyed by hole doping. Upon hole doping, electrons first vacate from the top of the valence band, i.e., the edge state, and hence, the spin density on the edge atoms vanishes gradually. In the case of an even number of holes, the spins disappear symmetrically from both the edges, but a system with an odd number of holes does not maintain a symmetrical spin distribution. Therefore, the spin-spin correlation shows an odd-even effect (see Fig. 5), though it is negligibly small due to quantum fluctuations. We observe that with hole doping, the antiferromagnetic correlation within two different sublattice points throughout the whole lattice also decreases over the full BZ. From the behaviour of the spin density profile and the spin-spin correlation, we can infer a hole-induced net magnetisation in ZGNRs.

Thus far, we have neglected the effect of scattering events connecting two different k-states to emphasise the simple and unified picture for the spin and charge excitation mechanism and their direct correspondence to the two-state model for ZGNRs. However, to investigate the effect of such scattering events, we perform the CAS-CI calculations for non-periodic finite size systems with long, smooth zigzag edges, which inherently include scattering processes arising from electronic correlations.

Figures 6a and 6b present the charge-gap and spin-gap behaviours, respectively, for such finite size systems as a function of inverse length (L), i.e., the number of unit cells for a fixed width, Nz = 6. Both Δc and Δs decrease upon hole doping, indicating conducting and magnetic behaviours, respectively, as we have already seen for periodic ZGNRs (see Fig. 3a and 3b). Interestingly, the very low value of Δseven in the case of the half-filled system (nh = 0) suggests an easily accessible magnetic state, as we have observed over the flat band region of periodic ZGNRs (see Fig. 2c).

Figure 6. Charge gap, spin gap and spin-spin correlation of finite size graphene and their response to hole doping.

Figure 6

Open in a new tab

(a) The charge gap (Δc) and (b) spin gap (Δs) for finite graphene system with long zigzag edge and fixed Nz = 6 as a function of inverse length (L), i.e., number of unit cells for different hole (nh) doping. (c) The spin-spin correlation 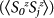Inline graphic, calculated from the “0” –th atom, located at the middle of the edge of the graphene structure with Nz = 6 (middle panel) with all the edge atoms (j) along the same edge (top panel) and with all the edge atoms (j) along the opposite edge (bottom panel) for different hole (nh) doping.

We also investigated the spin-spin correlation behaviour for finite size systems with different hole dopings. Figure 6c shows the spin-spin correlation calculated from one edge atom (the “0” –th site in the finite graphene structure, shown in the middle panel) with all other edge atoms along the same edge (top panel) and with all other edge atoms along the opposite edge (bottom panel). The ferromagnetic correlation (positive 〈S0zSjz〉) along the same edge decreases slowly with increasing hole doping because of the gradual disappearance of electrons from the edges, i.e., from edge states. The antiferromagnetic correlation (negative 〈S0zSjz〉) within the opposite edges shows a sharp decrease with hole doping, as observed in periodic ZGNRs (Fig. 5). All of these observations collectively lead us to the conclusion that the scattering events connecting different k-points in momentum space do not alter the qualitative outcome of our study for periodic ZGNRs.

Discussion

The observation of the magnetic ground state of ZGNRs, along with the decreased charge gap, suggests that hole-doped ZGNRs can act as magnetic conductors with an abundance of one type of spin in the charge carriers. This behaviour can be exploited to fabricate spin filters by controlling the background dielectric, as shown schematically in Figure 7. The hole doping can also be accomplished using oxidising agents that attract the electrons from the ZGNRs without destroying their backbone geometry. The originally antiferromagnetic and semiconducting ZGNRs (see Fig. 7a) can be turned into conducting spin filters by the application of gate bias (see Fig. 7b). However, although the device setup is rather conventional22,38,39,40,41,42,43, experimentally achieving magneto-transport requires the graphene channel to have smooth zigzag edges and the other perturbations such as substrate effect and electrode coupling to be minimised. In such an experimental situation, spin-dependent transport might be detected at low temperatures. From a theoretical viewpoint, the knowledge of scattering process and velocity of the charge carriers is also necessary for a complete understanding of spin-filtering behaviour. However, these issues are beyond the scope of the present study. Nevertheless, we look forward to further experimental and theoretical studies to realise this proposed experimental device setup. We are also pursuing transport calculations at the many-body level of theory in our follow-up studies.

Figure 7. Schematic representation of the possible application of ZGNRs.

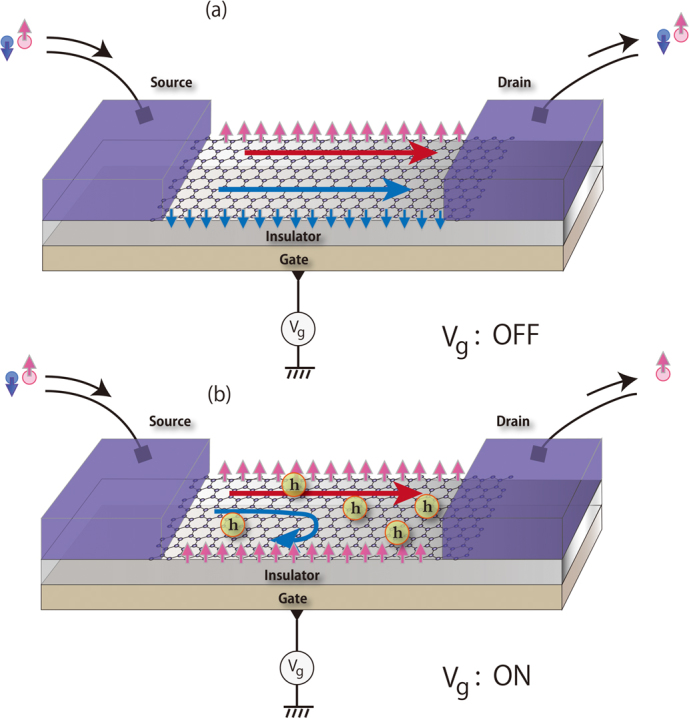
Figure 7

Open in a new tab

(a) The semiconducting and antiferromagnetic ground state of ZGNR with antiparallel spin orientation between opposite edges in absence of gate bias (Vg). (b) Hole doping due to the application of gate bias makes the ZGNR magnetic and conducting serving as spin filter.

To summarise, we have investigated the electronic properties of ZGNRs and their response to hole doping at the many-body CI level of calculations, taking into account the quantum fluctuations. The charge and spin excitation processes in ZGNRs have been explained based on an effective two-state model, which considers the top of the valence band and the bottom of the conduction band. Our study suggests that hole doping not only causes the ZGNRs to become conducting but also reduces the spin gap to make the ground state magnetic. This magnetism can be enhanced further by creating nano pores with zigzag edges in the bulk of the ZGNRs. These observations indicate the possibility of fabricating a spin-filter device based on ZGNRs by tuning the doping level. The fundamental understanding of the charge and spin excitation behaviours will guide further research in graphene and related materials and will provide tremendous impetus to the fascinating research area of carbon-based magnetism.

Methods

Because nanoscale materials contain a large number of atomic sites, it is very difficult to treat the electron-electron interactions properly. Although the mean field approach or the local density approximation (LDA) allows for a numerical solution of the Hubbard Hamiltonian even for sufficiently large widths, the one-electron description of electronic correlations suffers severely from the lack of representation of the quantum fluctuations. However, the many-body methods such as the density matrix renormalisation group and exact diagonalisation are not applicable for larger system sizes because of dimensionality limitations27.

In this paper, we employ the many-body configuration interaction (CI) method, which is widely known in quantum chemistry and has recently been used to investigate finite graphene quantum dots44,45. This multi-determinantal approach, built in molecular orbital space, provides excellent estimates of the ground and excited states46. To avoid the exploding size of the full-CI space with increasing width, we map the whole system into a complete active space (CAS) with the same number of valence and conduction bands around the Fermi energy at each k-point and consider all possible electron occupancies to construct the many-body basis. In our calculations, we consider 4 valence and 4 conduction bands around the Fermi energy. This choice gives 4,900 many-body basis states in CAS for the half-filled case with Sztot = 0. Note that in the case of periodic systems, the scattering processes within different k-points become crucial in determining the electronic or optical excitations. Although these scattering processes have been neglected in our study for simplicity, we confirm the qualitative observations by finite size calculations that inherently take into account such scattering events. The hole doping has been performed by the systematic removal of electrons from CAS at each k-point. This approach resembles the scattering process in angle-resolved photoemission spectroscopy (ARPES). With hole doping, the number of many-body basis states in CAS gradually decreases. Note that electron doping is expected to show simliar results, since the electron-hole symmetry is conserved in the nearest-neighbour Hubbard model.

Author Contributions

S.D. and K.W. performed the calculations, analyzed the results and wrote the paper.

Acknowledgments

S.D. acknowledges JSPS for postdoctoral fellowship and K.W. acknowledges the financial support by Grant-in-Aid for Scientific Research from the MEXT and the JSPS (Nos. 23310083, 20001006).

References

  1. Novoselov K. S. et al. Two-dimensional atomic crystals. Proc. Natl. Acad. Sci. 102, 10451–10453 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Novoselov K. S. et al. Two-dimensional gas of massless Dirac fermions in graphene. Nature 438, 197–200 (2005). [DOI] [PubMed] [Google Scholar]
  3. Zhang Y., Tan Y. W., Stormer H. L. & Kim P. Experimental observation of the quantum Hall effect and Berry's phase in graphene. Nature 438, 201–204 (2005). [DOI] [PubMed] [Google Scholar]
  4. Geim A. K. & Novoselov K. S. The rise of graphene. Nature Mater. 6, 183–191 (2007). [DOI] [PubMed] [Google Scholar]
  5. Ando T. Physics of graphene – zero-mode anomalies and roles of symmetry. Prog. Theo. Phys. Suppl. 176, 203–226 (2008). [Google Scholar]
  6. Castro Neto A. H., Guinea F., Peres N. M. R., Novoselov K. S. & Geim A. K. The electronic properties of graphene. Rev. Mod. Phys. 81, 109–162 (2009). [Google Scholar]
  7. Bae S. et al. Roll-to-roll production of 30-inch graphene films for transparent electrodes. Nature Nanotech. 5, 574–578 (2010). [DOI] [PubMed] [Google Scholar]
  8. Fujita M., Wakabayashi K., Nakada K. & Kusakabe K. Peculiar localized state at zigzag graphite edge. J. Phys. Soc. Jpn. 65, 1920–1923 (1996). [Google Scholar]
  9. Nakada K., Fujita M., Dresselhaus G. & Dresselhaus M. S. Edge state in graphene ribbons: nanometer size effect and edge shape dependence. Phys. Rev. B 54, 17954–17961 (1996). [DOI] [PubMed] [Google Scholar]
  10. Wakabayashi K., Fujita M., Ajiki H. & Sigrist M. Electronic and magnetic properties of nanographite ribbons. Phys. Rev. B 59, 8271–8282 (1999). [Google Scholar]
  11. Wakabayashi K., Sigrist M. & Fujita M. Spin wave mode of edge-localized magnetic states in nanographite zigzag ribbons. J. Phys. Soc. Jpn. 67, 2089–2093 (1998). [Google Scholar]
  12. Dutta S. & Pati S. K. Novel properties of graphene nanoribbons: a review. J. Mater. Chem. 20, 8207–8223 (2010). [Google Scholar]
  13. Wakabayashi K., Sasaki K. I., Nakanishi T. & Enoki T. Electronic states of graphene nanoribbons and analytical solutions. Sci. Tech. Adv. Mater. 11, 054504 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Wunsch B., Stauber T., Sols F. & Guinea F. Interactions and magnetism in graphene boundary states. Phys. Rev. Lett. 101, 036803 (2008). [DOI] [PubMed] [Google Scholar]
  15. Tao C. et al. Spatially resolving edge states of chiral graphene nanoribbons. Nature Phys. 7, 616–620 (2011). [Google Scholar]
  16. Mermin N. D. & Wagner H. Absence of ferromagnetism or antiferromagnetism in one- or two-dimensional isotropic Heisenberg models. Phys. Rev. Lett. 17, 1133–1136 (1966). [Google Scholar]
  17. Feldner H., Meng Z. Y., Lang T. C., Assaad F. F., Wessel S. & Honecker A. Dynamical signatures of edge-state magnetism on graphene nanoribbons. Phys. Rev. Lett. 106, 226401 (2011). [DOI] [PubMed] [Google Scholar]
  18. Dutta S. & Pati S. K. Half-metallicity in undoped and boron doped graphene nanoribbons in the presence of semilocal exchange-correlation interactions. J. Phys. Chem. B 112, 1333–1335 (2008). [DOI] [PubMed] [Google Scholar]
  19. Dutta S., Manna A. K. & Pati S. K. Intrinsic half-metallicity in modified graphene nanoribbons. Phys. Rev. Lett. 102, 096601 (2009). [DOI] [PubMed] [Google Scholar]
  20. Hod O., Barone V., Peralta J. & Scuseria G. E. Enhanced half-metallicity in edge-oxidized zigzag graphene nanoribbons. Nano. Lett. 7, 2295–2299 (2007). [DOI] [PubMed] [Google Scholar]
  21. Son Y. W., Cohen M. L. & Louie S. G. Energy gaps in graphene nanoribbons. Phys. Rev. Lett. 97, 216803 (2006). [DOI] [PubMed] [Google Scholar]
  22. Han M. Y., Oezyilmaz B., Zhang Y. & Kim P. Energy band-gap engineering of graphene nanoribbons. Phys. Rev. Lett. 98, 206805 (2007). [DOI] [PubMed] [Google Scholar]
  23. Jung J. & MacDonald A. H. Carrier density and magnetism in graphene zigzag nanoribbons. Phys. Rev. B 79, 235433 (2009). [Google Scholar]
  24. Swada K., Ishii F., Saito M., Okada S. & Kawai T. Phase control of graphene nanoribbon by carrier doping: appearance of noncollinear magnetism. Nano Lett. 9, 269–272 (2009). [DOI] [PubMed] [Google Scholar]
  25. Zhang Z., Chen C. & Guo W. Magnetoelectric effect in graphene nanoribbons on substrates via electric bias control of exchange splitting. Phys. Rev. Lett. 103, 187204 (2009). [DOI] [PubMed] [Google Scholar]
  26. Lieb E. H. & Wu F. Y. Absence of Mott transition in an exact solution of the short-range, one-band model in one dimension. Phys. Rev. Lett. 20, 1445–1448 (1968). [Google Scholar]
  27. Hikihara T., Hu X., Lin H. H. & Mou C. Y. Ground-state properties of nanographite systems with zigzag edges. Phys. Rev. B 68, 035432 (2003). [Google Scholar]
  28. Gebhard F. The Mott Metal-Insulator Transition (Springer-Verlag Berlin Heidelberg, 1997). [Google Scholar]
  29. Mielke A. Ferromagnetism in the Hubbard model on line graphs and further considerations. J. Phys. A 24, 3311 (1991). [Google Scholar]
  30. Mielke A. Exact ground states for the Hubbard model on the Kagome lattice. J. Phys. A 25, 4335 (1992). [Google Scholar]
  31. Zarea M., Busser C. & Sandler N. Unscreened Coulomb interactions and the quantum spin Hall phase in neutral zigzag graphene ribbons. Phys. Rev. Lett. 101, 196804 (2008). [DOI] [PubMed] [Google Scholar]
  32. Gopalan S., Rice T. M. & Sigrist M. Spin ladders with spin gaps: a description of a class of cuprates. Phys. Rev. B 49, 8901–8910 (1994). [DOI] [PubMed] [Google Scholar]
  33. Yoshioka H. Spin excitation in nano-graphite ribbons with zigzag edges. J. Phys. Soc. Jpn. 72, 2145–2148 (2003). [Google Scholar]
  34. Dagotto E. & Rice T. M. Surprises on the way from one- to two-dimensional quantum magnets: the ladder materials. Science 271, 618–623 (1996). [Google Scholar]
  35. Kobayashi Y., Fukui K. I., Enoki T., Kusakabe K. & Kaburagi Y. Observation of zigzag and armchair edges of graphite using scanning tunneling microscopy and spectroscopy. Phys. Rev. B 71, 193406 (2005). [Google Scholar]
  36. Kobayashi Y., Fukui K. I., Enoki T. & Kusakabe K. Edge-state on hydrogen-terminated graphite edges investigated by scanning tunneling microscopy. Phys. Rev. B 73, 125415 (2006). [Google Scholar]
  37. Lieb E. H. Two theorems on the Hubbard model. Phys. Rev. Lett. 62, 1201–1204 (1989). [DOI] [PubMed] [Google Scholar]
  38. Stampfer C., Guttinger J., Molitor F., Graf D., Ihn T. & Ensslin K. Tunable Coulomb blockade in nanostructured graphene. Appl. Phys. Lett. 92, 012102 (2008). [Google Scholar]
  39. Stampfer C., Schurtenberger E., Molitor F., Guttinger J., Ihn T. & Ensslin K. Tunable graphene single electron transistor. Nano Lett. 8, 2378–2383 (2008). [DOI] [PubMed] [Google Scholar]
  40. Guttinger J. et al. Electron-hole crossover in graphene quantum dots. Phys. Rev. Lett. 103, 046810 (2009). [DOI] [PubMed] [Google Scholar]
  41. Stampfer C., Guttinger J., Hellmuller S., Molitor F., Ensslin K. & Ihn T. Energy gaps in etched graphene nanoribbons. Phys. Rev. Lett. 102, 056403 (2009). [DOI] [PubMed] [Google Scholar]
  42. Todd K., Chou H. T., Amasha S. & Goldhaber-Gordon D. Quantum dot behavior in graphene nanoconstrictions. Nano Lett. 9, 416–421 (2009). [DOI] [PubMed] [Google Scholar]
  43. Han M. Y., Brant J. C. & Kim P. Electron transport in disordered graphene nanoribbons. Phys. Rev. Lett. 104, 056801 (2010). [DOI] [PubMed] [Google Scholar]
  44. Dutta S., Lakshmi S. & Pati S. K. Electron-electron interactions on the edge states of graphene: a many-body configuration interaction study. Phys. Rev. B 77, 073412 (2008). [Google Scholar]
  45. Guclu A. D., Potasz P., Voznyy O., Korkusinski M. & Hawrylak P. Magnetism and correlations in fractionally filled degenerate shells of graphene quantum dots. Phys. Rev. Lett. 103, 246805 (2009). [DOI] [PubMed] [Google Scholar]
  46. Szabo A. & Ostlund N. S. Modern Quantum Chemistry (McGraw-Hill, New York, 1989). [Google Scholar]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES