Figure 1.

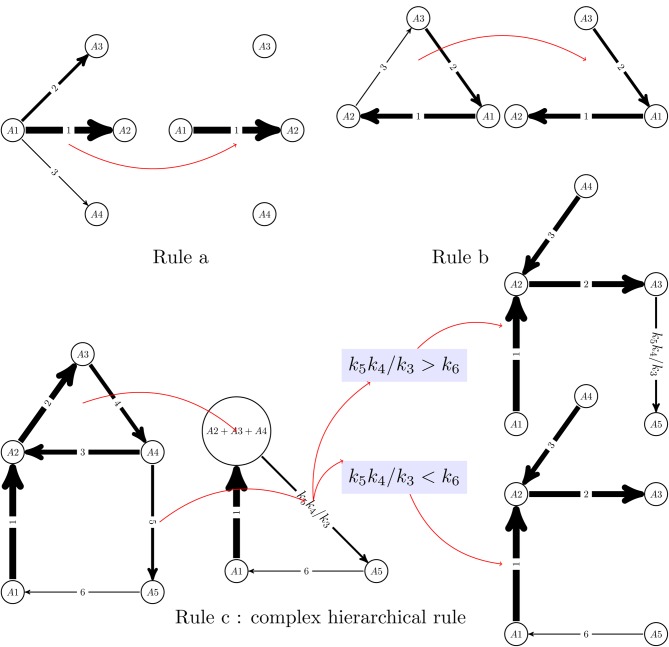
Reduction algorithm for linear networks. A monomolecular network with total separation can be represented as a digraph with integer labels (the quickest reaction has label 1). Two simple rules allow to eliminate competition between reactions (rule a) and transform cycles into chains (rule b). Rule b can not be applied to cycles with outgoing slow reactions, in which case more complex, hierarchical rules should be applied (rule c). In the rule c, first the cycle A₂ → A₃ → A₄ → A₂ is “glued” to a new node (pool A₂+ A₃+ A₄) and the constant of the slow outgoing reaction renormalized to a monomial k₅k₄/k₃. Rule b is applied to the resulting network, which is a cycle with no outgoing reactions. The comparison of the constants k₅k₄/k₃ and k₆ dictates where this cycle is cut. Finally, the glued cycle is restored, with its slowest step removed.