The algorithm is schematically described in Figure 1.
Input:
A ranked list of sequences S1, … , SN
Parameters 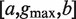 where a represents the length of the first half site, b represents the length of the second half site and 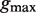 represents the maximum gap.
P-value threshold for reporting (τ)
Output:
A list of sequence motifs of the form H1-NΛ-H2, where Λ is a set of gaps. These reported motifs are rank imbalanced in S1, … , SN at an mHG significance level better than τ. /* The interpretation of the above motif representation is as follows. A motif is viewed as a set of strings. In this case all strings that start with H1, then have a wildcard gap of any of the lengths in the set of gaps Λ, and end with H2. For example, the motif GCC-N1,5-ATG represents the strings GCCNATG and GCCN5ATG */
|
Preprocessing:
Construct a generalized suffix tree for S1, … , SN such that:
All suffixes of all sequences S1, … , SN are represented by paths from the root to leaves in the tree. Each leaf contains information about the occurrences of the corresponding suffix w in S1, … , SN. This information is represented as a list m1(w), … , mN(w)(w), where mi(w) are the indices, amongst 1, … , N, of the sequences at which w occurs.
/* The construction is implemented using Ukkonen's algorithm ( 41) */
|
Algorithm:
Traverse the tree to find paths of length a, and for each path P do:
Compute the set of all strings σ 1( P), … , σ N(P)( P) of length 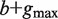 that start at the position where P ends in all sequences among S1, … , SN in which it occurs. This step is implemented by traversing the subtree rooted at P. /* The strings σ i( P) are typically of length 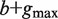 . When P occurs close to the end of Si, a string of length smaller than 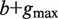 is taken into the above set */ Construct a generalized suffix tree T( P) for σ 1( P), … , σ N(P)( P) such that:
Traverse T( P) at depth b. For each such path Q calculate the enrichment of all possible motifs of the form P- NΛ- Q, where Λ is any subset of 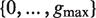 , using the following process: /* This step uses the suffix tree information to avoid searching over all 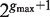 possible instantiations of Λ, leading to improved efficiency of the algorithm */
|