Skip to main content
. 2012 Jul 25;3:245. doi: 10.3389/fpsyg.2012.00245

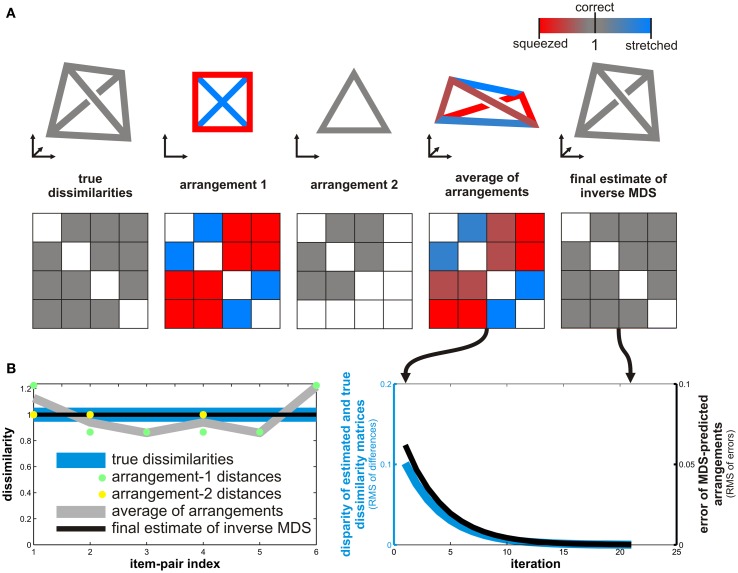
Figure 3.

Figure 3

Inverse MDS by iterative algorithm. Inverse MDS estimates a higher-dimensional RDM from multiple low-dimensional arrangements. (A) In this toy example, we have four items and the dissimilarities are equal for all six pairs (all dissimilarities are 1), forming a tetrahedron in 3D (top left, RDM underneath in middle row). Arrangements are in 2D. We use MDS (optimizing metric stress) to simulate a subject’s arrangements. Arrangement 1 (second from left in top row) contains all four items. As the four items are optimally arranged in 2D, distances are squeezed and stretched (red and blue connections and RDM cells, respectively). Arrangement 2 (third from left in top row) contains only three of the four items. The three items’ RDM is perfectly represented by the 2D arrangement. A simple way to estimate the underlying RDM is to average the distance matrices of the 2D arrangements (second from right in top). Missing dissimilarity entries are ignored in the averaging and the matrices are first separately normalized by scaling the dissimilarities’ root mean square for the defined entries to the same value. (B) Results of iterative inverse MDS for the toy problem. The aligned-average RDM (gray line in left panel) is a better estimate of the true dissimilarities (blue line) than the distance matrix of arrangement 1 (green dots), but distortions remain. Inverse MDS can be performed by starting from the aligned-average matrix and iteratively improving the estimate. On each iteration, the current estimate is used to predict the subject’s arrangements by MDS. The disparities between the predicted and the actual arrangements are then used to adjust the estimate of the underlying RDM. The resulting iterative reduction of the error of the MDS-predicted arrangements (black line in right panel) reduces the disparity between the true and the estimated dissimilarity matrices (blue line in right panel; disparity measured as root mean square of differences after normalization of both matrices). In this toy example, the two arrangements shown suffice to perfectly recover the tetrahedral true RDM (black line in left panel).