Introducing the At-Risk Average Causal Effect with Application to HealthWise South Africa

Abstract

Researchers often hypothesize that a causal variable, whether randomly assigned or not, has an effect on an outcome behavior and that this effect may vary across levels of initial risk of engaging in the outcome behavior. In this paper, we propose a method for quantifying initial risk status. We then illustrate the use of this risk-status variable as a moderator of the causal effect of leisure boredom, a non-randomized continuous variable, on cigarette smoking initiation. The data come from the HealthWise South Africa study. We define the causal effects using marginal structural models and estimate the causal effects using inverse propensity weights. Indeed, we found leisure boredom had a differential causal effect on smoking initiation across different risk statuses. The proposed method may be useful for prevention scientists evaluating causal effects that may vary across levels of initial risk.

Often researchers hypothesize that a variable has a causal effect on an outcome behavior, and that this effect varies across levels of risk of engaging in the outcome behavior. In other words, risk status is a moderating variable. For example, universal prevention programs often have small effects, which may be due to the intervention being applied to those who do not need it. In a universal sample, there are likely to be individuals who would not take up the risky target behavior regardless of whether or not they receive the intervention. These individuals are either not at-risk or have a low risk for engaging in the target behavior. Similarly, there are likely to be individuals who would take up the target behavior regardless of whether they receive the intervention or not. In either case, the intervention does not have an effect for these individuals. Thus, it is possible that the intervention has much larger effects for particular subgroups of risk status than it does when averaged across all participants in the study.

As another example, researchers may be interested in identifying a potential mediator (e.g., leisure boredom) so that they can design an intervention to target the mediator. If the potential mediator does not have a causal effect on the outcome, then it would not make sense to design an intervention to change it. This effect is often referred to as “conceptual” theory (MacKinnon 2008). In this case, the potential mediator is the hypothesized cause or exposure variable, and the causal effect of it may vary over levels of initial risk for engaging in the behavior.

This paper illustrates a method based on the potential outcomes framework for causal inference to estimate the effect of a hypothesized cause, leisure boredom, on smoking initiation and incorporating initial risk status as a moderator. We refer to this as the at-risk average causal effect (ACE). The idea of estimating an at-risk ACE is not limited to this specific application. Rather, it applies to estimating the causal effect of any hypothesized causal variable. The HealthWise South Africa study, a longitudinal study of adolescent risk behaviors in Cape Town, South Africa, provides a substantive application of the methods associated with estimating the at-risk ACE and the potential outcomes framework for causal inference.

Application: HealthWise South Africa

HealthWise South Africa is a collaborative effort between faculty members at Pennsylvania State University, University of the Western Cape, and University of Cape Town aimed at reducing youth risk behaviors (see Caldwell et al. 2004 for details). Four high schools implemented the HealthWise intervention and five high schools served as the control group. We use only the control group (N= 1,414; 49% male) for this analysis. All schools were in the Mitchell’s Plain area of Cape Town, South Africa, which is a low-income, predominantly mixed race (a.k.a., Colored, derived from Asian, European, and African ancestry) township established during the Apartheid era. Most participants identified themselves as Colored (90%), with the remaining students identifying as Black (6%) or White (4%). Assessments were conducted at the beginning and end of each school year, starting in the 8th grade (M age = 13.98). The first assessment will be referred to as baseline. At the end of that school year, the first post-intervention assessment was conducted and it will be referred to as 6-month follow-up. Finally, at the beginning of ninth grade, 1 year after the baseline assessment, the second post-intervention assessment was conducted and it will be referred to as 1-year follow-up.

Using HealthWise as an example, we will estimate the at-risk ACE. In this example, our goal is to estimate the causal effect of leisure boredom on smoking initiation. Thus, we address the following substantive research question: What is the effect of boredom with leisure activities on initiation of cigarette smoking by the 1-year follow-up, for different levels of baseline risk for smoking?

Leisure boredom was measured with a 5-point Likert-type response option where 0 = strongly disagree and 4 = strongly agree. The mean of the following items was computed at each measurement occasion: “For me, free time just drags on and on,” “Free time is boring,” and “I usually don’t like what I’m doing in my free time, but I don’t know what else to do.” Finally, because the measurement scale for leisure boredom is not inherently meaningful, we mean-centered the composite leisure boredom variable such that 0 represents a mean level of leisure boredom. The outcome, cigarette smoking, was measured by one item: “How many cigarettes have you smoked in your entire life?” Response options were 0 = none or a few puffs and 1 = 1 or more cigarettes.

Individuals were not randomly assigned to levels of leisure boredom and therefore there may be confounders which bias the estimate of the causal effect if they are not properly accounted for. Confounders are variables that influence both leisure boredom and smoking initiation and they should be accounted for when estimating the causal effect. We will describe below how we account for potential confounders but first we will describe how we defined the moderator variable, initial risk status.

Defining Risk Status

We constructed the at-risk variable by predicting smoking at baseline using the following covariates in a logistic regression model: dummy variables for gender and school; whether the family owned an automobile; participation in sports or physical activities, singing, drama, dance, or playing a musical instrument during the past 4 weeks; time spent doing hobbies, creative activities, volunteer work, or going to a park or community center during the past 4 weeks; confidence about avoiding risky situations and identifying when situations might turn risky; knowledge of where to get help if someone was pushing them to use drugs; confidence that they could successfully resolve a conflict and how important they believe it is to resolve conflicts peacefully; leisure boredom, healthy leisure attitudes, new interests in leisure activities, and management of anxiety and anger.

From the logistic regression model, we obtained the predicted probabilities for having smoked by baseline. This model is referred to as the at-risk model. This at-risk model does not attempt to infer that any of the predictors in the at-risk model cause cigarette smoking. The goal of the at-risk model is to obtain an accurate predicted probability of initial smoking status, which we considered the initial risk of smoking.

For the subsequent analysis, we created four strata based on quartiles of the distribution of predicted probabilities and created dummy variables for membership in each of the strata. The 25th percentile of the distribution was .24, the 50th percentile was .33, and the 75th percentile was .45. The lowest predicted probability of smoking initiation was .06 and the highest was .80. The mean predicted probability was .35. The strata with the lowest probabilities of smoking will be referred to as the low-risk status and the strata with the highest probabilities of smoking will be referred to as the high-risk status. The two intermediate strata will be referred to as the medium-low risk status and the medium-high risk status. It is not necessary that the at-risk variable be treated as nominal, but because we will treat boredom as continuous, it is much easier to interpret the interaction effect later in the HealthWise example if both variables are not continuous.

The entire sample was used in defining the at-risk variable. However, once we defined the at-risk variable, we limited further analysis to those who had not smoked by the 6-month follow-up (N=562) because we are interested in smoking initiation by the 1-year follow-up. In other words, further analysis is limited to individuals who had varying risk for having smoked at baseline, but none who had already smoked at baseline or the 6-month follow-up. Thus, we are careful to define the causal effect, which we will do formally below, such that the outcome occurs after leisure boredom.

Next we will describe the potential outcomes framework, the marginal structural model (MSM), and estimation of the causal effects. Finally, we will return to the example described previously and illustrate the analysis using the HealthWise data.

Potential Outcomes Framework

Much work in causal inference derives from the potential outcomes framework (Rubin 1974, 2005) in which each individual has a potential outcome under every possible level of the hypothesized causal variable. For ease of explanation, consider for the moment a binary “treatment” or exposure. For example, suppose that individuals may have a high or low level of leisure boredom. In this case, there is a potential outcome for each participant under a high level and a low level. Let B_i denote the level for participant i, i =1,…, n. Those with B_i=1 have a high level of leisure boredom, and those with B_i =0 have a low level. Let Y_i(1) be the potential outcome if B_i=1, and Y_i(0) be the potential outcome if B_i=0. For those individuals with a low level of leisure boredom, the potential outcomes under the high level, Y_i(1), are missing. Likewise, for those individuals with a high level of leisure boredom, the potential outcomes under the low level, Y_i(0), are missing. The missing potential outcome is often referred to as the counterfactual outcome because it is what would have happened if the individual had been exposed to the other level. The causal effect for participant i, defined as Y_i(1)–Y_i(0), cannot be observed because one of the two potential outcomes is missing for any given individual. Randomized studies ensure that the missing potential outcome is missing completely at random (MCAR; Little and Rubin 2002; Schafer 1997). Under the MCAR assumption, the ACE may be estimated from the observed data and is unbiased. Without random assignment, we cannot assume that the missing potential outcome is MCAR. In this case, estimation of causal effects from the observed data will generally be biased even if there is no other missing data. For non-randomized studies, strategies have been implemented to estimate the ACE, which is the causal effect averaged over participants in the study, defined as E[Y_i(1)–Y_i(0)]. Schafer and Kang (2008) provide an introduction to many of these strategies. The above notation may be expanded to consider continuous hypothesized causal variables, in which case each individual has potential outcomes under each level of the hypothesized causal variable, resulting in a function (Imbens 2000).

The notation above for the potential outcomes framework implies that there is no interference among individuals because the potential outcomes, Y_i(B_i), are written as a function of B_i and not B_j where i and j denote two different individuals. That is, one individual’s outcome does not depend on another individual’s level of leisure boredom. If it does, then the notation must be expanded (e.g., Y_i(B_i, B_j)). Thus, a nested or multilevel data structure may violate this no-interference assumption. Throughout this article, we make this no-interference assumption. Methods have appeared in the statistics literature for situations in which this assumption does not hold (e.g., Hong and Raudenbush 2005, 2006). The above notation also relies on what is usually referred to as the consistency assumption. The assumption states that if an individual has a high level of boredom, then the outcome that is observed, denoted Y_i, is Y_i(1). Likewise, if an individual has a low level of boredom, then the outcome that is observed is Y_i(0).

Within the potential outcomes framework, a variety of methods have been proposed for defining and estimating the ACE. We will use marginal structural models (MSMs; Robins et al. 2000) to define the causal effects of interest and inverse propensity weights (IPW) to estimate those effects. For simplicity, we have dropped the subscript i for individuals for the remainder of the manuscript.

Marginal Structural Models

MSMs are used to define the causal effects of interest in terms of potential outcomes. They can be any type of model, such as a logistic regression model, a survival analysis model, or a linear regression model. The key is that they are written in terms of potential rather than observed outcomes. Thus, for our research question, the MSM is given as

$$E[Y(b)\mid Z]={\beta }_0+{\beta }_{1}b+{\beta }_2{D}_2+{\beta }_3{D}_3+{\beta }_4{D}_4+{\beta }_5{D}_{2}b+{\beta }_6{D}_{3}b+{\beta }_7{D}_{4}b,$$

where D represents a dummy variable indicating level of initial risk and b represents a specific level of leisure boredom. The low-risk status is the reference. D₂ =1 if the individual is in the medium-low risk status and 0 otherwise, D₃ =1 if the individual is in the medium-high risk status and 0 otherwise, and D₄ =1 if the individual is in the high risk status and 0 otherwise. Using the MSM, we can define various causal effects of leisure boredom on smoking initiation at 1-year follow-up if we chose two specific levels of boredom (e.g., b and b′) and a value for Z. The moderator variable, risk status, is denoted Z and Z=1 refers to the low-risk strata, Z=2 refers to the medium-low risk strata, Z=3 refers to the medium-high risk strata, and Z=4 refers to the high-risk strata, defined by quartiles as described previously. For example, if we wish to define the causal effect of a mean level of boredom versus a level of boredom one standard deviation above the mean given the low risk status, then the causal effect is

$$E[Y(.94)-Y(0)\mid Z=1]=[{\beta }_0+{\beta }_1(.94)]-{\beta }_0={\beta }_1(.94).$$

Recall that boredom is centered at the mean. The standard deviation of leisure boredom is 0.94. Specific values could also be chosen to represent the causal effect of a one-unit change in boredom. These MSMs can be written for defining the causal effect of a mean level of boredom versus a level of boredom one standard deviation above the mean given the medium-low risk status, the medium-high risk status, and the high risk status, respectively:

$$\begin{array}{l}E[Y(.94)-Y(0)\mid Z=2]=[({\beta }_0+{\beta }_2)+({\beta }_1+{\beta }_5)(.94)]-[{\beta }_0+{\beta }_2]=({\beta }_1+{\beta }_5)(.94),\\ E[Y(.94)-Y(0)\mid Z=3]=[({\beta }_0+{\beta }_2)+({\beta }_1+{\beta }_6)(.94)]-[{\beta }_0+{\beta }_2]=({\beta }_1+{\beta }_6)(.94),\\ E[Y(.94)-Y(0)\mid Z=4]=[({\beta }_0+{\beta }_2)+({\beta }_1+{\beta }_7)(.94)]-[{\beta }_0+{\beta }_2]=({\beta }_1+{\beta }_7)(.94).\end{array}$$

We can also define the causal effect of a level of boredom one standard deviation below the mean versus a mean level of boredom on smoking initiation given the low-risk status,

$$E[Y(-.94)-Y(0)\mid Z=1]=[{\beta }_0+{\beta }_1(-.94)]-{\beta }_0={\beta }_1(-.94)$$

and likewise for the medium-low, medium-high, and high-risk statuses.

Inverse Propensity Weighting

MSMs are typically estimated using IPWs, although other estimators are available (e.g., van der Wal et al. 2009). IPW uses propensity scores, which will be briefly described before we discuss the creation of weights.

Propensity Scores

Rosenbaum and Rubin (1983) defined the propensity score as the probability that an individual receives a particular level of the hypothesized causal variable given measured confounders, denoted X. These confounders are variables that take on their values before the hypothesized causal variable and thus cannot be affected by it. Confounders may also include unchangeable characteristics (e.g., gender) that may be statistically related to Y. When the hypothesized causal variable is binary, propensity scores are typically estimated by fitting a logistic regression model of the hypothesized causal variable on X in the sample data. In this case, the predicted probabilities from the logistic regression model are estimates of the propensity scores (π̂). Suppose that leisure boredom were binary; then, individuals with high and low levels of leisure boredom with identical propensity scores would have identical distributions for all of the confounders included in the propensity model. Therefore, they could be divided into groups with similar propensity scores and then treated as if they had participated in a randomized experiment.

If the treatment is continuous, which is actually the case for leisure boredom, then the generalized propensity score may be obtained from the probability density function (p.d.f.) of leisure boredom given the measured confounders, φ(B|X), (Hirano and Imbens 2004; Imai and van Dyk 2004). These are obtained by a linear regression of B on X and a probability is obtained by inserting the fitted values from the regression, denoted b̂; in the normal p.d.f. (denoted φ()),

$$\phi (b)=\frac{1}{\sqrt{2\pi {\widehat{\sigma }}^2}}{e}^{-\frac{{\left(b-\widehat{b}\right)}^2}{2{\widehat{\sigma }}^2}},$$

where σ̂ is the residual standard error from the regression of B on X. Note that the π in this equation is the constant (i.e., 3.14). Stated differently, the standardized residuals are obtained from a regression of B on X and the propensity score is the probability of the standardized residuals under a normal distribution; that is, the probability of receiving a particular level of boredom given measured confounders.

We will estimate generalized propensity scores, create weights based on them, and use IPW to estimate the causal effects defined by the MSMs given above.

Creating the Weights

IPW is similar to survey sampling weights where the weights are the inverse probability of being sampled. Again, suppose for a moment that leisure boredom were binary. Participants with a high level of leisure boredom would be given a weight of 1/π̂ and participants with a low level of leisure boredom would be given a weight of 1/(1 − π̂), because π̂ is the propensity of having a high level of leisure boredom. Thus, the propensity of having a low level of leisure boredom is (1 − π̂). In other words, the weight for an individual is the inverse of the propensity for being in the level that the individual is actually in. When there is a baseline moderator, Z, the weights include it in both the numerator and denominator models. The denominator model also includes measured confounders. For those in the high level of boredom, the model for the numerator of the weights would be P[B=1|Z] and the model for the denominator of the weights would be P[B=1|X, Z]. Similarly, for those in a low level of boredom, the models for the numerator and denominator of the weights would be 1–P[B=1|Z] and 1–P[B=1|X, Z], respectively.

When the hypothesized causal variable is continuous, weights should always be stabilized regardless of the presence or absence of a moderator (Robins et al. 2000). The numerator probability of the stabilized weights is given by the p.d.f., φ(B), of an “empty” or intercept-only regression model. The stabilized weights are then given by a ratio of the p.d.f.s for the numerator and denominator models (i.e., φ(B)/φ(B|X)). The reason for stabilizing the weights is that if the confounders had no influence on selection into levels of leisure boredom, the φ(B|X)would be equal to φ(B), which means that the weight for that individual would be 1 (see Robins et al. 2000). If a moderator is of interest, it would be included in both the numerator and denominator models. When using stabilized weights, the mean of the weights should be approximately one. For further details about creating weights and the numerator and denominator models for the weights, see Cole and Hernan (2008).

Once the weights have been created, then they are incorporated into the MSM in the same manner as survey weights. The implementation of the weights will be illustrated below using the survey package for R (Lumley 2010). Assuming that all confounders have been included in the denominator model for the weights, the MSM needs only to include the hypothesized causal variable, the moderator variable, and their interaction. In our example, the moderator variable is treated as a nominal variable; thus, there are three dummy variables and interactions between leisure boredom and each of these dummy variables. For example, for the HealthWise application, the following model will be fit to the observed data using IPW:

$$P[Y=1\mid B=b,Z=z]={\beta }_0+{\beta }_{1}b+{\beta }_2{D}_2+{\beta }_3{D}_3+{\beta }_4{D}_4+{\beta }_5{D}_{2}b+{\beta }_6{D}_{3}b+{\beta }_7{D}_{4}b,$$

where Z is initial risk status, Y is cigarette smoking, and B is leisure boredom.

The critical assumption upon which IPW (and other propensity score methods) relies is known as ignorability or unconfoundness. This assumption states that all confounders are measured; that is, there are no unmeasured confounders, which is impossible to verify. However, the assumption becomes more plausible as more potential confounders are included. It should be noted that ANCOVA or regression adjustment requires this assumption as well. An advantage of propensity score methods over regression adjustment is that the propensity score is a single number summary of a potentially large number of confounders and including all of these confounders as covariates in a regression model would be impractical.

Statistical Analysis of HealthWise Data

As is often the case in practice, there are missing data dispersed throughout the HealthWise data set due to skipped items or school absences. Therefore, we began by multiply imputing five complete data sets. In the imputation model, we included all of the variables that were potential confounders in the propensity model, the at-risk model, or the outcome model so that the imputation model was more general. For each imputation, we fit the at-risk model and the propensity model, created the weights, and estimated the causal effects using IPW. Finally, we averaged the causal effect estimates across the five imputations using Rubin’s rules (Little and Rubin 2002; Schafer 1997). We used five imputed data sets because generally five imputations have been shown to be sufficient (see Schafer 1997).

A propensity model for the denominator of the weights for leisure boredom was fitted using the following covariates: dummy variables for gender, religion, and school; risk status; participation in sports or physical activities, singing, drama, dance, or playing a musical instrument during the past 4 weeks; time spent doing hobbies, creative activities, volunteer work, or going to a park or community center during the past 4 weeks; and knowledge of where to go to play sports, get help with school work, or have fun; and healthy leisure attitudes. The denominator propensity model also included items which measured (a) free time self-efficacy, (b) development of new interests in the previous 6 months, (c) free time motivations, (d) parental control over free time activities, (e) parental support for autonomy over free time activities, and (f) whether the participant’s family owned an automobile. The moderator, risk status, is included in both the numerator and denominator propensity models. The propensity models were fit using linear regression models in R. The predicted probabilites for both the numerator and denominator models are obtained as described previously, using the normal p.d.f. and the stabilized weights were constructed as described above. The mean of the stabilized weights was 1.01. The R code and equivalent SAS code for the analysis is given in the Appendix.

Results

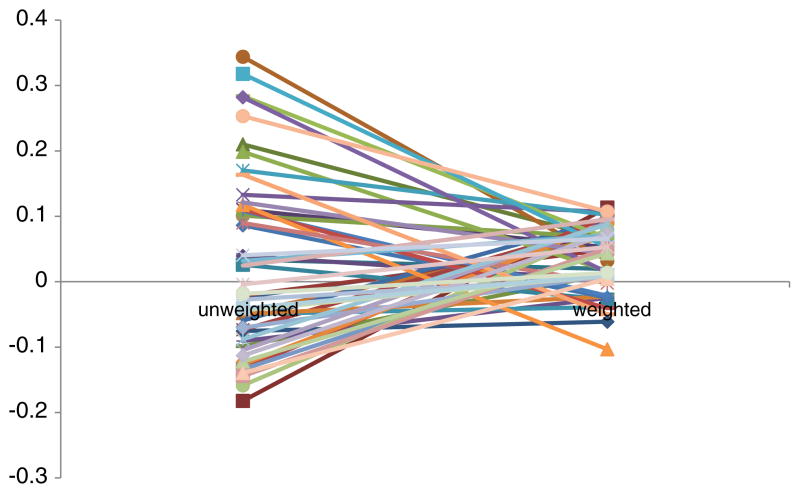
First, we assessed the balance on the measured confounders before and after weighting. Figure 1 shows the correlations between leisure boredom and each of the measured confounders prior to weighting (left hand side) and after weighting (right hand side). Each point represents a correlation and the correlation before and after weighting for the same confounder is connected by a line. This type of figure is an easy way to illustrate that prior to weighting, many correlations were above 0.1 (considered a small correlation by Cohen 1988) but that after weighting, the correlations were less than 0.1. In other words, all the correlations were “small” in the weighted data. Next, we present the results for the outcome analysis.

Fig. 1.

Correlations between leisure boredom and each confounder before and after weighting

Because smoking at 1-year follow-up was binary, the outcome model was a logistic regression. An alpha level of .05 was used for all statistical tests. The estimates, standard errors, and p-values, averaged across the five imputed data sets, are presented in Table 1.

Table 1.

Parameter estimates, standard errors, and p-values (averaged across the five imputed data sets) for the effect of leisure boredom on initiating cigarette smoking by 1-year follow-up among risk statuses

	Estimate	Std. error	p-value
Intercept	−2.53	0.28	<.001
Bored	0.75	0.27	.005
D2	0.99	0.35	.005
D3	0.84	0.41	.039
D4	1.33	0.53	.012
D2*bored	0.93	0.34	.006
D3*bored	−0.37	0.52	.475
D4*bored	−0.77	0.47	.106

Because the low-risk status is the reference, β₁ represents the effect of leisure boredom on smoking initiation in the low risk status. The effect of leisure boredom on smoking initiation in the medium-low risk status is β₁+ β₅. Likewise, the effect of leisure boredom on smoking initiation in the medium-high risk status is β₁+ β₆, and the effect of leisure boredom on smoking initation in the high-risk status is β₁ + β₇. The effect of leisure boredom on smoking initiation is statistically significant in the low- and medium-low risk statuses and is not significant in the medium-high and high-risk statuses (see Table 1).

For the causal effects defined above, we found that those at one standard deviation above the mean level of boredom are two times more likely to initiate smoking at the 1-year follow-up than those at the mean, given the low-risk status. Those at one standard deviation below the mean are 51% less likely to initiate smoking than those at the mean given the low-risk status. Those at one standard deviation above the mean have 1.18 greater odds of initiating smoking than those at the mean, given a medium-low risk status. Those at one standard deviation below the mean are 15% less likely to initiate smoking than those at the mean, given a medium-low risk status. Those at one standard deviation above the mean are 1.43 times more likely to initiate smoking than those at the mean, given a medium-high risk status. Those at one standard deviation below the mean are 30% less likely to initiate smoking than those at the mean, given a medium-high risk status. Finally, given the high-risk status, those at one standard deviation above the mean or one standard deviation below the mean were not more likely to initiate smoking than those at the mean.

Table 2 presents the predicted probability of smoking initiation given risk status for the mean level of leisure boredom and for one standard deviation above and below the mean. As shown in Table 2, the predicted probability of smoking increases when moving from the top to the bottom of the table and when moving from left to right. In other words, the predicted probability of smoking initiation generally (the medium-low risk status is the exception) increases as risk status increases and as boredom increases.

Table 2.

Predicted probabilities of smoking initiation by 1-year follow-up

	−1 SD = −.94	Mean boredom	+1 SD = .94
Low risk	.037	.074	.140
Medium-low risk	.147	.177	.201
Medium-high risk	.114	.156	.210
High risk	.233	.231	.228

Note that when we added the risk status variable as an ordinal rather than a nominal variable, we obtained the same conclusions. An increase in leisure boredom had a statistically significant effect on cigarette smoking initation by the 1-year follow-up, such that an increase in leisure boredom resulted in an increase in the odds of smoking. As expected, there was a statistically significant effect of risk status on smoking initiation. The interaction between leisure boredom and risk status was statistically significant. The interaction effect was such that the increased probability of smoking initiation due to increased leisure boredom decreases (i.e., the effect becomes less positive) at the higher-risk statuses. In other words, increased leisure boredom results in increased odds of smoking at lower risk levels (i.e., low and medium-low) but the impact is much less at higher risk levels (i.e., medium-high and high).

Discussion

The above results are interesting because we had been motivated by the hypothesis that we may find a causal effect among only those who were at highest risk. However, we found exactly the opposite. Leisure boredom had a significant effect on cigarette smoking initiation by the 1-year follow-up among those who were least at-risk (i.e., low and medium-low risk) of smoking initially. The predicted probability of smoking initiation in the high-risk status is the same (within rounding) regardless of the level of boredom (see Table 2). Thus, it appears that leisure boredom is not salient to those at high initial risk. This finding suggests that, in this case, it was helpful and informative to look at the ACE among different risk levels. In addition, this finding suggests that attempting to change leisure boredom through a universal intervention rather than targeting only those who are most at-risk would be important. Another more efficient option may be to have a leisure boredom intervention target only those who are at low risk and have another intervention target a different potential mediator for those who are most at-risk.

Limitations

A limitation of IPW is that, like all propensity score methods and all regression adjustments for confounding, it is assumed that there are no unmeasured confounders. Therefore, a randomized trial is the gold standard. However, it is not always possible. Although the no unmeasured confounding assumption cannot be tested in practice, sensitivity analysis methods have been developed for assessing the sensitivity of estimates to violations of the no unmeasured confounding assumption for categorical treatments (see e.g., Brumback et al. 2004). To our knowledge, sensitivity analysis for continuous treatments has not yet been developed and is an area for future research. Thus, caution should be exercised in the interpretation of the results from the empirical example because they are valid only if the no unmeasured confounders assumption holds.

A possible limitation of this analysis is that the students are nested within schools, which may violate the no-interference assumption. Methodological developments to address violation of this assumption in the potential outcomes framework is an ongoing area of research (e.g., Hong and Raudenbush 2005, 2006) and further developments are needed. For the purposes of this illustrative analysis, we assumed that estimates are robust to any violations of the no-interference assumption in order to simplify our introduction to these methods.

Alternative Approaches

There are other methods that could be used to construct the at-risk variable, such as a latent class model or classification and regression trees, but we used predicted probabilities from a logistic regression model to define the at-risk variable. An advantage of this is that we are able to summarize a large number of variables that predict risk status in a single number. Another advantage is that we do not need to be concerned with assigning individuals to a particular latent class; rather, the predicted probability from the at-risk model simply provides an indication of the individual’s initial risk of smoking. Nevertheless, construction of the propensity models and weights to estimate the causal effects can be used with other methods of constructing the at-risk variable. Likewise, our method of constructing the at-risk variable could be used in the case of a randomized trial, in which case it would not be necessary to adjust for potential confounding as long as the randomization did not fail.

To simplify interpretation, we stratified the moderator risk variable and treated it as a nominal variable. However, the risk status variable does not have to be stratified; because the hypothesized causal variable was continuous, it was easier to probe the interaction at one standard deviation above and below the mean level of boredom within strata of the at-risk variable. Although the estimates may be hand-calculated at one standard deviation above and below the mean, it is easier to construct new variables as described by Aiken and West (1991) and re-fit the models. It is not necessary to re-fit the propensity models or reconstruct the weights, as they are invariant to this transformation.

In summary, we have presented and illustrated the at-risk ACE, which provides an estimate of the causal effect of a variable, whether randomly assigned or not, on an outcome for different levels of initial risk for the outcome behavior. The initial risk status is a moderating variable and its inclusion allows the effect of a hypothesized cause on an outcome to vary across different groups of individuals. We believe that this estimate may be useful to prevention researchers because the effect of the hypothesized causal variable can differ across levels of initial risk. The model used for the denominator of the weights is not limited to the baseline confounders as illustrated here. Unlike standard propensity score methods such as matching (Rosenbaum and Rubin 1985) or subclassification (Rosenbaum and Rubin 1984), IPW is quite capable and, indeed, most typically used to handle time-varying treatments and confounders. An applied example of such an analysis in the prevention literature is given by Bray et al. (2006). Furthermore, MSMs are not limited to binary outcomes as illustrated here. For example, an MSM may be a linear regression in the case of continuous normally distributed outcomes or a survival analysis model in the case of censored outcomes (for an applied example, see Barber et al. 2004). It is also not necessary for the hypothesized causal variable to be binary; compared to other propensity score methods such as subclassification and matching, IPW can more easily handle continuous and ordinal treatment variables.

Appendix

R Code

The data set is read into R and is called “dat.” The variable c.bored2 is the mean-centered leisure boredom variable and smoke1, smoke2, and smoke3 are the lifetime smoking variables at baseline, 6 months, and 1 year, respectively.

#Model for creating at-risk variable
mod.risk <- glm(smoke1 ~ list of variables that predict initial risk, family=binomial,data=dat)
psmoke <- predict(mod.risk,newdata=dat, type=“response”)
z.breaks <- quantile(psmoke, probs=seq(from=0, to=1, by=.25), na.rm=TRUE)
dat$z.subclass <- cut(psmoke, z.breaks, include.lowest=T, labels=F)
dat$Zclass.1 <- 1*(dat$z.subclass==1)
dat$Zclass.2 <- 1*(dat$z.subclass==2)
dat$Zclass.3 <- 1*(dat$z.subclass==3)
dat$Zclass.4 <- 1*(dat$z.subclass==4)
#Limit data to those who had not yet started smoking at baseline or at 6 month
dat <- dat[dat$smoke1==0, ]
dat <- dat[dat$smoke2==0, ]
#Models for weights
num.mod.b <- lm(c.bored2 ~ z.subclass, data=dat)
den.mod.b <- lm(c.bored2 ~ list all confounders + z.subclass, data=dat)
sigma.n.b <- summary(num.mod.b)$sigma
sigma.d.b <- summary(den.mod.b)$sigma
#Obtain probabilities from normal p.d.f.
num.p.b <- dnorm(dat$c.bored2, mean=num.mod.b$fitted, sd=sigma.n.b)
den.p.b <- dnorm(dat$c.bored2, mean=den.mod.b$fitted, sd=sigma.d.b)
dat$wt.b <- num.p.b/den.p.b
#Fit the outcome model including the weights
design.ps.b <- svydesign(ids= ~1, weights= ~wt.b, data=dat)
msm.b <- svyglm(smoke3 ~ c.bored2 + as.factor(z.subclass) + c.bored2:as.factor(z.subclass), family = quasibinomial(), design=design.ps.b)
summary(msm.b)

SAS Code

The data set is read into SAS. It is originally called “leisure” and is in the library “atrisk.” The variable cbored2 is the mean-centered leisure boredom variable and smoke1, smoke2, and smoke3 are the lifetime smoking variables at baseline, 6 months, and 1 year, respectively.

*model for creating at-risk variable;
proc logistic data=atrisk.leisure descending;
 class list categorical predictors;
 model smoke1= name all predictors;
 output out=atrisk.smoke predicted=psmoke reschi=pearson resdev=deviance; run;
*”smoke” is a new dataset in the “atrisk” library that contains “psmoke”;
*create quartiles;
proc univariate data=atrisk.smoke;
 var psmoke;
 output out=quartile pctlpts=25 50 75 pctlpre=pct;
run;
data _null_;
set quartile;
call symput(‘q1’,pct25) ;
call symput(‘q2’,pct50) ;
call symput(‘q3’,pct75) ;
run;
data atrisk.smoke;
  set atrisk.smoke;
  strat1 = 0;
  strat2 = 0;
  strat3 = 0;
  strat4 = 0;
  if psmoke <= &q1 then strat1=1;
   else if psmoke <= &q2 then strat2=1;
   else if psmoke <= &q3 then strat3=1;
   else strat4=1;
run;
data atrisk.smoke;
 set atrisk.smoke;
 strat=.;
 if strat1=1 then strat=1;
 if strat2=1 then strat=2;
 if strat3=1 then strat=3;
 if strat4=1 then strat=4;
run;
*Limit data to those who had not yet started smoking;
data atrisk.smoke;
 set atrisk.smoke;
 if smoke1=1 then delete;
 if smoke2=1 then delete;
run;
*Models for weights;
proc reg data=atrisk.smoke;
  model cbored2 = strat;
  output out=atrisk.smoke student=rnum;
run;
quit;
proc reg data=atrisk.smoke;
  model cbored2 = strat confounders;
  output out=atrisk.smoke student=rden;
run;
quit;
*Obtain probabilities from normal p.d.f.;
data atrisk.smoke;
 set atrisk.smoke;
 pnum = exp(−.5*(rnum**2))/2.506;
 pden = exp(−.5*(rden**2))/2.506;
 ipw = pnum/pden;
run;
proc genmod data=atrisk.smoke;
 class id strat;
 model smoke3= strat cbored2 cbored2*strat /dist=bin link=logit;
 weight ipw;
 repeated subject=id /type=INDEP;
run;
quit;