Dynamics and Calcium Association to the N-Terminal Regulatory Domain of Human Cardiac Troponin C: A Multiscale Computational Study

Abstract

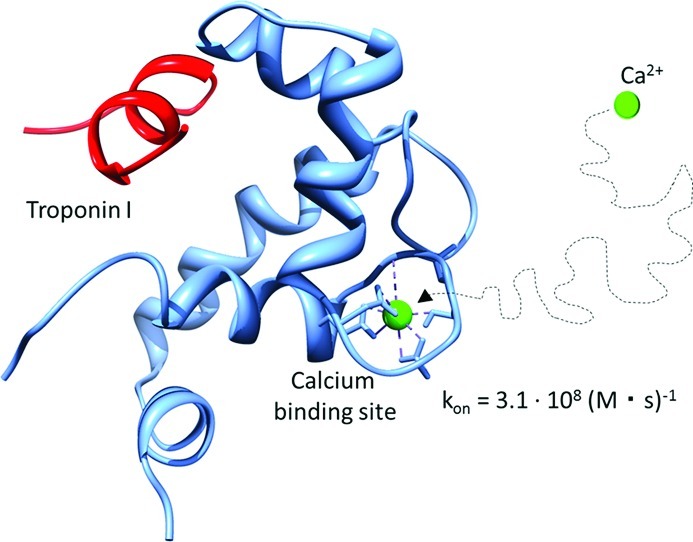
Troponin C (TnC) is an important regulatory molecule in cardiomyocytes. Calcium binding to site II in TnC initiates a series of molecular events that result in muscle contraction. The most direct change upon Ca²⁺ binding is an opening motion of the molecule that exposes a hydrophobic patch on the surface allowing for Troponin I to bind. Molecular dynamics simulations were used to elucidate the dynamics of this crucial protein in three different states: apo, Ca²⁺-bound, and Ca²⁺-TnI-bound. Dynamics between the states are compared, and the Ca²⁺-bound system is investigated for opening motions. On the basis of the simulations, NMR chemical shifts and order parameters are calculated and compared with experimental observables. Agreement indicates that the simulations sample the relevant dynamics of the system. Brownian dynamics simulations are used to investigate the calcium association of TnC. We find that calcium binding gives rise to correlative motions involving the EF hand and collective motions conducive of formation of the TnI-binding interface. We furthermore indicate the essential role of electrostatic steering in facilitating diffusion-limited binding of Ca²⁺.

Introduction

The contraction of cardiomyocytes has been studied extensively because it is crucial to proper heart function. Cross-bridges between actin and myosin lead to force generation and subsequently contraction. One important regulatory protein in the thin filament complex is troponin (Tn). Tn consists of three subunits: troponin C (TnC), troponin I (TnI), and troponin T (TnT).¹ Upon binding of the signaling ion, Ca²⁺, the N-terminal regulatory domain of TnC undergoes a structural reorganization that initiates myofilament contraction.² Calcium binding to TnC exposes a hydrophobic patch on TnC’s surface that promotes its association with the switch region of Troponin I (TnI). This in turn disturbs the interaction of the TnI inhibitory region with tropomyosin and actin, hence relieving TnI’s inhibition of contractile activity.^2,3 Therefore, Ca²⁺-binding to the 89 residue N-terminal regulatory domain of TnC presents a crucial step in a chain of events leading to a contractile response. Elucidating its structure and dynamics is central to studies of the role of calcium in myofilament contraction.

A plethora of structural studies have been carried out to elucidate the structure and function of the TnC regulatory domain of which nuclear magnetic resonance (NMR) has been particularly popular.⁴⁻⁷ Three states have been identified that are considered to be important intermediates in the myofilament contraction process: the free (apo) state, the Ca²⁺-bound state, and the Ca²⁺-TnI-switch-peptide-bound state. Additionally, the structures of the TnC regulatory domain in complex with small molecules⁸ and mutants of TnC have been elucidated. The regulatory domain, a highly α-helical molecule that constitutes the N-terminal half of the troponin C protein, consists of five α-helices (N, A–D). Helices A through D comprise two EF-hand helix–loop–helix motifs. The EF-hands, which are known to be metal-binding sites, are labeled sites I and II.⁹ In contrast with the C-terminal domain of TnC, which contains two high-affinity Ca²⁺-binding sites, the sites in the regulatory domain are of considerably lower affinity. Interestingly, in cardiac TnC, site I is completely defunct for calcium binding that is due to several amino acid substitutions with respect to site I in skeletal TnC.¹⁰ Site II, the low-affinity, Ca²⁺-specific Ca²⁺-binding site, is generally considered to be the only site directly involved in calcium regulation of cardiac muscle contraction.¹¹ Ca²⁺-binding to site II of cardiac TnC does not induce an opening transition akin to skeletal TnC¹² but leaves the structure more or less unperturbed in the closed conformation.^4,13 It is believed that the TnI switch peptide has to be present to stabilize the open conformation of the Ca²⁺-bound regulatory domain of cardiac TnC,^5,14 suggesting that the open conformation may only be a transient state that is sampled by TnC after Ca²⁺-binding.

In addition to the structural properties of TnC, its calcium exchange kinetics have been the focus of much experimental investigation.¹⁵ The calcium association rate to site II of isolated cardiac troponin C has been measured using stopped-flow techniques to be very high.¹⁶⁻¹⁸ Similarly, stopped-flow techniques^16,19and NMR spectroscopy²⁰ were able to determine Ca²⁺-dissociation rates from site II much faster than the time scale of muscle relaxation.

Although a wide variety of experimental techniques have shed light on the structure and function of TnC, atomistic level simulations of TnC structure and dynamics in various states of calcium and TnI switch peptide association are necessary for understanding the binding processes involved. As elucidation of the dynamics of the TnC regulatory domain in response to calcium binding is integral for estimating Ca²⁺ affinity, this work may also provide a platform for computationally calculating association and dissociation rates. Additionally, relaxed complex scheme type approaches²¹ could be used to generate actionable pharmaceutical leads by docking drug-like small molecules into structurally representative snapshots from molecular dynamics trajectories. In general, therapeutic strategies aim to improve calcium affinity in compromised tissue by changing the thermodynamics and kinetics of Ca²⁺ binding and TnI association. In this study, we use conventional and accelerated molecular dynamics (MD) to elucidate the dynamics of TnC with and without Ca²⁺ bound as well as with the TnI switch peptide bound. Comparison of molecular dynamics trajectories with experimentally obtained order parameters²² is used as an assessment of how well the conformational landscape conducive to Ca²⁺ binding is sampled. We examine TnC for its ability of binding Ca²⁺ and furthermore determine the molecular contributions to Ca²⁺ binding kinetics. The results of these studies can provide a framework for understanding impaired Ca²⁺ handling in TnC mutants and knowledge gained from this study will guide the improvement of inotropic pharmaceuticals that target TnC.

Material and Methods

System Preparation

Three different systems of human cardiac troponin C were prepared for simulations. The apo system was modeled based on model 13 from pdb entry 1SPY (89 residues⁴). The Ca²⁺-bound system was modeled based on model 14 from pdb entry 1AP4 (89 residues, Ca²⁺-ion⁴). The Ca²⁺-TnI-bound system was modeled based on model 18 from pdb entry 1MXL (106 residues, Ca²⁺-ion⁵). All systems were neutralized adding Na⁺ counterions (1AP4: 13 Na⁺, 1SPY: 15 Na⁺, 1MXL: 11 Na⁺) and solvated using a TIP3P water box. The fully solvated systems contained 24 316 (1AP4), 26 756 (1SPY), and 25 994 (1MXL) atoms, respectively. Minimization using SANDER²³ was performed in two stages: 1000 steps of minimization of solvent and ions (the protein is restrained using a force constant of 500 kcal/mol/Ų), followed by a 2500 step minimization of the entire system. A short initial 20 ps MD simulation with weak restraints (10 kcal/mol/Ų) on the protein residues was used to heat up the system to a temperature of 300 K.

Conventional MD and Accelerated MD Simulations

Both cMD and aMD simulations were performed under the NPT ensemble at 300 K for all three TnC systems using AMBER²³ and the ff99SB force field.²⁴ Periodic boundary conditions were used, along with a nonbonded interaction cutoff of 10 Å. Bonds involving hydrogen atoms were constrained using the SHAKE algorithm,²⁵ allowing for a time step of 2 fs. For each system, 100 ns MD trajectories were generated (for the Ca²⁺-bound system MD a trajectory of even 150 ns) as well as 50 ns aMD trajectories at four different acceleration levels. Acceleration parameters were determined based on average potential and dihedral energies of the equilibrated MD simulations. Dual boost aMD (both the dihedral energy and the total potential energy are boosted) was used. The acceleration level is defined in terms of E_b and α, where E_b is the threshold boost energy and α is a tuning parameter that determines the shape of the accelerated potential.²⁶ On the basis of a comparative analysis of previous successful aMD studies²⁷⁻²⁹ on a variety of systems of different sizes, the optimal boost energy for the torsional aMD is usually found to be the average dihedral angle energy plus 3.5 times the number of residues in the solute, and α should be ∼20% of E_b. Similarly the acceleration parameters for the acceleration of the total potential energy are dependent on the number of atoms in the entire simulation cell.^30,31 For the aMD simulations, a new in-house version of PMEaMD was used.

Clustering

Frames every 6 ps were extracted from the MD trajectories. The frames were aligned using all Cα atoms in the protein and subsequently clustered by rmsd using GROMOS++ conformational clustering.³² An rmsd cutoff of 1.6 Å (1AP4), 1.7 Å (1SPY) and 1.8 Å (1MXL) was chosen, respectively. These cutoffs resulted in 7 (1AP4), 9 (1SPY), and 8 (1MXL) clusters that represented at least 90% of the respective trajectories. The central members of each of these clusters were chosen to represent the protein conformations within the cluster and thereby the conformations sampled by the trajectory.

Principal Component Analysis

The principal component analysis (PCA) was performed using the bio3D package in R.³³ A blast profile of the 1AP4 sequence revealed 1056 hits. Out of the 35 most similar hits, 29 hits were chosen (excluding structures with mutations and the recently crystallized cadmium coordinating structure³⁴), and their experimentally determined structures were obtained from the protein data bank. The 29 structures underwent iterative rounds of structural superposition to determine the invariant core of the protein, a region that exhibits the least structural variance between the protein structures. This core consists of residues 17–28 and 72–79. Subsequently, the experimental structures were superimposed onto this core, and a PCA was employed.^35,36 In this process, a covariance matrix from the coordinates of the superimposed structures is diagonalized. The eigenvectors of this matrix represent the principal components of the system (parts of the structure within which there is the most variety among the set of superimposed experimental structures), whereas the eigenvalues are a measure of the variance within the distribution along the respective eigenvectors. All experimental structures have been projected into the space spanned by principal components one and two (along which there is the most variance among the structures). The principal component space generated based on the similar experimental structures served as basis for projection of the molecular dynamics trajectories. For the analysis of interhelical angles, interhelical angles were calculated using interhlx (K. Yap, University of Toronto).

Simulation of NMR Observables

On the basis of the MD trajectory of the Ca²⁺-bound system (1AP4), chemical shifts for the amide ¹H and the amide ¹⁵N were calculated using the SHIFTX software.³⁷ Protein structures were extracted from the trajectory every 20 ps. For each of these structures chemical shifts were calculated and averaged. Backbone N–H order parameters were calculated from the 100 ns molecular dynamics simulation of the apo system (1SPY) using the isotropic reorientational eigenmode dynamics (iRED) approach.³⁸ Order parameters were calculated by averaging 0.5 ns trajectory windows to ensure that the calculated S² parameters do not contain any motions whose time scale exceeds the overall tumbling correlation time of the protein.³⁹ The ptraj program was used to generate a list of eigenvalues and eigenvectors from all of the N–H backbone vectors with the ired method. On the basis of these lists, the order parameters are calculated using the mat2s2.py script.

Brownian Dynamics Simulations

BrownDye was used to estimate calcium association rates.⁴⁰ PQR files for representative protein structures determined by a cluster analysis were generated using pdb2pqr.⁴¹ The calcium pqr file was generated using a charge of +2 and an ionic radius of 1.14 Å. APBS⁴² was used to generate the electrostatic fields for the protein and the calcium ion in openDX format. Bd_top was used to generate all necessary input files for the BrownDye runs. A phantom atom of zero charge and negative radius (−1.14 Å) was introduced after the first execution of bd_top. The phantom atom was placed at the position of the calcium ion from the trajectory frame. It has no influence on the association rate constant calculation and serves solely to be able to define a reaction criterion that is spherically symmetric around the expected binding position of the calcium. The reaction criterion was chosen to be 1.2 Å within the calcium binding site. We performed 500 000 single trajectory simulations on 8 parallel processors using nam_simulation. The reaction rate constants were calculated using compute_rate_constant from the BrownDye package. A weighted average of the rate constants of each of the representative cluster centers yielded an estimate of the overall rate constant for the system.

Results & Discussion

Sampling by Conventional MD versus Accelerated MD

PCA characterizes collective, high-amplitude structural variations based on a set of homologous protein structures. The predominant modes provide a basis for analyzing large-scale conformational changes anticipated in MD simulations. In this study, NMR structures of apo-TnC, Ca²⁺-bound TnC, Ca²⁺/TnI-bound TnC, and TnC in complex with compounds such as bepridil, W7, and dfbp were used as inputs for PCA. The first two principal components, PC1 and PC2, are illustrated in Figure 1and account for 50.9 and 13.5%, respectively, of the variance associated with known TnC structures. As the two components together account for 64.4% of the variance, it was considered to be appropriate to analyze the simulations just in terms of these components. PC3 accounts for another 10.4% of the variance but was not used for analysis because of its relatively low contribution. The quadrants along PC1 and PC2 describe apo and Ca²⁺-bound TnC structures (lower right, e.g., 1SPY, 1AP4) and Ca²⁺-TnI-bound TnC structures (left side, e.g., 1MXL, 2L1R).

Figure 1.

PCA plot comparing cMD and aMD trajectory sampling for the Ca²⁺-bound system. The principal component space generated by known structures of TnC is shown along with molecular dynamics trajectories that are projected into the first versus second principal component space of known TnC structures. (A) Projections of known pdb structures are shown as filled circles. The NMR structures of 1AP4, 1SPY, and 1MXL are shown as filled green, red, and blue circles, respectively. (B) Projection of the 1AP4 cMD trajectory (full blue circles) into the PC space is shown in density coloring where darker shades of blue indicate the more heavily sampled parts of the trajectory. (C) Projection of the 1AP4 aMD trajectory (full blue circles) into the PC space is shown in density coloring. (D) Projections of the 1AP4 cMD trajectory (full red circles) and the 1AP4 aMD trajectory (full blue circles) into the PC space are shown in density coloring, where darker shades of red and blue indicate the more heavily sampled parts of the trajectories. cMD and aMD trajectories overlap with extended sampling for the accelerated method. Complete overlap of most heavily sampled regions for the aMD trajectory with the cMD trajectory suggests that cMD samples most of the statistically relevant conformations for this system.

Figure 2 summarizes the motions corresponding to the first two principal components. PC1 corresponds to a concerted motion of helices B and C opening up the structure and changing the A/B interhelical angle. It appears that the motion connected to PC1 is primarily connected to an opening motion that presents the hydrophobic patch comprising the TnC/TnI interface. (See for instance ref (8).) The motion associated with PC2 whose amplitude is considerably smaller than that of PC1 pulls away helices B and C from helix A. Together with the motion represented by PC1 this motion seems to expose the hydrophobic patch even further.

Figure 2.

Motions associated with first two principal components. A principal component analysis of the conventional MD trajectory of the calcium bound TnC regulatory domain (1AP4) was performed. The range of motions associated with PC1 (A) and PC2 (B) is shown as the overlay of two structures. Movement of helix A is not part of the first two principal components. The biggest difference between PC1 and PC2 is apparent in the movement of helix B. In the motion associated with PC1, helix B slides with respect to helix A, whereas it is tilted toward helix A in the motion associated with PC2.

PCA gives information about both the main internal protein motions during molecular dynamics simulations as well as about the overall structural space sampled by the simulations. For all three troponin C systems (apo, Ca²⁺-bound, and Ca²⁺-TnI-bound), at least 100 ns of conventional MD (cMD) as well as 50 ns of accelerated MD (aMD) were performed. Prior studies^28,43 have demonstrated that predominant PCA modes are related to low-frequency collective motions; therefore, we project these data along the PC modes 1 and 2. Figure 1 shows the projection of the 1AP4 cMD and aMD trajectories into PC space as well as an overlay of the two. cMD and aMD share the same peak density location at about (25 Å, −5 Å). This minimum coincides with projection of the 1AP4 and 1SPY crystal structures, suggesting a significant energetic barrier to sampling the TnI-bound state. The aMD trajectory uncovers several regions of intermediate density, most notably a possible secondary minimum around (25 Å, 0 Å), thus indicating its efficacy in traversing moderate conformational barriers. In the aMD simulation, we also note a greater sampling of the PC2 conformational motion toward the Ca²⁺-TnI-bound state at about (−10 Å, 5 Å). This suggests that the Ca²⁺-bound form approaches TnI-compatible states in the absence of TnI, although there is a risk that the modified potential inherent to aMD samples improbable reaction pathways. Whereas cMD samples a lesser extent compared with aMD, the vast majority of the sampled population is located within the region of PC space sampled by cMD centered at (25 Å, −5 Å). These conformations thus dominate the thermodynamics of the system.

Additionally the root-mean-square fluctuations (RMSFs) were compared between the cMD and aMD simulations. The general trend for both cases is identical in that the most flexible residues are in the N-terminal and C-terminal regions of the protein (residues 1–4, 87–89) corresponding to flexible loops at the termini. The most flexible region within the protein is the dysfunctional Ca²⁺ binding site I (residues 28–37). In the cMD simulations, RMSF values for residues 50–70 (including the Ca²⁺ binding site II) are slightly more flexible (RMSF ≈ 1.5 Å) than the background at 1 Å. While leaving the general trend unchanged, the aMD simulations increase the background RMSF level slightly (to ∼1.5 Å) and show slightly larger RMSF values for residues 50–70, which also include the Ca²⁺ binding site II. Later, we demonstrate that cMD-sampled states capture the dynamics observed in NMR chemical shift and order parameters. Therefore, we expect that cMD is sufficient for generating thermodynamically relevant information, whereas aMD may be required for assessing transient states leading to binding of TnI or other small molecule ligands.

Accelerated MD Reveals Opening Transition in Ca²⁺-Bound TnC Not Present in the apo Form

PCA can be used to compare the different simulated systems (apo, Ca²⁺-bound, and Ca²⁺-TnI-bound) in terms of collective motions bridging the different states. To compare the dynamics of the three systems under investigation, we plotted the projection of the cMD and aMD trajectories into the principal component space. In the cMD simulations, the structures and dynamics of the apo (1SPY) and Ca²⁺-bound (1AP4) systems are very similar, as seen by their virtually overlapping projections into PC space (Figure 3). The aMD simulations, however, reveal subtle yet significant differences in the dynamics of the apo and Ca²⁺-bound forms. The area sampled in PC space is larger for the Ca²⁺-bound system. The simulations of the Ca²⁺-TnI-bound system (1MXL) predominantly sample a different section of the principal component space generated based on known structures of TnC. These motions are indicative of the open conformation of TnC², facilitated by the binding of TnI. (See Figure 3.) In particular, residues 36–50 are nearly rigid in the TnI-free simulation (RMSF of ∼1 Å) but become highly mobile in the presence of TnI with RMSF values ranging between 1.5 and 2.5 Å. This suggests that the TnI-bound structure exists in an energy well that is distinct from the apo and Ca²⁺-bound forms of TnC. Given that these dynamics were not even observed with aMD sampling, we speculate that there is a high energy barrier between the apo and Ca²⁺-bound states on the one side and TnI-bound states on the other.

Figure 3.

PCA plot comparing conformational dynamics sampling between the apo, Ca²⁺-bound and Ca²⁺-TnI-bound system. The principal component space generated by known structures of TnC is shown along with molecular dynamics trajectories that are projected into the first versus second principal component space of known TnC structures. (A) Projections of known pdb structures are shown as filled circles. The NMR structures of 1AP4, 1SPY, and 1MXL are shown as filled green, red, and blue circles, respectively. (B) Projections of the Ca²⁺-bound TnC for the 1AP4 cMD trajectory (full blue circles), the 1SPY cMD trajectory (full red circles), and the 1MXL cMD trajectory (full green circles) into the PC space are shown in density coloring, where darker shades of blue, red, and green indicate the more heavily sampled parts of the trajectories. (C) Projections of the Ca²⁺-bound TnC for the 1AP4 aMD trajectory (full blue circles), the 1SPY aMD trajectory (full red circles), and the 1MXL aMD trajectory (full green circles) into the PC space are shown in density coloring, where darker shades of blue, red, and green indicate the more heavily sampled parts of the trajectories. For the conventional molecular dynamics simulations, the principal component space sampled by the apo and Ca²⁺-bound systems is almost identical indicating similar dynamics. In the aMD simulations, however, occasional excursions of the Ca²⁺-bound system into Ca²⁺-TnI-bound-like states are observed. The Ca²⁺-TnI-bound system, however, samples a different, hardly overlapping region of the PC space, suggesting a change in dynamics upon TnI binding.

Additionally, to investigate more closely the opening transition believed to be crucial to TnI binding, the interhelical angle analysis was performed. Plotting the A/B angle over the course of the simulations has the potential of identifying transitions between open and closed states as well as possibly making a statement about the time scale of helical motions connecting the states. The concerted motion of helices B and C away from helix A presents the most notable structural change involved in exposing the hydrophobic spot on the TnC surface that facilitates TnI binding. Therefore, the interhelical A/B angle has been reported as a good indicator of the degree of opening in the TnC protein,⁸ with angles around 135° corresponding to a closed conformation and angles around 90–100° characterizing the open conformation. (See panels A and B of Figure 4.) This is corroborated by comparing the interhelical angle measurements over the course of the cMD simulations (Figure 5). The interhelical A/B angles fluctuate around an average of ∼135° for both the apo and Ca²⁺-bound system and range from ∼115 to 150°. No opening transitions are seen. The aMD simulations, however, reveal subtle yet significant differences in the dynamics of the apo and Ca²⁺-bound forms. The area sampled in PC space is larger for the Ca²⁺-bound system, corresponding to the apo and the Ca²⁺-bound structures sampling a wider range of angles. The most open conformation seen for the apo system still has an angle of ∼105°, which is inconsistent with a full opening transition, yet there are several structures in the Ca²⁺-bound simulation where the interhelical A/B angle is very close to the ∼90° of the open conformation. (See Figure 4C.) This, in agreement with ref (2), suggests that binding of calcium subtly changes the dynamics of the system, allowing for opening transitions that are not seen in the apo form. It appears that the open conformation is short-lived. Despite the fact that due to the acceleration we may underestimate the duration the system spends in the open state, this corroborates the notion of the open state being a nonstable transient one that has to be stabilized by the presence of the TnI switch peptide.^5,14 These results, to the best of our knowledge, are the first time that an opening transition for cardiac TnC has been observed in a molecular dynamics simulation. It is worth noting that the opening transition is also observed in the PCA analysis. As previously noted, PC 1 corresponds to the motion associated with opening. In the projection of the aMD trajectory into PC space (Figure 1C), there are multiple structures observed around (−5 Å, −25 Å), which come very close to the open conformation (−10 Å, 5 Å) along PC1, indicating a decreased A/B interhelical angle. These structures are not present in the projection of the cMD trajectory (Figure 1B).

Figure 4.

Structures and helix nomenclature of cardiac TnC. (A) NMR structure of Ca²⁺-bound TnC (1AP4), (B) NMR structure of Ca²⁺-TnI-bound TnC (1MXL), and (C) structure of frame 9840 of the 1AP4 aMD simulation are shown. For the purpose of clarity, the TnI switch peptide has been removed from panel B. For all panels, the helix assignment in the regulatory domain of cardiac TnC is shown. The most N-terminal helix is denoted by N, followed by helices A through D. The interhelical angle between helices A and B is used to measure the degree of openness of the domain. (A) Ca²⁺-bound NMR structure is in the closed state with an A/B interhelical angle of around 135°. (B) Ca²⁺-TnI-bound NMR structure is in the open state with an A/B interhelical angle of around 90°. (C) Frame 9840 corresponds to the most open conformation sampled during the 1AP4 aMD simulation. The molecule adopts the open conformation with an A/B interhelical angle of 93°.

Figure 5.

Evolution of A/B interhelical angle over the course of the simulations. The interhelical angle between helices A and B has been calculated for every frame of the TnC simulations. Results for the apo cMD simulation (A), the apo aMD simulation (B), the Ca²⁺-bound cMD simulation (C), and the Ca²⁺-bound aMD simulation (D) are shown. aMD simulations sample a considerably wider range of interhelical angles. The most open conformation (A/B interhelical angle 93°) observed in the simulations is labeled with a black circle in panel D.

Furthermore, a cross-correlation analysis was performed to elucidate intramolecular fluctuations unique to each state. The cross-correlation analysis of the trajectories (Figure 6) revealed positive correlated motion in the strands of the central β-sheet (C35-S37, T71-D73) linking both EF-hands in the apo simulations and the cMD Ca²⁺-bound simulation, as previously reported in ref (44). This positive correlation is reversed into a negative correlation in the Ca²⁺-bound aMD simulation (Figure 6D). Whereas this was not observed in ref (44), we believe that the relatively short simulation time (6 ns) would not capture longer-time scale motions that could contribute to anticorrelated motions. Therefore, we speculate that the disruption of the correlated motion in the β-sheet corresponds to helix B pivoting away from helix A as part of an opening event. Another region of correlated motion that is consistently present in most simulations is the interface between helices N and D. This suggests the presence of strong hydrophobic contacts between the helices possibly stabilizing the fold. On the basis of the simulation results, it is hard to speculate on the time scale of the opening/closing transition, but it is very likely to be well beyond the 100 ns mark. Future work will focus on running longer cMD simulations that reveal several opening/closing transitions and allow for an estimation of the [open]/[closed] equilibrium and a free energy difference of the transition.

Figure 6.

C_α-residue cross correlation plots for the (A) apo cMD, (B) apo aMD, (C) Ca²⁺-bound cMD, and (D) Ca²⁺-bound aMD simulations. Green regions mark areas of positive cross correlation while red regions specify areas of negative cross correlation.

Chemical Shifts and Order Parameters Calculated from Trajectories Are in Good Agreement with Experiment

Chemical shifts derived from NMR data describe the local electronic environment about labeled nuclei and serve as a structure determination tool.⁴⁵ In this experiment, we predicted chemical shifts from the MD trajectories to demonstrate that states analogous to those observed in solution NMR are sampled. To this end, amide ¹H and ¹⁵N chemical shifts were calculated from the cMD trajectory for the Ca²⁺-bound TnC system, which are compared with chemical shifts obtained by NMR spectroscopy²⁰ in Figure 7. The calculated shifts show surprisingly good agreement with experimental values, as the determined average root-mean-square deviations between the calculated and experimental chemical shifts are 0.4 ppm for the ¹H shifts and 2.9 ppm for the ¹⁵N shifts, compared with the precision of SHIFTX of 0.49 ppm for amide ¹H chemical shifts and 2.43 ppm for amide ¹⁵N chemical shifts.³⁷ Chemical shifts were calculated from the aMD trajectory as well and are only marginally better with average root-mean-square deviations between the calculated aMD and experimental chemical shifts of 0.5 ppm for the ¹H shifts and 2.6 ppm for the ¹⁵N shifts. It is not surprising that no substantial differences between cMD and aMD predicted chemical shifts is observed as the simulations identify the same thermodynamically dominant regions on the potential energy surface as demonstrated by PCA. Additionally, the majority of the slow time-scale dynamics observed in the simulations are concerned with tertiary structure and not changes in the secondary structure. Therefore, they may not be picked up by SHIFTX, an algorithm predominantly based on local sequence and local secondary structure.

Figure 7.

Comparison of experimental and calculated chemical shifts. Residue-by-residue comparison of experimentally determined chemical shifts (blue) and chemical shifts calculated from the cMD trajectory of the Ca²⁺-bound TnC system (red with error bars). Panel A shows the amide ¹H chemical shifts alongside a ribbon representation of TnC, where the residues for which the predicted ¹H chemical shifts deviate more than two standard deviations from the experimental value are labeled in red. Panel B shows the amide ¹⁵N chemical shifts alongside a ribbon representation of TnC where the residues for which the predicted ¹⁵N chemical shifts deviate more than two standard deviations from the experimental value are labeled in red.

Figure 7 also shows the residues in the protein for which the chemical shifts deviate the most from experiment. Chemical shifts of two of the residues whose ¹H and ¹⁵N chemical shifts deviate from experimental values (72 and 73) have been previously reported to be greatly impacted by calcium binding⁴⁶ both experimentally and using quantum mechanical calculations. In general, whereas these sites are distributed throughout the entire molecule, there is an increased occurrence of incorrectly predicted shifts in the calcium binding site II and neighboring regions. The deviation of the predicted chemical shifts and experimental values can be attributed to a number of possible causes. It has been suggested⁴⁵ that MD-generated structures typically give inferior shifts compared with those generated from a molecular mechanics conformational search, even when using quantum mechanical estimates of the nuclear magnetic shieldings. Therefore, it is possible that these simulations still undersample the conformational states contributing to the NMR observable. More specifically, the deviations close to the calcium binding site could be attributed to SHIFTX not being well-parametrized for the prediction of metal binding sites in general.³⁷ Another possible source of error is the use of nonpolarizable force fields in the simulations. For highly charged interactions like the ones between calcium and the negatively charged EF-hand residues, ignoring polarization effects might introduce additional error.⁴⁷ Use of polarizable force fields in future calculations may recover some of the error.

Backbone order parameters were calculated from the cMD trajectory for the apo TnC system and compared with the experimentally determined order parameters for the apo form of the regulatory domain of human cardiac troponin C.²² Figure 8 shows the overlay of the calculated and experimental order parameters. The regions of greatest flexibility (lowest order parameters) are the two calcium binding loops, calcium binding sites I (inactive) and II (low affinity binding site), as well as the N- and C-terminal residues. The overall agreement of the calculated and experimental data is good with an average deviation of less than 0.03. In agreement with previous experimental studies,^22,48 the simulations identify positions 2–6 (corresponding to residues 66–70) in both sites I and II as the most flexible residues of the protein. This is not surprising as these highly charged residues are very labile in the absence of Ca²⁺. Interestingly the most significant deviations between prediction and experiment are residues 42–49 (corresponding to helix B), with a general trend of overestimating order parameters (i.e., underestimating the dynamics). Future work will focus on comparing order parameters calculated from longer simulations to experimental values. Little overall changes can be observed when comparing the calculated order parameters for the Ca²⁺-bound simulation with the apo simulation (Figure8B). In agreement with observations made in ref (48), the order parameters in the calcium binding site II decrease, consistent with decreased flexibility due to calcium binding.

Figure 8.

Comparison of experimental and calculated order parameters. (A) Backbone N–H order parameters were calculated for the apo TnC system and are compared with the experimentally determined NMR order parameters. Calculated order parameters for all residues are shown in red, whereas the experimentally determined parameters at 25 °C are shown in green. The simulation was performed at 300 K (26.85 °C). Agreement of calculated and experimental order parameters is particularly striking in the N-terminal part of the protein including the inactive (around residue 30) calcium binding site. (B) Comparison of calculated order parameters for the apo (blue) and Ca²⁺-bound (purple) TnC system. Order parameters generally agree between the systems with the exception of the calcium binding site II.

The agreement of calculated and experimentally observed chemical shifts and order parameters indicates that the molecular dynamics simulations did cover the relevant dynamics of the isolated protein domain. Therefore, these results provide an important measure of confidence that the dynamics seen in the calculations capture the predominant dynamics of the protein and that other quantities calculated based on the trajectories most likely represent thermodynamically relevant measures as well.

Investigating Calcium Association with Brownian Dynamics Simulations

Brownian dynamics simulations have been used to estimate the association rate constant for calcium binding to troponin C. For this, the cMD trajectory for the Ca²⁺-bound TnC system was clustered by rmsd, and seven representative structures (cluster centers) that represented more than 90% of the structures seen in the trajectory were extracted. We performed 500 000 single trajectory Brownian dynamics simulations for each of these representative structures. The average calcium association rate constant was determined to be with 3.1 × 10⁸ 1/(M·s). Diffusion-limited association rates have been reported in the literature, for instance, (2 to 4) × 10⁸ 1/(M·s)¹⁷, 4 × 10⁷ 1/(M·s)¹⁸, and 1.4 × 10⁸ 1/(M·s)¹⁶. The calculations based on Brownian dynamics and the cMD trajectories reproduce the experimentally observed rates well. To investigate whether there was any variation of the association rate over the course of the simulation, calcium association rates were calculated for a structure extracted every 1.5 ns from the trajectory. No appreciable variation in association rate between different structural states is observed, leading us to speculate that the binding site always assumes on “open” conformation. Therefore, gating has no effect on calcium association. Furthermore, in agreement with trends reported by ref (18), we observe that ln(k_on) decays linearly with the root of ionic strength (sqrt(I)) (Figure 9). This underscores that electrostatics play a crucial role in the association of calcium. These results underscore that Brownian Dynamics simulations are an important and viable tool to investigate the calcium association in troponin C.

Figure 9.

Dependence of ionic strength on calcium association rate. The square root of ionic strength is plotted versus the natural logarithm of calcium association rate. A linear dependence can be observed.

Conclusions

Here we presented medium-length molecular dynamics simulations on three different states of the regulatory domain of troponin C. Motions that correspond to the greatest variation within known TnC structures were elucidated. For the first time, the opening motion of Ca²⁺-bound TnC has been observed and could be attributed to a concerted tilting motion of helices B and C away from helix A, which is implicated in TnI binding and activation of myofilament contraction. The focus of future microsecond time scale cMD simulations will be elucidation of the time scale (frequency and duration) of the opening event. The results concerning the opening motion represent an important first step in understanding the function of the entire troponin molecule as they lay the foundation of understanding the molecular events that govern association of TnC with TnI, a crucial step in muscle contraction. Agreement of simulated NMR observables with experimental values implies that the simulations sample thermodynamically relevant conformations. Calcium association studies using Brownian dynamics simulations yield diffusion-limited association rates and correct trends with varying ionic strength of the solution, suggesting an important role of electrostatics in rapid Ca²⁺-binding. However, desolvation effects cannot be neglected when attempting to predict quantitatively the rates. Future work will focus on using polarizable force-field simulations on TnC. Besides yielding important information concerning Ca²⁺-binding and opening properties, our studies will be the basis of relaxed complex scheme computer-aided drug design studies involving TnC. The accelerated MD studies presented here did identify intermediate structures not sampled by conventional MD simulations and thus will be able to provide an extended set of possible receptor conformations for drug design studies. Additionally, the results presented here may eventually have the potential to inform mesoscale models of myocyte contractility.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States