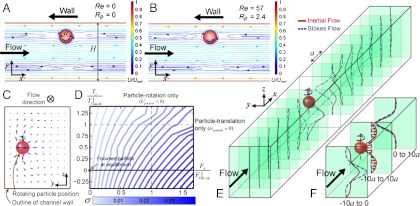
Fig. 1.
Particle-induced convection due to a combination of confinement and inertia. (A, B) Reversing streamlines in the particle frame of reference for Stokes and inertial flow, respectively. The reversing streamlines are present in confined flow, even when inertia is neglected. (C) Particle-induced convection, the net secondary flow created by the inertial effects of the fluid around a rotating particle, is observed by integrating the net lateral velocity (y and z components) along the x axis for local y-z positions in the channel cross-section. (D) Scaling of net lateral fluid velocity (σ) with drag (Fx) and torque (Tz) imposed on the particle. Drag and torque are normalized by the drag on a stationary particle (Fx|V=0) and torque on a nonrotating particle (Tz|ω=0). Numerical simulations suggest that increasing drag (i.e., a particle lagging the downstream flow) and decreasing torque (i.e., a faster rotating particle) lead to an increase in velocity of the net secondary flow. (E) Transport of the fluid across the channel is shown at different intervals along the channel, for Stokes and inertial flows. For Stokes flow (dashed blue lines) symmetric transport upstream and downstream is observed. For the inertial flow (solid red line) the transverse transport is asymmetric. Upstream of the particle, the transverse shift of the fluid is delayed compared to Stokes flow, while downstream the flow diverted around the particle again lags the Stokes flow situation. (F) Net transport upstream, downstream, and over the total length of the channel is shown. Overall transport downstream is quite similar between Stokes and inertial flow. However, upstream transport results in the main overall difference. While there is no net transfer of fluid in Stokes flow, because the fluid is symmetrically diverted around the particle, significant transfer is observed in inertial flow.