Estimation of Blood Flow Rates in Large Microvascular Networks

Abstract

Objective

Recent methods for imaging microvascular structures provide geometrical data on networks containing thousands of segments. Prediction of functional properties, such as solute transport, requires information on blood flow rates also, but experimental measurement of many individual flows is difficult. Here, a method is presented for estimating flow rates in a microvascular network based on incomplete information on the flows in the boundary segments that feed and drain the network.

Methods

With incomplete boundary data, the equations governing blood flow form an underdetermined linear system. An algorithm was developed that uses independent information about the distribution of wall shear stresses and pressures in microvessels to resolve this indeterminacy, by minimizing the deviation of pressures and wall shear stresses from target values.

Results

The algorithm was tested using previously obtained experimental flow data from four microvascular networks in the rat mesentery. With two or three prescribed boundary conditions, predicted flows showed relatively small errors in most segments and fewer than 10% incorrect flow directions on average.

Conclusions

The proposed method can be used to estimate flow rates in microvascular networks, based on incomplete boundary data and provides a basis for deducing functional properties of microvessel networks.

INTRODUCTION

Methods for structural imaging of microvascular networks have developed rapidly in recent years and can provide detailed information on three-dimensional networks containing thousands of segments. Available methods include confocal imaging [2], reconstruction from serial sections [4, 6, 11, 25] and micro-CT imaging [1, 3, 5]. These methods can be used to visualize and quantify the complete vascular structure within tissue volumes of several cubic millimeters. When combined with appropriate automated image processing algorithms [8, 13], such data can be used to derive quantitative structural information in terms of the positions, lengths, diameters and connectivity of the vessel segments forming the network.

The distribution of blood flow rates in microvascular networks fundamentally influences perfusion, solute transport, flow regulation, and growth and adaptation in the vascular system. However, available methods for direct observation of blood flow within individual vessels, such as intravital microscopy or endocardial probes, are largely limited to sheet-like or surface vascular networks. Approaches that can be used to measure microvascular flow in thicker tissues, such as laser-Doppler flowmetry, Doppler optical coherence tomography or magnetic resonance perfusion imaging, do not resolve individual microvessels, and yield spatially averaged measurements. The ability to analyze and predict the functional properties of observed microvascular network structures is thus hindered by the lack of correspondingly detailed flow information.

Previous studies have provided a basis for predicting the distribution of blood flow in microvascular networks [9, 20], taking into account effects resulting from the particulate nature of blood. In these studies, the apparent viscosity of blood has typically been characterized as a function of microvessel diameter and hematocrit using an empirical model [17, 23]. At diverging bifurcations, red blood cells are generally distributed such that daughter vessels at diverging vessel bifurcations receive different hematocrits. Typically, the daughter vessel with the higher flow rate has a larger discharge hematocrit. This unequal distribution of hematocrit has been described by empirical models that depend on the diameters and flow rates in the parent and daughter vessels and the hematocrit in the parent vessel [16, 17]. These relationships are key components of models to predict the distribution of flows and hematocrits in a network, given information on the diameters, lengths and topological arrangement of all segments [10, 22].

However, simulations of blood flow in a network also require boundary conditions, in the form of flow or pressure values at all boundary nodes of the network and hematocrit values at all nodes receiving inflows to the network. The large network structures that have been experimentally observed typically have many boundary nodes. This is because the boundaries of the region of observation do not coincide with tissue boundaries, meaning that they intersect with a large number of vessel segments. The flows in the major feeding and draining vessels can potentially be measured directly or deduced from measured or typical values of tissue perfusion, but the flows in the numerous smaller microvessels forming the network boundary are generally unknown, and must be estimated by some means. One approach is to assign pressure or flow values to boundary vessels, based on typical values for vessels with similar diameters or types [12, 14]. This approach inevitably involves some arbitrary assumptions, and may result in unrealistic uniformity in parameter values, for instance if all boundary capillaries are assigned equivalent flows or pressures. Therefore, an alternative approach is proposed here. This approach involves minimizing the sum, over all segments in the network, of the squared deviations of wall shear stresses and pressures from target values derived from independent information about typical network hemodynamic properties. The goal of the present study is to develop and test a new mathematical and computational algorithm based on this approach.

METHODS

Network hemodynamics

The flow rate Q_j in segment j of the network is assumed to be governed by Poiseuille’s law with an effective viscosity μ_j. For each segment, a positive flow direction is defined, from start node to end node. The relationship between the nodal pressures p_k and the segment flows can be expressed in matrix form as

$$Q_j=\sum _{k\in N}{M}_{jk}{p}_k,$$ (1)

where N is the set of all nodes (junctions) in the network and

$$M_{jk}=\{\begin{array}{cc}+\pi r_j^4/(8{\mu }_j{\ell }_j),& \text{if}k\text{is}\text{the}\text{start}\text{node}\text{of}\text{segment}j\\ -\pi r_j^4/(8{\mu }_j{\ell }_j),& \text{if}k\text{is}\text{the}\text{end}\text{node}\text{of}\text{segment}j\\ 0,& \text{otherwise}\end{array}$$ (2)

where r_j, ℓ_j and μ_j denote the radius, length and effective viscosity of segment j. By conservation of mass, the sum of the flows at each interior node is zero. This condition can be combined with the conditions on the boundary nodes to give

$$\sum _{j\in S}{L}_{ij}{Q}_j+Q_{0i}=0\mathit{for}i\in N$$ (3)

where S denotes all segments in the network, and

$$L_{ij}=\{\begin{array}{cc}-1,& \text{if}i\text{is}\text{the}\text{start}\text{node}\text{of}\text{segment}j\\ +1,& \text{if}i\text{is}\text{the}\text{end}\text{node}\text{of}\text{segment}j\\ 0,& \text{otherwise}\end{array}$$ (4)

If node i is a boundary node, then Q_0i is the inflow (or outflow, if negative). At interior nodes, Q_0i = 0. Combining (1) and (3) yields

$$\sum _{k\in N}{K}_{ik}{p}_k=-Q_{0i}\mathit{for}i\in N$$ (5)

where

$$K_{ik}=\sum _{j\in S}{L}_{ij}{M}_{jk}.$$ (6)

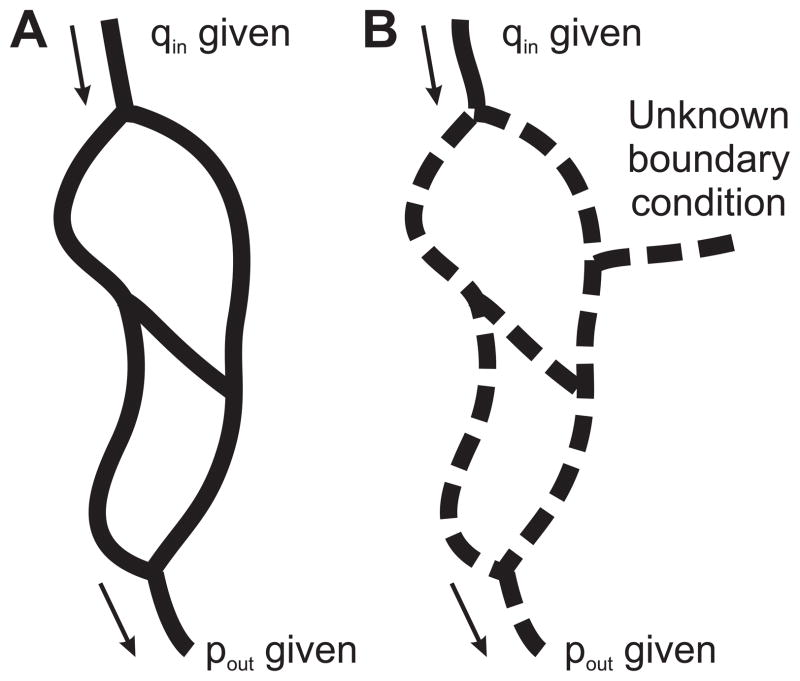
A pressure boundary condition can be imposed at node i by replacing the i-th row of the matrix K with a single diagonal entry of 1 and replacing −Q_0i by the prescribed pressure. If the pressure or flow is known at every boundary node (Figure 1A), then the system (5) is fully determined and can be solved by standard methods [10, 22].

Figure 1.

A. If boundary conditions (pressure or flow, including at least one pressure boundary conditions) are specified at all boundary nodes of a network, and the flow resistances of all segments are known, then the flow rates in all segments of the network are fully determined (solid lines). B. With incomplete boundary data, the equations governing flow in the network lead to an underdetermined linear system, and flows in some segments remain as unknowns (dashed lines).

The effective viscosity μ_j in segment j is determined as a function of the radius r_j and the hematocrit H_Dj of each segment, using an empirical in-vivo viscosity relationship [23]. The hematocrits can be computed from the flow rates Q_j, using empirical relationships for hematocrit partition at diverging bifurcations [16, 17]. In order to satisfy these relationships, an iterative procedure is required to solve for the flows, hematocrits, and effective viscosities in each vessel. Specifically, the flow in each vessel is calculated with initial values for discharge hematocrit. These flow values are then used to update H_Dj in each vessel. Effective viscosity is then recalculated using the new hematocrits. These steps are repeated until convergence is reached for Q_j, H_Dj, and μ_j in each vessel.

Estimation of flows with incomplete boundary conditions

We now address cases for which boundary conditions, in the form of specified flow or pressure at each boundary node, are known only at a subset of the boundary nodes (Figure 1B). If the boundary conditions are not all known, the system (5) becomes

$$\sum _{k\in N}{K}_{ik}{p}_k=-Q_{0i},i\in I\cup B$$ (7)

where I is the set of interior nodes and B is the set of boundary nodes with known boundary conditions. This system is underdetermined and has multiple solutions. In order to obtain a unique solution, additional assumptions are required. In the present model, it is assumed that information is available about the typical distributions of pressure and wall shear stress in the network, such that a target pressure and wall shear stress can be defined for each segment. The specification of these target values is discussed further below. Using these distributions, a solution is sought that minimizes the total squared deviation D from the target values of pressures and wall shear stresses:

$$D=\frac{1}{2}{k}_p\sum _{k\in N}{w}_k{(p_k-p_{0k})}^2+\frac{1}{2}{k}_{\tau }\sum _{j\in S}{\ell }_j{({\tau }_j-{\tau }_{0j})}^2.$$ (8)

Here, τ_j is the wall shear stress in segment j, τ_0j is the corresponding target shear stress, p_0k is the target pressure at node k, k_p and k_τ are weighting factors associated with the pressure and shear deviations from the target values, and w_k is the vessel length associated with node k, defined as

$$w_k=\frac{1}{2}\sum {\ell }_j$$

where the sum is over the segments j connected to node k. This constrained optimization problem can be formulated in terms of a Lagrangian objective function

$$L=\frac{1}{2}{k}_p\sum _{k\in N}{w}_k{(p_k-p_{0k})}^2+\frac{1}{2}{k}_{\tau }\sum _{j\in S}{\ell }_j{({\tau }_j-{\tau }_{0j})}^2+\sum _{i\in I\cup B}{\lambda }_i\left(\sum _{k\in N}{K}_{ik}{p}_k+Q_{0,i}\right)$$ (9)

where λ_i are Lagrange multipliers. At the solution, L is stationary with respect to the unknowns p_i and λ_i. In each segment, the shear stress is proportional to the flow rate:

$${\tau }_j=c_j{Q}_j=c_j\sum _{k\in N}{M}_{jk}{p}_k,$$ (10)

where c_j = 4μ/(πr_j³) is held constant in the optimization. Setting ∂L/∂p_i = 0 gives

$$k_{\tau }\sum _{k\in N}{H}_{ik}{p}_k+k_p{w}_i(p_i-p_{0i})+\sum _{k\in I\cup B}{K}_{ki}{\lambda }_k=k_{\tau }\sum _{j\in S}{\tau }_{0j}{c}_j{M}_{ji}{\ell }_j,i\in N$$ (11)

where

$$H_{ik}=\sum _{j\in S}{c}_j^2{M}_{ji}{M}_{jk}{\ell }_j.$$ (12)

Setting ∂L/∂λ_i = 0 recovers equation (7). Equations (7) and (11) form a square linear system with unknowns p_i and λ_i, which can be solved using standard methods.

Target pressures and shear stresses

In this approach, the target pressures at each node and target shear stresses in each segment are assumed to be constants or functions of other variables in the computation. The assumed values may be obtained from observations of hemodynamic characteristics in sub-regions of the experimental preparation accessible to direct measurement, e.g. by intravital microscopy, or derived from experimental estimates and/or empirical correlations in similar experimental systems. Prior information about values of pressures and shear stresses in the specific network under consideration is not required.

In the simulations presented here, networks derived from morphological data from the rat mesentery are considered [19]. Two approaches for setting the magnitudes of the target wall shear stresses in these networks are examined. The first approach is to use a fixed value for all segments. In this tissue, the frequency distribution of segment pressures, considering all vessel types (arterioles, venules and capillaries), has a maximum at ~ 21 mmHg (see Figure 1A of [19], relative pressure ~ 0.1). The average wall shear stress for segments with this pressure is ~ 15 dyn/cm² [18]. Therefore, a target value |τ_0j| = 15 dyn/cm² was used. For one network, further simulations were carried out to test the sensitivity of the results to this value.

The second approach is based on experimental observations and simulations of blood flow in microvascular networks that showed a systematic trend of increasing wall shear stress with increasing intravascular pressure [18]. This trend was attributed to the structural adaptation of microvessels in response to hemodynamic stimuli. Specifically, it has been observed that increased wall shear stress results in active remodeling of the vessel wall to increase vessel lumen diameter, whereas increased pressure causes inward remodeling of the vessel wall and a reduction in lumen diameter. The combined effect of these two responses is considered to underlie the observed correlation between pressure and shear stress [21]. The target shear stress was calculated as a function of the actual midpoint pressure p_j in each segment, using the empirical pressure-shear relationship observed in mesenteric microvascular networks [18]:

$$\left|{\tau }_{0j}\right|=100-86·exp\left\{-5000·{\left[log\left(log{p}_j\right)\right]}^{5.4}\right\},$$ (13)

where shear stress and pressure are expressed in units of dyn/cm² and mmHg, respectively. Because the target values |τ_0j| depend on the current values of the segment midpoint pressures p_j, an iterative procedure was used in which segment pressures p_j were estimated based on a given set of |τ_0j|, and then |τ_0j| were updated according to equation (13).

The target pressure is set to a fixed value in all segments, p_0k = p₀ = 31 mmHg, which is the average of the feeding and draining pressures of rat mesenteric networks [19]. The term proportional to k_p in the objective function L biases the node pressures towards this value. The results of the procedure depend on k_p and k_τ only through their ratio, and k_p was arbitrarily set to 0.1. In practice, k_τ/k_p > 1, and so the bias of node pressures towards p₀ is relatively small. Nonetheless, this term is necessary to constrain the nodal pressures to lie in a realistic range. For one network, additional simulations were carried out to test the sensitivity of the results to the target pressure.

Since the flow directions in the network are not known a priori, it is necessary also to specify the direction (sign) of the target wall shear stress in each segment. In principle, this could be done by performing the optimization over all possible choices of target directions, but this is not feasible for networks with hundreds or thousands of segments. Therefore, the following heuristic strategy was employed. Initial flow directions were chosen randomly, and an optimization was performed with a very small value (10⁻⁴) of the weight k_τ associated with the shear stress term in the objective function, with |τ_0j| set to a constant value (5 dyn/cm²). The resulting set of pressures and flow directions was used to re-assign τ_0j in each segment, with the sign of τ_0j corresponding to the last computed flow direction. This process was then repeated until two consecutive iterations gave the same flow directions in all segments. The value of k_τ was then doubled, and the flow directions from the previous iteration were used to determine τ_0j for this new k_τ value. The above process was then carried out iteratively for a sequence of geometrically increasing values of k_τ. The final shear stress weight, k_τ,final, was chosen to minimize the number of segments for which predicted flow directions were opposite to observed flow directions.

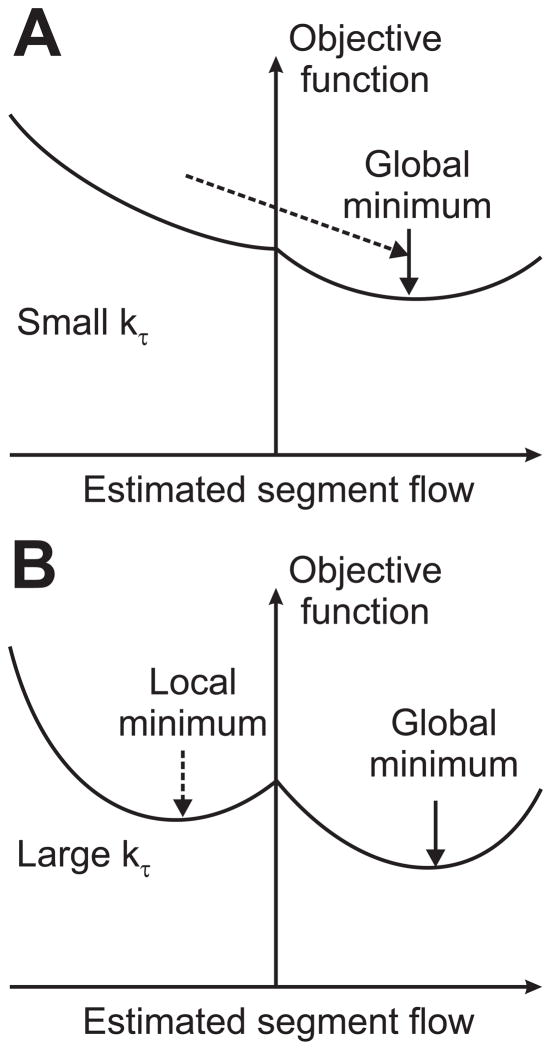
The rationale for this procedure is that if k_τ were set to k_τ,final at the outset, without this iterative procedure, the flow directions would be strongly biased to the initial, randomly assumed directions and would not readjust to achieve a lower overall error, due to the large weight of k_τ relative to k_p. However, when k_τ is set initially to a small value, the bias towards the initially assigned flow directions is small, allowing changes in flow directions (Figure 2). With increasing k_τ, flow directions eventually stabilize, having achieved better estimates (i.e., lower values of L) than would be achieved by simply fixing a k_τ value. This process is analogous to the well-known optimization technique of simulated annealing [7].

Figure 2.

Schematic illustration of optimization algorithm. The two graphs represent the dependence of the objective function on flow rate in one segment of the network. The objective function consists of a component dependent on the flow direction and a component independent of the flow direction but dependent on the deviation of the shear stress from the target value. A. When k_τ is small, the flow directions can change readily, such that the objective function can approach the global minimum. B. As k_τ increases, the flow directions become fixed according to the result at preceding optimizations with smaller values of k_τ, but the flow rates are increasingly determined by the minimization of the deviation of shear stress from the target value.

RESULTS

Identification of flow directions, estimation of k_τ,final

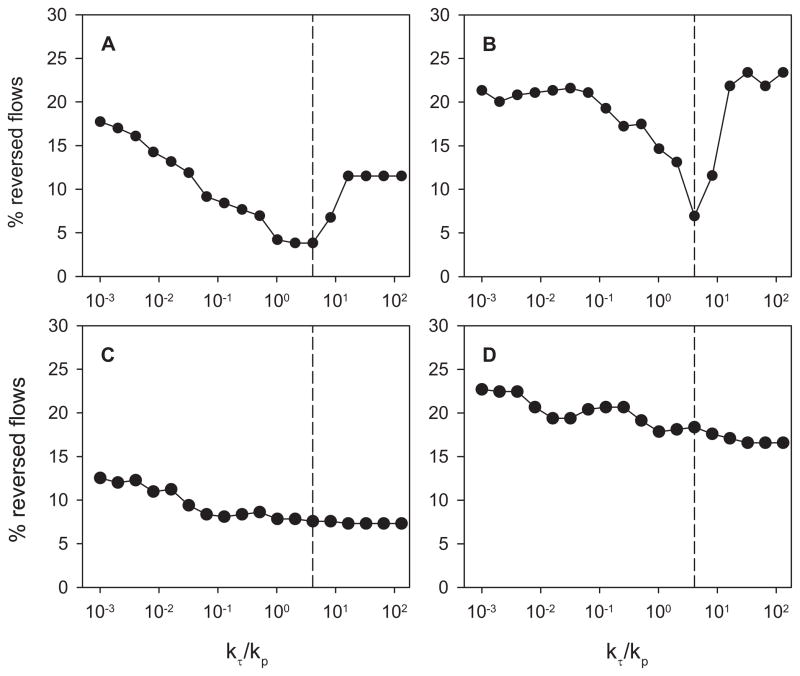
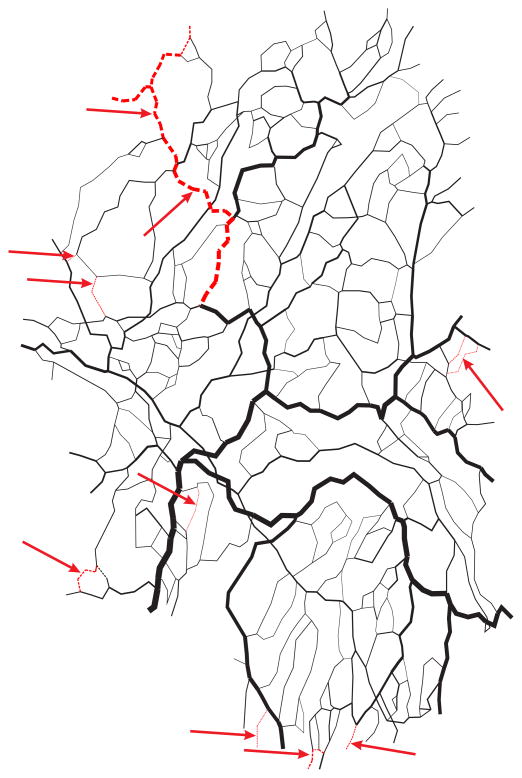
The model was tested using experimental data from four networks of the rat mesentery, for which flow rates were previously measured in all segments [22]. In these networks, the number of segments ranged from 383 to 547, and the number of boundary conditions ranged from 22 to 40. In the initial testing of the method, two boundary conditions were prescribed in network I, for the main feeding arteriole and the main draining venule. In networks II, III and IV, two main venules drained the network and three boundary conditions were therefore prescribed, for the main arteriole and the two main venules. In each case, the remaining boundary conditions were left unknown. In networks I and II, the number of reversed segments reached a minimum near k_τ = 0.4096, while in the other two networks, no clear minimum was reached (Figure 3). These results were obtained using a fixed target wall shear stress, 15 dyn/cm². Based on these results, the final shear stress weight was set to k_τ,final = 0.4096 in all four networks. With this value, the algorithm gave an average of 9.2% of the segments with predicted flow directions reversed (incorrect) relative to the flow directions obtained when the correct boundary conditions were applied to all boundary nodes. These results are summarized in Table 1. For one of the networks (number I), the segments with reversed flows are identified in Figure 4. In this network containing 547 segments, with 2 of 36 boundary conditions specified, the algorithm resulted in incorrect flow directions in a total of 28 segments, including only 5 of the remaining 34 boundary segments. Many of the segments with reversed flow lie near the boundaries of the network. This is to be expected, because the flow in a segment near the boundaries is sensitive to a few unknown boundary conditions. Flow in a segment far from the boundaries depends on many boundary conditions, and is therefore not as sensitive to errors in individual boundary conditions.

Figure 3.

Dependence of the number of reversed flows on the weighting factor k_τ for shear stress in the optimization. A general trend towards reduction in number of reversed flows was found as k_τ was sequentially increased. However, this trend was reversed at large values of k_τ in two networks. The vertical dashed line corresponds to k_τ = 0.4096, the value used in the subsequent application of the method. A. Network I. B. Network II. C. Network III. D. Network IV.

Table 1.

Percentage of reversed flows in mesenteric networks when two or three boundary conditions are specified.

Network	Network reference number	Number of segments	Number of boundary conditions	Number of specified boundary conditions	Percentage of reversed flows (%)
I	2810	547	36	2	3.8%
II	1502	389	22	3	6.9%
III	1008	383	22	3	7.6%
IV	1508	392	40	3	18.4%
Average					9.2%

Figure 4.

Computer-generated map of network I. Flow directions predicted with two known boundary conditions are compared with flow directions with all boundary conditions known. Black: correct flow direction. Red: reversed flow direction.

Estimation of flows and pressures

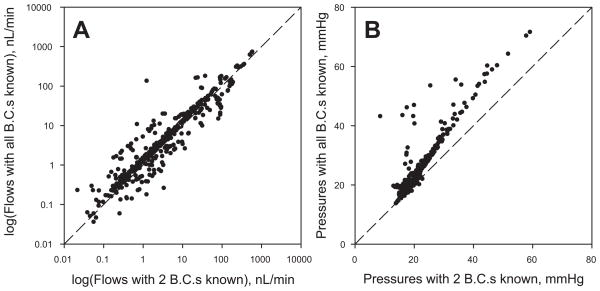
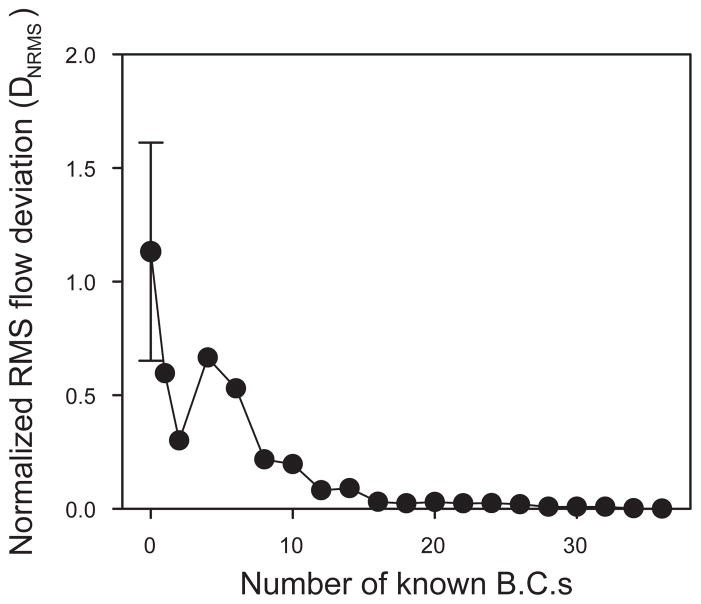
The segment flows and nodal pressures predicted for network I with two specified boundary conditions are compared in Figure 5 with the corresponding estimates with all boundary conditions specified. The results for the two sets of estimates are strongly correlated, although large discrepancies exist in a relatively small subset of the segments. These results suggest that the flow distributions estimated by this technique would provide a good basis for estimation of functional properties of the networks, such as parameters associated with transport of oxygen and other solutes. Figure 6 shows the effect of increasing the number of known boundary conditions on the normalized root mean square deviation (D_NRMS) between segment flows predicted with partial boundary information (Q_j) and those predicted when all boundary conditions are known (Q_j0), defined as

Figure 5.

Node pressures and segment flows in each segment of network I. Values predicted with two known boundary conditions are plotted against values with all boundary conditions known. A. Log(flows). B. Node pressures.

Figure 6.

Normalized root mean squared deviation in segment flows (D_NRMS), plotted as a function of the number of known boundary conditions for network I. In the case of one known boundary condition, the pressure at the main venular outflow is imposed. Flow boundary conditions are then successively added in order of decreasing flow magnitude. The error bars show the standard deviation of 6 results with different randomized starting conditions. The starting conditions had negligible effects if one or more boundary conditions were specified.

$$D_{\mathit{NRMS}}={\left[\sum _{j\in S}{(Q_j-Q_{j0})}^2/\sum _{j\in S}{Q_{j0}}^2\right]}^{1/2}$$ (14)

Boundary conditions were successively imposed in order of decreasing magnitude of observed flow. As would be expected, D_NRMS approaches zero as more boundary conditions are specified.

To test the dependence of the results on the randomly chosen initial flow directions, we performed simulations with 6 different randomized starting conditions, for network I. The results with zero boundary conditions specified showed large variations (Figure 6), but with one or more boundary conditions specified, the results were essentially independent of the assumed starting conditions. We also computed results corresponding to Figures 5A and 6 for red blood cell fluxes. The results (not shown) were essentially indistinguishable from those for blood flow rate.

Sensitivity of results to assumed target values

The computations described above were repeated using a pressure-dependent target wall shear stress |τ_0j| in each segment, according to equation (13). The results (not shown) did not differ significantly from those obtained using |τ_0j| = 15 dyn/cm² for all segments. Using a fixed target |τ_0j| is simpler and requires less detailed hemodynamic information, and is therefore preferable. When the simulation was repeated for network I with |τ_0j| = 30 dyn/cm², the number of incorrect flow directions and D_NRMS with two boundary conditions specified were almost doubled. This indicates that |τ_0j| is an important parameter in the method. Increasing the target pressure p_0k from 31 to 41 mmHg did not significantly change the number of incorrect flow directions or D_NRMS. However, decreasing p_0k to 21 mmHg led to a large increase in both the number of incorrect flow directions and D_NRMS.

DISCUSSION

Methods for imaging the three-dimensional structure of microvascular networks have advanced in recent years. However, the interpretation of the results of such studies in terms of the functional properties of the microvasculature remains a challenge to be addressed. Basic morphological measures such as vascular length density, vascular volume fractions or vessel-vessel spacing provide very limited information about the ability of a network to perfuse a tissue and to deliver an adequate supply of oxygen and other nutrients. Networks with similar values of these parameters may nonetheless have entirely different functional characteristics because of different connectivity or diameter distributions. For example, in tumor networks, high levels of perfusion and vascular density may coexist with significant tissue hypoxia because of functional shunting of blood flow through short pathways [15]. Ideally, assessment of microcirculatory function should thus be based on information on both structure and flow distribution. However, detailed flow information is technically difficult to obtain in many cases of interest.

The theoretical method presented in this study is intended to address this lack of experimental information. In this method, the distribution of flows in a network is computed based on (i) known physical principles governing blood flow in microvascular networks; (ii) limited information about the flows or pressures at a few major vessels feeding and draining the network; and (iii) independently derived empirical information about the distributions of pressures and flows in the network. The algorithm uses a constrained optimization approach to generate estimates of segment flows based on this incomplete information. These estimates are shown to correlate well with the results obtained when full information on boundary conditions is available. In some of the networks considered, blood flow velocities were previously measured experimentally and flow rates were estimated [19, 23]. While these estimates could in principle be used as an alternative standard for comparison with the results of the present method, they are subject to experimental errors [23], leading to significant violation of flow conservation at bifurcations. Consequently, the simulation cannot possibly reproduce the experimentally observed flow rates. The goal of the algorithm is to estimate segment flow rates in the absence of a full set of boundary conditions. Therefore, the appropriate standard of comparison is the computed flow distribution with all boundary conditions known.

In this method, the role of the target shear stress and pressure is to ensure that these parameters are in physiologically realistic ranges throughout the network, not to force shear stresses and pressures in each vessel to match the target values. The computed flows imply wide distributions of shear stress and pressure in the network.

It must be recognized that this method has significant limitations. It represents an attempt to solve a system that is mathematically underdetermined when constrained by the available data. Therefore, the results are inevitably approximate. Despite good overall agreement between results from this approach and the ‘true’ values, significant errors are obtained for a subset of segments in the network. These errors decline as the number of known boundary conditions is increased. The method depends on the availability of independent information on distributions of pressures and wall shear stresses in the type of network under consideration. In the examples considered here, such information is available because of the suitability of mesenteric networks for study by intravital microscopy. In other tissues, such data are more difficult to obtain. While data from one tissue, such as mesentery, may be applicable to other tissues, this approach may neglect systematic differences between the microcirculation of different tissues. For example, tumors exhibit systematic differences from normal tissues, as already mentioned. Finally, the algorithm is computationally intensive: hundreds of solutions to the network flow problem must be computed as part of the optimization procedure. When applied to networks containing hundreds of segments, the algorithm takes a few minutes to run on a standard personal computer.

The algorithm does not require a priori information about whether vessels are arterioles, capillaries or venules. If vessel types are known, such that flow directions can be specified in advance in some vessels, then the model can readily be modified to take this into account, by fixing the sign of the target shear stress in such vessels.

In conclusion, the method presented here enables the estimation of blood flows in all segments of a microvascular network, given incomplete information about flow or pressure in the boundary segments, together with independent estimates or correlations describing distributions of pressure and wall shear stress in the tissue under consideration. Structural information in combination with flow information allows detailed simulations of transport of oxygen and other solutes [24]. Therefore, we anticipate that this method will assist in the interpretation of data obtained from three-dimensional imaging of microvascular networks containing large numbers of segments, and will potentially lead to new insights into functional properties of the microcirculation in various tissues under a range of conditions.