Microtubule Capture by Mitotic Kinesin Centromere Protein E (CENP-E)

Background: CENP-E is a processive kinesin that is required for chromosome congression and stable chromosome biorientation.

Results: CENP-E exhibits unusually slow microtubule collision coupled with slow ADP release.

Conclusion: This novel ATPase cycle may favor CENP-E binding of stable kinetochore microtubules over dynamic microtubules.

Significance: This study may enhance our understanding of the role of CENP-E in mitosis and meiosis.

Abstract

Centromere protein E, CENP-E, is a kinetochore-associated kinesin-7 that establishes the microtubule-chromosome linkage and transports monooriented chromosomes to the spindle equator along kinetochore fibers of already bioriented chromosomes. As a processive kinesin, CENP-E uses a hand-over-hand mechanism, yet a number of studies suggest that CENP-E exhibits mechanistic differences from other processive kinesins that may be important for its role in chromosome congression. The results reported here show that association of CENP-E with the microtubule is unusually slow at 0.08 μm⁻¹ s⁻¹ followed by slow ADP release at 0.9 s⁻¹. ATP binding and hydrolysis are fast with motor dissociation from the microtubule at 1.4 s⁻¹, suggesting that CENP-E head detachment from the microtubule, possibly controlled by phosphate release, determines the rate of stepping during a processive run because the rate of microtubule gliding corresponds to 1.4 steps/s. We hypothesize that the unusually slow CENP-E microtubule association step favors CENP-E binding of stable microtubules over dynamic ones, a mechanism that would bias CENP-E binding to kinetochore fibers.

Introduction

Accurate chromosome segregation requires that sister kinetochores on each chromosome establish stable attachments to opposite spindle poles by microtubules (MTs)² (reviewed in Ref. 1). This process of biorientation is mediated by MT bundles or k-fibers attached to the sister kinetochores of each chromosome (2). CENP-E is a mitotic kinesin whose expression is up-regulated during G₂ and M phases of the cell cycle, and it localizes to kinetochores from early prometaphase through metaphase moving to the antiparallel midzone MTs at anaphase (3–7). CENP-E is well conserved throughout the animal kingdom, and reduced levels of CENP-E in cells and mice have been linked to aneuploidy and chromosome instability (8–10). In 2006, Kapoor et al. (11) made the remarkable discovery that chromosomes can congress to the spindle equator prior to biorientation through a novel mechanism in which monooriented chromosomes glide to the metaphase plate along kinetochore MTs (kMTs) of chromosomes that were already bioriented (11, 12). Their results revealed that this movement of monooriented chromosomes was dependent upon CENP-E.

CENP-E is an N-terminal homodimeric kinesin that promotes slow processive MT plus-end-directed movement (13, 14) like conventional kinesin-1 (15–17) and kinesin-5 Eg5/kinesin-5 Eg5/KSP (18). CENP-E processive run lengths have been reported at 1.5–2.6 μm with the rate of stepping varying from 8 to 342 nm/s, depending on the specific construct expressed and the surface conditions of the assay (13, 14, 19–21). The stall force for CENP-E at 6 piconewtons is comparable with the stall force of kinesin-1 (14), and Rosenfeld et al. (22) reported that CENP-E exhibits a kinetics profile similar to kinesin-1 where ATP binding to the lead head was gated by intramolecular strain such that ATP binding on the leading head can only occur once strain is relieved by detachment of the trailing head. Comparative studies of processive kinesins revealed that neck linker length, sequence, and orientation modulate interhead tension and therefore regulate head-head communication for processive stepping (17, 21, 23). However, unlike kinesin-1 and Eg5, CENP-E can also promote MT plus-end elongation in vitro (20), suggesting that the mechanochemistry of CENP-E is specific for its functional roles in mitosis.

More recently, a key threonine residue near the CENP-E motor domain and conserved across species (Thr⁴²² in human and Thr⁴²⁴ in Xenopus laevis) has been identified as the site of a phospho-regulatory switch that is critical for chromosome congression and correct biorientation (24). Phosphorylation of this threonine by Aurora kinases A and B occurs during prometaphase when the chromosomes are near the spindle poles and where the gradient of Aurora kinases is high. Because CENP-E phosphorylation weakens its affinity for MTs, this mechanism is believed to contribute to correction of inappropriate kinetochore MT attachments. In contrast, as chromosomes move away from the spindle poles and congress to the equator, CENP-E becomes dephosphorylated by protein phosphatase 1, leading to higher MT affinity and stabilization of kinetochore end-on kMT amphitelic attachments (24, 25).

To identify mechanistic differences for CENP-E that contribute to its role in chromosome congression, we pursued a pre-steady-state kinetics study using a recombinant, truncated human CENP-E dimer (20). The results show that the ATPase mechanism accounts for the high processivity of CENP-E and its ability to elongate MTs in vitro. More importantly, this study has revealed that productive CENP-E association with the MT is unusually slow and may bias CENP-E selection for stable kMTs, a characteristic that could enhance the role of CENP-E in chromosome congression.

EXPERIMENTAL PROCEDURES

Experimental Conditions

The experiments reported in this study were performed at room temperature (22–25 °C) in ATPase buffer (20 mm Hepes, pH 7.2 with KOH, 5 mm magnesium acetate, 0.1 mm EDTA, 0.1 mm EGTA, 50 mm potassium acetate, 1 mm dithiothreitol, and 5% sucrose). On the morning of each experiment, bovine brain tubulin was cold-depolymerized, clarified, and polymerized with 1 mm GTP at 34 °C. These MTs were stabilized with 40 μm paclitaxel, and MT concentrations reported are the paclitaxel-stabilized tubulin polymer. All reported concentrations of nucleotides (ATP, ADP, GTP) and nucleotide analogues (mantATP, mantADP, AMPPNP, ATPγS) also include the equivalent concentration of magnesium acetate. Errors are reported as S.E.

Purification of CENP-E and Tubulin Proteins

A human CENP-E construct was expressed in Escherichia coli and purified as described previously (20). The CENP-E-His₆ protein includes the N-terminal residues, Met¹–Leu⁴⁰⁷, followed by 22 additional residues at the C terminus from the pET30c(+) plasmid (RDPNSSSVDKLAAALEHHHHHH). The predicted M_r is 48,467 per polypeptide chain and 96,934 for the CENP-E dimer. On the day of each experiment, CENP-E was clarified (90,000 rpm for 5 min at 4 °C, Beckman Coulter Optima TLX ultracentrifuge, TLA 100 rotor) followed by protein concentration determination using the Bio-Rad protein assay with IgG as the standard. The CENP-E concentration is reported based on the concentration of a single CENP-E polypeptide.

Formation of the Nucleotide-free MT·CENP-E Complex

For the experiments in Figs. 1 and 4, the MT·CENP-E complex was preformed and treated with apyrase (0.02 unit/ml; grade VII, Sigma-Aldrich) for 20 min to generate a nucleotide-free complex (26, 27). The grade VII apyrase isoform preferentially selects ADP to convert to AMP, and the binding affinity of AMP for CENP-E is so weak that CENP-E becomes essentially nucleotide-free. Because the concentration of apyrase used is so low, it does not compete with CENP-E for nucleotide during the experiments.

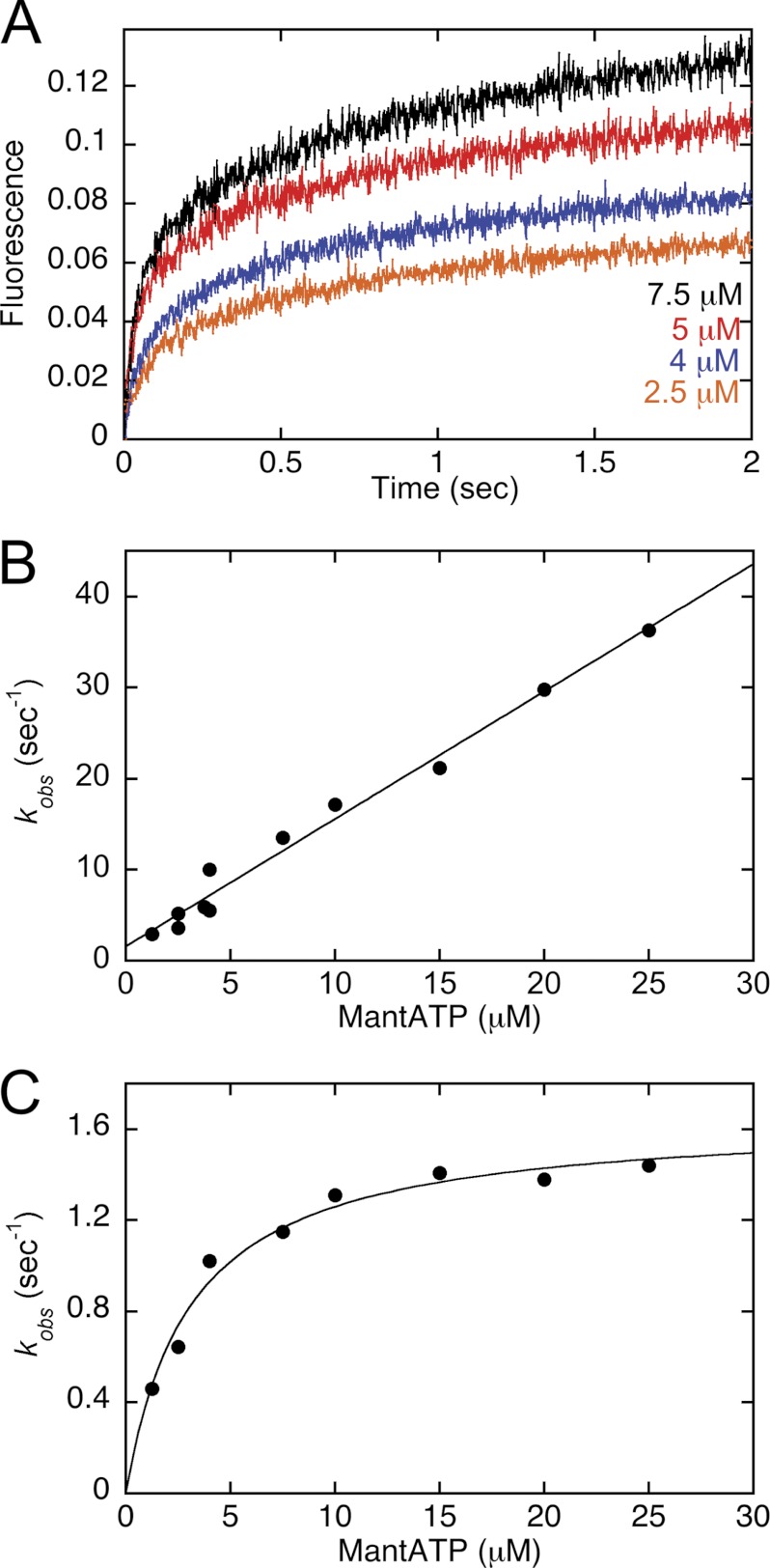
FIGURE 1.

MantATP binding kinetics. The nucleotide-free MT·CENP-E complex was rapidly mixed in the stopped-flow instrument with increasing concentrations of mantATP. A, representative transients at 2.5, 4, 5, and 7.5 μm mantATP (bottom to top) show an exponential increase in fluorescence as a function of time. Final concentrations: 2.5 μm CENP-E, 7.5 μm MTs. B, the observed rates of the initial exponential phase were plotted as a function of mantATP concentration, and the linear fit of the data provided k₊₁ = 1.4 ± 0.06 μm⁻¹ s⁻¹ and k₋₁ = 1.6 ± 0.7 s⁻¹. C, the observed rates of the second exponential phase were plotted as a function of mantATP concentration, and the hyperbolic fit of the data provided k_max = 1.6 ± 0.06 s⁻¹ and K½_,mantATP = 3.1 ± 0.4 μm. Final concentrations: 2.5 μm CENP-E/7.5 μm MTs for 1.25–7.5 μm mantATP and 4 μm CENP-E/7.5 μm MTs for 2.5–25 μm mantATP.

FIGURE 4.

ATP-triggered mantADP release kinetics. A preformed MT·CENP-E·mantADP (mADP) complex was rapidly mixed in the stopped-flow instrument with ATP. Final concentrations: 5 μm CENP-E, 10 μm MTs, 2 μm mantATP (mATP), 5–500 μm ATP. A, experimental design to establish the processive stepping intermediate. B, representative transients at 0, 10, 25, 50, 100 μm ATP (top to bottom). C, the observed rates of the initial exponential phase were plotted as a function of ATP concentration, and the hyperbolic fit of the data provided k_max = 19.4 ± 0.6 s⁻¹, K½_,ATP = 26.6 ± 3.2 μm.

Kinetics of mantATP Binding

The nucleotide-free MT·CENP-E complex was rapidly mixed with mantATP (Invitrogen Molecular Probes) in a KinTek SF2003 stopped-flow instrument, and the fluorescence change was monitored (λ_ex = 360 nm, λ_em = 450 nm, 409-nm long pass filter). The fluorescence increase as a function of time is correlated with mantATP binding because the fluorescence of mantATP is enhanced by the hydrophobic environment of the active site. Each transient was fit to a double exponential function, the observed rate of the initial exponential phase was plotted as a function of mantATP concentration, and the data were fit to the following equation

where k_obs represents the observed rate of the initial exponential phase, k₊₁ is the second-order rate constant for mantATP binding, and k₋₁ is the dissociation rate constant obtained from the y-intercept (see Fig. 1).

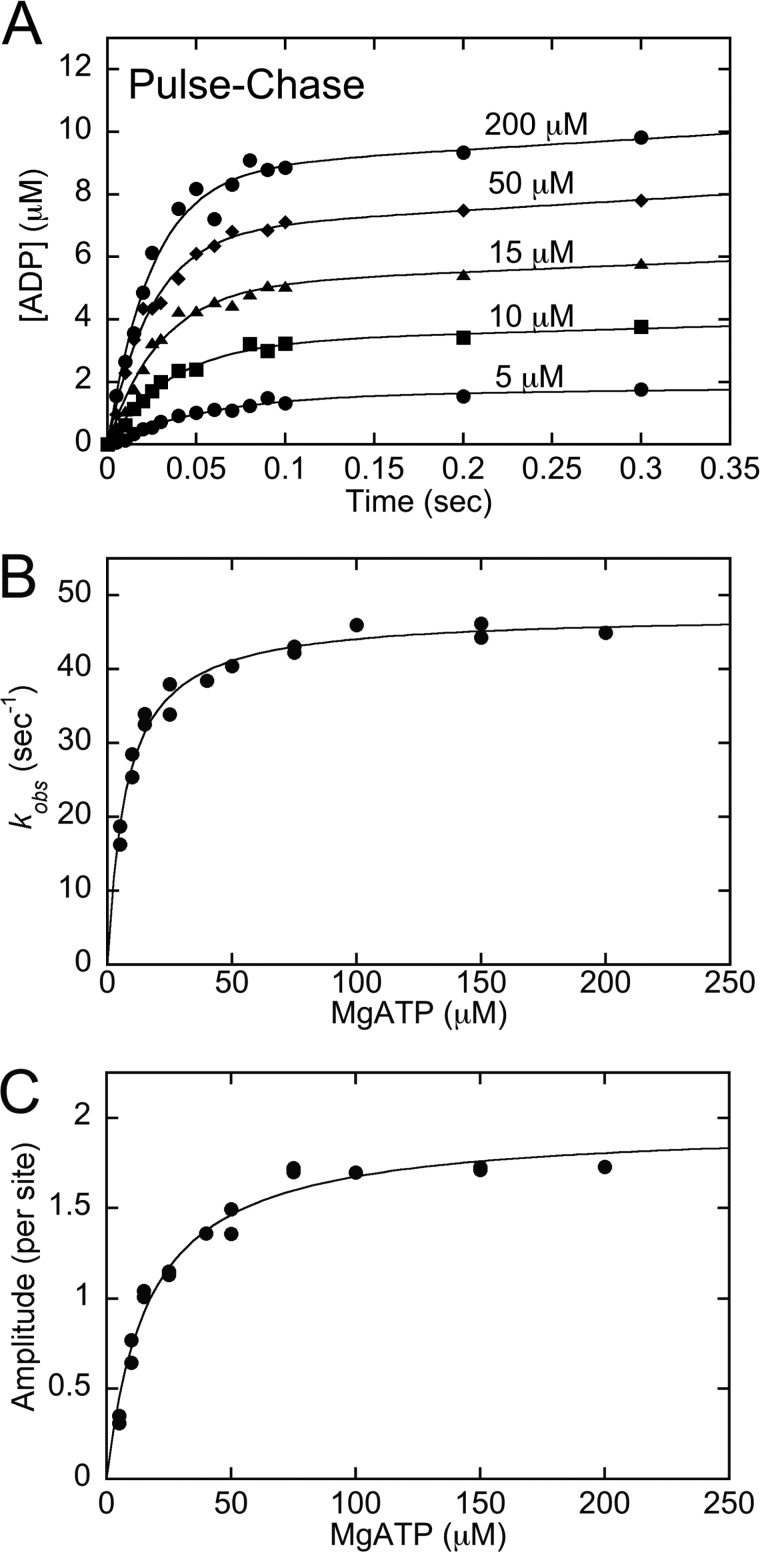
Pulse-Chase Kinetics of ATP Binding

The MT·CENP-E complex was preformed and rapidly mixed in the KinTek chemical quench-flow instrument with ATP plus trace [α-³²P]ATP. The reaction was subsequently chased with 30 mm nonradiolabeled ATP (syringe concentration) and allowed to proceed for 15 s (>10 turnovers). The reaction was expelled from the instrument into a 1.5-ml tube containing 100 μl of 22 n formic acid. The acid terminates the reaction and releases any nucleotide at the active site. This experimental design quantifies [α-³²P]ATP stably bound at the active site because during the time of the chase, the stably bound [α-³²P]ATP proceeds through ATP hydrolysis. Any weakly bound [α-³²P]ATP or [α-³²P]ATP in solution is diluted by the high concentration of nonradiolabeled ATP. Therefore, this experiment measures the kinetics of ATP binding. The products [α-³²P]ADP + P_i were separated from [α-³²P]ATP by thin layer chromatography and quantified (27, 28). The individual transients were fit to the following burst equation

where A₀ is the amplitude of the initial exponential burst phase representing the concentration of ADP·P_i formed at the active site during the first ATP turnover, k_b is the observed rate of the exponential burst phase, k_slow represents the rate of subsequent ATP binding events corresponding to steady-state turnover, and t is the time in seconds. For these experiments, 200 mm KCl was added to the [α-³²P]ATP syringe, resulting in a final concentration of 100 mm KCl after mixing and prior to the unlabeled ATP chase. This strategy is commonly used for processive kinesins to slow the rate of subsequent ATP turnovers without affecting the first turnover (27, 29–34). The exponential burst phase therefore becomes better defined to quantify the kinetics of the first ATP turnover.

The observed rates of the initial exponential burst phase were plotted as a function of ATP concentration, and the data were fit to the following equation

where K₁ represents the equilibrium association constant for formation of the collision complex, and k₊₁′ is the first-order rate constant for the ATP-promoted isomerization with K_d = 1/K₁ (see Fig. 2).

FIGURE 2.

Kinetics of ATP binding by pulse-chase. The MT·CENP-E complex was rapidly mixed with increasing concentrations of [α-³²P]ATP + KCl in a chemical quench-flow instrument followed by a nonradiolabeled ATP chase. Final concentrations: 5 μm CENP-E, 15 μm MTs, 5–200 μm [α-³²P]ATP, 100 mm KCl. A, representative transients show an exponential increase of [α-³²P]ADP·P_i product formation during the first ATP turnover followed by a linear phase of product formation. B, the observed rates of the initial exponential phase were plotted as a function of ATP concentration, and the fit of the data to Equation 3 provided K₁ = 0.13 ± 0.01 μm⁻¹, k₊₁′ = 47.5 ± 0.8 s⁻¹ with K₁k₊₁′ = 6.2 μm⁻¹ s⁻¹ and K_d,ATP = 7.7 μm. C, the amplitudes of the pre-steady-state exponential burst phase were plotted as a function of ATP concentration, and the hyperbolic fit of the data provided A_max = 1.96 ± 0.1 ADP·P_i/site with apparent K_d,ATP = 16.7 ± 1.7 μm. Data shown in panels B and C are from multiple experiments.

Acid Quench Kinetics

The pre-steady-state kinetic experiments to determine the time course of ATP hydrolysis were performed in the KinTek chemical quench-flow instrument as described (27, 28). The MT·CENP-E complex was rapidly mixed with ATP plus trace [α-³²P]ATP for times ranging from 5 to 600 ms. The ATP syringe also contained 200 mm KCl (100 mm after mixing). At varying times of incubation, the reaction was quenched with 10 n formic acid (syringe concentration). The formic acid quench terminated the reaction and unfolded the protein, releasing nucleotide from the active site. The products [α-³²P]ADP and P_i were separated from [α-³²P]ATP and quantified as described above for the pulse-chase experiments. The transients from these experiments were fit to Equation 2, and the observed rates of the initial exponential burst phase were plotted as a function of ATP concentration. The hyperbolic fit of the data provided the rate constant of ATP hydrolysis, k₊₂ (see Fig. 3).

FIGURE 3.

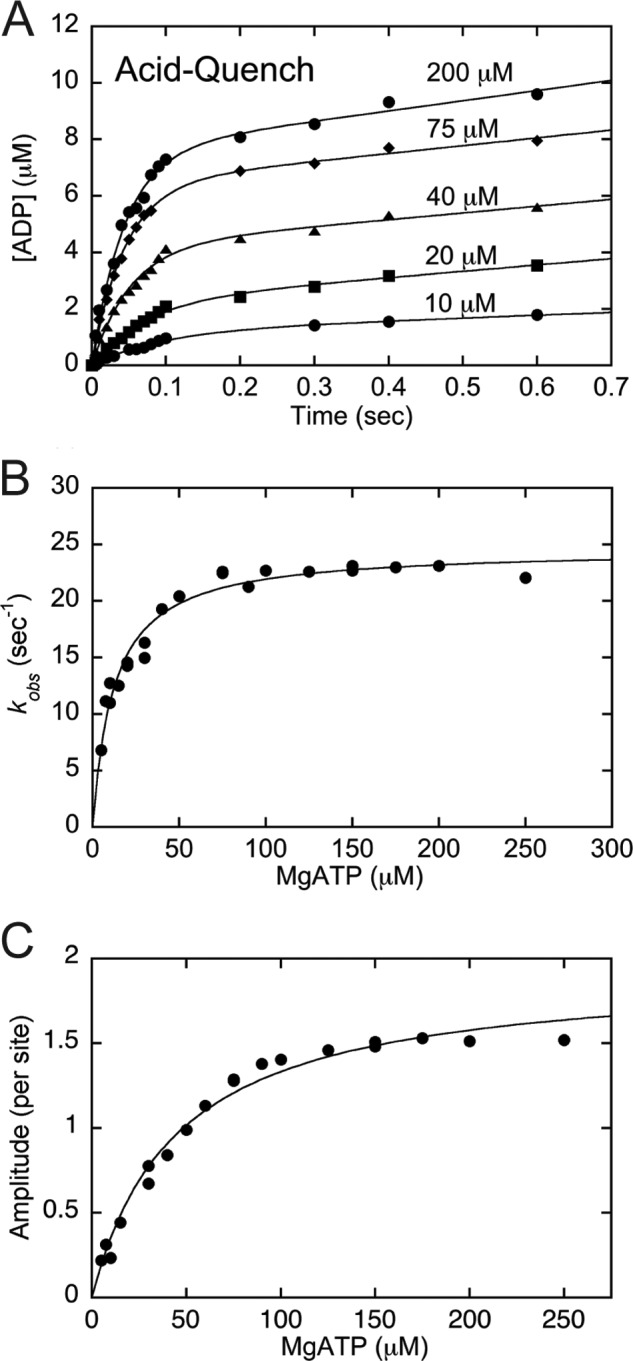
Kinetics of ATP hydrolysis by acid quench. The MT·CENP-E complex was rapidly mixed with increasing concentrations of [α-³²P]ATP in a chemical quench-flow instrument for 5–300 ms followed by a formic acid quench to terminate the reaction. Final concentrations: 5 μm CENP-E, 15 μm MTs, 5–200 μm [α-³²P]ATP, 100 mm KCl. A, representative transients show an exponential increase of [α-³²P]ADP·P_i product formation during the first ATP turnover followed by a linear phase of product formation. B, the observed exponential burst rates were plotted as a function of ATP concentration, and the hyperbolic fit of the data provided k₊₂ = 24.7 ± 0.5 s⁻¹ with K_d,ATP = 12.3 ± 1.1 μm. C, the amplitudes of the pre-steady-state exponential burst phase were plotted as a function of ATP concentration, and the fit of the data yields A_max = 1.93 ± 0.1 ADP·P_i/site with apparent K_d,ATP = 44.8 ± 4.4 μm. Data shown in panels B and C are from multiple experiments.

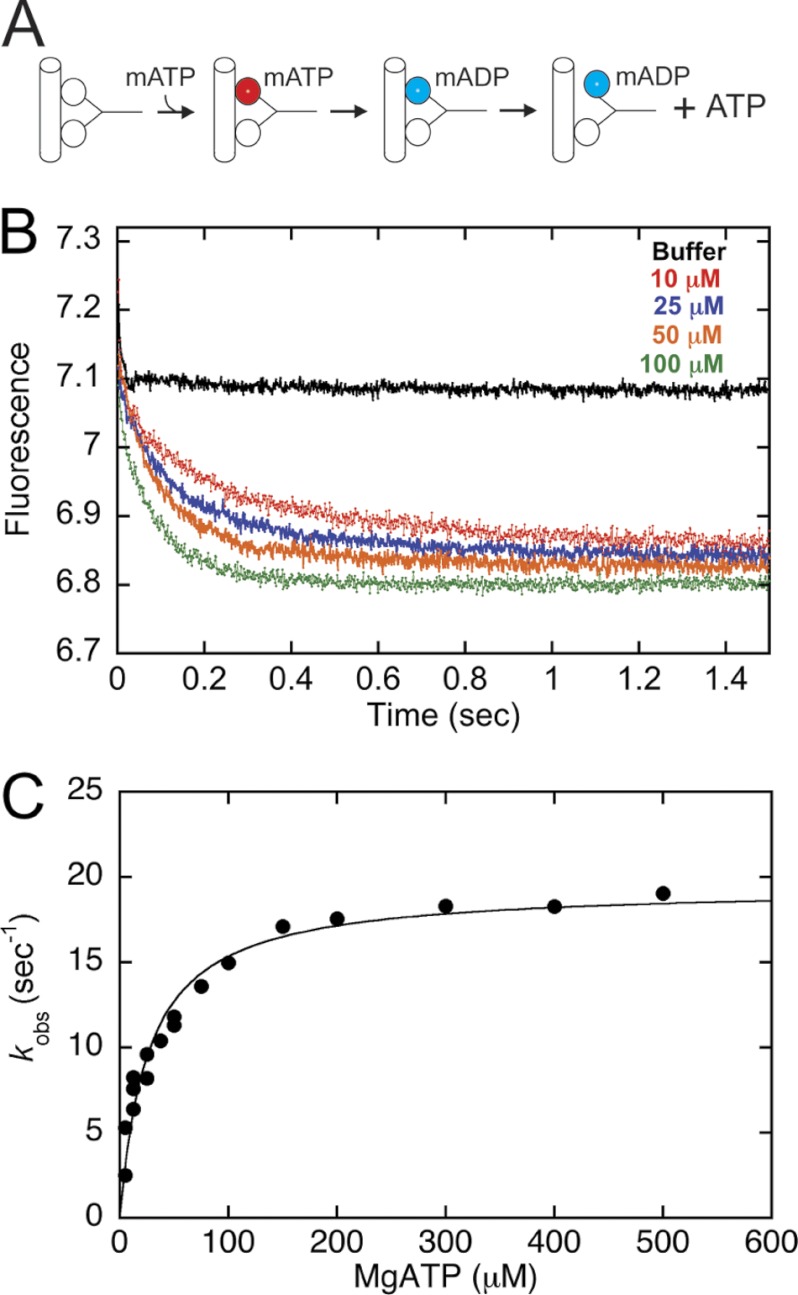
ATP-triggered mantADP Release

To determine the mantADP release kinetics from the trailing head (see Fig. 4) and correlated with processive stepping required that we generate an intermediate in which the leading head was nucleotide-free and tightly bound to the MT with the trailing head detached from the MT and mantADP tightly bound at its active site (see Fig. 4A). The strategy used was previously developed for Eg5 (26). The preformed MT·CENP-E complex (10 μm CENP-E, 20 μm MTs, syringe concentrations) was treated with apyrase to generate a nucleotide-free complex. This complex was incubated with 4 μm mantATP, a concentration less than half the CENP-E active sites, and therefore, each mantATP was assumed to bind to the nucleotide binding site of the trailing head because of strain-induced gating of the leading head (17, 22, 23, 32, 35). The mantATP was subsequently hydrolyzed to mantADP (see Fig. 4A). This MT·CENP-E·mantADP complex was then rapidly mixed with increasing concentrations of ATP in the stopped-flow instrument, and the fluorescence change over time was monitored and correlated with mantADP release from the active site. The observed exponential rates were plotted as a function of ATP concentration and fit to a hyperbolic function (see Fig. 4C).

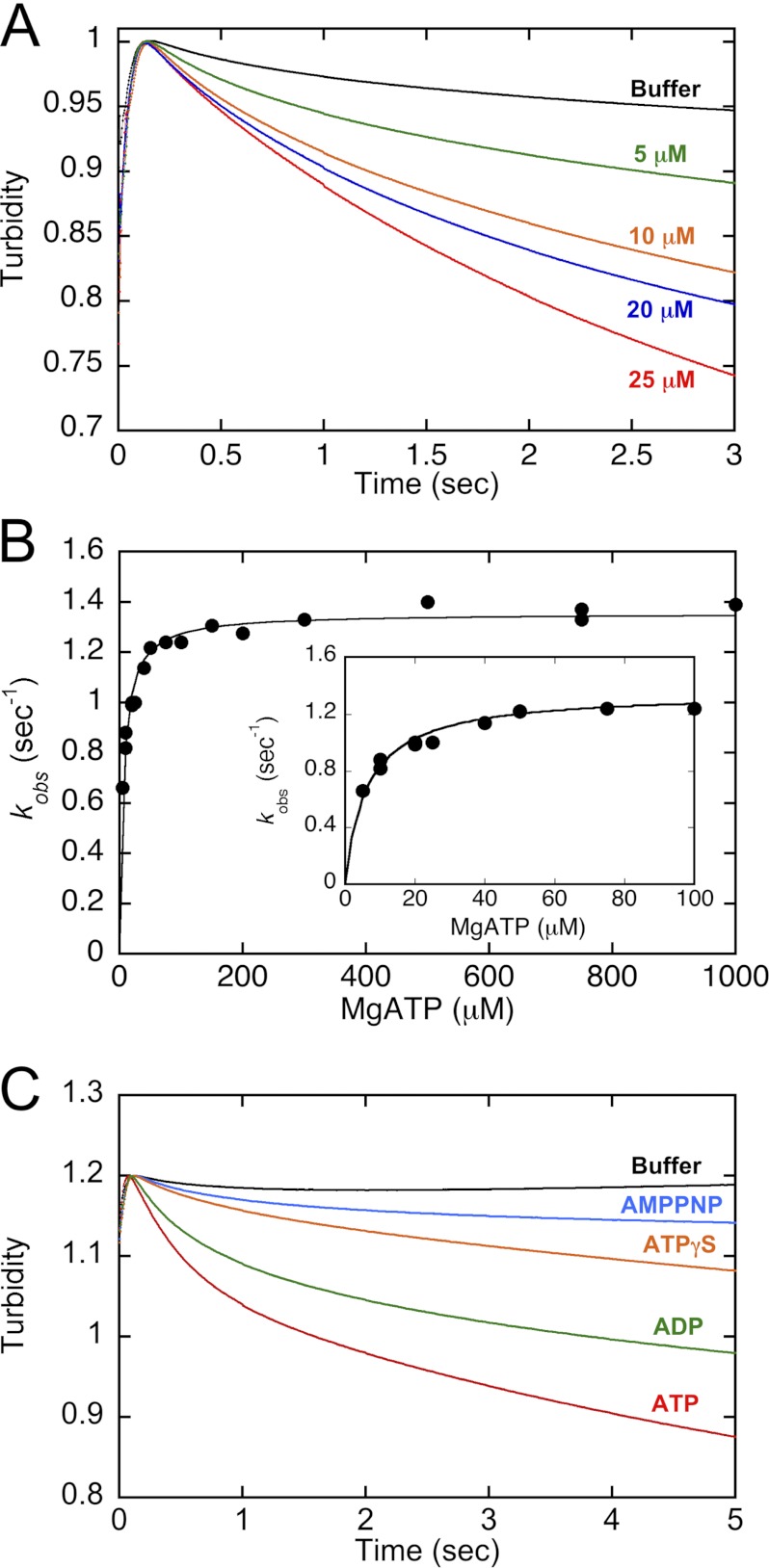
MT·CENP-E Dissociation Kinetics

The preformed MT·CENP-E complex was rapidly mixed in the stopped-flow instrument with increasing concentrations of ATP plus 300 mm KCl (syringe concentration), and turbidity (λ_ϵx = 340 nm) was monitored. Because the MT·CENP-E complex has a greater mass than MTs without motors or CENP-E in solution, the detachment of CENP-E from MTs results in a decrease in turbidity. The observed initial exponential rates from the transients were plotted as a function of increasing ATP concentration, and a hyperbolic fit of these data provided k₊₃, the rate constant of ATP-promoted CENP-E detachment from the MT (see Fig. 5).

FIGURE 5.

ATP-promoted dissociation kinetics of the MT·CENP-E complex. The preformed MT·CENP-E complex was rapidly mixed in the stopped-flow instrument with increasing concentrations of ATP plus KCl. Final concentrations: 4.5 μm CENP-E, 5 μm MTs, 0–1000 μm ATP, 150 mm KCl. A, representative transients show an exponential decrease in turbidity at 0, 5, 10, 20, 25 μm ATP. B, the observed rates of the exponential decreasing phase were plotted as a function of ATP concentration. The hyperbolic fit of the data provides k₊₃ = 1.4 ± 0.01 s⁻¹, K½_,ATP = 6.4 ± 0.5 μm. C, comparison of dissociation kinetics in the presence of buffer, AMPPNP, ATPγS, ADP, and ATP. Final concentrations: 4.5 μm CENP-E, 5 μm MTs, 1 mm nucleotide or analog, 150 mm KCl.

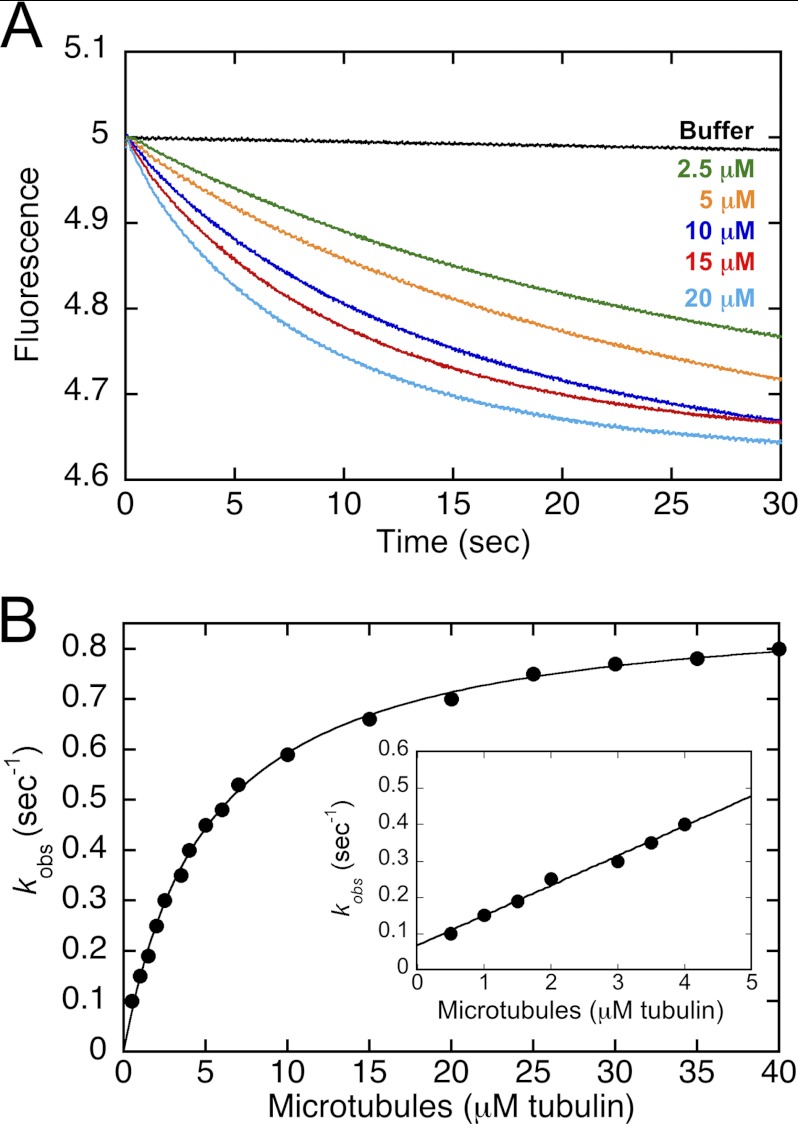
CENP-E MT Association Kinetics and Kinetics of mantADP Release after MT Collision

The stopped-flow instrument was used to measure the MT·CENP-E association kinetics and mantADP release kinetics (see Fig. 6). A CENP-E·mantADP complex was preformed and rapidly mixed in the stopped-flow instrument with varying concentrations of MTs plus 2 mm ATP (syringe concentration), and the fluorescence change was monitored over time. The transients were fit to a double exponential function, and the observed rates of the initial exponential phase were plotted as a function of increasing MT concentrations. The data from 0.5 to 4 μm were fit to the following linear equation

where k₊₄ is the second-order rate constant for MT association, and k₋₄ is the CENP-E off rate as defined by the y axis. The apparent K_d,MT is defined by k₋₄/k₊₄.

FIGURE 6.

MT association and mantADP release kinetics upon MT collision. The CENP-E·mantADP complex was preformed and rapidly mixed in the stopped-flow instrument with varying concentrations of MTs plus ATP. A, representative transients at 0, 2.5, 5, 10, 15, 20 μm tubulin polymer (top to bottom) reveal an exponential decrease in mantADP fluorescence as a function of time. Final concentrations: 2.5 μm CENP-E, 0–20 μm MTs, 15 μm mantADP, 1 mm ATP. B, the observed rates of the initial exponential phase were plotted as a function of MT concentration, and the hyperbolic fit of the data provided: k₊₅ = 0.9 ± 0.01 s⁻¹, K½_,MT = 5.1 ± 0.1 μm. Inset: at low MT concentrations, there is a linear increase in the observed rates of mantADP release, which represents the MT association kinetics because release of mantADP is limited by MT association at these low MT concentrations. The linear fit of the data provided the second-order rate constant k₊₄ = 0.08 ± 0.004 μm⁻¹ s⁻¹ with k₋₄ = 0.07 ± 0.01 s⁻¹. Final concentrations: 0.5 μm CENP-E for 0.5–1 μm MTs, 1 μm CENP-E for 2–7 μm MTs, 2.5 μm CENP-E for 2.5–40 μm MTs, 15 μm mantADP, 1 mm ATP.

MantADP Release from the CENP-E·mantADP Intermediate in the Absence of MTs

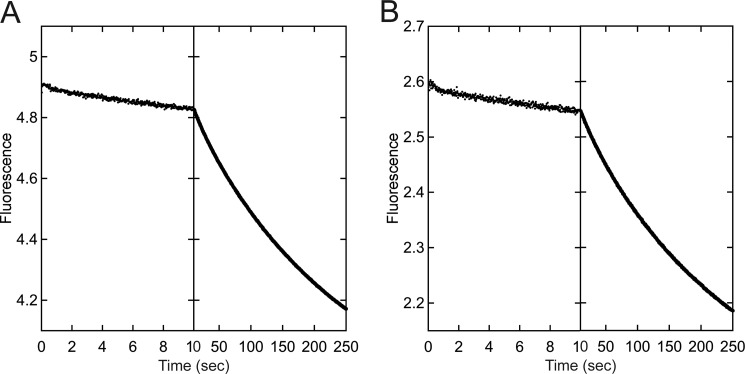
This experiment was designed to determine whether CENP-E bound ADP tightly at both nucleotide sites of the dimer, or whether the dimer exhibited a high affinity site and a low affinity site. Nucleotide-free CENP-E at 5 μm was incubated with either 5 μm or 2.5 μm mantADP to form the CENP-E·mantADP intermediate. It was assumed that if one nucleotide site bound mantADP tightly and the other weakly, the addition of 2.5 μm mantADP to 5 μm CENP-E would result in mantADP partitioning to the high affinity site. The CENP-E·mantADP intermediate was rapidly mixed in the stopped-flow instrument, and data were collected in two time domains: 1–10 and 10–250 s with fluorescence expressed in arbitrary units. Each transient was fit to a double exponential function (see Fig. 7).

FIGURE 7.

Kinetics of mantADP release from the CENP-E·mantADP intermediate. CENP-E·mantADP was rapidly mixed in the stopped-flow instrument with ATP, and the release of mantADP was observed at 1–10 and 10–250 s. Each transient was fit to a double exponential function. A, final concentrations: 2.5 μm CENP-E, 2.5 μm mantADP, 500 μm ATP. k_obs1 = 0.086 ± 0.003 s⁻¹ with A₀ = 0.046 ± 0.001, and k_obs2 = 0.004 ± 0.00004 s⁻¹ with A₀ = 1.02 ± 0.004. B, final concentrations: 2.5 μm CENP-E, 1.25 μm mantADP, 500 μm ATP. k_obs1 = 0.097 ± 0.005 s⁻¹ with A₀ = 0.025 ± 0.0007 and k_obs2 = 0.004 ± 0.00005 s⁻¹ with A₀ = 0.55 ± 0.002. Fluorescence is expressed in arbitrary units.

RESULTS

This study analyzed the ATPase cycle of a CENP-E dimeric motor (20). We showed previously that this CENP-E dimer promotes MT plus-end-directed MT gliding at 11 nm/s, and the steady-state ATPase k_cat was 0.9 s⁻¹. Furthermore, MT plus-end elongation promoted by CENP-E required ATP turnover, and the kinetics revealed that the elongation rate occurred at 1.03 αβ-tubulin subunits/s. The overall goal for the pre-steady-state kinetics study presented here was to determine whether the ATPase mechanism of CENP-E was consistent with its processivity, the CENP-E-promoted MT elongation, and whether the catalytic cycle was in some way tuned for its role in chromosome congression.

ATP Binding Is Rapid and Indicative of Alternating Head Catalysis

Substrate binding by dimeric CENP-E was measured by two approaches: fluorescent mantATP binding using the stopped-flow instrument (Fig. 1) and pulse-chase kinetics with [α-³²P]ATP using the rapid quench-flow instrument (Fig. 2). Fig. 1A shows representative transients of mantATP binding to the nucleotide-free MT·CENP-E complex at increasing concentrations of mantATP. The transients are biphasic, and the observed rates of the initial exponential phase were plotted as a function of mantATP concentration, providing the second-order rate constant of mantATP binding at 1.4 μm⁻¹ s⁻¹ (Fig. 1B, Table 1). The observation that the mantATP binding kinetics were biphasic (Fig. 1A) suggests that the second phase represents mantATP binding to the second head of the CENP-E dimer. The relative amplitude associated with each phase at ∼50% (47–56% initial phase and 43–53% for the second phase) is consistent with this interpretation. Fig. 1C reveals that observed rates of mantATP binding during the second phase of fluorescence enhancement were also dependent upon the concentration of mantATP but were not linear as observed for the first phase (Fig. 1B). The hyperbolic fit of the data provided the maximum rate of mantATP binding to the second head at 1.6 s⁻¹, therefore implying that mantATP binding to the second head was limited by an event that occurred after mantATP binding to the first head. These results are consistent with an alternating head catalysis model for processive kinesins.

TABLE 1.

Experimentally determined constants for the MT·CENP-E ATPase

MantATP binding	k+1 = 1.4 ± 0.06 μm−1 s−1
	k−1 = 1.6 ± 0.7 s−1
ATP binding (pulse-chase)	K1 = 0.13 ± 0.01 μm−1
	k+1′ = 47.5 ± 0.8 s−1
	K1k+1′ = 6.2 μm−1 s−1
	Kd,ATP = 7.7 μm
	A0 = 1.96 ± 0.1 ADP·Pi per CENP-E site
	Kd,ATP = 16.7 ± 1.7 μm
ATP hydrolysis	k+2 = 24.7 ± 0.5 s−1
	Kd,ATP = 12.3 ± 1.1 μm
	A0 = 1.93 ± 0.1 ADP·Pi per CENP-E site
	Kd,ATP = 44.8 ± 4.4 μm
MT·CENP-E dissociation	k+3 = 1.4 ± 0.01 s−1
	K½,ATP = 6.4 ± 0.5 μm
MT·CENP-E association	k+4 = 0.08 ± 0.004 μm−1 s−1
	k−4 = 0.07 ± 0.01 s−1
	Kd,MTs = 0.9 μm
MantADP release
Head 1	k+5 = 0.9 ± 0.01 s−1
	K½,MTs = 5.1 ± 0.1 μm
Head 2	kmax = 19.4 ± 0.6 s−1
	K½,ATP = 26.6 ± 3.2 μm
MantADP affinity	Kd,Site 1 = 3.6 ± 0.3 nm
	Kd,Site 2 = 31.8 ± 1.4 nm
Steady-state parametersa	kcat = 0.9 ± 0.02 s−1
	Km,ATP = 18.3 ± 2.5 μm
	K½,MTs = 1.5 ± 0.2 μm
MT glidinga	11 ± 0.005 nm/s
MT Plus-end elongationa	1.03 αβ-tubulin subunit/s

^a Data from Sardar et al. (20). Errors reported are S.E.

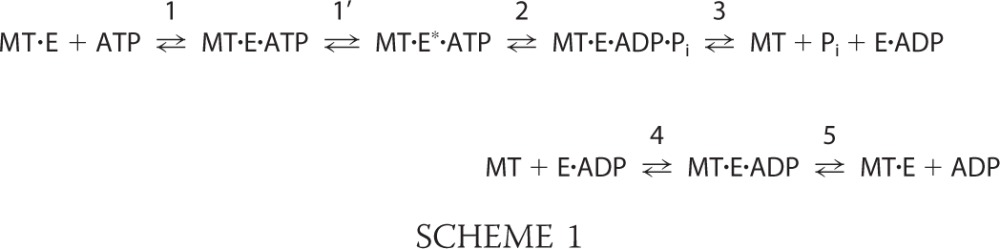
In the second approach, the kinetics of ATP binding were measured using [α-³²P]ATP (Fig. 2). For each of the transients in Fig. 2A, the initial exponential phase corresponds to the first ATP turnover with the linear phase that follows representing subsequent turnovers and corresponding to steady state. The initial observed exponential rates from each transient were plotted as a function of ATP concentration, and the observation that this rate saturates rather than remaining linear is indicative that an ATP-dependent isomerization occurred at the active site to generate the MT·CENP-E*·ATP intermediate that is poised for ATP hydrolysis (Scheme 1, Table 1).

The maximum rate constant of this ATP-promoted conformational change, k₊₁′, is 48 s⁻¹. Another important constant obtained from the transients was the amplitude of the initial exponential phase. The amplitude (A₀) for each transient represents the concentration of ADP·P_i product formed during the first ATP turnover at the CENP-E active site. Fig. 2C presents the amplitude data as a function of increasing ATP concentration. The maximum amplitude at 1.96 ADP·P_i per CENP-E active site (Fig. 2C, Table 1) is consistent with approximately four ATP turnovers by dimeric CENP-E once it associates with the MT. For these experiments, additional salt was included in the [α-³²P]ATP syringe to slow steady-state ATP turnover to better define the exponential burst phase and to obtain a more accurate rate constant for the ATP isomerization step. Although the first ATP turnover is not affected, the degree of processive stepping per encounter with the MT is decreased because of the higher salt concentration (29, 33, 34).

ATP Hydrolysis Is Rapid

To determine the time course of ATP hydrolysis, the acid quench experimental design was used. Fig. 3A presents representative transients of [α-³²P]ADP·P_i product formation, and the data show that there was an increase in both the observed rate and the amplitude of the initial exponential phase as a function of [α-³²P]ATP concentration. The observed rates of the initial exponential phase were plotted as a function of increasing ATP concentration (Fig. 3B), and the fit of the data provided the rate constant of ATP hydrolysis, k₊₂ at 25 s⁻¹ (Scheme 1, Table 1). Fig. 3C presents the pre-steady-state burst amplitude data (A₀) plotted as a function of ATP concentration, yielding A_max of 1.93 μm ADP·P_i per CENP-E active site (Fig. 3C, Table 1). The amplitude results measured here at >1 per active site are consistent with the amplitude results of Fig. 2C and are also indicative of processive ATP hydrolysis.

ATP-triggered ADP Release Is Rapid and Gated

To measure the rate of ADP release during stepping required the generation of an intermediate with the leading head tightly bound to the MT and nucleotide-free with the trailing head detached from the MT with mantADP tightly bound at its active site. This intermediate is also referred to as the “ATP waiting state” in single molecule studies. The nucleotide-free MT·CENP-E complex was preformed (Fig. 4A). MantATP was added at a concentration less than half of that of the active sites of CENP-E. This strategy assumed that mantATP would bind to the trailing head of the dimer (see “Experimental Procedures”) followed by mantATP hydrolysis and phosphate (P_i) release. Because the ADP state for processive kinesins is the most weakly bound MT state, the head with mantADP tightly bound would then detach from the MT to form an intermediate poised for ATP-promoted stepping (Fig. 4A). The MT·CENP-E·mantADP complex was subsequently rapidly mixed in the stopped-flow instrument with ATP, and there was a decrease in the fluorescence as mantADP left the hydrophobic environment of the active site to the aqueous buffer. Note that the buffer control did not show a decrease in fluorescence, consistent with the interpretation that the initial intermediate is long lived, and CENP-E must bind ATP at the leading head for the trailing head to step forward to the next MT binding site followed by mantADP release. The observed rate of mantADP release increased as a function of ATP concentration with the maximum rate constant at 19 s⁻¹ (Fig. 4C, Table 1).

MT·CENP-E Dissociation Is Controlling the Rate of Stepping

To evaluate the kinetics associated with the detachment of CENP-E from the MT, a preformed MT·CENP-E complex was rapidly mixed with ATP, and the turbidity signal was monitored. Fig. 5A presents representative stopped-flow transients at various ATP concentrations. These transients show an ATP concentration-dependent decrease in turbidity as a function of time that is correlated with CENP-E detachment from the MT. The increase in turbidity during the first 100 ms is attributed to the rapid mixing in the stopped-flow instrument rather than a true signal because no ATP concentration dependence was observed for the initial rise in the transients. Fig. 5B shows the observed rates of the MT·CENP-E dissociation kinetics plotted as a function of increasing ATP concentrations. The fit of the data provided the maximum rate constant, k₊₃ at 1.4 s⁻¹ (Fig. 5B and Table 1).

For most kinesins analyzed to date, ATP hydrolysis is required for the kinesin to detach from the MT (36). To test the hypothesis that ATP hydrolysis was required for MT·CENP-E dissociation, the experiment was repeated in the presence of buffer, nucleotides (ADP or ATP), and ATP analogues (slowly hydrolyzable ATPγS or nonhydrolyzable AMPPNP). In the presence of ATPγS or AMPPNP, a slight decrease in turbidity was observed (Fig. 5C). In contrast, the transients for ADP and ATP show a more dramatic decrease in turbidity. These results are consistent with the conclusion that ATP hydrolysis is required for CENP-E detachment from MTs. Because the ADP state is the weakest MT-bound state, we assume that phosphate release occurs first followed by detachment of the CENP-E·ADP head as observed for kinesin-1 and Eg5 (26, 32).

Previously, we measured the rate of MT gliding at 11 nm/s or 1.4 steps/s assuming an 8-nm step; therefore, we propose that MT·CENP-E dissociation coupled with phosphate release is determining the rate of CENP-E processive stepping along the MT lattice. The mantATP binding kinetics (Fig. 1C) revealed that mantATP binding to the second head of the dimer was limited by an event at ∼1.6 s⁻¹. We propose that this limiting event was detachment of the CENP-E·ADP head to complete the first ATP turnover. These results are also consistent with the hypothesis that MT·CENP-E dissociation coupled to phosphate release controls the rate of CENP-E stepping during a processive run.

Productive CENP-E MT Association Is Unusually Slow

Historically, the kinetics of kinesin motor association with the MT were quantified using a turbidity signal because the MT·kinesin complex exhibits a higher turbidity signal than the MT without motors bound or the kinesin motors in solution. However, when these stopped-flow experiments were pursued for CENP-E, the turbidity transients were extremely noisy, and the MT concentration dependence could not be well defined. Because MTs dramatically activate ADP release from kinesin motors, we reasoned that at low MT concentrations, mantADP release would be limited by the productive collision of CENP-E with the MT. Therefore, CENP-E was incubated with a 6-fold higher concentration of mantADP to replace ADP at the active site with mantADP. The CENP-E·mantADP complex was rapidly mixed in the stopped-flow instrument with MTs plus ATP, and the fluorescence signal associated with mantADP release was quantified (Fig. 6). The addition of ATP to the MT syringe diluted the mantADP in solution and mantADP released from the active site after mixing, thereby decreasing the probability of mantADP rebinding to the active site. Representative transients are shown in Fig. 6A. Note that there was no obvious change in the mantADP fluorescence signal in the absence of MTs as shown by the buffer transient, which is consistent with the extremely slow ADP release rate of 0.001 s⁻¹ measured in the absence of MTs (20). In contrast, when the experiment was repeated as a function of MT concentration, there was an increase in the observed rates of mantADP release as a function of increasing MT concentration. At low MT concentrations (0.5–4 μm, Fig. 6B, inset), the observed rates of the initial exponential phase increased linearly as a function of MT concentration. The linear fit of the data provided the second-order rate constant for CENP-E MT association, k₊₄ at 0.08 μm⁻¹ s⁻¹ (Table 1). This rate constant is unusually slow for kinesins. For example, for dimeric kinesin-5 Eg5, it was observed at 2.8 μm⁻¹ s⁻¹ (34, 37), and for kinesin-1, MT association was reported at 10–20 μm⁻¹ s⁻¹ (29, 38, 39). Note too that this slow rate of MT association is not due to weak MT binding by CENP-E. The off rate, k₋₄ at 0.07 s⁻¹, yields an apparent K_d,MT of 0.9 μm.

MantADP Release after MT Collision Is Rate-limiting

To ask whether MT association or ADP release was the rate-limiting step of the pathway, the kinetics of mantADP release were measured at MT concentrations as high as 40 μm (Fig. 6B). The rate constant (k₊₅) for mantADP release upon MT collision was 0.9 s⁻¹. Because the MT-activated steady-state k_cat for CENP-E was reported previously at 0.9 s⁻¹ (20), the mantADP results suggest that MT association of CENP-E coupled with mantADP release limit steady-state ATP turnover in these experiments. However, at conditions where CENP-E is highly processive and exhibits its characteristic long run lengths, we anticipate that it is the 1.4-s⁻¹ stepping rate that will dominate in the steady state because CENP-E MT association would only occur one time per processive run and the rates are similar.

CENP-E Holds ADP Tightly Bound at Both Heads in the Absence of MTs

A series of experiments was pursued to determine the relative affinity of mantADP for CENP-E in the absence of MTs to determine whether CENP-E enters the processive run by a mechanism more similar to dimeric kinesin-1 or Eg5. Nucleotide-free CENP-E at 5 μm was incubated with mantADP at either 5 μm or 2.5 μm and then rapidly mixed in the stopped-flow instrument with 1 mm ATP. Fig. 7A shows that in the absence of MTs, mantADP release from the 5 μm CENP-E/5 μm mantADP complex was biphasic. For the initial exponential phase, the observed rate was 0.086 s⁻¹, and for the second phase, it was 0.004 s⁻¹. When the experiment was repeated with the 5 μm CENP-E/2.5 μm mantADP complex (Fig. 7B), the rates were about the same for each phase with 0.096 s⁻¹ for the initial phase and 0.004 s⁻¹ for the second phase. The amplitudes for both the first and the second phase for the 2.5 μm mantADP experiment were approximately half that observed for the 5 μm mantADP experiment. These results indicate that the 2.5 μm mantADP did not partition to a single high affinity site of the dimer, but rather, both sites of the CENP-E dimer accumulated mantADP, indicative of tight binding of ADP to both sites of the dimer.

To determine the apparent K_d for each site of the dimer, mantADP titration experiments were also pursued (supplemental Materials and Methods, Fig. S1, Table 1). These results estimate the affinity at 3.6 nm for one site and 31.8 nm for the second site of the dimer, consistent with the interpretation that CENP-E holds ADP tightly bound at both active sites of the dimer in the absence of MTs.

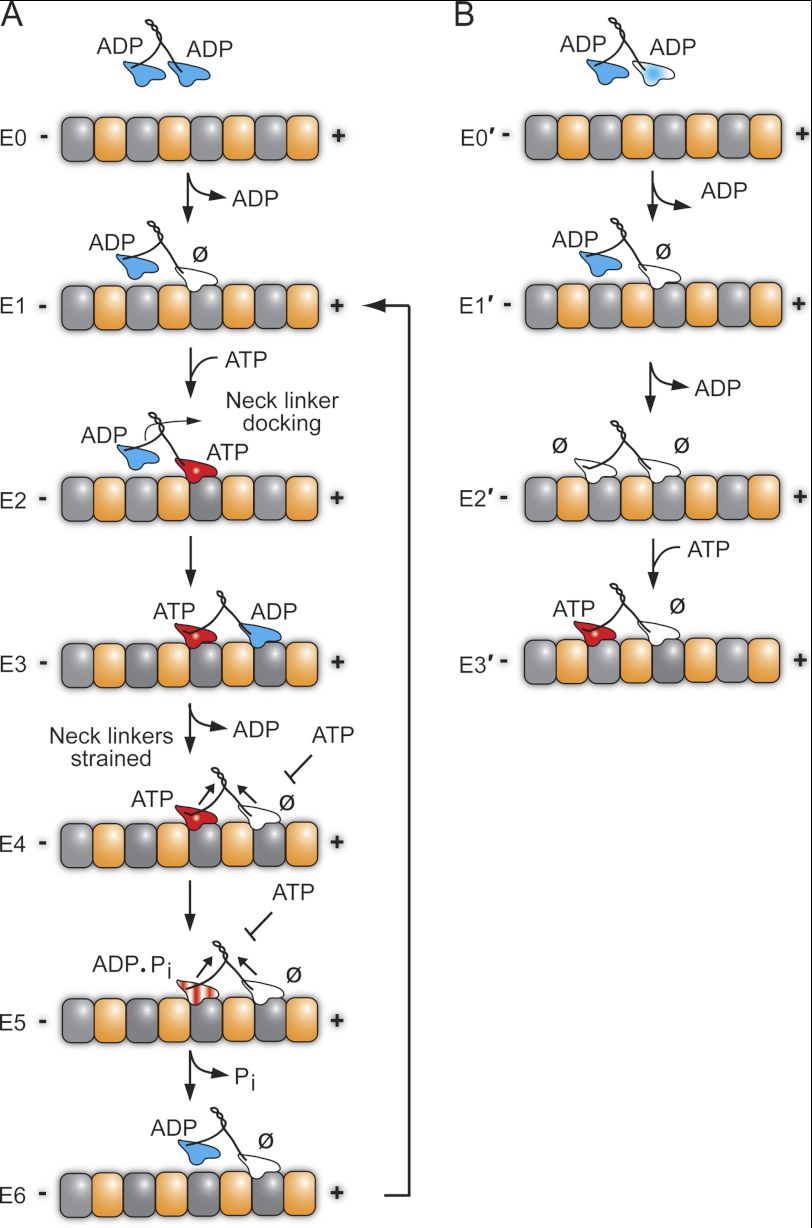
For kinesin-1 in solution, both heads hold ADP tightly bound until the first head collides with the MT followed by rapid ADP release at >200 s⁻¹ (40–43). It is this first step that establishes the asymmetry in the kinesin dimer for the alternating site catalysis mechanism required for hand-over-hand processive stepping. In contrast, Eg5 holds ADP tightly bound at one head and weakly bound at its partner head (Fig. 8B) (26). Krzysiak et al. (26) proposed that the head with ADP weakly bound collides with the MT first, but a structural transition is required, possibly movement of the neck linker, to promote slow binding of the partner head to the MT followed by slow ADP release (Fig. 8B, E0′-E2′) (44–48). The E2′ intermediate has both heads bound to the MT and both heads nucleotide-free. It is from this E2′ intermediate that the processive run begins with ATP binding to the trailing head (Fig. 8B, E3′) (37). The results from Figs. 6 and 7 and supplemental Fig. S1 indicate that CENP-E enters the processive run upon MT collision (Fig. 8A), and therefore, the results exclude a model more similar to Eg5 (Fig. 8B) where the processive run begins from a two-head MT-bound state with both heads nucleotide-free.

FIGURE 8.

Stepping models for CENP-E. A, CENP-E in solution holds ADP tightly bound at each head. The processive run begins upon MT collision to establish the MT plus-end-directed orientation of CENP-E (E1 state) in which the leading head is tightly bound to the MT and nucleotide-free with the trailing head detached with ADP tightly bound. ATP binding at the leading head triggers a series of structural transitions including neck linker docking that advances the ADP-bound head 16 nm forward to the next MT binding site (E2–E3). ADP release is fast, resulting in the E4 two-head-bound state. Strain develops between the two heads such that ATP cannot bind to the leading head (E4). ATP hydrolysis followed by phosphate (P_i) release and detachment of the ADP trailing head relieve the interhead tension (E4–E6). The leading head can now bind ATP, and the cycle is repeated for another 8-nm step coupled to one ATP turnover. B, alternative model for the entry of CENP-E into a processive run. This model proposes that CENP-E enters the processive run from the E2′ state in which both heads are tightly bound to the MT and nucleotide-free as observed for kinesin-5 Eg5. The MT plus (+) and minus (−) ends are indicated with α-tubulin in gold and β-tubulin in gray. ∅, nucleotide-free.

DISCUSSION

This study provides a mechanistic analysis of CENP-E to define the coupling of ATP turnover for the processivity of CENP-E and also its ability to elongate MTs. The results are summarized in Table 1 and incorporated into the model presented in Fig. 8A.

A Model for CENP-E Processive Movement

In solution, CENP-E holds ADP tightly bound at both heads (Fig. 7 and supplemental Fig. S1). The cycle begins as CENP-E collides with the MT, taking the first step (E0–E1), resulting in ADP release at 0.9 s⁻¹ (Fig. 6). The leading head of the E1 intermediate is tightly bound to the MT and nucleotide-free with the trailing head detached from the MT with ADP tightly bound. This first step for CENP-E establishes the asymmetry and MT plus-end directionality required for a hand-over-hand model for CENP-E processive stepping. Note that the ATPase cycles within the dimer are now out-of-phase with each other and must remain coordinated to sustain the long processive runs observed for CENP-E. The results presented show that ATP binding at the leading head is rapid followed by an ATP-promoted isomerization (48 s⁻¹, Figs. 1 and 2), which establishes the intermediate poised for ATP hydrolysis (E1–E4). We propose based on the results of Rosenfeld et al. (22) that the ATP-promoted isomerization correlates with neck linker movement to dock it onto the catalytic core of the leading head and parallel to the MT. This structural transition favors movement of the trailing head forward to the next MT binding site followed by rapid ADP release (19 s⁻¹, Fig. 4) upon MT association (E2–E4). The head-head distance at E4 is ∼8 nm, the distance between MT binding sites. Strain develops between the heads, mediated by the neck linkers, because both heads are tightly bound to the MT. Exit from E4 is proposed to be tightly controlled by interhead tension to prevent premature ATP binding and hydrolysis at the leading head, which would disrupt the coordination and lead to complete motor detachment. Because of the strain, the leading head cannot bind ATP (E4–E5 states). ATP hydrolysis occurs on the trailing head (Fig. 3) followed by phosphate release coupled to detachment of the trailing ADP head (Fig. 5). The E6 intermediate binds another ATP molecule to continue the processive run such that each ATP turnover is tightly coupled to an 8-nm step.

The results indicate that there are two key points in this ATPase cycle that modulate CENP-E interactions with the MT. Because CENP-E-promoted MT gliding occurs at 1.4 steps/s (20), we propose that the detachment of the CENP-E·ADP trailing head at 1.4 s⁻¹ coupled with phosphate release controls the rate of CENP-E stepping during a processive run. We propose that the first step, MT collision coupled with ADP release at 0.9 s⁻¹, is also very slow and limits steady-state ATP turnover at the conditions of these experiments because the MT-activated k_cat is also 0.9 s⁻¹ (Table 1). However, at conditions where CENP-E steps processively for very long distances, the stepping rate at 1.4 s⁻¹ will dominate. This mechanism is also consistent with the proposed model for CENP-E-promoted MT elongation at ∼1 αβ-tubulin/s (Table 1) (20).

CENP-E in Comparison with Conventional Kinesin-1 and Kinesin-5 Eg5

CENP-E shares key characteristics in common with Eg5 and conventional kinesin-1, although these N-terminal motors belong to three different kinesin subfamilies (reviewed in Ref. 36). All three are processive and use an asymmetric hand-over-hand mechanism, thus requiring the coordination of the ATPase cycles to decrease the probability of both heads entering a MT weakly bound state at the same time. The major structural element implicated in the head-head coordination is the neck linker, a sequence of 12–15 amino acid residues that extends from the N-terminal catalytic domain to the α-helical motif that is required for dimerization to form the coiled-coil stalk (49). CENP-E, like kinesin and Eg5, is also gated by interhead tension (E4 state), a regulatory mechanism in which a mechanical and/or chemical requirement must be satisfied for CENP-E to proceed. ATP can only bind to the leading head once the trailing head has detached from the MT (E6 state). In contrast to Eg5, CENP-E and kinesin-1 in solution exhibit tight binding of ADP, and the asymmetry between the heads is established upon MT collision. Furthermore, the tightly controlled coordination of the ATPase cycle at each head is characteristic of both kinesin-1 and CENP-E and responsible for their very long processive run lengths.

Eg5 differs in that it begins its processive run from a two-head bound state in which both heads are nucleotide-free and tightly bound to the MT (Fig. 8B) (26). Another key difference is that ATP hydrolysis is rate-limiting for dimeric Eg5 and slow at 10–12 s⁻¹ (34). These characteristics suggest that for dimeric Eg5, there is a higher probability of both heads reaching the ADP state at the same time, resulting in loss of head-head coordination and leading to the much shorter run lengths observed (18, 26, 34).

What is novel, however, for CENP-E is the exceedingly slow MT association at 0.08 μm⁻¹ s⁻¹ (Fig. 6). This characteristic is very unusual for kinesins in general and Eg5 and kinesin-1 in particular where MT association was observed at 2.8 μm⁻¹ s⁻¹ for dimeric Eg5 and at 10–20 μm⁻¹ s⁻¹ for kinesin-1 (36). Furthermore, slow MT association by CENP-E is not accompanied by a significant off rate (k₋₄ = 0.07 s⁻¹) or weak MT binding (apparent K_d = 0.9 μm). Therefore, even at very high concentrations of MTs, the effective rate for CENP-E MT association cannot be significantly higher than 0.9 s⁻¹ because productive MT association is coupled with ADP release.

CENP-E, Phosphorylation State, and Chromosome Congression

CENP-E during early prometaphase is phosphorylated, and it is at this time that CENP-E establishes unstable lateral and end-on interactions between the kinetochore and MTs (12, 24). Because of the high density of MTs close to the spindle poles, aberrant MT attachments to kinetochores are likely; therefore, the weaker MT binding by phosphorylated CENP-E would enable correction of these inappropriate kinetochore attachments. As chromosomes move toward the equator away from the Aurora kinase gradient, whether through a biorientation mechanism or by CENP-E-mediated lateral chromosome gliding along k-fibers, CENP-E becomes dephosphorylated by protein phosphatase 1 (24). Dephosphorylation of CENP-E results in tighter affinity for MTs and an increase in CENP-E processivity based on increased run lengths observed in vitro. Stable kinetochore attachment and subsequent biorientation does not occur if dephosphorylation of CENP-E is inhibited (24).

Our results interpreted in the context of Kim et al. (24) indicate that the CENP-E slow association step may select for k-fibers and thereby enhance processive movement of chromosomes to the equator through their CENP-E-mediated lateral interactions with the kMTs. After chromosome congression and biorientation to form end-on MT kinetochore attachments, slow MT association may ensure continued stable linkage of CENP-E to kMTs. The kinetics of MT turnover were determined in prometaphase and metaphase with kMTs ∼10-fold slower than turnover of dynamic MTs (t½ = 5–8 min versus ∼40 s (50–52). Therefore, the kinetics of MT turnover are consistent with the hypothesis proposed that slow CENP-E MT association may bias CENP-E binding to kMTs.

In summary, the results presented here indicate that the mechanochemistry of CENP-E does modulate its stepping behavior, and the unique differences observed for CENP-E relative to other processive kinesins may be critical for the functional roles of CENP-E in chromosome congression to avoid chromosome missegregation during anaphase and aneuploidy. In addition, this study also provides additional evidence of how exquisitely tuned each kinesin is for its specific role in cellular transport and/or MT dynamics.