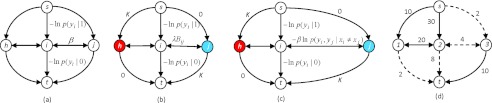
Figure 2.

The edge cost assignment of the graph to solve the minimization of three different energy functions using min s-t cut. A non-negative weight (cost) is assigned to each edge. Min s-t cut is usually solved through a maximum flow algorithm.²² The arrow of an edge shows the direction of the flow. (a) Greig's energy function in Eq. 1 for image binary denoising. (b) Boykov's energy function in which a heuristic boundary term B_ij is defined in Eq. 2 for image segmentation. In addition, seed points for the classes, labeled h for target and j for nontarget, can be indicated by users. For those seed nodes, either a very large number K or zero is assigned to the cost of links to s and t to serve as hard constraints. (c) Our energy function, Eq. 3, derived from CRF, in which the probabilistic boundary term Eq. 5 is defined for image segmentation and is used for cost of edges connecting neighboring voxels. (d) An example of a minimum cut. Dashed lines indicate the edges being cut. The minimum cost of a cut to separate nodes 1, 2, and 3 into two separated groups is 2 + 4 + 8 + 2. After the cut, node 1 and 2 remain connected to s and are classified as target while node 3 remains connected to t and is classified as nontarget.