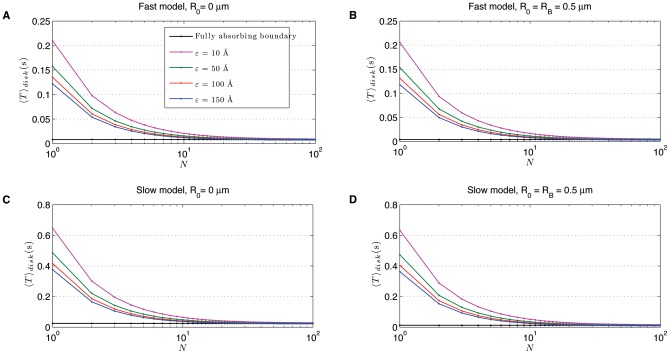
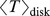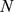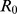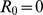Figure 4. Dependence of the GMFPT , expressed in seconds, as function of the number equidistant circular targets on the boundary with two different radius of the initial localization area : the extreme case when and when 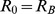, where 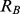is the disk radius.

Panels A and C represent the 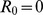case, corresponding to an effector that starts at the origin, whereas panels B and D correspond to an initial particle localization being anywhere inside the bacterium. Each of the panels shows the GMFPT as function of 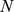for four choices of target radius  = 10, 50, 100 and 150 Å (line colour, see legend in panel A). The black curves represent a limiting case in which the entire boundary of the domain is a target; i.e. 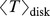becomes the average time required to arrive at the boundary. 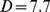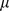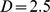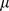In the top row we have considered the ‘fast’ model with m/s, whereas the bottom row displays results for the ‘slow’ model with m/s. 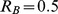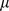In all four panels m.