GABA-mediated spatial and temporal asymmetries that contribute to the directionally selective light responses of starburst amacrine cells in retina

Abstract

Starburst amacrine cells (SACs) are an essential component of the mechanism that generates direction selectivity in the retina. SACs exhibit opposite polarity, directionally selective (DS) light responses, depolarizing to stimuli that move centrifugally away from the cell through the receptive field surround, but hyperpolarizing to stimuli that move centripetally towards the cell through the surround. Recent findings suggest that (1) the intracellular chloride concentration ([Cl⁻]_i) is high in SAC proximal, but low in SAC distal dendritic compartments, so that GABA depolarizes and hyperpolarizes the proximal and distal compartments, respectively, and (2) this [Cl⁻]_i gradient plays an essential role in generating SAC DS light responses. Employing a biophysically realistic, computational model of SACs, which incorporated experimental measurements of SAC electrical properties and GABA and glutamate responses, we further investigated whether and how a [Cl⁻]_i gradient along SAC dendrites produces their DS responses. Our computational analysis suggests that robust DS light responses would be generated in both the SAC soma and distal dendrites if (1) the Cl⁻ equilibrium potential is more positive in the proximal dendrite and more negative in the distal dendrite than the resting membrane potential, so that GABA depolarizes and hyperpolarizes the proximal and distal compartments, respectively, and (2) the GABA-evoked increase in the Cl⁻ conductance lasts longer than the glutamate-evoked increase in cation conductance. The combination of these two specific GABA-associated spatial and temporal asymmetries, in conjunction with symmetric glutamate excitation, may underlie the opposite polarity, DS light responses of SACs.

Key points

• Starburst amacrine cells (SACs), interneurons that are essential to the generation of direction selectivity in the retina, depolarize to light stimuli that move centrifugally away from them, but hyperpolarize to stimuli that move centripetally towards them.

• These directionally selective light responses are dependent on the differential distribution of the Cl⁻ cotransporters NKCC (which mediates GABA-evoked depolarizations by increasing intracellular Cl⁻) and KCC2 (which mediates GABA-evoked hyperpolarizations by decreasing intracellular Cl⁻) on SAC proximal and distal dendrites, respectively.

• We show computationally that directionally selective light responses can be produced in both starburst cell bodies and distal dendrites if (1) there is an intracellular Cl⁻ concentration gradient along SAC dendrites and (2) the response of the dendrites to GABA is relatively long lasting.

• The location of NKCC and KCC2 in different compartments of individual neuronal processes may be an important means by which the brain encodes information.

Introduction

The neural coding of the direction of stimulus motion is a classic example of local neural computation in the nervous system. The vertebrate retina encodes the direction of stimulus motion in that directionally selective (DS) ganglion cells respond well to stimulus motion in one (preferred) direction, but respond little or not at all to motion in the opposite (null) direction (Barlow et al. 1964). Starburst amacrine cells (SACs), interneurons that are presynaptic to the DS ganglion cells and receive glutamate input from non-DS bipolar cells, are an essential component of the mechanism that generates direction selectivity in the retina, because selective deletion of SACs eliminates the direction selectivity of DS ganglion cell light responses (Yoshida et al. 2001; Amthor et al. 2002). Moreover, DS light responses occur first in the retina in SACs (Euler et al. 2002; Gavrikov et al. 2003, 2006; Lee & Zhou, 2006). Specifically, they depolarize to stimuli that move centrifugally through their receptive field (RF) surround, but hyperpolarize to stimuli that move centripetally through their surround (Gavrikov et al. 2003, 2006; Fig. 2D and E).

These robust opposite polarity, DS light responses of SACs, which express Cl⁻ permeable GABA_A receptors (Brandstatter et al. 1995; Zhou & Fain, 1995), and the cation–chloride cotransporters, Na⁺–K⁺–2Cl⁻ (NKCC) and K⁺–Cl⁻ (KCC) (Gavrikov et al. 2006), are dependent on GABA_A receptor activation (Gavrikov et al. 2003, 2006; Lee & Zhou, 2006) and NKCC and KCC activity (Gavrikov et al. 2003, 2006). NKCC and KCC activity, the primary means by which the [Cl⁻]_i is regulated in the central nervous system, determines whether GABA_A receptor activation depolarizes or hyperpolarizes cells (Russell, 2000; Delpire & Mount, 2002; Payne et al. 2003). NKCC transports Cl⁻ into cells so that the Cl⁻ equilibrium potential (E_Cl) is more positive than the resting membrane potential (E_m), resulting in a GABA-evoked depolarization, and KCC extrudes Cl⁻ so that E_Cl is more negative than E_m, resulting in a GABA-evoked hyperpolarization. Recent electrical recordings of starburst somata and immunostaining of starburst dendrites indicate that the differential distribution of the NKCC subtype NKCC2 on the proximal dendrites of SACs and the KCC subtype KCC2 on the distal dendrites mediates the GABA_A-evoked depolarization at the proximal dendrite and GABA_A-evoked hyperpolarization at the distal dendrite, respectively, and the opposite polarity, DS light responses of starburst somata (Gavrikov et al. 2006).

Because SAC distal dendritic tips are the site of synaptic varicosities and calcium-dependent transmitter release (Famiglietti, 1991), it is important to determine whether their DS light responses occur at their distal dendritic tips in addition to their somata. Although imaging of intracellular Ca²⁺ activity suggests that SAC distal dendrites depolarize when a light stimulus moves centrifugally from the soma to the dendritic tip, but not when the stimulus moves centripetally toward the soma (Euler et al. 2002), direct measurements of voltage changes or quantitative measurements of [Cl⁻]_i in these fine dendritic sites are not yet attainable. In addition, it is not known whether a [Cl⁻]_i gradient along SAC dendrites, in conjunction with glutamate excitation from bipolar cells, could contribute to the generation of the DS responses that have been observed at starburst somata (Gavrikov et al. 2006) and the DS responses that may occur at starburst distal dendritic tips. We have therefore examined these possibilities by performing a computational analysis of a biophysically realistic model of a SAC that incorporated previously published experimental data, as well as additional measurements of SAC electrical properties and GABA and glutamate responses that are presented here. Our results strongly suggest that DS light responses can be produced in starburst cell bodies and distal dendritic tips if, in addition to glutamate excitation from bipolar cells, two conditions are both present: (1) there is a [Cl⁻]_i gradient along SAC dendrites and (2) the response of the dendrites to GABA is relatively long-lasting.

Methods

Preparation and electrical recording

Retinal eyecups were obtained following deep general (urethane, induction dose: 2.0 g kg⁻¹, 31% solution, i.p.) and local intraorbital (2% xylocaine) anaesthesia of New Zealand White rabbits (2.5–4.0 kg; Myrtle's Rabbitry, Inc., Thompsons Station, TN, USA). Following enucleations, deeply anaesthetized rabbits were killed by injection of 3.5 m KCl into the heart. Animal care and use complied with UK regulations and The Journal of Physiology policy on animal experimentation, as described in Drummond (2009), and followed all USA guidelines. All procedures involving the care and use of rabbits in this study were reviewed and approved by the Ohio State University Institutional Animal Care and Use Committee (PHS Animal Welfare Assurance No. A3261-01). The superfusate, which was maintained at pH 7.4 and 35°C, contained (in mm): 117.0 NaCl, 30.0 NaHCO₃, 0.5 NaH₂PO₄, 3.1 KCl, 2.0 CaCl₂, 1.2 MgSO₄, 10 glucose and 0.1 l-glutamine.

Following anaesthesia of the rabbits with ketamine (35 mg kg⁻¹, i.m.) and xylazine (5 mg kg⁻¹, i.m.) 1 day before the recording experiments, SACs were selectively labelled by intraocular injection of 0.3 μg 4,6-diamidino-2-phenylindole (DAPI) (Gavrikov et al. 2003, 2006). DAPI-labelled, displaced SACs were identified with brief UV illumination, and then infrared illumination was used for microelectrode manipulation. Biocytin injections confirmed SAC identity. The membrane potential and light-induced responses of displaced SACs were recorded using the patch-clamp technique in the whole-cell configuration, as described previously (Gavrikov et al. 2003, 2006). To measure the input resistance of SACs, short (1 s) pulses of current were sent through the patch electrode. The electrodes had resistances of 6–8 MΩ and contained (in mm): 100.0 potassium gluconate, 14.0 KCl, 4.1 NaHCO₃, 5.0 EGTA, 0.5 CaCl₂, 3.0 MgATP, 0.5 Na₃GTP, 20 sodium phosphocreatine, and 5.0 Hepes. The resting potential and light responses of the cells remained unchanged for at least 30 min under control conditions when this pipette solution was used.

Electrical model

Overall approach

In this paper we computationally investigated the SAC response to a moving bar of light at three specific locations, namely, the SAC body and the two dendritic tips on opposite sides of the cell body. It is important to reconstruct the response in the SAC body because this is the site at which the voltage response to motion has been electrically measured (see Fig. 2; Gavrikov et al. 2006; Lee & Zhou, 2006). The parameters of our computational model were adjusted so that the calculated response in the cell body fit the experimental data (compare Fig. 2D with Figs 4D and 6C).

Figure 2. Responses of displaced SACs to stationary and moving stimuli and to puffs of GABA and glutamate, and the effects of GABA_A receptor blockade on the response to motion.

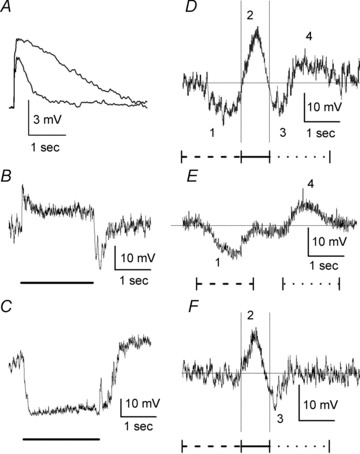
A, GABA and glutamate were puffed from double-barrelled puff pipettes positioned so that the transmitters were applied onto the central portion of the SAC dendritic tree. The concentration of both GABA and glutamate in the pipettes was 0.5 mm, and both GABA and glutamate puffs had the same duration (100 ms). Retinas were treated with bath-applied Co²⁺ (2 mm) before and during the puffs to block synaptic transmission. A constant negative current was injected through the patch-clamp recording electrodes to hyperpolarize the SACs to −60 mV. Representative responses to both GABA (top trace) and glutamate (bottom trace) puffs from a SAC are shown. The puff-evoked voltage changes were filtered at 100 Hz. B, representative light response of a displaced SAC to a stationary spot of light (radius = 150 μm, duration = 2 s). C, representative light response of a displaced SAC to a stationary annulus of light (inner radius = 250 μm, outer radius = 1000 μm, duration = 2 s). D, representative light response of a displaced SAC to a moving bar of light is shown. When the bar of light moved centripetally toward the starburst cell body through the RF surround, the cell generated a slow hyperpolarization (wave 1), followed by a relatively fast depolarization (wave 2) when the bar stimulated the RF centre. As the bar then moved centrifugally away from the cell body and left the RF centre, the SAC initially produced a fast hyperpolarization (wave 3). As the bar then moved centrifugally through the RF surround, the SAC generated a slow depolarization (wave 4). The thin horizontal line through the response record shows the resting membrane potential (–51 mV) of the cell, and the two thin vertical lines through the response record mark the times at which the centre of the moving bar was positioned over the centripetal (left line) and centrifugal (right line) edges of the SAC dendritic tree. The bar moved a distance of 2 mm. Following this movement, the bar remained stationary for 1 s. The record shown began at the start of movement and ended at the termination of the stationary period. E, representative example of the response of a displaced SAC to a moving bar of light that only stimulated the RF surround. The SAC produced a slow hyperpolarization (wave 1) when the bar stimulus moved centripetally through the surround, but did not reach the RF centre (i.e. bar stopped 250 μm from the soma), and produced a slow depolarization (wave 4) when the bar stimulus reversed direction and moved centrifugally over the same distance through the surround. The bar was illuminated and stationary just outside the RF centre during the interval between centripetal and centrifugal motion. The fast depolarization (wave 2 in D) and fast hyperpolarization (wave 3 in D) that are produced by centre stimulation and the termination of centre stimulation, respectively, did not occur. F, light response of a displaced SAC to a moving bar of light in the presence of gabazine. Application of gabazine (100 μm) eliminated the DS light response when the stimulus moved through the surround (waves 1 and 4 in D and E), but did not eliminate the glutamate-mediated, non-DS RF centre light response (waves 2 and 3). B and C, lines under the response records mark the time of light stimulation. D–F, bar dimensions: 500 × 50 μm; speed of movement: 0.5 m s⁻¹. Stimulus markings under the response records: dashed line – centripetal motion through the RF surround; continuous line – motion through the RF centre; dotted line – centrifugal motion through the RF surround.

Figure 4. Effects of an intracellular Cl⁻gradient along the SAC dendrite and a delay in GABA channel closing on the modelled response of a SAC to a moving bar.

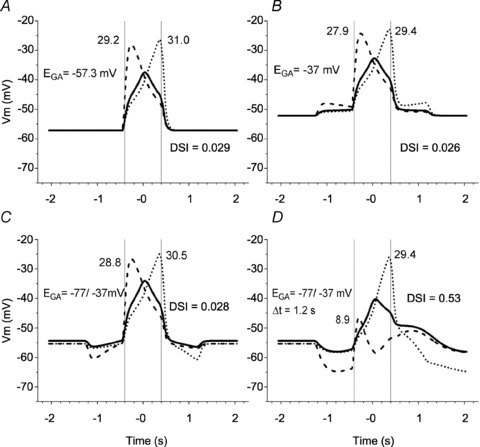
The simulation used both glutamate and GABA inputs to the SAC. The following four conditions were investigated. A, Cl⁻ was distributed passively across the membrane (E_Cl=E_GA=E_m). B, E_GA was constant and more positive than the membrane potential (–37 mV) along the entire dendritic length. C, there was a linear gradient of E_GA along the SAC dendrite (ranging from −37 mV in the body to −77 mV in both dendritic tips). D, the Cl⁻ gradient was as in C, and in addition, the GABA channels stayed open for 1.2 s more after the bar moved away from each segment. In A–D, R_i= 4 MΩ, standard capacitance (τ= 50 ms). Voltage traces, vertical lines and numbers are as in Fig. 3.

Figure 6. Interaction between glutamate and GABA inputs to SAC that produces its DS response.

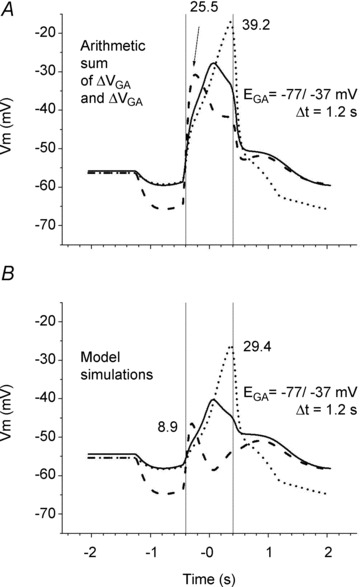
A, the arithmetic sum of the glutamate-evoked (from Fig. 5A) and GABA-evoked (from Fig. 5C) change in voltage. Both the [Cl⁻]_i gradient (from −37 mV in the soma to −77 mV in both dendritic tips) and the delayed closing of the GABA channels (1.2 s) were present. B, the model simulation utilized both the glutamate and GABA inputs to the SAC with the Cl⁻ gradient and the delayed closing of the GABA channels as in Fig. 4D. R_i= 4 MΩ, standard capacitance (τ= 50 ms). Voltage traces, vertical lines and numbers are as in Fig. 3.

However, the responses in the dendritic tips have a greater functional importance than those in the cell body because the synaptic outputs of SACs have been localized to the distal portions of their dendrites (Famiglietti, 1991). SACs produce responses of opposite polarity to centripetal and centrifugal stimulus motion through the RF surround (Fig. 2D and E; Gavrikov et al. 2006), a finding that suggests that the dendritic tips on opposite sides of a SAC would produce different responses, and thus different synaptic outputs, to a stimulus that moved across the SAC RF in one direction. Thus, in addition to adjusting the electrical parameters of our model SAC so that the calculated response to motion in the cell body resembled that actually produced in the cell body, we calculated whether the centripetal and centrifugal dendritic tips on opposite sides of the cell body produced different responses to a stimulus that moved across the RF in one direction. Because SACs are radially symmetrical, this is equivalent to calculating whether one dendritic tip produced different responses to centripetal and centrifugal stimulus motion.

Specifics of the electrical model

The equivalent scheme of an electrical model of a SAC is presented in Fig. 1A. In the model, the dendritic tree of the SAC was divided into four quadrants and converted into a linear cable (Fig. 1B) that could be conveniently analysed. The transmembrane resistances and batteries were grouped into transmembrane elements that represented the K⁺, glutamate and GABA channels of the dendritic tree (Fig. 1A). These transmembrane elements were organized into segments that were each divided by the radial internal resistances (R_i, Fig. 1A). In this respect our circuit is similar to the cable model used by Borg-Graham & Grzywacz (1992). Each segment included three transmembrane (i.e. K⁺, R_K and E_K; glutamate-gated, R_GL and E_GL; and GABA-gated, R_GA and E_GA) elements and represented a specific portion of the SAC dendritic tree that was 2 μm wide. The circuit consisted of 201 segments, each indicated by a number N from 1 to 201, and 201 K⁺, 201 glutamate-gated, and 201 GABA-gated transmembrane elements for a total of 603 transmembrane elements. Segments 1–100 represented the areas of the dendritic tree of the left quadrant of the SAC (QU1 in Fig. 1B) through which the light stimulus moved centripetally toward the soma; the larger the number N of the segment, the closer it was to the centre of the SAC. Segments 102–201 represented the similar areas of the right quadrant of the SAC (QU3) through which the light stimulus moved centrifugally away from the soma; the smaller the number N of the segment, the closer it was to the centre of the SAC. For simplicity, the transmembrane conductance of the SAC dendrites in these quadrants was divided equally between the segments, and the ratio R_K:R_GL:R_GA was the same for all of the segments. The central (101st) segment represented the cell body connected with the two remaining quadrants (QU2 and QU4). Because these two quadrants encompassed the axis that was perpendicular to the direction of stimulus motion, they formally did not participate in motion detection, but still represented half of the SAC dendritic tree. Thus, the central (101st) segment combined all of the K⁺, glutamate-gated and GABA-gated channels of quadrants QU2 and QU4, and consequently had 50% of the total transmembrane conductance of the SAC. As a result, the values of R_K, R_GL and R_GA in the 101st segment were 200 times smaller than those in segments 1–100 and 102–201.

Figure 1. Equivalent electrical circuit of a SAC viewed as a cable (A), its relationship to the dendritic tree of the cell (B), and the projection of the SAC RF onto its dendritic tree with respect to its GABA (C) and glutamate (D) channels.

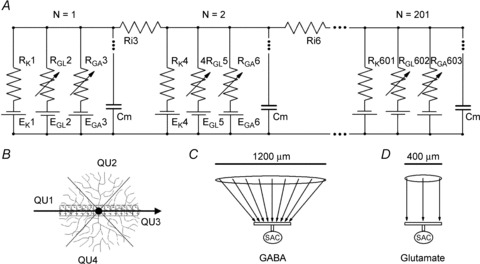
A, although the circuit of a SAC included 201 segments (numbered from 1 to 201), only three segments are shown. In each segment, R_K, R_GL and R_GA were the resistances of the potassium, glutamate-gated, and GABA-gated channels, respectively, and E_K, E_GL and E_GA their respective reversal potentials. R_i was the axial internal resistances of the SAC dendrite cytoplasm, and C_m was the capacitance of the portion of the dendritic tree that corresponded to each segment. B, the arrow shows the direction of movement of the simulated bar of light in a whole-mount view of the SAC. The bar initially moved centripetally toward the soma, first through the RF surround and then through the RF centre, which corresponded to the dendritic tree of the SAC. The bar then moved centrifugally away from the soma, first through the RF centre and then through the surround. Segments 1–100 represented the centripetal quadrant of the SAC dendritic tree (QU1), segments 102–201 represented the centrifugal quadrant of the dendritic tree (QU3), and the central 101st segment combined the two remaining quadrants (QU2 and QU4). C and D, SAC body and dendrites are schematically shown in vertical sections in the lower portions of C and D (perpendicular to the perspective in B). Arrows indicate how the RFs (retinal areas containing photoreceptor cells), which are represented as ovals above the arrows, mapped GABA inputs (C) and glutamate inputs (D) onto the SAC dendrites. GABA inputs mapped the entire RF of the SAC, including both centre and surround, onto the SAC dendritic tree, but glutamate inputs mapped only the RF centre onto the dendrites. See text in Methods for further details of the computational analysis.

Calculations of the cable (numerical approach)

The exact values of the electrical parameters of the circuit were based on our experimental measurements, as described in Results. These experimentally determined electrical parameters, which are shown in Table 1, were used in a series of algebraic equations that implemented Kirchhoff's Law. The resultant calculations determined the transmembrane voltages at every segment of the circuit over time due to changes in the resistors that represented the GABA and glutamate synapses. The calculations consisted of five consecutive steps.

Table 1.

Values for the parameters used in the SAC model

Parameters	Symbol	Value	Conditions
Internal resistance	Ri	0.4 MΩ	Small axial internal resistance (Fig. 3C)
		40 MΩ	Large axial internal resistance (Fig. 3D)
		4 MΩ	All other conditions
Potassium channels equilibrium potential	EK	–95 mV	All conditions
Glutamate channels equilibrium potential	EGL	0 mV	All conditions
GABA channels equilibrium potential	EGA	−57.3 mV	In all segments (Fig. 4A)
		−37 mV	In all segments (Fig. 4B) Figs 4C and D, 5 and 6
		From −37 mV in soma to −77 mV in the most distal dendritic segments
Resistance of potassium channels*	RK	177.6 GΩ	All conditions (dendritic segments)
		888 GΩ	All conditions (soma)
Resistance of glutamate-gated channels*	RGL	266.7 GΩ	In dark (dendritic segments)
		8.0 GΩ	In light (dendritic segments)
		1330 MΩ	In light and dark (soma)
Resistance of GABA-gated channels*	RGA	320 GΩ	In dark (dendritic segments)
		9.6 GΩ	In light (dendritic segments)
		1600 MΩ	In light and dark (soma)
Width of SAC		400 μm	All conditions
Width of dendritic segment		2 μm	All conditions
Width of simulated moving bar of light		54 μm	All conditions
Speed of simulated moving bar of light		500 μm s−1	All conditions

^*Values derived from measurements of the input resistance of starburst amacrine cells in the presence and absence of GABA_A receptor blockade (see text for details).

First, the resistances of the circuit to the left and to the right of each transmembrane element were calculated as follows:

and

where R_tl[i] is the resistance of the circuit to the left of the element with index i, R_tr[i] is the resistance of the circuit to the right of the element with index i, R_i[i] is the radial (axial) internal resistance between the transmembrane elements with indexes i and i+ 1, and R_m[i−1] and R_m[i+1] are the transmembrane resistances next to the left and next to the right, respectively, of the element with index i. Note that the index i refers to each resistor (and to each battery in the equations below) starting from 1 on the very left of the cable and ending with 603 on the very right. Accordingly, if N is an integer that indicates the number of a segment, the transmembrane resistances with indexes i = N× 3 − 2, R_m[1], R_m[4], R_m[7], etc., correspond to R_K1, R_K4, R_K7, etc., respectively, the transmembrane resistances with indexes i = N× 3 − 1, R_m[2], R_m[5], R_m[8], etc., correspond to R_GL2, R_GL5, R_GL8, etc., respectively, and the transmembrane resistances with indexes i = N× 3, R_m[3], R_m[6], R_m[9], etc., correspond to R_GA3, R_GA6, R_GA9, etc., respectively (see Fig. 1A). Also, only R_i[i] with indexes i = N × 3 were different from 0 (and only these are shown in Fig. 1A), guaranteeing that the transmembrane potentials were the same within each segment, regardless of whether the potassium, glutamate-gated or GABA-gated element was measured. However, the transmembrane potentials can be different in different segments.

Second, the total resistance of the circuit for each battery, R_tot[i], was calculated as follows:

Third, the voltage that each battery generated on its own transmembrane element, V_mf[i], was calculated as follows:

where E_m[i] is a battery of transmembrane element with index i. Again, as shown in Fig. 1A, the batteries with indexes i = N × 3 − 2 correspond to E_Ki, the batteries with indexes i = N × 3 − 1 correspond to E_GLi, and the batteries with indexes i = N × 3 correspond to E_GAi.

Then, in the fourth step, the voltages that each battery generated across all other transmembrane resistances, except its own, V_mf[i,j], were calculated as follows:

for j > i (i.e. to the right from the battery with index i) and V_mf[i,j]=V_mf[i] when j= i,

for j < i (i.e. to the left from the battery with index i) and V_mf[i,j]=V_mf[i] when j=i. These calculations produced a two-dimensional set of data that defined the voltages generated by all of the batteries (first index, i) across all of the transmembrane resistors (second index, j).

In the fifth and last step, the voltages resulting from all of the batteries in the circuit in each transmembrane element were summed as follows: 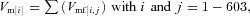giving us the transmembrane potentials across each transmembrane element. As has been mentioned, the transmembrane potentials are equal to each other within each segment (i.e. V_{m[N×3 − 2]}=V_{m[N×3 − 1]}=V_m[N×3]). Accordingly, the transmembrane potentials were calculated in each of the 201 segments of the cable.

Simulation of light stimulus motion

Light stimulation was simulated by decreasing R_GL (i.e. by increasing the glutamate-gated cation conductance) and R_GA (i.e. by increasing the GABA-gated Cl⁻ conductance), each by a factor of 0.03 (see Table 1). Thus, in our computational analysis both R_GL and R_GA were always in one of two states, a high resting value that simulated darkness and a low value that simulated light stimulation. To simulate motion (always from left to right in this study), R_GL and R_GA were sequentially decreased starting with the 1st segment on the left end of the cable and ending with the 201st segment on the right end. R_GL and R_GA in each segment stayed low while the light was located in the RF area that projected onto that segment. (Note: the RF for R_GL is different from the RF for R_GA, as discussed below.) When the light moved away, R_GL immediately returned to the high resting value. This was not always the case for the GABA-gated channels. In some simulations (i.e. in Figs 4A–C and 5B), R_GA returned from its low light value to its high resting value immediately after the light moved away from the location, but in other simulations (i.e. in Figs 4D, 5C and 6B), it returned to its high resting value after a 0.2–1.2 s delay.

Figure 5. Comparison of voltage changes in SAC soma and dendrites in response to a moving bar calculated separately for glutamate channels (A) and GABA channels (B and C).

A, the simulation used only glutamate inputs to the SAC, the same conditions as in Fig. 3B. B, the simulation used only GABA inputs to the SAC; there was a linear gradient of E_GA along the SAC dendrite (ranging from −37 mV in the body to −77 mV in both dendritic tips). The GABA channels closed as soon as the bar moved away from each segment. C, the simulation used only GABA inputs to the SAC; the Cl⁻ gradient was as in B, and in addition, the GABA channels stayed open for 1.2 s more after the bar moved away from each segment. R_i= 4 MΩ, standard capacitance (τ= 50 ms). Voltage traces, and vertical lines are as in Fig. 3. Note that the range for voltage changes in B and C is different from that in A.

Our model simulated the glutamate-mediated depolarization of SACs that occurs when light stimulates the SAC RF centre (wave 2 in Fig. 2D and F), but did not simulate the glutamate-mediated hyperpolarization that occurs at the termination of RF centre stimulation (wave 3 in Fig. 2D and F). A third state of R_GL, which is higher than that at rest, would have had to be added to generate this hyperpolarizing off-centre response. Because this off-centre response is non-DS (Gavrikov et al. 2006), we chose not to implement this response property to avoid an unnecessary complication.

The width of the simulated bar of light was 54 μm, which is similar to the width of the moving bar used in our electrical recording experiments. Accordingly, the light could simultaneously decrease R_GL and R_GA in up to 27 2-μm-wide contiguous segments of the modelled SAC. Since the speed of the simulated bar's movement across the SAC RF was 0.5 mm s⁻¹ (see Table 1), as in most of our electrophysiological experiments, 4 ms was required to shift from one segment to another (the distance of 2 μm) and decrease R_GL in the next segment (in the case of R_GA, a three times longer time is required, see explanation below). Accordingly, we used 4 ms as a time step in the model, that is the membrane potential of the SAC cable associated with changes in the transmembrane resistances was recalculated every 4 ms.

The calculated values of the local membrane potentials were then corrected to take into account the influence of membrane capacitance as follows:

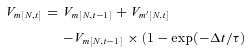where V_m[N,t] is the membrane potential in segment N at time t corrected for capacitance, V_m′[N,t] is the membrane potential in segment N at time t, calculated with no capacitance present, V_m[N,t−1] is the membrane potential in segment N at one time interval earlier, Δt is the time interval (= 4 ms), and τ is the RC time constant that was 50 ms in all of our calculations, except that in Fig. 3A.

Figure 3. Influence of the capacitance and axial internal resistances on modelled response of SAC to moving bar.

The simulation used only glutamate inputs to the (‘gabazine treated’) SAC. The following four conditions were investigated. A, R_i= 4 MΩ, no capacitance (τ= 0); B, R_i= 4 MΩ, standard capacitance (τ= 50 ms); C, R_i= 0.4 MΩ (small axial internal resistances), standard capacitance (τ= 50 ms); D, R_i= 40 MΩ (large axial internal resistances), standard capacitance (τ= 50 ms). Here and in Figs 4–6, the thick continuous line denotes the membrane potential calculated in the cell body (101st segment), the dashed line denotes the membrane potential calculated in the centripetal dendritic tip (1st segment), and the dotted line denotes the membrane potential calculated in the centrifugal dendritic tip (201st segment). The thin vertical lines mark the time that the centre of the moving bar was positioned at the centripetal (left line) and centrifugal (right line) edges of the SAC dendritic tree, as shown in Fig. 2A. The maximum response amplitudes (in mV) in the dendritic tips are shown near the corresponding traces. The resultant DSIs (see Results for definition) for each of the four conditions are also shown.

Although the diameter of the SAC dendritic tree in the portion of the rabbit retina in which our electrical recordings were obtained (approximately 1–2 mm from the visual streak) did not exceed 350–400 μm, its RF is much broader due to the presence of its RF surround. When moving stimuli were used, the SAC RF was approximately 3 times larger in diameter than its dendritic tree (Gavrikov et al. 2006). Since in the model the diameter of the SAC dendritic tree was 400 μm (2 μm × 200 segments), the diameter of its RF was 1200 μm. Experimental results have indicated that the RF surround projection onto the SAC dendritic tree is mediated by GABA, because peripheral responses can be blocked by the specific GABA_A receptor antagonist gabazine (Gavrikov et al. 2006; Lee & Zhou, 2006). We thus assumed that in the case of GABA-driven inputs, the entire SAC RF converges onto the 3 times smaller SAC dendritic tree (Fig. 1C). The laterally oriented dendrites of amacrine cells, including other SACs, are likely to provide the GABA input (Famiglietti, 1991; Lee & Zhou, 2006). It should be noted that Lee & Zhou (2006) found that the GABA-driven RF surround was ∼2 times larger in diameter than the SAC dendritic tree. The finding that SACs use GABA to communicate with neighbouring SACs through the very tips of their dendrites (Lee & Zhou, 2006) suggests that the size of the SAC RF is ∼3 times larger than its dendritic tree (RF diameter = diameter of postsynaptic SAC + diameters of two presynaptic SACs on opposite sides of the postsynaptic cell), although the contribution of the outermost portion of the RF surround may be relatively small. In addition, glutamate-gated synapses are also distributed throughout the entire SAC dendritic tree, but because they are postsynaptic to vertically oriented bipolar cells, glutamate-driven inputs in the model were activated only when the central part of the SAC RF, which was equal in size to the dendritic tree, was stimulated (Fig. 1D).

The difference between the projections of GABA and glutamate inputs onto the SAC dendritic tree has important consequences concerning the timing of these two inputs. Because light stimulation of any portion of the SAC RF (diameter = 1200 μm) provides GABA input, but stimulation of only the RF centre (diameter = 400 μm) provides glutamate input, a light stimulus moving across the RF will affect the GABA conductance 3 times longer than the glutamate conductance by starting earlier and finishing later. Accordingly, the projection of a light stimulus onto the cable moves 3 times slower for GABA inputs than for glutamate inputs. In addition, light stimulation of a portion of the SAC RF will lead to activation of GABA and glutamate channels that are located in most cases in different segments of the SAC dendritic cable. For example, when the light bar moving from the periphery reaches the SAC RF centre (200 μm from the cell body), its leading edge will decrease R_GL at the very left of the cable (1st segment), but decrease R_GA in the portion of the cable much closer to its centre (67th segment).

The described difference between the projections of GABA and glutamate inputs onto the SAC dendritic tree is one of the special features of our model that makes it dissimilar to other cable models, such as the Borg-Graham & Grzywacz (1992) model. Another special feature of our model is the numerical approach, which is described above, that was used to calculate the potentials in the cable. A custom-made computer program was implemented to perform these calculations.

Results

Electrophysiology results that form the basis of the SAC cable model

SACs receive both glutamate and GABA-mediated synaptic inputs (Brandstatter et al. 1995; Taylor & Wassle, 1995; Zhou & Fain, 1995). We compared the glutamate and GABA evoked responses of displaced SACs when synaptic transmission was blocked by puffing glutamate and GABA onto SACs in retinas treated with Co²⁺. For better comparison of the responses, both glutamate and GABA were puffed from double-barrelled micropipettes onto the same SAC at the same dendritic location using puffs of the same duration (100 ms) and neurotransmitter concentration (0.5 mm). As shown in Fig. 2A, SAC responses to GABA puffs lasted significantly longer than responses to glutamate puffs. In all cases (n = 5) in which responses to glutamate and GABA were obtained from the same SAC, the half-time decay of the GABA responses was more than 1 s longer than that of the glutamate responses. This difference in the duration of the GABA and glutamate responses of SACs can probably be attributed to the slower clearance of GABA, compared to glutamate, from the extracellular space by their respective transmembrane transporters and/or to the higher GABA affinity and reduced desensitization of the δ subunit-containing GABA_A receptors (Semyanov et al. 2004; Glykys & Mody, 2007), which are located on SAC dendrites (Brandstatter et al. 1995), compared to the glutamate affinity and rate of desensitization of the glutamate receptors expressed by SACs.

Displaced SACs have a classical On-centre and Off-surround RF organization with glutamate-mediated excitatory input from the RF centre and GABA mediated inhibitory input from the surround (Taylor & Wassle, 1995; Peters & Masland, 1996; Gavrikov et al. 2006; Lee & Zhou, 2006). When the excitatory centre of the SAC RF, which corresponds approximately to the dendritic tree of the cell, was stimulated with a centred stationary spot of light, the cells responded with a sustained depolarization (Fig. 2B), but when a stationary light stimulated the RF surround, SACs responded with a hyperpolarization (Fig. 2C). It should be noted that the SAC central and surround responses behaved differently at light offset. The central glutamate-mediated response ended at light offset, showing a strong hyperpolarizing undershoot. In contrast, the GABA-mediated SAC response to stimulation of the RF surround slowly returned to baseline keeping the cell hyperpolarized for another half-second after light offset.

When a light stimulus moves across the retina, a non-DS retinal neuron with an On-centre and Off-surround RF organization will produce a prominent depolarization when the stimulus moves through its RF centre and produce hyperpolarizations before and following the depolarization when the stimulus moves through its RF surround. But the response of a displaced SAC to a moving stimulus did not exhibit this pattern; rather it was directionally selective. As shown in Fig. 2D for a typical displaced SAC, which was recorded with a patch electrode in the whole-cell configuration, and as reported previously using both patch-clamp whole-cell and fine-tipped intracellular microelectrode recording (Gavrikov et al. 2006), when the bar of light moved centripetally toward the cell body through the RF surround, the SAC generated a slow hyperpolarization (wave 1 in Fig. 2D), but responded with a slow depolarizing wave (wave 4 in Fig. 2D) as the bar moved centrifugally away from the cell body through the RF surround. A relatively fast depolarization (wave 2 in Fig. 2D) to stimulation of the RF centre, followed by a fast hyperpolarization (wave 3 in Fig. 2D) when RF centre stimulation ended, occurred between these two surround responses. As shown in Fig. 2E, the fast depolarization and subsequent fast hyperpolarization were not generated if the moving bar did not stimulate the RF centre. Rather, the SAC produced a slow hyperpolarization (wave 1) to a slit stimulus that moved centripetally through the surround but did not reach the RF centre, and produced a slow depolarization (wave 4) when the slit stimulus reversed direction and moved centrifugally through the surround. The slow hyperpolarization and slow depolarization to stimulus motion through the surround in the centripetal and centrifugal directions, respectively, represent the opposite polarity DS light response of SACs, whereas the fast depolarization and subsequent fast hyperpolarization represent the non-DS component of the SAC response to stimulus motion. As shown previously (Gavrikov et al. 2006), the fast depolarization is produced by centre stimulation. Moreover, because the subsequent fast hyperpolarization only occurs when centre stimulation is removed (Gavrikov et al. 2006) and does not occur when only the RF surround is stimulated (Fig. 2E), it is likely to be mediated by termination of the RF centre mechanism, and not by the RF surround mechanism. As noted above (see Methods, Simulation of light stimulus motion) and as shown previously (Gavrikov et al. 2006; Lee & Zhou, 2006), the diameter of the SAC RF surround, which evokes the DS light response when stimulated by moving objects, is ∼3-fold larger than the diameter of the RF centre (i.e. RF surround diameter = diameter of 3 adjacent SACs). Although not investigated or modelled in the current study, displaced SACs also exhibit an additional, more peripheral RF surround, which evokes a transient hyperpolarization of SACs when stimulated by stationary stimuli (see Fig. 1 in Gavrikov et al. 2006), possibly by inhibiting glutamate input from bipolar cells to SACs (Lee & Zhou, 2006).

Figure 2F shows that the DS component of the SAC response to stimulus motion through the surround is GABA mediated. Specifically, the slow hyperpolarization to centripetal stimulus motion through the RF surround (wave 1 in Fig. 2D and E) and the slow depolarization to centrifugal stimulus motion through the surround (wave 4 in Fig. 2D and E) were both blocked by application of gabazine, a selective GABA_A receptor antagonist. In contrast, the non-DS component of the SAC response to stimulus motion through the RF centre (i.e. waves 2 and 3) was not blocked by application of gabazine, indicating that the fast depolarization and the subsequent fast hyperpolarization were not produced by GABA input and were likely to have been produced by glutamate input from bipolar cells in the RF centre (Gavrikov et al. 2006). As described below, gabazine also hyperpolarized SACs and increased their input resistance.

One of the aims of this computational study was to reconstruct a similar response to a moving stimulus, as that recorded experimentally in the SAC body using whole-cell patch-clamp (see Fig. 2D) and sharp-tipped intracellular electrodes (Gavrikov et al. 2006), and to determine the electrical conditions that produce it. As described above (see Methods, Simulation of light stimulus motion), the fast non-DS hyperpolarization that results from termination of RF centre stimulation (wave 3 in Fig. 2D and F) was not included in the model for the sake of simplicity.

Computation of SAC light responses with GABA channels blocked

We used an electrical cable model (see Methods, Fig. 1) to calculate the responses of SACs to moving bar stimuli. The values of the electrical elements of the circuit in Fig. 1A were determined based on measurements of the input resistance and resting membrane potential of SACs, while we assumed for simplicity that the input resistance was equal to the total transmembrane resistance of the cell. Our strategy was to determine whether the DS light responses of SACs are dependent on glutamate and GABA input by first computing the SAC response with only glutamate input and then computing the SAC response with both glutamate and GABA channels functioning. Thus, as a first step, we calculated a variant of the model that included only potassium channels and glutamate-gated channels, but not GABA-gated channels, which corresponds to the experimental condition in which GABA_A channels are blocked by the selective GABA_A receptor antagonist gabazine. The input resistance of SACs with GABA_A channels blocked was 268.2 ± 39.3 MΩ (mean ± SEM, n = 8) and the membrane potential was −57.9 ± 3.5 mV (n = 8). Therefore, because the potassium equilibrium potential in our experimental conditions and, consequently, all E_K in the circuit were equal to −95.4 mV, and the glutamate channel reversal potential (all E_GL in the circuit) was equal to 0 mV, one can conclude that the ratio between the K⁺ and the glutamate-gated channel conductances in the resting state was approximately 3:2. In order to match the transmembrane resistance of the modelled cell to the experimentally measured input resistance, we defined all R_K (except R_K101 in the ‘cell body’) = 177.6 GΩ, and all R_GL (except R_GL101) = 266.6 GΩ. In the ‘cell body’R_K101 = 888 MΩ and R_GL101 = 1333 MΩ. With these values for the resistors and batteries of the potassium and glutamate-gated channels, the total transmembrane resistance (≍ input resistance) of our simplified ‘gabazine-treated’ SAC model was equal to 266.5 MΩ, and the membrane potential (E_m) of the SAC was equal to −57.3 mV, values that are close to the results of our experimental measurements.

Light stimulation was mimicked by decreasing R_GL by a factor of 0.03, which corresponded to increasing the cation conductance by ∼110 pS (or about one glutamate-gated synapse) per segment. This light-induced increase in glutamate conductance was very close to, although a little smaller than, the value used in the computational modelling of the SAC dendritic tree by Smith and coauthors (Tukker et al. 2004). Although voltage changes in each segment of the cable were calculated, the results of calculations in only three particularly important segments are presented. These segments are the cable centre (‘cell body’, segment 101) and the leftmost and rightmost ends (segments 1 and 201, respectively). Comparison of simulated responses in the centre of the modelled SAC with the experimental records obtained from starburst cell bodies enabled us to adjust the electrical parameters of the model to achieve a similarity between the computational results and the patch-clamp recordings. Determination of the voltage changes at both ends of the cable (i.e. the two ‘dendritic tips’) was one of the principal aims of this work, because the Ca²⁺-dependent synaptic outputs of SACs onto DS ganglion cells are located at SAC distal dendrites (Famiglietti, 1991).

The results of the simulation are presented in Fig. 3. The response in the SAC body calculated for the condition in which GABA channels were blocked was similar in time course and amplitude to the experimentally measured light responses of SAC under gabazine treatment (Gavrikov et al. 2006). Movement of the light bar through the peripheral 400 μm of the RF surround had no effect on the SAC membrane potential (Fig. 3). When the leading edge of the moving bar reached the RF centre at the edge of the SAC dendritic tree, the whole dendritic tree of the SAC began to depolarize. The responses in the cell body and dendritic tips exhibited dynamic differences. The depolarization in the centripetal tip (i.e. the tip of the dendrite in quadrant 1 in Fig. 1B through which the bar moved centripetally toward the body; dashed line in Fig. 3) rose faster than the depolarizations in the body (continuous line in Fig. 3) and the centrifugal tip (i.e. the tip of dendrite in quadrant 3 in Fig. 1B through which the bar moved centrifugally from the body; dotted line in Fig. 3), because the stimulus initially opened ‘glutamate channels’ in the centripetal tip itself and its contiguous areas. The depolarization in the centripetal tip reached a maximum when the entire bar was positioned in the RF centre with the trailing edge of the bar located at the centripetal tip. As the bar then moved farther to the right and opened ‘glutamate channels’ in other parts of the SAC dendritic tree, the depolarization in the centripetal tip declined. The response in the cell body reached its maximum when the middle of the bar was positioned at the very centre of the RF and the dendritic tree, and the response in the centrifugal tip was maximal when the leading edge of the bar arrived at the rightmost side of the RF centre.

When the membrane capacitance was not included (Fig. 3A), the calculated response in the centrifugal dendritic tip (dotted line) was the mirror image of the response in the centripetal tip (dashed line) and both responses had precisely the same maximal amplitude. The response calculated in the cell body (continuous line) was perfectly symmetrical relative to time 0, which was defined as the time when the middle of the moving bar was positioned exactly at the SAC body (i.e. the very centre of the RF).

The responses were not symmetrical and were slightly different in amplitude when the membrane capacitance, which is always present in biological membranes, was included in the analysis. In all our calculations (except those used in Fig. 3A), we assumed the presence of a membrane capacitance that together with a transmembrane resistor produced an RC filter with a time constant, τ, of 50 ms, a value that is typical for a neuronal membrane with specific membrane resistivity of 50 kΩ cm² and specific capacitance of 1 μF cm⁻². Because of the presence of the RC filter, the electrical responses developed more slowly and were shifted to the right on the time axis (Fig. 3B). The capacitance also reduced the amplitude of the voltage changes and this reduction was larger for faster changes. As a result, the faster rising centripetal response had a slightly smaller amplitude (33.2 mV) than the more slowly rising centrifugal response (34.9 mV).

The response amplitudes at the centripetal and centrifugal dendritic tips were thus different. This directional difference can be quantitatively characterized with the direction selectivity index (DSI), which in the case of SAC responses can be calculated as follows:

where V_cpt is the maximum voltage change in the centripetal dendritic tip and V_cfg is the maximum voltage change in the centrifugal dendritic tip on the opposite side of the SAC dendritic tree. Because of the effect of capacitance, V_cpt was slightly smaller than V_cfg, and as a result, DSI = 0.026.

As we have noted, the calculated responses in the dendritic tips were different from the response in the cell body. The extent of the differences in amplitude and dynamics of the responses in the dendritic tips and body depended on the axial internal resistances of the cytoplasm in the dendrites (R_i, Fig. 1A), which determines how well different portions of the dendritic tree are electrically connected with each other and the cell body. In all our calculations (except for those in Fig. 3C and D), we used R_i= 4 MΩ, which corresponded to the axial internal resistances of a fragment of dendrite with section area of 1 μm², length of 2 μm, and typical cytoplasmic resistivity of 200 Ω cm. With the chosen values for R_K, R_GL and R_i, the theoretical space constant λ (i.e. the distance at which a passively propagated voltage decreases by a factor of e) = 326 μm. This value for the space constant represents a modest electrical connection between the parts of each SAC, and seems reasonable. For comparison, Smith and coauthors used λ≍ 400 μm (i.e. a little stronger, but practically similar electrical connection) in modelling the SAC dendritic tree (Tukker et al. 2004). The larger the R_i, the larger the difference between responses in the tips and body (Fig. 3C and D), as shown previously (Velte & Miller, 1997). Variations in R_i also had a small effect on direction selectivity, and both electrical isolation of the dendrites from the body (when R_i was larger) and an improved electrical connection of the SAC compartments (when R_i was smaller) reduced DSI.

Computation of GABA influence on SAC light responses

Role of spatial asymmetry in [Cl⁻]_i

Previous experimental data have suggested that the spatial asymmetry (differential distribution) in intracellular Cl⁻ along SAC dendrites underlies in part the generation of direction selectivity in the retina (Gavrikov et al. 2003, 2006). Because the [Cl⁻]_i determines the amplitude and polarity of GABA-evoked responses, we performed a series of calculations to examine the role of GABA channels in shaping the SAC response. It should be noted that another anion, HCO₃⁻, which is present in significant concentrations on both sides of the neuronal membrane, can also flow through ionotropic GABA channels. However, the contribution of HCO₃⁻ to GABA-mediated postsynaptic potentials (PSPs) is small when [Cl⁻]_i is relatively high (10–15 mm, Farrant & Kaila, 2007), as it is in our experimental and computational conditions. Thus, we assume that E_GA=E_Cl in all our calculations.

The experimentally measured input resistance of SACs in control conditions (without gabazine) was 201.3 ± 14.9 MΩ (n = 13), which is about three-quarters of the input resistance measured when GABA channels were blocked, indicating that the GABA channels are responsible for approximately one-fourth of the total transmembrane conductance of the cells in resting conditions. Consequently, we defined all R_GA (except in the 101st segment)as equal to 320 GΩ, and R_GA101 (‘cell body’) as equal to 1600 MΩ. After adding together R_GA with previously defined R_K and R_GL, the total transmembrane resistance of the modelled SAC was 200 MΩ. Also, because the addition of GABA channels reduced by a small amount the total transmembrane resistance of the SAC, the space constant decreased to 283 μm.

Figure 4 shows the effects of GABA on the SAC responses to a moving bar both with and without cation–Cl⁻ cotransporter activity and when GABA-evoked responses were either brief or lasted longer. Figure 4A depicts the SAC response to a moving bar of light when there was no cation–Cl⁻ cotransporter activity, such as occurs when the cotransporters are blocked by bumetanide and furosemide, and Cl⁻ was distributed passively across the SAC plasma membrane. In this condition, the E_GA (=E_Cl in the model) should be equal to the SAC membrane potential determined by K⁺ and glutamate-gated channels, i.e. −57.3 mV. The response in the SAC body calculated for the condition in which NKCC and KCC were blocked was similar in dynamics and amplitude to the experimentally measured responses of SACs treated with bumetanide and furosemide (Gavrikov et al. 2006). These simulated responses were also similar to those illustrated in Fig. 3B, because in both cases no voltage changes occurred when the bar moved through the SAC RF surround. Stimulation of the surround did lead to opening of the GABA channels, but it did not generate currents and voltage changes, because the Cl⁻ equilibrium potential was equal to the SAC membrane potential. The only effect that GABA channel opening had in this condition was a shunting of the SAC membrane and a reduction in the amplitude of glutamate-induced responses, which developed when the bar reached the SAC RF centre. Thus, addition of GABA channels in this simulation had very little effect on the DSI.

In fact, as experimental data have shown (Gavrikov et al. 2006), Cl⁻ does not distribute passively across SAC membranes. The average resting membrane potential of SACs before treatment with gabazine was 5.6 mV more positive (–52.3 ± 3.6 mV, n = 13) than the average SAC membrane potential after gabazine application. To mimic this tonic depolarizing effect of endogenous GABA on the SAC, we assumed that E_GA was equal to −37 mV through the whole length of the cable; this shifted the resting membrane potential of the modelled SAC to −52.2 mV. In the simulations presented in Fig. 4B, the moving bar opened GABA channels and depolarized the SAC because E_GA was more positive than the membrane potential of the cell. The DSI, however, was low (= 0.026).

Although previous experimental data have demonstrated that endogenous GABA has a depolarizing effect on the SAC resting membrane potential, it has also been shown that stimulation of the RF surround produces a GABA-mediated hyperpolarization of SACs (Gavrikov et al. 2006), a finding that suggests that E_GA in the distal part of the SAC dendritic tree is more negative than the membrane potential. We therefore assumed for the next simulation that E_GA was more positive than E_m in the centre of the SAC dendritic tree, becoming more and more negative towards the distal ends of the dendrites, i.e. there was an [Cl⁻]_i gradient along the SAC dendrite. The molecular basis for such a Cl⁻ gradient is the demonstrated differential distribution of KCC2 and NKCC2 in the distal and proximal portions, respectively, of SAC dendrites (Gavrikov et al. 2006). To implement this state, E_GA in the centre (101st) element was still set to −37 mV, but became progressively more negative by −0.4 mV in each segment as one moved toward both ends of the cable, so that E_GA in both dendritic tips was equal to −77 mV. Under these conditions, simulated light stimulation of the SAC receptive field surround produced a GABA-mediated hyperpolarizing response when the bar moved centripetally (Fig. 4C, between −1.2 and −0.4 s), which was similar to the experimentally recorded voltage response of the SAC body (wave 1 in Fig. 2D). However the calculated voltage changes in the cell body did not exhibit a slow depolarizing wave when the bar moved centrifugally through the RF surround (Fig. 4C, between 0.4 and 1.2 s), as has been observed experimentally (wave 4 in Fig. 2D). The SAC response in the cell body was still almost symmetrical and the responses in the dendritic tips were still nearly mirror images (DSI = 0.028). In addition, SAC direction selectivity was not noticeably improved if a maximum hyperpolarizing effect of GABA, in which E_GA=−97 mV in all segments of the model, was tested (DSI = 0.032, data not shown).

Role of long-lasting GABA responses

In addition to experimental observations consistent with an intracellular Cl⁻ gradient along SAC dendrites (Gavrikov et al. 2006), our experimental data suggest that the GABA-mediated responses of SACs may last longer than the glutamate-mediated responses (see Fig. 2A; also compare Fig. 2B and C). But in all our previous simulations, both GABA and glutamate channels opened at the moment that the leading edge of the moving bar was projected onto the corresponding part of the RF (see Fig. 1C and D) and closed at the moment that the trailing edge of the bar moved from that RF location. To implement the prolonged GABA response of SACs, GABA channels were not closed immediately when the moving bar shifted to the right, but stayed open for a variable time (1.2 s in Fig. 4D) before closing. In Fig. 4D, the intracellular Cl⁻ gradient was simulated as in Fig. 4C. The resultant calculated response of the SAC cell body was generally similar to our experimental data, including (1) a hyperpolarization when the bar moved centripetally through the RF surround (wave 1 in Fig. 2D), (2) a relatively fast depolarization when the bar crossed the RF centre (wave 2 in Fig. 2D), and (3) a slow depolarization when the bar moved centrifugally through the surround (wave 4 in Fig. 2D). The only noticeable difference between the experimentally recorded and simulated responses of the cell body was the absence of a fast hyperpolarizing wave in the calculated response (Fig. 4D), which separated the fast glutamate-mediated central depolarizing wave from the subsequent slow GABA-mediated depolarizing wave in the experimentally recorded response (wave 3 in Fig. 2D). As described above, this fast hyperpolarizing wave represents a glutamate-mediated Off-response, because it was only observed at the offset of light stimulation of the SAC RF centre (e.g. see Fig. 2D and F; Gavrikov et al. 2006). To avoid unnecessary complexity, we did not incorporate a mechanism to generate this glutamate-mediated, non-DS hyperpolarization into our model. As a result, this non-DS component of the SAC response to stimulus motion is not found in the simulated response of the SAC soma.

The most important result of this simulation was the robust directional selectivity produced in the SAC dendrites. The centripetal dendritic tip mostly hyperpolarized and the centrifugal dendritic tip significantly depolarized in response to the simulated moving bar (Fig. 4D), resulting in a DSI of 0.53. Thus the combination of the [Cl⁻]_i gradient along the SAC dendrite and the prolonged duration of the GABA-mediated conductance enables individual SAC dendritic branches to discriminate between centripetal and centrifugal motion, converting them into elemental directional detectors that form the basis of a system that generates directional selectivity in the retina (see Discussion).

To better understand how the delayed closing of the GABA conductance can influence SAC responses to a moving bar, we have performed simulations in which the glutamate- and GABA-mediated responses were calculated independently of each other. Figure 5 illustrates SAC responses calculated when only glutamate (Fig. 5A, which is similar to Fig. 3B) or only GABA (Fig. 5B and C) channels were considered. In the cases of the GABA-mediated responses in Fig. 5B and C there was a monotonic [Cl⁻]_i gradient in which E_GA=−37 mV in the cell body, but E_GA=−77 mV in both dendritic tips. For the simulations presented in Fig. 5B, the GABA channels were closed immediately when the trailing edge of the moving bar moved from each corresponding part of the RF. Combining Fig. 5A and B, it is easy to see that interactions between GABA and glutamate channels would produce a kind of ‘Mexican hat’ response in the SAC body similar to that shown in Fig. 4C. The responses in the dendritic tips look like mirror images for both GABA and glutamate. Since the GABA-evoked voltages are near the resting membrane potential when the maximum glutamate-induced changes in the corresponding dendritic tips occur, their interaction (i.e. GABA shunt of glutamate) produces slightly smaller depolarizing responses in both tips (28.8 mV instead of 33.2 mV in the centripetal tip and 30.5 mV instead of 34.9 mV in the centrifugal tip) than occurs when only the glutamate conductance changes.

When GABA channel closing was delayed by 1.2 s (Fig. 5C), the time during which the SAC GABA channels were affected by the moving bar was increased. GABA responses in opposite dendritic tips still closely mirrored each other, but the reflectance point of their mirror images (i.e. the time at which the increasing centripetal response (dashed line in Fig. 5C) intersected the decreasing centrifugal response (dotted line in Fig. 5C) was shifted about 0.6 s to the right.

The longer duration GABA response resulted in a shift of the GABA dynamics to the right, and as a consequence, the interactions between the glutamate- and GABA-mediated conductances produced very different effects on the membrane potentials in the centripetal and centrifugal dendritic tips evoked by stimulus motion. To illustrate this, the simple sum of the simulated motion-evoked GABA (from Fig. 5C) and glutamate (from Fig. 5A) voltages in the cell body and both dendritic tips is shown in Fig. 6A. The GABA response was negative in the centripetal dendritic tip (dashed lines) at the time that the glutamate response was maximal, so that the depolarizing effect of glutamate was reduced. In contrast, in the centrifugal dendritic tip (dotted lines) the GABA response was more positive than the resting membrane potential, so that the GABA- and glutamate-induced depolarizations added together, producing a larger depolarization.

However, the actual interactions between the glutamate and GABA conductances are more complex than just the addition of PSPs because they depend on the differences in the local glutamate and GABA equilibrium potentials along the SAC dendrites and include mutual shunting of the glutamate and GABA conductances. Figure 6B, which illustrates the actual results of our model calculations (see Fig. 4D) that take into account simultaneous changes in both the glutamate and GABA conductances, reveals a much stronger direction selectivity than occurs with just voltage summation. Comparison of Figs 5A and 6B indicates that the shunting effect of the GABA conductance on the glutamate conductance resulted in a small, but not significant, reduction of the glutamate response in the centrifugal tip (from 34.9 mV to 29.4 mV), but the combination of the shunting and hyperpolarizing effects of GABA in the centripetal tip dramatically reduced the depolarizing influence of glutamate (from 33.2 mV to 8.9 mV), producing substantial direction selectivity (DSI = 0.53). In other words, for the specific condition in which the [Cl⁻] gradient along SAC dendrites was 40 mV and GABA channel closing was delayed for 1.2 s, the above described suppressive effect of GABA on glutamate-mediated excitation was strong for the centripetal, but not the centrifugal, dendrite.

To evaluate more completely the robustness of these electrical properties in generating direction selectivity, we performed motion simulations with numerous combinations of different Cl⁻ gradients along the dendrites (from 0 to −50 mV with E_GA=−37 mV in the cell body in all cases) and delays in GABA channel closing (from 0 to 1.2 s). Figure 7 depicts in a 3-D graph the amplitude of the voltage changes (Z axis) in the centripetal (Fig. 7A) and centrifugal (Fig. 7B) dendritic tips plotted against the delay in GABA channel closing (Y axis) and ΔE_GA (X axis), which corresponds to the proximal–distal dendritic difference in E_GA (=E_Cl). Compared to the condition in which E_GA was constant (ΔE_GA= 0 mV) and there was no delay in GABA channel closing, the depolarizing response in the centripetal tip was slightly reduced when only the delay in GABA channel closing was increased and changed very little when only ΔE_GA was increased. However, the combination of these two factors dramatically reduced the size of the depolarizing response in the centripetal tip. In contrast, the depolarizing response in the centrifugal tip had virtually the same amplitude with any combination of ΔE_GA and delay in GABA channel closing. Thus, the combination of an uneven distribution of Cl⁻ along SAC dendrites and a prolonged activation of the GABA conductance creates a robust directional selectivity by dramatic suppression of the response to centripetal movement, leaving the response to centrifugal movement virtually unchanged.

Figure 7. Simulated centripetal (A) and centrifugal (B) motion-induced changes in the membrane potential (ΔV_m) of SAC dendritic tips (Z) as a function of ΔE_GA (X), the proximal–distal dendritic difference in E_GA, and the delay in GABA channel closing (Y).

A, the amplitude of the depolarizing response calculated in the centripetal dendritic tip was little affected when only the delay in GABA channel closing was increased or when only ΔE_GA was increased. However, the centripetal response was dramatically reduced when both the delay in GABA channel closing and ΔE_GA were increased. B, the amplitude of the depolarizing response calculated in the centrifugal dendritic tip was not altered by increasing the delay in GABA channel closing and/or the size of ΔE_GA. ΔV_m is the response relative to the resting membrane potential.

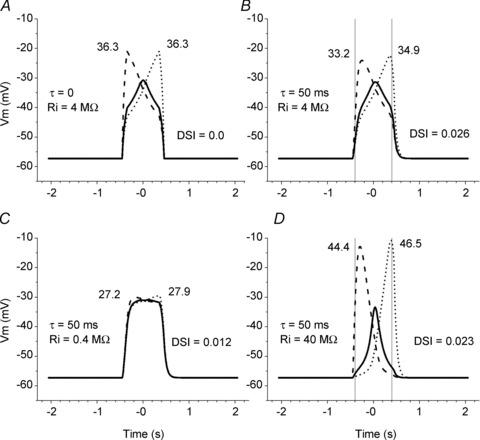
The finding that the extent of SAC direction selectivity depends on both the magnitude of ΔE_GA and the duration of the GABA-evoked increase in Cl⁻ conductance is shown graphically in Fig. 8. When E_GA was constant (ΔE_GA= 0 mV), the DSI of SACs was relatively small (i.e. <0.15) regardless of the delay in GABA channel closing (bottom curve in Fig. 8A). Also, when there was no delay in GABA channel closing, the DSI of SACs was small (i.e. <0.1) regardless of the proximal–distal dendritic difference in E_GA (bottom curve in Fig. 8B). For strong direction selectivity (e.g. DSI ≥ 0.5), both a significant ΔE_GA (e.g. ≥40 mV) and a significant delay (e.g. ≥0.8 s) in GABA channel closing are required.

Figure 8. The amplitude of SAC direction selectivity depends on both GABA channel open time and the proximal–distal dendritic difference in E_GA (ΔE_GA).

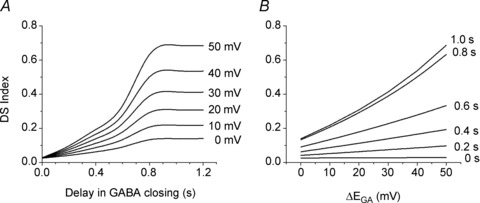
The direction selectivity index (DSI, see Results for definition) as a function of the delay in GABA channel closing at 6 different ΔE_GA (A) and the ΔE_GA (in mV) along SAC dendrites at 6 different delays in GABA channel closing (B). In both A and B, the DSI was small (i.e. <0.2) if either the GABA channel open time was short (<0.2 s) or the ΔE_Cl was small (<10 mV). In contrast, the DSI was large (i.e. ≥0.5) only when there was both a long delay in GABA channel closing (e.g. ≥ 0.8 s) and a large ΔE_GA (e.g. ≥40 mV).

Discussion

A fundamental idea that has been appreciated for decades is that a system that generates direction selectivity has to possess at least one spatial asymmetry and one temporal asymmetry (Barlow & Levick, 1965). Although a variety of spatial and temporal asymmetries may contribute to the direction selectivity of SACs (see below), our computational analysis of the DS light responses of SACs, using electrophysiological and anatomical data (Fig. 2 here; Gavrikov et al. 2003, 2006), strongly suggests that a specific spatial asymmetry (i.e. E_Cl is more positive in the proximal dendrite and more negative in the distal dendrite than the resting membrane potential) and a specific temporal asymmetry (i.e. the GABA-evoked Cl⁻ conductance lasts longer than the glutamate-evoked cation conductance) together produce most of the robust DS responses to motion in the starburst cell body and dendrites. Moreover, our analysis suggests that robust direction selectivity is produced if these two asymmetries govern both the interactions between the GABA input from the RF surround and the glutamate input from the RF centre. Although each type of asymmetry is required for direction selectivity, neither type alone is sufficient; rather, it is the combination of these two specific spatial and temporal asymmetries that generates the robust DS responses of SACs. These findings, as well as their implications with respect to the directionality of DS ganglion cells, are discussed in more detail below.

Spatial and temporal asymmetries that generate the DS responses of SACs

Minimal DS responses when only glutamate input is present

Although the GABA-associated asymmetries described above generate most of the robust DS response of SACs, a number of other spatial and temporal asymmetries, which would be present if SACs only received glutamate input, also contribute a small portion of the direction selectivity of SACs. As discussed previously (Vaney, 1990), SACs possess a spatial (morphological) asymmetry, because although synaptic inputs arrive along the length of their dendrites, their synaptic outputs are localized to the distal portions of their dendrites (Famiglietti, 1991). Due to this morphological asymmetry, the responses at opposite sides of the SAC dendritic tree may be mirror images of each other, but not the same. However, the spatial asymmetry has to be combined with a temporal asymmetry to generate direction selectivity. One source of temporal asymmetry could be the electrical capacitance of the SAC plasma membrane, which slows changes in the electrical potential. When the membrane capacitance was ignored, i.e. our modelled SAC was temporally symmetrical, the voltage response in the left dendritic tip to centripetal movement was the mirror image of the response in the right dendritic tip to centrifugal movement, and both responses had the same amplitude (see Fig. 3A). The presence of membrane capacitance slightly slowed the time course of SAC responses and decreased their amplitudes (see Fig. 3B). The capacitance-related effect was stronger for the voltage response in the centrifugal, compared to the centripetal dendrite, as the voltage in the centripetal dendrite rose promptly to its maximum value (V_cpt) when the moving bar reached the edge of the SAC dendritic tree, while the voltage in the centrifugal dendrite rose more slowly to reach its maximum value (V_cfg) because it took more time for the bar to reach the opposite edge. As a result, slight direction selectivity is present even when glutamate is the only input to the SAC. The geometry of the SAC dendritic tree can additionally enhance the DS response of the SAC dendritic tips, because SACs with branching dendrites are able to generate responses with a larger DSI (up to 0.15) than SACs whose dendrites are not branched (Tukker et al. 2004).

GABA input contributes most of the direction selectivity of SACs

Although SACs produce a slight DS response when they only receive glutamate input, experimental data show that SACs can generate much stronger direction selectivity when GABA-mediated inputs are also involved (Gavrikov et al. 2003, 2006; Lee & Zhou, 2006). Our computational analysis has shown that two specific asymmetries (one spatial and one temporal) that are associated with GABA channels are required. The spatial asymmetry results from the differential localization of two cation–chloride cotransporters, NKCC2 and KCC2. NKCC2 is located predominately on the membrane of the SAC soma and proximal dendrites and KCC2 is located mostly on the membrane of the distal dendrites (Gavrikov et al. 2006), so that the [Cl⁻] is higher than equilibrium in the proximal portion of the SAC dendritic tree, but lower than equilibrium in the distal dendrites. Consequently, GABA-evoked postsynaptic potentials are depolarizing in the proximal dendrites, but hyperpolarizing in the distal dendrites.

GABA-mediated spatial asymmetry

Our calculations predict that to generate significant direction selectivity (e.g. DSI ≥ 0.5), the difference between E_GA in the SAC soma and its dendritic tip (ΔE_GA in Figs 7 and 8) should be about 40 mV, which corresponds to an ∼4.7-fold difference in [Cl⁻]_i along the ∼200 μm length of the SAC dendrite (i.e. to a 2-fold difference in [Cl⁻]_i along an 85 μm portion of the SAC dendrite). A [Cl⁻]_i gradient along SAC dendrites of this size is quite reasonable based on two recent published experimental findings. First, experimental evidence has shown the presence of an ∼2-fold difference in the [Cl⁻]_i along the 30 μm distance between the cell body and dendrites of a retinal On-bipolar cell subtype (type 9) (Duebel et al. 2006). This experimentally measured [Cl⁻]_i gradient is almost 3 times larger than that used in the simulations shown in Figs 4, 5, 6 and 9, suggesting that the [Cl⁻]_i gradients we have simulated are indeed plausible.

Figure 9. Scheme illustrating the generation of direction selectivity in the retina.

Two ON–OFF directionally selective ganglion cells (DS GCs) with opposite directional preferences receive excitatory glutamate-gated inputs (black squares) from two ON-centre bipolar cells (BCs) and inhibitory GABA-mediated inputs (grey circles) from two dendrites, which point in opposite directions, of the same starburst amacrine cell (SAC). The voltage traces associated with each of the cells and their processes (indicated by curved arrows that point to the traces from the cells/dendrites) represent the responses evoked by a light stimulus that moves from the left to the right. The upper voltage traces are from the BCs, the middle voltage traces are from the dendritic tips of the SAC, and the lower voltage traces are from the DS GCs. Unlike the SAC dendrites and the DS GCs, the BCs respond similarly to the moving light stimulus. The scheme illustrates that the SAC dendrite that points to the right, but not the SAC dendrite that points to the left, depolarizes in response to motion from the left to the right (indicated by the arrow at the bottom of the figure) and releases GABA. Because the GABA released from the rightward pointing dendrite suppresses the excitatory effect of the BC on the DS GC on the right, a null direction response (bottom right) to stimulus motion from the left to the right is produced. In contrast, the absence of GABA release from the leftward pointing SAC dendrite when the stimulus moves from left to the right allows the BC on the left to depolarize the DS GC on the left, producing its preferred direction response (bottom left). Because the release of GABA from the two opposite-pointing SAC dendrites is reversed when a light stimulus moves from the right to the left (not shown), the DS GC on the left produces a null direction response, while the DS GC on the right produces a preferred direction response. Dotted lines indicate E_m=−40 mV, at which significant GABA release from the SAC dendritic tips can occur. See Discussion for further details.

Second, our previously published findings (Gavrikov et al. 2006) suggest that the total change in local E_Cl along the entire proximal–distal extent of SAC dendrites is at least 21 mV, and likely to be significantly more. This conclusion is based on the finding that bumetanide, a specific inhibitor of NKCC activity at a concentration of 10 μm (Russell, 2000), hyperpolarized SACs by an average of ∼17 mV, and that furosemide, a specific inhibitor of KCC2 activity at a concentration of 25 μm, depolarized SACs by an average of ∼4 mV (Gavrikov et al. 2006). These bumetanide/furosemide data suggest that NKCC and KCC2 are highly active at rest and that NKCC, which is preferentially located at SAC proximal dendrites, and KCC2, which is preferentially located at SAC distal dendritic tips (Gavrikov et al. 2006), drive the local E_Cl in opposite directions, so that the difference in local E_Cl between the most proximal and most distal portions of SAC dendrites is at least 21 mV. However, the combined 21 mV difference in SAC membrane potential following bumetanide and furosemide application would represent the actual difference in proximal–distal E_Cl if SACs only had a Cl⁻ conductance. The proximal–distal difference in E_Cl of SAC dendrites is likely to be significantly greater than 21 mV because SACs have substantial Na⁺ and K⁺ conductances (Taylor & Wassle, 1995; Cohen, 2001) in addition to a Cl⁻ conductance. When bumetanide and furosemide alter E_Cl by blocking NKCC and KCC2 activity, respectively, the Na⁺ and K⁺ conductances will reduce the size of the resultant change in membrane potential. As a result, the effects of bumetanide and furosemide on the membrane potential of SACs suggest that the total change in local E_Cl along the entire proximal–distal extent of SAC dendrites is actually substantially greater than 21 mV. For example, if the Cl⁻ conductance were half of the total SAC conductance, the total change in local E_Cl along the length of SAC dendrites would be 42 mV (i.e. 2 times 21 mV).

Previously published experimental measurements of a 10 mV difference in E_GABA between SAC proximal and distal dendritic compartments were likely to be an underestimate of the actual difference (see Gavrikov et al. 2006 for details). In these E_GABA experiments, GABA puffs were directed at the proximal dendrites and at the dendrites ∼100 μm from the soma, but not at the most distal, KCC2-containing, dendritic tips 150–200 μm from the soma, because the dendrites ∼100 μm from the soma, but not the most distal dendritic compartments were adequately space-clamped. Although one can improve the space clamp of SAC dendrites, for example, by blocking the K⁺ conductance of the dendrites with the inclusion of Cs⁺ in the patch pipette solution, such procedures are likely to compromise the physiological regulation of intracellular Cl⁻ (see below for discussion). Because KCC2 is preferentially located in the most distal portion of SAC dendrites 150–200 μm from the soma (Gavrikov et al. 2006), the 10 mV difference in E_GABA that was measured between SAC proximal dendrites and the dendrites ∼100 μm from the soma is almost certainly smaller than the actual difference in E_GABA between the most proximal and most distal dendritic compartments. In addition, it is technically challenging to puff GABA at specific dendritic sites and the 10 mV difference in E_GABA between SAC proximal dendrites and distal dendrites ∼100 μm from the soma obtained by Gavrikov et al. (2006) was likely to be an underestimate of the actual difference along this 100 μm portion of dendrite. Specifically, because the superfusate flowed from the proximal to the distal portions of the SAC dendrites that were studied (Gavrikov et al. 2006), GABA puffs at SAC proximal dendrites are likely to have reached the more distal dendrites, so that the distance between the sites of proximal and distal GABA applications was <100 μm.

Although the 10 mV difference in E_GABA that was measured between SAC proximal dendrites and the dendrites ∼100 μm from the soma (Gavrikov et al. 2006) is an underestimate of the actual difference in E_GABA along the entire proximal to distal length of SAC dendrites, it is nevertheless consistent with the larger difference in E_GABA based on the effects of furosemide and bumetanide described above. Finally, it is important to note that our whole-cell patch-clamp recording data from SACs are likely to provide an accurate measure of the electrical characteristics and light response properties of in vivo SACs, because SACs exhibited similar dark resting membrane potentials and responses to moving slit stimuli when recorded with patch-clamp electrodes in the whole-cell configuration and with intracellular sharp microelectrodes (Gavrikov et al. 2006), a means of monitoring neurons that does not significantly alter their intracellular milieu.

GABA-mediated temporal asymmetry

It is noteworthy that an important function of GABA-mediated responses is that they modulate glutamate-mediated responses. Our calculations show that the depolarizing effect of glutamate can vary considerably depending on whether it is associated with the GABA-evoked hyperpolarization in the distal SAC dendritic tree or with the GABA-evoked depolarization in the proximal dendritic tree (Figs 5–8). Our computational analysis of direction selectivity also suggests that an important aspect of this interplay between the GABA and glutamate inputs is that the GABA-mediated responses of SAC dendrites last longer than the glutamate-mediated responses, a modelling result that is consistent with experimental data. For example, rabbit SAC recordings show that (1) GABA-mediated responses to light stimulation of the RF surround last more than 0.5 s longer than glutamate-mediated responses to light stimulation of the RF centre (compare Fig. 2B and C here; also see Fig. 8C2 in Zheng et al. 2004 and Fig. 2A in Lee & Zhou, 2006), (2) GABA-mediated SAC to SAC synaptic signals last for more than 0.5 s following termination of the depolarization that initiated the signals (see Fig. 8C1 in Zheng et al. 2004 and Fig. 1B and C in Lee & Zhou, 2006), and (3) when synaptic transmission is blocked, SACs respond to GABA puffs at least 1.0 s longer than to glutamate puffs (see Fig. 2A here). In addition, the inhibitory component of the DS light response of rabbit On–Off DS ganglion cells has been reported to last 0.5–1.0 s longer than the excitatory component (Amthor & Grzywacz, 1993), a phenomenon that may reflect in part the long duration of the GABA response of SACs.

This temporal difference or asymmetry in the SAC response to GABA and glutamate, in which SACs respond longer to GABA than to glutamate, can be attributed to a combination of several factors. First, the stoichiometry of glutamate and GABA transporters suggests that under similar physiological conditions (i.e. similar membrane potential and neurotransmitter and ionic transmembrane gradients), glutamate transporters use a significantly stronger driving force than GABA transporters to clear neurotransmitter from the extracellular space (Richerson & Wu, 2003; Allen et al. 2004). Consequently, glutamate transporters should take up glutamate at a faster rate than GABA transporters take up GABA. Second, the higher GABA affinity and reduced desensitization of the δ-subunit-containing GABA_A receptors (Semyanov et al. 2004; Glykys & Mody, 2007), which are located on SAC dendrites (Brandstatter et al. 1995), compared to the glutamate affinity and rate of desensitization of the glutamate receptors expressed by SACs, could prolong the response of SACs to GABA compared to glutamate. Third, the release of GABA from cells presynaptic to SACs may last longer than the release of glutamate from bipolar cells.

Although the difference in the responses of dendritic tips on opposite sides of SACs to stimulus movement in one direction indicates that the dendritic branches are functionally independent, this functional independence does not require that the dendrites are electrically isolated from each other. Electrical isolation of one dendritic branch from another is only possible if both are electrically isolated from the soma. However, if the soma were electrically isolated from the dendrites, it would be impossible to record any voltage changes using a microelectrode placed in the soma. Therefore, the many published electrical recordings of starburst cell bodies (e.g. Taylor & Wassle, 1995; Peters & Masland, 1996; Fried et al. 2005; Gavrikov et al. 2006; Lee & Zhou, 2006) unambiguously indicate that SAC dendrites are not electrically isolated from the soma. On the other hand, an electrical connection between dendritic compartments does not necessitate that different parts of the cell experience the same voltage changes. The results of our computational analysis (see Figs 3–5), for instance, clearly illustrate this, because the voltage changes in the SAC soma and the centripetal and centrifugal dendritic tips were not the same, even when an unrealistically strong electrical connection between the dendritic compartments was used (Fig. 3C). In fact, the strength of the electrical connection between the different parts of a SAC could play a very important role in direction selectivity. An electrical connection that is too strong will reduce the difference in the responses generated in different cell compartments, but an electrical connection that is too weak will reduce mutual effects of different cell compartments on each other. In their computational analysis, Tukker et al. (2004) also came to the conclusion that SAC direction selectivity depends on the strength of the electrical connection between starburst dendritic compartments, such that an optimal electrical connection enhances direction selectivity.

Comparison to other experimental results and models of SAC direction selectivity

A number of quantitative and qualitative models of SAC direction selectivity which have been published during the past two decades (i.e. Borg-Graham & Grzywacz, 1992; Gavrikov et al. 2003, 2006; Tukker et al. 2004; Poznanski, 2005; Lee & Zhou, 2006; Munch & Werblin, 2006; Hausselt et al. 2007; Enciso et al. 2010) focused their analyses on different SAC properties. However, generally speaking, each of these models can be placed into one of two groups. The first (Tukker et al. 2004; Hausselt et al. 2007) utilized the experimental observation of excitatory glutamate input from bipolar cells in the SAC RF centre (Taylor & Wassle, 1995; Peters & Masland, 1996; Gavrikov et al. 2003, 2006; Fried et al. 2005; Lee & Zhou, 2006; Oesch & Taylor, 2010). These computational analyses have suggested that, in the presence of excitatory glutamate input, and with no GABA input, the addition of realistic SAC morphology and/or voltage-gated non-linearities can produce moderate SAC direction selectivity (Tukker et al. 2004; Hausselt et al. 2007).

The second group of models (Borg-Graham & Grzywacz, 1992; Gavrikov et al. 2003, 2006; Poznanski, 2005; Lee & Zhou, 2006; Munch & Werblin, 2006; Enciso et al. 2010) utilized the experimental observation that SACs receive both lateral GABA input from the RF surround and excitatory glutamate input from the RF centre (Taylor & Wassle, 1995; Peters & Masland, 1996; Gavrikov et al. 2006; Lee & Zhou, 2006). As has been previously reported (Borg-Graham & Grzywacz, 1992), our analysis found that glutamate input together with GABA shunting inhibition (i.e. GABA does not evoke a hyperpolarization or a depolarization) produced a small amplitude direction selectivity. Although a recent computational model of SACs found that direction selectivity is slightly strengthened by the differential distribution of NKCC and KCC2 along SAC dendrites and the presence of long-lasting GABA responses (Enciso et al. 2010), this analysis used a limited lateral GABA input from the RF surround and a model of SAC dendrites, in which each dendrite was composed of only two compartments, one proximal and one distal, resulting in a simulated starburst soma response to motion that did not correspond well with those that have been experimentally measured (Gavrikov et al. 2006; Lee & Zhou, 2006). In contrast, the simulations presented here utilized a GABA input that was 3-fold larger in lateral extent than the glutamate input and a biophysically realistic model of SAC dendrites in which each dendrite was divided into 100 segments or compartments that each contained transmembrane resistances and batteries (see Methods). Analysis of this computational model, which produced a simulated starburst soma response to motion that was similar to that which has been experimentally measured (Gavrikov et al. 2006), suggests that SACs will generate robust (DSI ≥ 0.5) DS light responses when, in combination with glutamate input, specific synaptic and subcellular mechanisms are present, namely (1) an NKCC2/KCC2-mediated gradient in E_Cl along SAC dendrites, so that GABA_A receptor activation hyperpolarizes SAC distal dendrites and depolarizes SAC proximal dendrites and (2) long-lasting SAC responses to GABA. In other words, the combination of these two specific GABA-associated spatial and temporal asymmetries, in conjunction with symmetric glutamate excitation, significantly enhances SAC direction selectivity.

Although we have consistently observed that displaced SACs produce robust, opposite polarity DS responses to stimulus motion through the RF surround (Fig. 2D and E; Gavrikov et al. 2006), other electrophysiological studies of SACs have resulted in diverse observations with respect to the presence/absence and characteristics of SAC DS light responses. For example, some previously published papers have reported that SACs do not produce DS light responses to stimulus motion (e.g. Peters & Masland, 1996), while others have reported a lack of GABA input to SACs (e.g. Euler et al. 2002; Fried et al. 2005; Hausselt et al. 2007; Oesch & Taylor, 2010), in spite of the presence of GABA_A receptors on SAC dendrites (Brandstatter et al. 1995; Zhou & Fain, 1995) and GABA-mediated SAC to SAC signalling (Lee & Zhou, 2006). Because SACs produce GABA-mediated DS responses to stimulus motion through the RF surround, but not to stimulus motion through the RF centre (Fig. 2D and E; Gavrikov et al. 2006; Lee & Zhou, 2006), it seems possible that the failure to observe DS light responses and/or GABA input to SACs resulted in part from insufficient light stimulation of the RF surround. In addition, although it is difficult to know with certainty, it also seems possible that the in vitro electrophysiological recording conditions play a significant role in the characteristics of the SAC DS light responses that are observed. That is, robust opposite polarity, GABA and Cl⁻cotransporter mediated, SAC DS light responses may not be observed if patch-clamp, whole-cell SAC recordings are performed under conditions that compromise the physiological regulation of intracellular Cl⁻ in mammals (e.g. low [Cl⁻] in the recording pipettes; room temperature superfusate; Cs⁺-containing or methylsulfonate-containing pipette solution).

Role of SACs in the generation of directional selectivity in the retina

We have evaluated mechanisms of dendritic computation to determine how individual SAC dendrites release the neurotransmitter GABA in a DS manner by depolarizing when light stimuli move centrifugally, but not when stimuli move centripetally. The scheme in Fig. 9 illustrates how SAC dendritic directional detectors are integrated into the retinal On-pathway network that provides directionally selective input to DS ganglion cells. In the scheme, which is consistent with the literature and incorporates the results of our calculations here, a displaced SAC with leftward- and rightward-pointing dendrites makes GABAergic synaptic contact with two different DS ganglion cells (Fried et al. 2002, Gavrikov et al. 2003). Each DS ganglion cell also receives non-directional, depolarizing input from ON-centre bipolar cells whenever the photoreceptors with which the bipolar cells are synaptically connected are illuminated. The upper two voltage traces in Fig. 9 represent the non-DS light responses of the bipolar cells. The same photoreceptors, which are located in the RF centre of the SAC, will stimulate the SAC by means of the bipolar cells. Other photoreceptor cells, which are located in the RF surround of the SAC, will stimulate the SAC by means of other bipolar and amacrine cells (not shown). The SAC light responses to the moving stimulus will be different in its left and right dendrites, as shown in the middle two voltage traces in Fig. 9, which were taken from Fig. 4D. Stimulus movement from left to right (as shown in Fig. 9) represents centripetal motion for the leftward-pointing SAC dendrite. As our calculations show, during centripetal motion, the SAC dendrite hyperpolarizes well below the level (e.g. −40 mV; indicated with a dotted line above the SAC responses in Fig. 9) that is necessary for GABA release. The hyperpolarizing effect of centripetal stimulus motion will thus prevent GABA release from the left dendrite. Glutamate input from the bipolar cell on the left therefore excites and depolarizes the DS ganglion cell on the left due to the absence of GABA inhibition, producing the preferred direction response from the DS ganglion cell on the left (lower left voltage trace in Fig. 9).

The same stimulus movement from left to right represents centrifugal motion for the rightward-pointing SAC dendrite. As shown in Fig. 4D and in the right middle voltage trace in Fig. 9, this dendrite also initially hyperpolarizes, but then depolarizes well above −40 mV, causing the release of GABA onto the DS ganglion cell on the right, coincident with the release of glutamate from the bipolar cell on the right. GABA released from the SAC dendrite on the right thus suppresses the excitatory effect of the bipolar cell on the DS ganglion cell, producing the null direction response from the DS ganglion cell, as shown in the lower right voltage trace in Fig. 9.

If a light stimulus moves in the opposite direction (i.e. from right to left), the right SAC dendrite would generate the hyperpolarizing centripetal response that does not evoke GABA release and the left SAC dendrite would generate the depolarizing centrifugal response that produces GABA release. As a result, the DS GC on the right would respond with a burst of spikes, while the DS ganglion cell on the left would be prevented from spike generation. Thus, the two dendritic branches of the same SAC, which point in opposite directions, provide a mechanism in which movement to the right is encoded as the preferred direction of the DS GC on the left and movement to the left is encoded as the preferred direction of the DS GC on the right. Of course, each SAC has many dendritic directional detectors that each represents a vector of inhibition pointing from the soma to the synaptic terminal. Because the total number of SACs is at least 10 times greater than that of DS ganglion cells, each DS ganglion cell has hundreds of SAC directional detectors from which to sample directional information. How On–Off DS ganglion cells primarily sample SAC dendritic directional detectors with similar directional vectors in both the On- and Off-sublaminae of the inner plexiform layer of the retina is still unclear.

Glossary

Abbreviations

DS

directionally selective

DSI

direction selectivity index

KCC

K⁺–Cl⁻ cotransporter

NKCC

Na⁺–K⁺–2Cl⁻ cotransporter

PSP

postsynaptic potential;

RF

receptive field

SAC

starburst amacrine cell

V_cpt

the maximum voltage change in the centripetal dendritic tip

V_cfg

the maximum voltage change in the centrifugal dendritic tip

Author contributions

A.D.: conception and design of the experiments; collection, analysis and interpretation of data; drafting the article and revising it critically for intellectual content. K.G.: design of the experiments, collection, analysis and interpretation of data. S.M.: conception and design of the experiments; analysis and interpretation of data; drafting the article and revising it critically for intellectual content. All of the experiments were performed at The Ohio State University College of Medicine, Columbus, OH. All authors approved the final version for publication.